Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

 

Avreste due buoni motivi per “picchiarmi”. Il primo si riferisce al metodo che vi ho consigliato di seguire per disegnare le traiettorie viste da un sistema rotante e che adesso lasceremo da parte per utilizzarne uno più rapido e facile da eseguire. Il secondo al fatto che userò di nuovo una specie di favoletta per entrare in argomento. Lo scopo è quello di dare a un gioco, apparentemente solo geometrico, un senso molto più fisico.

Abbiamo giocato con astronavi e con palline che scappano per la tangente. Siamo riusciti a descrivere le traiettorie di questi oggetti che tutto sono meno che banali e immediate. La loro curvatura ci porta subito all’esistenza di accelerazioni (e, quindi, di forze) fittizie e, in particolar modo, a quella di Coriolis. Leggendo la parte matematica (QUI) la cosa può anche non stupire, ma vogliamo arrivarci in modo intuitivo e fisico, abbandonando, provvisoriamente, la geometria pura.

Consideriamo una normale piastra, rotante con velocità costante. Il suo centro di rotazione sia O. Immaginiamo, adesso, una pallina P che si trovi per caso proprio sopra la piastra, ma che non la tocchi per niente (ossia non subisca attrito). Lei appartiene a un sistema inerziale, immobile e non si muove di un millimetro. Un punto fisso per il sistema inerziale, tranquillo e rilassato.

Mentre è lì che si gode il riposo, probabilmente meritato (con quella imprevedibile Cinematica non si sta mai fermi, accidenti!), gli si chiudono perfino gli occhi. Il pisolino, però, viene interrotto dalle voci che provengono dagli abitanti della piattaforma rotante. Guardando bene, infatti, la pallina nota che anch’essa è composta da tanti punti come lei, ma essi girano in modo impressionante. In particolare, vede che quelli più lontani dal centro compiono un percorso più lungo, in un certo intervallo di tempo,  rispetto a quelli che sono più vicini al centro, che è l’unico punto a non muoversi per niente.

Una corsa continua per rimanere sempre tutti solidali tra loro: lo devono fare assolutamente perché la piastra resti unita. Se anche un solo punto andasse per i fatti suoi, inizierebbe una reazione a catena e la piastra si sfalderebbe completamente. Ma quello che stupisce la pallina è ciò che dicono i punti che stanno su uno stesso raggio della circonferenza. Pur faticando come pochi, essi sembrano avercela con lei, povera pallina P in cerca di pace. Essi dicono: “Hai visto quella pallina aliena? Chi glielo fa fare a correre così e sempre ruotando attorno a O.  Per rimanere in quella posizione e mantenere quel moto deve subire sicuramente una forza che la attiri verso il centro. Meno male che corre come una disperata e riesce sempre a non cadere.

Lei  risponde subito: “No, no, amici miei… guardate che sono io che sto ferma, mentre voi girate come dei matti. Pensavo proprio a una forza che vi tiene legati al centro, ma che riuscite a contrastare mantenendo una velocità più o meno alta a seconda della vostra distanza da O”. “Ma tu sei pazza, noi siamo fermi e non fatichiamo per niente…”. “Ne siete proprio sicuri? Non è che sentite un qualcosa che vi spinge verso l’esterno?”. “Beh… adesso che ce lo dici, è vero… ci sentiamo sempre un po’ “sbilanciati” come dici tu…”.

A quel punto, la pallina P, molto preparata in materia, tenta di spiegare la differenza tra sistemi rotanti non inerziali e sistemi inerziali. Nei primi, quando si crede di essere fermi, si è invece soggetti a una forza apparente, quella centrifuga. Sono adesso i punti della piastra a rimanere sconvolti… finché uno non prende la parola: “Ma per noi sei tu che ruoti come una disperata e quindi anche tu dovresti sentire una forza fittizia che ti spinge verso l’esterno”. Non è facile per P spiegare la differenza tra sistemi inerziali e non inerziali e i punti della piastra continuano a non capire molto bene la situazione. In altre parole, continuano a ragionare a modo loro e il punto P cerca di riprendere sonno.

Che confusione però… perfino la signora Cinematica e la sua amica Dinamica cominciano ad avere le idee confuse e decidono di eseguire un esperimento per schiarirsi le idee.

Vogliono, perciò, complicare leggermente le cose e sentire “in diretta” cosa dicono di vedere i punti della piattaforma quando la pallina P si muove di moto rettilineo uniforme. Qualsiasi punto della piattaforma può parlare a nome di tutti gli altri: non per niente sono tutti solidali tra loro, a causa di forze veramente misteriose che abbracciano gli atomi e non solo. Inoltre, sentendosi fermi, possono chiedere aiuto a tutti i punti che vogliono.

La pallina P viene spostato in O, dove in pratica continua a stare ferma, anche se gira su se stessa. Poi viene sollevata (meno male) e torna ad appartenere al sistema inerziale fermo, esterno alla piastra.

Per i punti della piattaforma non è cambiato niente… hanno solo visto che sollevandosi leggermente ha cambiato il verso di rotazione su stessa. Comunque sembrerebbe proprio una di loro.

Tutto è pronto per l’esperimento. La pallina P, appartenente al sistema inerziale, deve percorrere la sua traiettoria verticale con velocità costante, partendo dal centro e dirigendosi verso il bordo in alto L’abbiamo rappresentata con un faccino sorridente, dato che ciò che deve fare è oltremodo semplice e, inoltre, le è stato detto di stare zitta.

La parola va invece a tre punti rossi del sistema in rotazione. Loro sono perfettamente solidali tra loro e quindi si muovono con velocità angolare costante. Come già detto, però, ciò non toglie che quelli più esterni siano obbligati a percorrere uno spazio più lungo per potere stare in fila con gli amici. Se non fosse così la piattaforma si sgretolerebbe… In Fig. 1 vediamo la configurazione iniziale.

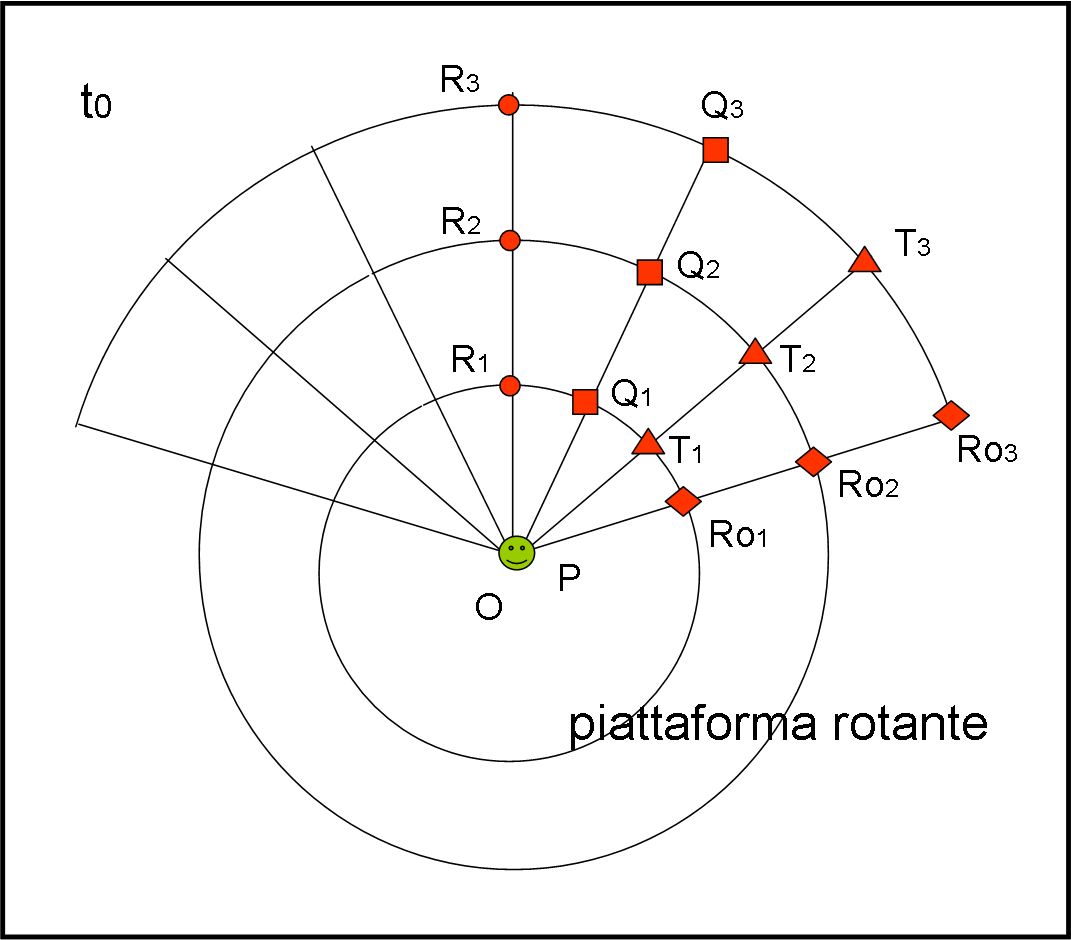
Al tempo t₀, la pallina P e i tre amici rossi (del sistema rotante), R₁, R₂ e R₃, sono perfettamente allineati. Dietro di loro, su altre tre linee solidali, vi sono gli amici quadrati (Q₁,Q₂ e Q₃) che, come quelli successivi (T₁,T₂ e T₃ e Ro₁,Ro₂ e Ro₃) serviranno per ottenere conferma delle varie posizioni raggiunte da P. I punti della piattaforma hanno studiato una bella strategia per non sbagliare nemmeno una virgola! Cinematica e Dinamica, in fondo, se ne compiacciono.

Viene dato il via a P, mentre si inizia a far ruotare la piattaforma (senza, ovviamente, dirlo ai punti rossi e ai loro amici: devono rimanere convinti di rimanere FERMI). Nel tempo Δt (sarebbe molto meglio se fosse un … dt) che la pallina impiega per arrivare al prima circonferenza, i punti rossi hanno raggiunto la seconda linea radiale verso sinistra. Siamo nelle condizioni della Fig. 2, al tempo t₁ = t₀ + Δt .

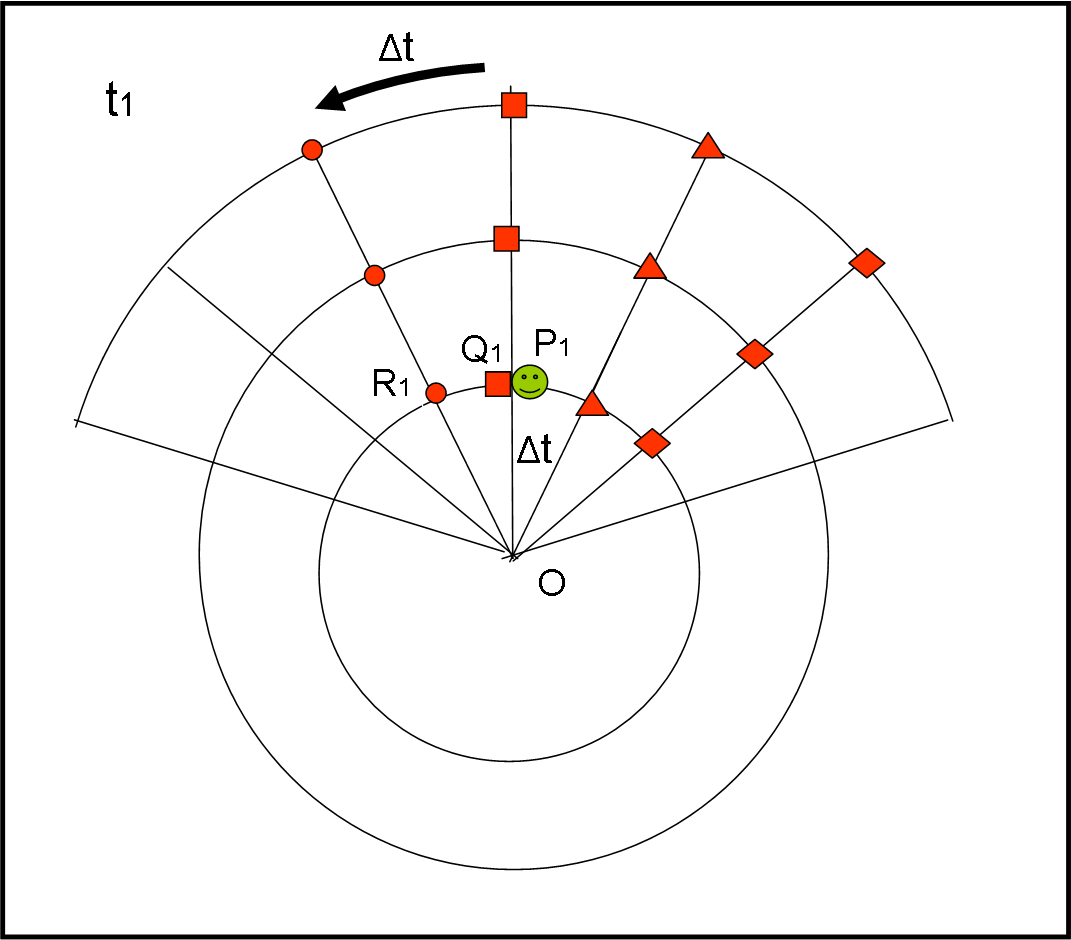
La parola va a R₁: “Ho visto chiaramente la pallina P venire verso di me in senso radiale, ma continuava anche a spostarsi verso destra di un arco di circonferenza che mi pare sia perfettamente uguale a quello che c’è tra me e l’amico quadrato.” L’amico quadrato Q₁ urla subito: “Sì, sì, hai proprio ragione. Infatti in questo istante è proprio qui dove sono io. Ma vedo che continua salire e credo anche a spostarsi verso destra”.

Passa un altro intervallo Δt e arriviamo al tempo t₂ (Fig. 3).

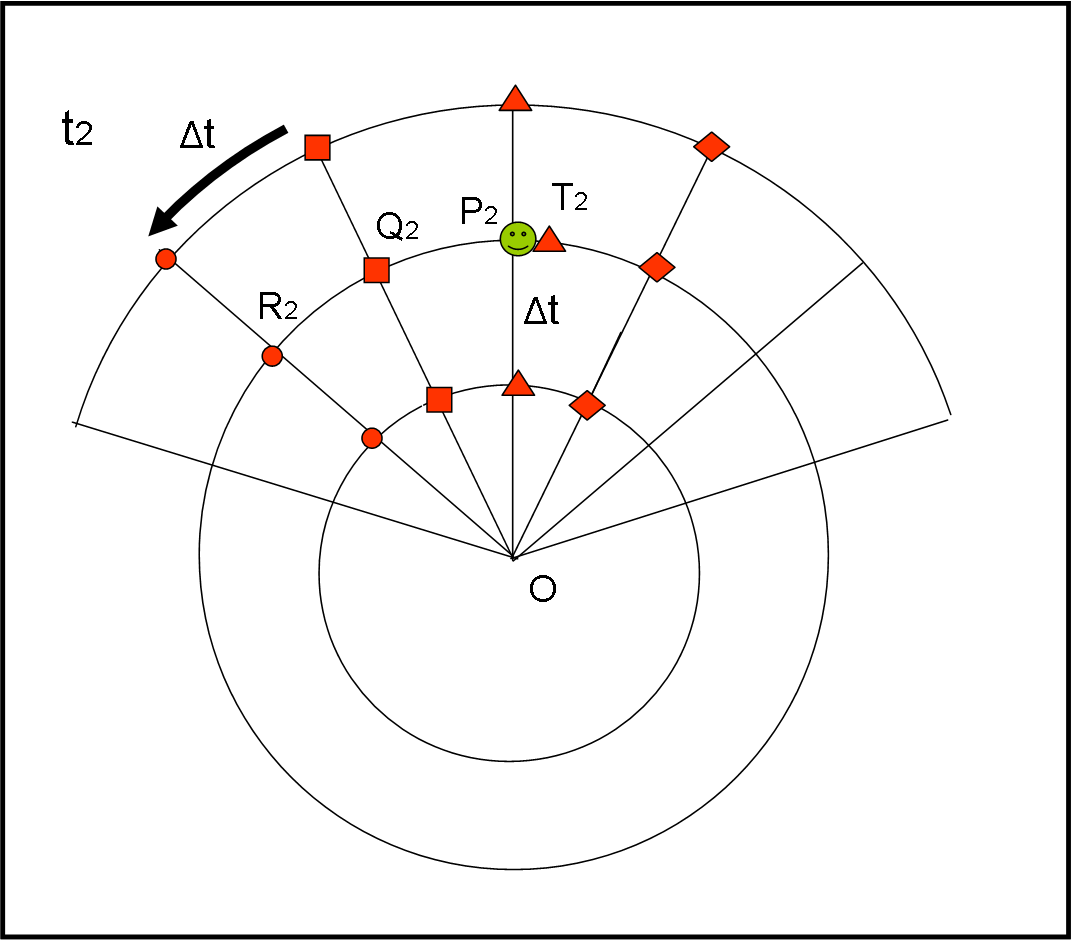
Il punto rosso R₂ prende la parola: “Ha proprio ragione Q₁… continua a salire, ma anche a spostarsi sempre di più verso destra… A me sembra che abbia percorso un tratto pari a quello che esiste tra me e Q₂. Q₂ conferma, ma chiede a T₂. Anche lui non ha dubbi: “Sì, avete ragione è proprio arrivata qui da me. Confermo lo spostamento verso l’alto e un aumento dello spostamento verso destra pari a quanto dista Q₂ da me”.

Il movimento di P continua (e la pallina continua a sorridere per come il suo movimento, così semplice, venga raccontato dai poveri punti della piattaforma), come mostrato in Fig. 4.

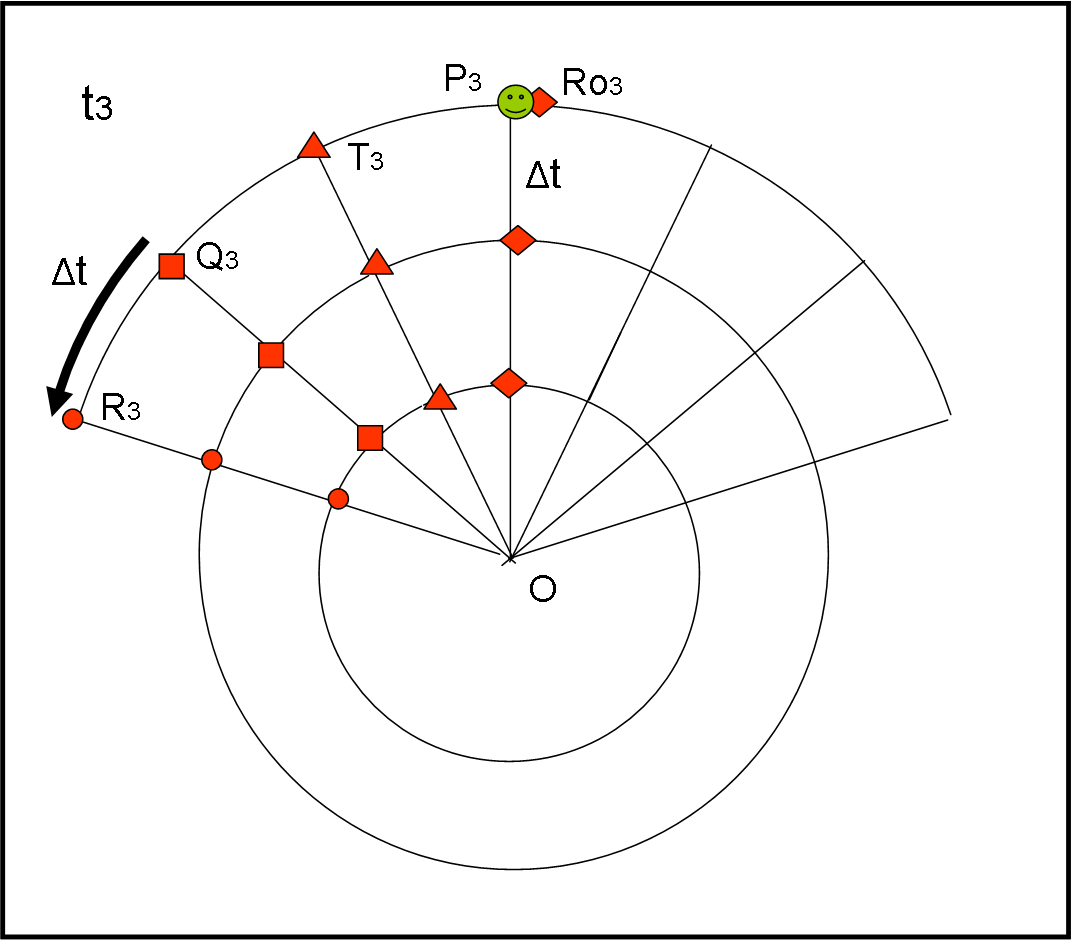
Al tempo t₃ si è portata in P₃, un movimento normalissimo. La parola va adesso a R₃: “Faccio fatica a vedere la pallina, tanto si è allontanata da me. Non vorrei sbagliare ma mi sembra che si sia spostata di ben tre volte la distanza tra me e Q₃. Q₃ conferma che l’ha visto allontanarsi verso destra, ma è meglio chiedere a T₃. “Sì, sì, l’ho vista proprio dirigersi verso Ro₃… chiediamo a lui”. “Confermo in pieno”, risponde Ro₃, “quanto detto dai miei amici e colleghi. P è proprio qui accanto a me!”.

L’esperimento si può considerare concluso e Cinematica e Dinamica vanno a segnare le posizioni di P al variare del tempo, secondo quanto detto dai punti della piattaforma. Tenendo presente che loro si sono considerati fermi, devono segnare i punti nella configurazione di partenza, ossia nella Fig. 1. Ciò che si ottiene è la Fig. 5, dove le posizioni assunte da P, secondo il sistema rotante, sono segnate in nero.

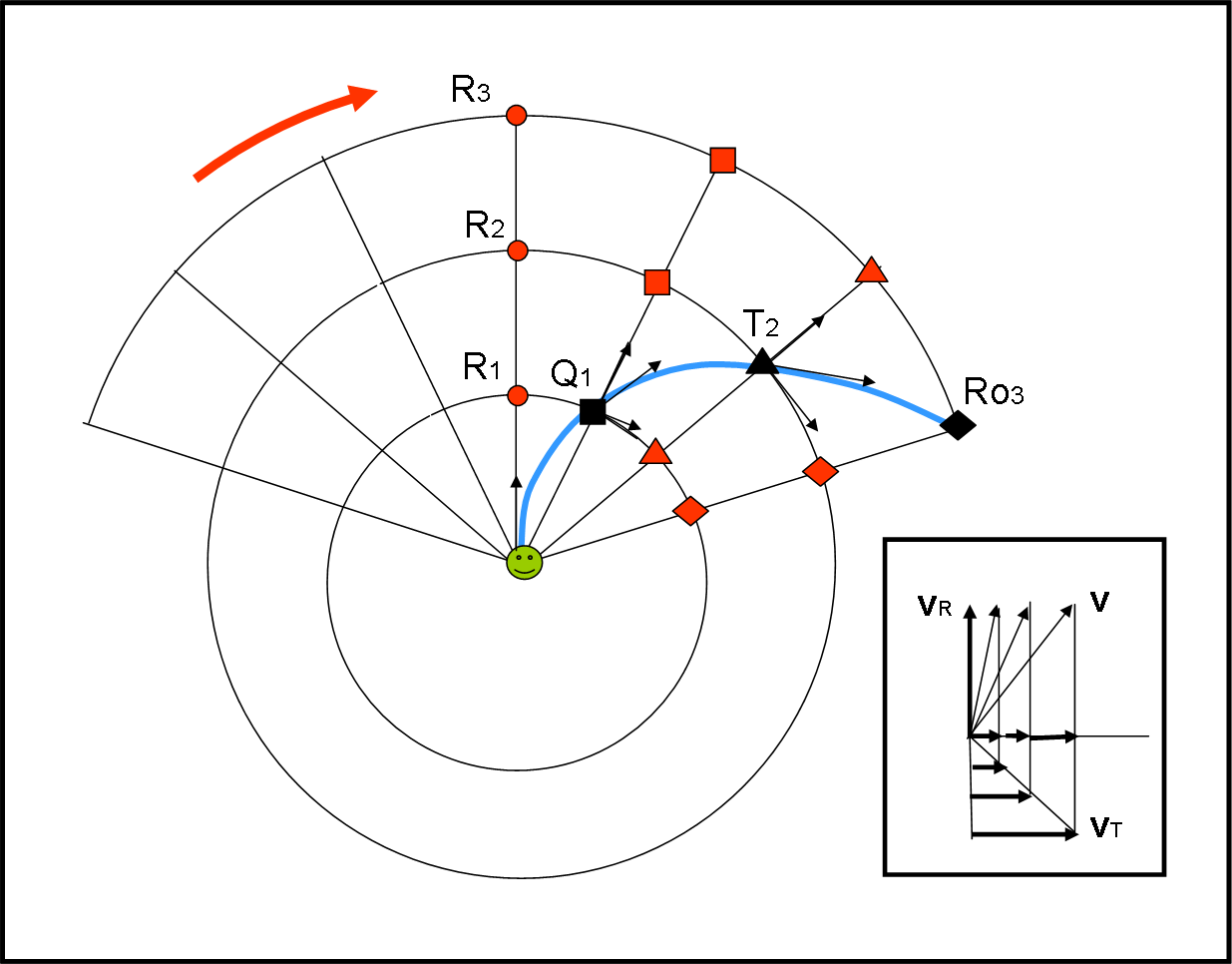
Facciamo una piccola analisi delle velocità in gioco secondo il sistema rotante. Ogni punto P ha una velocità radiale e una tangenziale (relativa alle circonferenze in cui si trovano i vari punti P secondo il sistema rotante). Mentre il modulo della velocità radiale è sempre lo stesso, cambia invece il modulo della velocità tangenziale (ci spostiamo verso l’esterno). Le velocità sono state tracciate in Fig. 5 e nel riquadro in basso a destra.

Ne nasce una strana curva che è causata da almeno due accelerazioni, che devono dare un senso fisico alla soluzione. Per arrivare ad esse bisogna notare che la velocità radiale ha modulo costante ma varia la direzione, mentre quella tangenziale varia anche in modulo. Insomma, deve comparire sia un’accelerazione centrifuga, dato che vi è un allontanamento in senso radiale, ma anche quella di Coriolis che dipende dalla velocità lungo la traiettoria. Tutto ciò può essere ottenuto partendo dalle formule ricavate QUI, manovrando sapientemente la… mano destra.

In poche parole: secondo il sistema rotante la pallina che si muove verticalmente, appare sempre “IN RITARDO” rispetto ai punti della piattaforma e, dato che loro si considerano fermi, appare spostarsi sempre di più verso l’esterno e verso destra.

Tutto questo da un punto di vista “fisico”…

Da un punto di vista geometrico e pratico (non arrabbiatevi!), risulta subito chiaro, dalla Fig. 6,  il metodo più immediato per costruire velocemente e semplicemente la curva descritta da P.

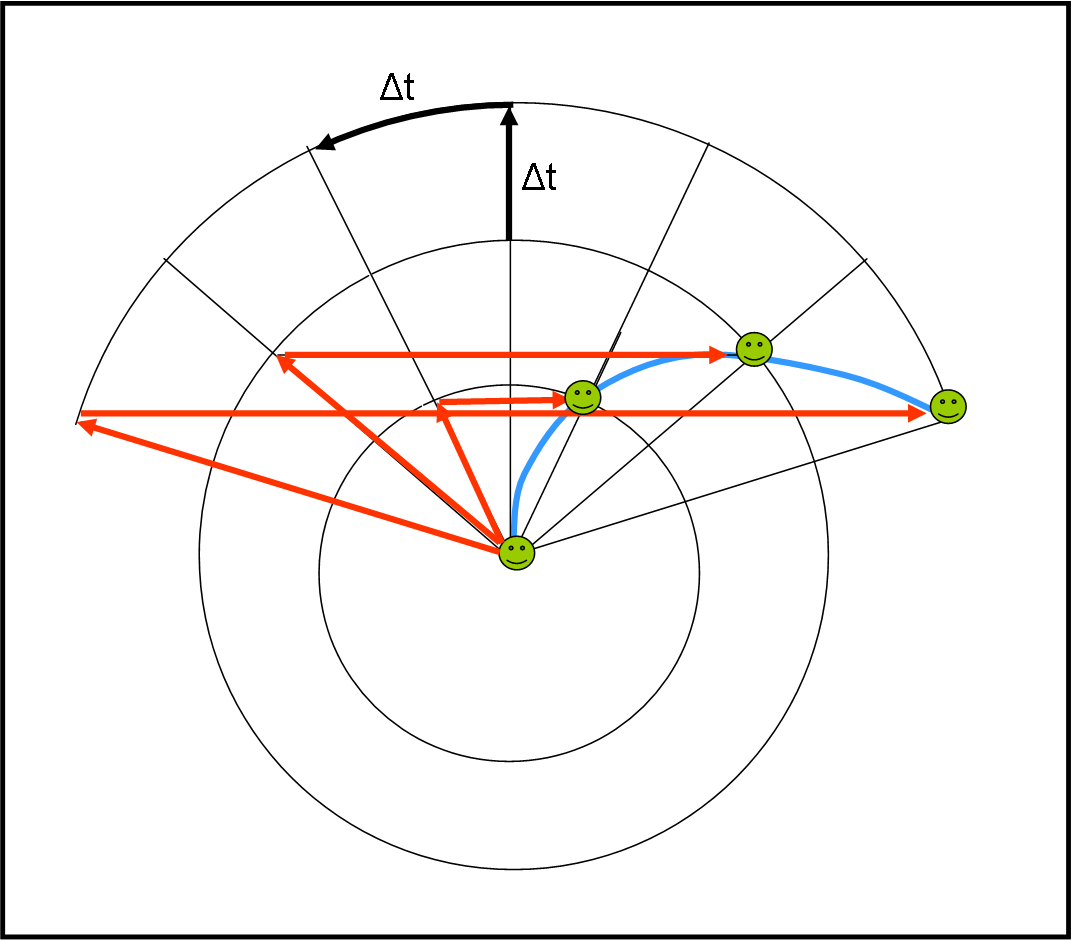
Basta tracciare i raggi, per intervalli di angolo costanti, e, quindi, anche di tempo costante (la velocità angolare è costante). Intervalli di tempo che vengono descritti anche dalla pallina per passare da una circonferenza più interna a una più esterna. Poi basta seguire le frecce rosse… banale e concettualmente più che intuitivo! Detto tra noi, non abbiamo fatto altro che usare delle coordinate polari, ben più comode, in questo contesto, rispetto a quelle cartesiane … ma sapete, sono sempre un po’ malvagio… e, poi, in fondo, quelle belle figure con i triangoli rotanti erano tanto simpatiche…

Tra parentesi, lavorando con i triangoli (cartesiani), si poteva arrivare alla soluzione più comoda e rapida di questo articolo, trafficando un poco con la geometria. Ce lo mostra la Fig. 7, dove il blu si riferisce al “vecchio” metodo e il rosso a quello “nuovo”. Non vi è bisogno di ulteriori parole…

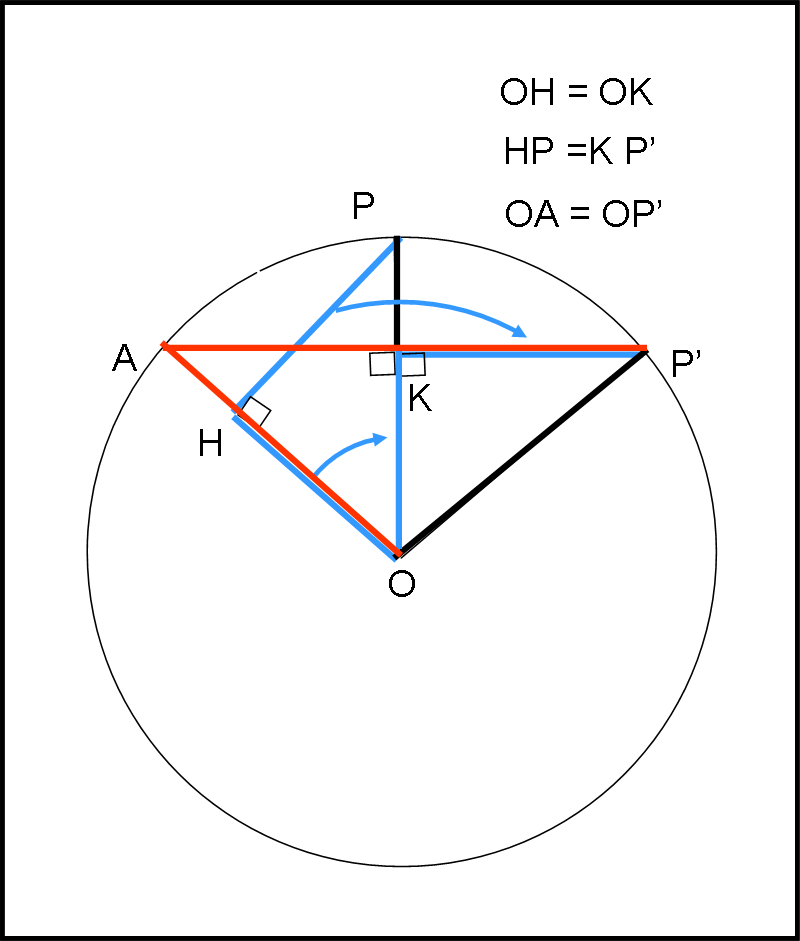
Probabilmente, molti di voi avranno fin da subito adottato il secondo metodo, ma io ho preferito eseguire i due passaggi per arrivare lentamente all’essenza fisica, partendo da una puramente geometrica. Al limite, se non la gradite, fatemelo sapere ed eseguirò le correzioni nell’articolo definitivo di approfondimento.

Fermiamoci qui e dalla prossima volta saremo molto più… rapidi.

 

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis