Categorie: Fisica classica
Tags: aerei astronavi equatore forza di Coriolis meridiano Papalla polo nord quiz
Scritto da: Vincenzo Zappalà
Commenti:7
QUIZ: la sfida aerea su Papalla ***
Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.
E’ giunta l’ora di tirare un po’ le somme, dopo aver giocato con palline e astronavi varie. Vediamo, perciò, se abbiamo capito bene ciò che succede con questi sistemi inerziali e non inerziali. In particolare, cominciamo a definire per bene cosa si vede o non si vede passando da un sistema all’altro. Avete già capito che la forza di Coriolis domina la situazione (ma non solo…). Sfruttiamo, allora, le caratteristiche del nostro pianeta amico Papalla, dove non c’è atmosfera e gli abitanti amano moltissimo le gare.
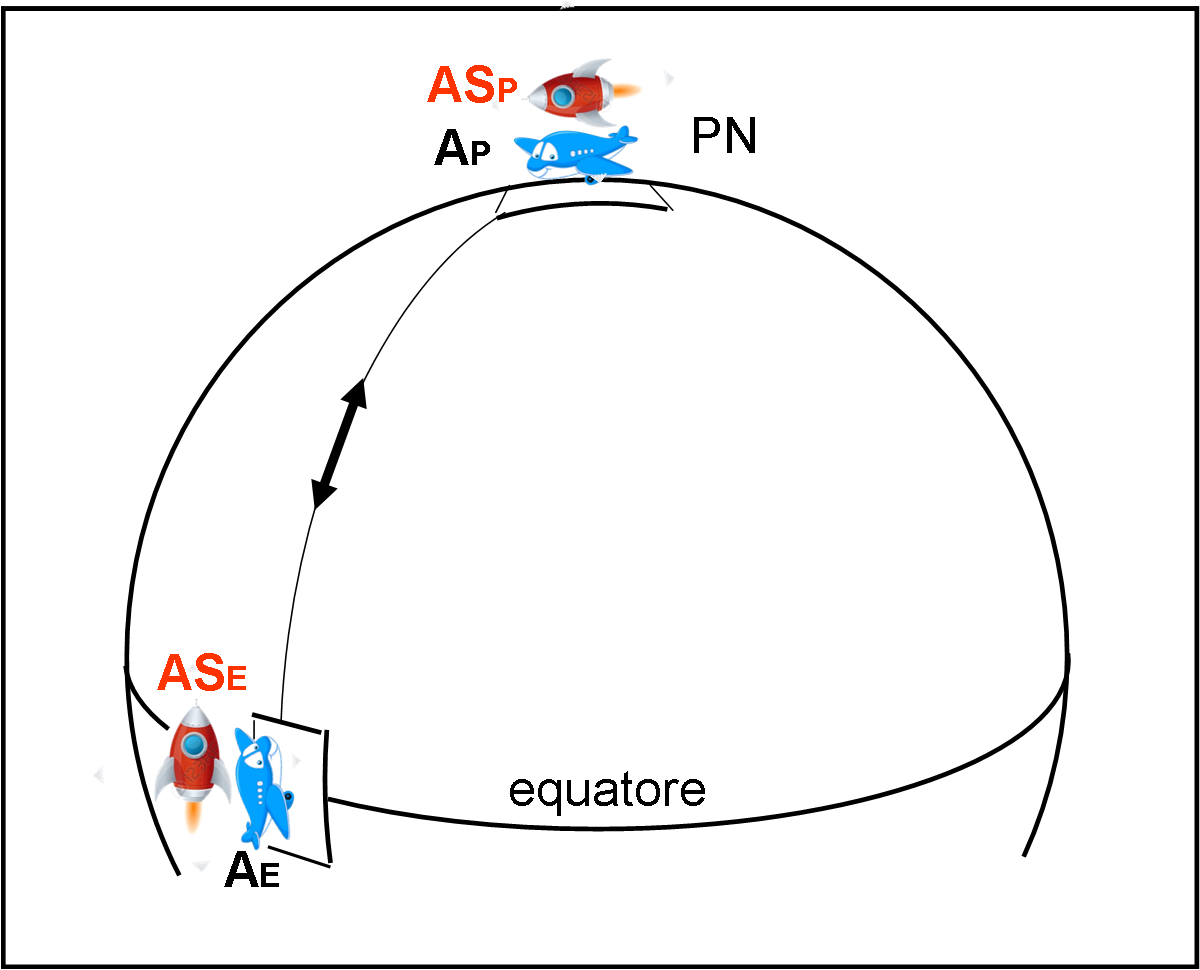
Su Papalla vi sono due grandi aeroporti, uno posto esattamente al Polo Nord e uno posto sull’Equatore. Alla gara partecipano due aerei di linea e due astronavi. Gli aerei sono parcheggiati nell’aeroporto, mentre le astronavi sono tenute in stallo sopra gli aeroporti, manovrando alcuni motori aggiuntivi (ma a noi poco importa). I due aerei sono AE e AP, mentre le due astronavi sono ASE e ASP . Lo scopo della gara è quello di raggiungere l’aeroporto opposto, ossia AP e ASP devono raggiungere l’aeroporto all’equatore e viceversa per AE e ASE.
Ricordiamo che Papalla ruota intorno al suo asse come fa la Terra (l’asse passa per il Polo Nord e il senso di rotazione è quello antiorario se visto da PN) e, come sappiamo bene, non ha atmosfera. Trascuriamo del tutto anche gli effetti della gravità.
Le condizioni della gara sono quelle della figura che segue.
I piloti ci pensano un po' sopra e poi decidono tutti di seguire la rotta apparentemente più corta, ossia quella del meridiano che passa per i due aeroporti nell'istante della partenza. Una volta stabilita la rotta non la si può più cambiare! Le astronavi fermano i motori che le tenevano in sospensione e si lanciano verso i rispettivi traguardi. I due aerei fanno lo stesso, dopo essere decollati dagli aeroporti.
Per non cadere in confusione, possiamo dire che le astronavi sono del tutto estranee al pianeta (un po’ come quella che aveva spaventato l’Italia in questo quiz).
Le domande a cui si deve rispondere sono le seguenti:
1) Quali tra i quattro velivoli raggiungeranno il traguardo?
2) Il risultato è lo stesso se viene visto da un sistema esterno inerziale o se viene visto da un osservatore solidale con Papalla?
3) Tracciare le traiettorie indicative (a mano libera) dei quattro velivoli, sia in un sistema che nell’altro.
In casi disperati (penso che, però, se letto per bene quanto scritto finora su Coriolis & co., non abbiate problemi) inserirò una figura analoga, ma più facilmente “trattabile”.
Forza… non abbiate paura. Ci possono arrivare tutti e tutti possono rispondere… (l’importante è non andare a vedere le soluzioni eventuali, già date nei commenti... i maghi e i loro amici sono terribili e veloci). Consiglio ad Arturo di non provare a fare veramente l'esperimento, come suo solito: gli costerebbe un po' caro!
P.S.: Speriamo solo che PapalScherzone, come al solito, non s’intrufoli e ci scombussoli la gara; al limite potrebbe partecipare...
QUI la soluzione
In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis






7 commenti
Tenendo conto che il Professore è sottile ma non malizioso,
Quasi quasi... l'esperimento si potrebbe pure fare, non ci vuole molto a trovare un pallone di gomma di quelli che una volta si usavano per saltarci sopra. Lo si dota di un motore (un trapano con velocità regolabile ?) per farlo ruotare sul suo asse verticale. E abbiamo Papalla (anzi, Papallone) . Il problema è : come simulo l'aereo che percorre la rotta fissa dall'equatore al polo nord ? Un drone ? Sono ancora troppo grossi, in proporzione al pallone... Diverso il discorso se si fosse parlato di fiumi....
Comunque, io in questo caso opto per il Prof malizioso, più che per quello sottile.
Temo di non essere stato compreso appieno... La rotta è decisa fin dall'inizio e la velocità è costante. Se sono al centro di una giostra che ruota e sul bordo c'è una buca da golf, riesco sempre a far entrare la pallina in buca, mirando a dove sta la buca nell'istante iniziale (ossia quando lancio la pallina?). Il succo è questo...
Aggiungo: non c'è atmosfera e quindi non c'è attrito...
caro Leandro (ma vale per tutti).
ciò che credo di aver capito abbia fatto tu è considerare l'aereo parte integrante della Terra, come se una macchina percorresse una strada che congiungesse i due aeroporti. Ma l'aereo, una volta partito, è indipendente dalla Terra (non c'è nemmeno atmosfera...). Magari, se le teste non girano troppo, potremo tornare sul tuo esempio...
Le condizioni di gara sono:
1) assenza di atmosfera e di forze di attrito;
2) trascurabilità dell’attrazione gravitazionale del pianeta;
3) percorso scelto da coprire 1/4 di un determinato meridiano;
4) non si può correggere istante per istante la rotta scelta (dv/dt = 0), ma viaggiare al disopra di essa come se fosse un binario rigido;
5) gli aerei riescono a librarsi in volo anche senza portanza.
Da un punto di vista fisico dovrebbe succedere questo:
Ae (aereo con verso Eq → PN) si trova poggiato all'equatore ed è dotato della massima velocità tangenziale relativa alla velocità di rotazione (costante) intorno all'asse papalliano ed alla distanza da esso (raggio equatoriale papalliano), ed essendo dotato di massa possiede anche un valore massimo possibile di quantità di moto iniziale (relativamente alla velocità tangenziale). Iniziando a volare dal bordo verso il PN, è soggetto all’accelerazione di Coriolis dovuta alla rotazione del pianeta (accelerazione inizialmente nulla all'equatore, via via crescente procedendo verso il PN) ma si porta sul groppone anche la massima quantità di moto iniziale, (è in anticipo nei confronti dello spostamento verso est dei punti giacenti sul meridiano di riferimento, essendo questi dotati di velocità tangenziale via via decrescente avvicinandosi al PN, e si trova sempre un po' più a est rispetto al meridiano di riferimento). Da terra (punto di vista del sistema rotante), la sua traiettoria appare curva e procede verso nord-est, fuori dal binario della rotta e, non potendo correggerla, non giungerà all’aeroporto PN, ma a est di questo. Dall’alto (punto di vista del sistema fisso), la traiettoria è rettilinea.
Ap (aereo con verso PN → EQ) si trova poggiato al PN ed è dotato della minima velocità tangenziale relativa alla velocità di rotazione (costante) intorno all'asse papalliano ed alla distanza da esso (pari a zero sul punto del PN, raggio zero), ed essendo dotato di massa possiede anche un valore minimo possibile di quantità di moto iniziale (relativamente alla velocità tangenziale, nulla sul punto del PN) . Iniziando a volare dal centro verso il bordo, è soggetto all’accelerazione di Coriolis dovuta alla rotazione del pianeta (accelerazione inizialmente massima al PN, via via decrescente procedendo verso l'EQ), deviando verso ovest rispetto al meridiano di riferimento (è in ritardo nei confronti dello spostamento verso est dei punti giacenti sul meridiano di riferimento, essendo questi dotati di velocità tangenziale via via crescente avvicinandosi all’EQ, e si trova sempre un po' più a ovest rispetto al meridiano di riferimento). Da terra (sistema rotante), la sua traiettoria appare curva e procede verso sud-ovest, fuori dal binario della rotta e, non potendo correggerla, non giungerà all’aeroporto EQ, ma ad ovest di questo. Dall’alto (punto di vista del sistema fisso), la traiettoria è rettilinea.
Le navicelle spaziali ASe e ASp non sono poggiate a terra e si comportano come la navicella aliena del quiz precedente, con la differenza che ASp parte da centro.
Dal punto di vista del sistema fisso, le traiettorie dei 4 velivoli sono rettilinee.
Ma dovrebbe giungere al “traguardo” solo la navicella spaziale che parte dal bordo (ovvero dall'equatore) (ASe).
https://i.imgur.com/ytRn8bk.jpg
caro Andy,
per adesso posso solo dire che hai fatto un gran lavoro... che sia giusto lo vedremo...