Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

 

Ecco a voi la soluzione del quiz degli aerei e delle astronavi. Devo subito dire che Andy è stato qualitativamente (quello che si richiedeva, d’altra parte) molto preciso. Grazie per il suo impegno. Mi sto accorgendo sempre di più che un  semplice moto rotatorio inneschi problematiche non proprio banali, per cui continuo a batterci sopra, puntando ai concetti piuttosto che alle formule (quelle le abbiamo già date).

Per disegnare una traiettoria percorsa in un sistema non inerziale basterebbe teoricamente ricavare le equazioni del moto. La faccenda non è però proprio immediata dato che nella formula delle accelerazioni (quelle con le derivate seconde delle coordinate dei punti) ne compaiono due fittizie, quella centrifuga e quella di Coriolis. Si potrebbero eseguire delle semplificazioni, ma preferisco portare alla soluzione per via grafica decisamente più intuitiva, completa e facilmente eseguibile da tutti.

Inoltre, aver inserito la Terra nel nostro quiz complica decisamente la faccenda. Infatti, abbiamo parlato sempre di moto a velocità costante di un  oggetto su una superficie rotante. La terra vista dal polo assomiglia molto a un disco rotante, tuttavia non lo è esattamente, in quanto se l’aereo si muove di velocità costante, s’intende che la sua velocità è misurata rispetto al suolo che è curvo. Ne consegue che la sua velocità sull’ipotetico disco rotante (la Terra proiettata sul piano equatoriale) deve essere variabile, come illustra la Fig. 1.

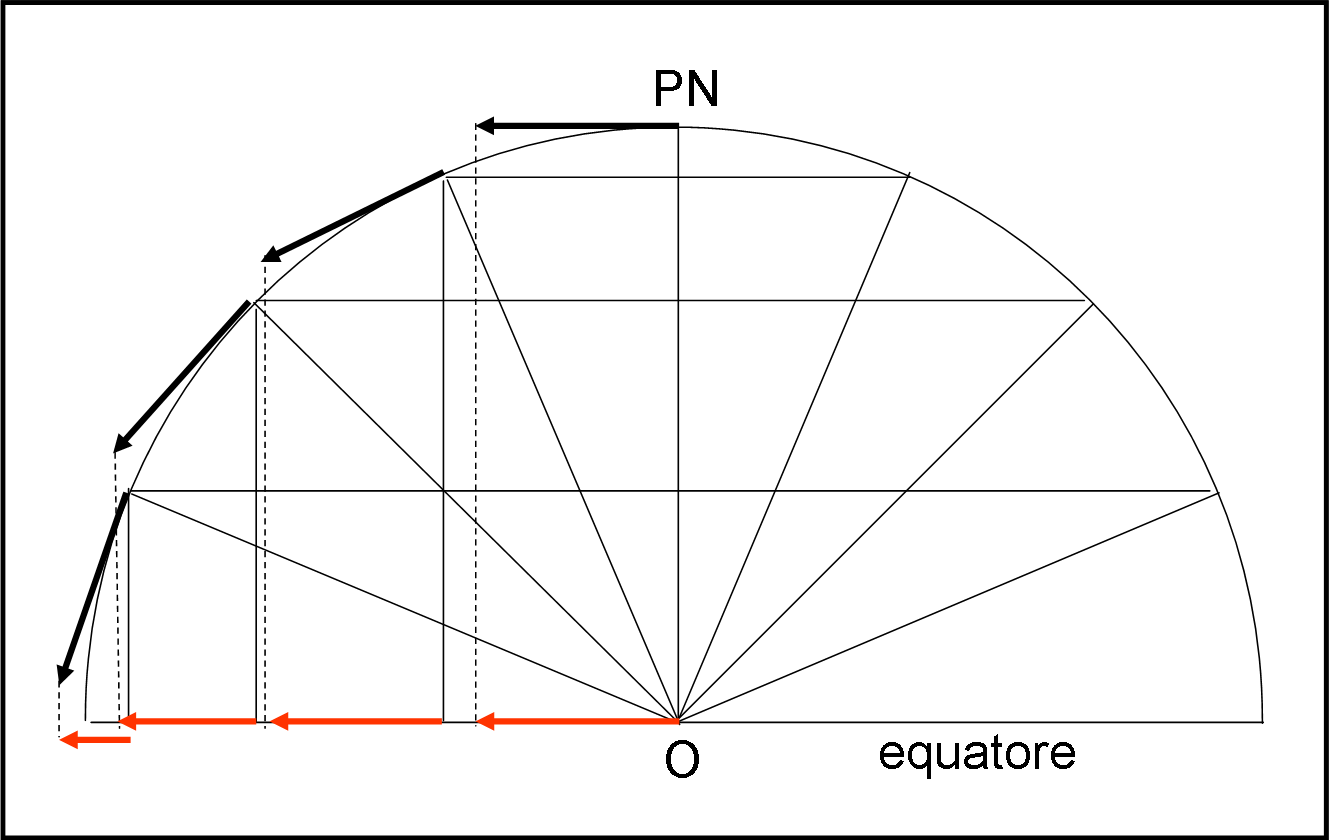
Lo stesso tratto di circonferenza comporta lunghezze, nella proiezione, decrescenti avvicinandosi ai poli e viceversa. Inoltre non consideriamo la forza di gravità che dà un suo aiuto nel muoversi variando la latitudine. Insomma, è molto meglio semplificare ancora di più il quiz (basta e avanza) e ridursi a un vero disco rotante, in cui la velocità rimanga veramente costante. Già cosi ne vedremo delle belle…

Riproponiamo, allora, il quiz traslocando il tutto su una piattaforma girevole piana (i risultati saranno praticamente gli stessi).

Cominciamo con la Fig. 2.

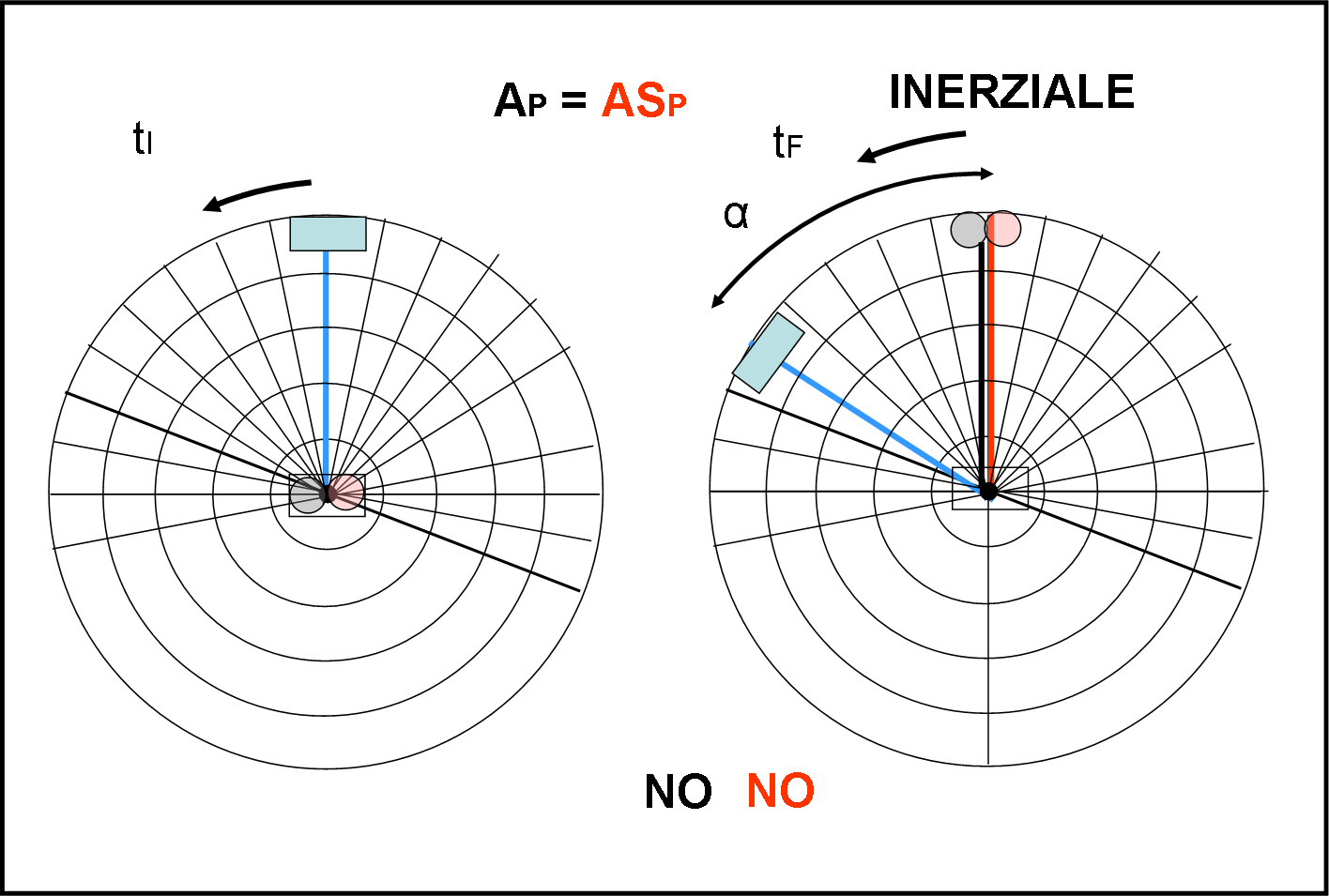
In questo caso abbiamo l’aereo e l’astronave che sono nel punto centrale e devono mirare all’aeroporto posto ai bordi della piattaforma (rettangolo celeste). Vediamo il tutto nel Sistema Inerziale. Non ci vuole molto a capire che partendo dall’origine poco importa che l’aereo appartenga al sistema inerziale e l’astronave no. L’origine è la stessa per entrambi i sistemi e quindi l’aereo e l’astronave non subiscono nessuna velocità prima della partenza: nessuno dei due ruota (ovviamente consideriamo aerei e astronavi puntiformi). Al tempo t_I essi vedono l’aeroporto davanti a loro e partono immediatamente, mantenendo una traiettoria rettilinea. Riescono a farlo benissimo, essendo svincolati dalla rotazione e non avendo velocità “residue”, solo quella di volo. Tuttavia, quando arrivano sull’equatore (bordo esterno della piattaforma), al tempo t_F, l’aeroporto non è certo stato fermo! Esso ha ruotato di un certo angolo α ed è decisamente più avanti dei due velivoli. Nessuno dei due raggiunge l’aeroporto, ma un punto spostato verso destra rispetto a lui.

In Fig. 3 riproponiamo l’esperimento, mettendoci, però, nel sistema rotante.

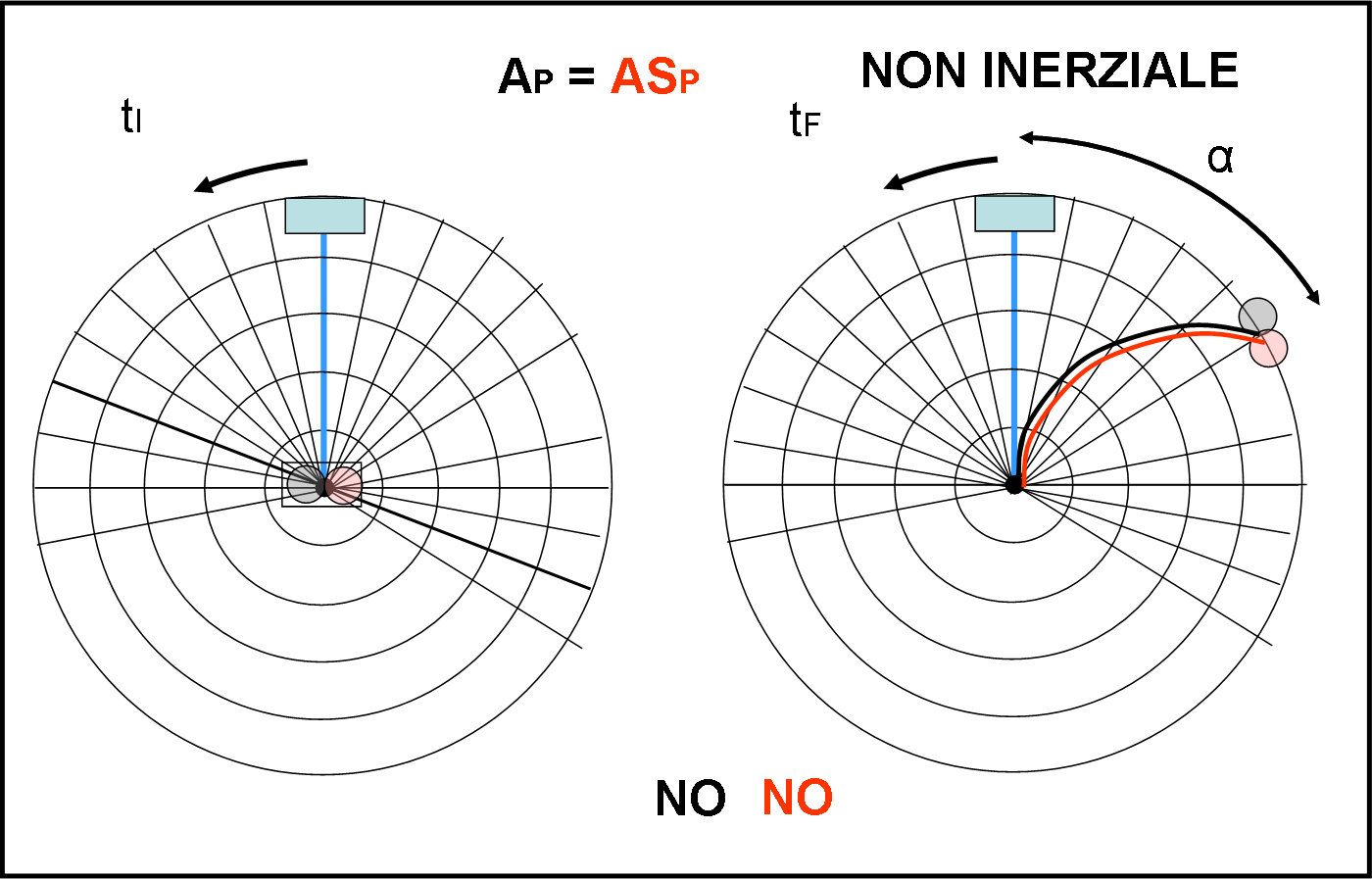
Potremmo già concludere  che niente può cambiare nell’esito finale: il fenomeno meccanico deve restare lo stesso… cambia solo il modo di spiegarlo e per far ciò si devono introdurre forze fittizie. Tuttavia, è sempre interessante studiare e descrivere la traiettoria che seguono aereo e astronave per “mancare” di molto l’aeroporto di arrivo. Beh… per costruire la traiettoria basta seguire uno dei metodi descritti nelle altre puntate relative a Coriolis e si ottengono due curve identiche, dato che le condizioni sono le stesse. Ovviamente la curva ci dice che sono all’azione sia la forza centrifuga (in senso radiale) che quella di Coriolis (perpendicolare alla traiettoria), in modo tal da far atterrare sia l’astronave che l’aereo nello stesso punto, alla stessa distanza dall’aeroporto che dovevano raggiungere. Questa distanza angolare è, ovviamente, α.

Passiamo adesso al caso in cui i velivoli partano dall’aeroporto equatoriale.

Mettiamoci nel sistema inerziale (Fig. 4).

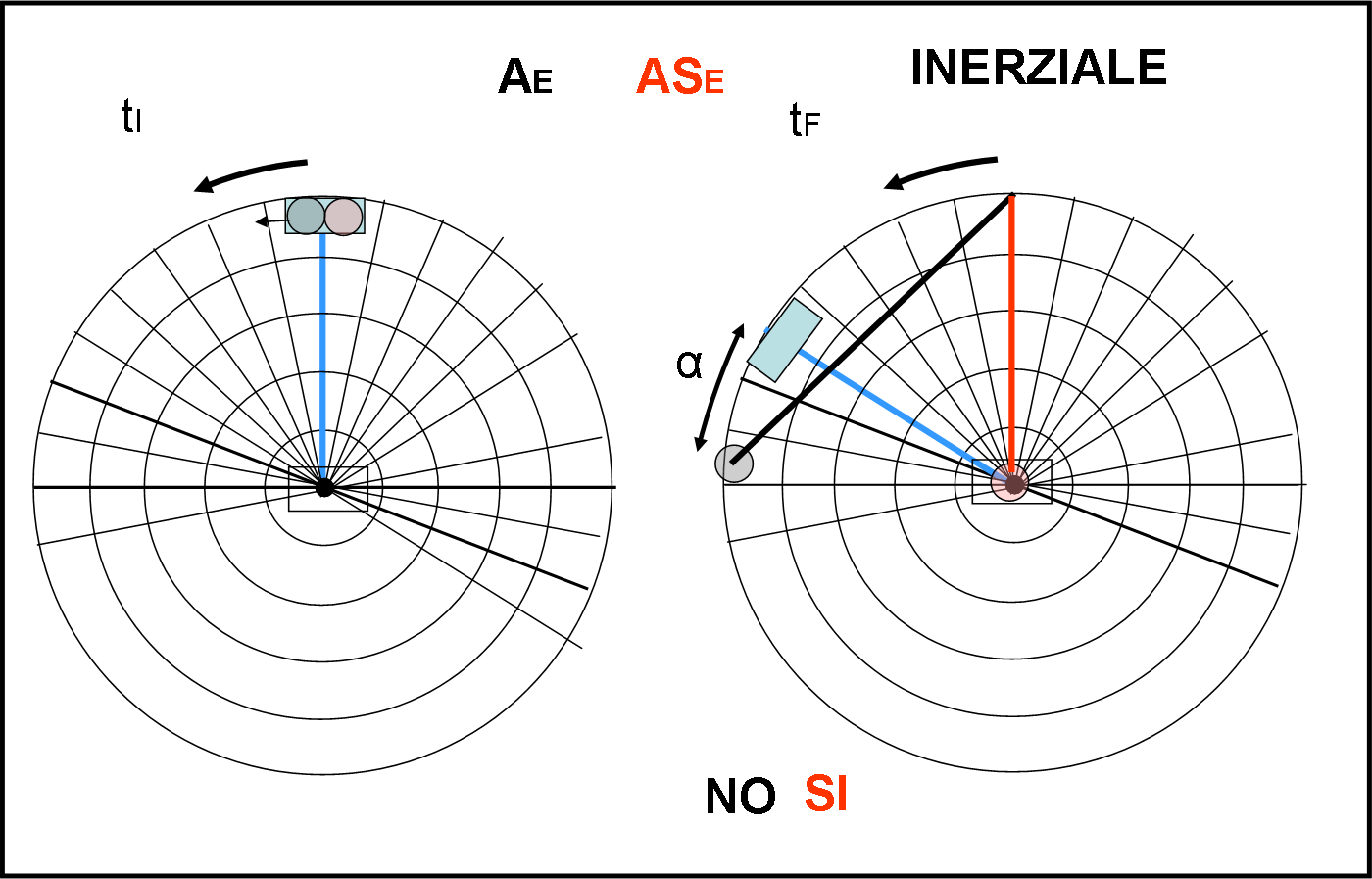
Le due traiettorie differiscono immediatamente. L’astronave vive nel sistema inerziale e quindi è FERMA nel suo sistema. L’unica velocità a cui è soggetta è quella che la fa dirigere verso l’aeroporto polare. Il centro, ossia il polo, non subisce rotazione, per cui essa non ha nessuna difficoltà a raggiungere l’aeroporto: operazione riuscita! L’aereo , invece, sta girando insieme alla piattaforma e quindi ha una sua velocità intrinseca tangenziale (moto circolare uniforme). Anche se lo poniamo al di fuori della piattaforma durante il volo, questa componente non viene cancellata (principio d’inerzia).

A questa si deve sommare la velocità diretta verso il centro. La sua traiettoria è, di conseguenza, la retta nera diretta verso destra rispetto alla rotazione. Non solo l’aereo non raggiunge il polo, ma, a momenti, torna da dove è partito! Riesce, infatti, ad anticipare, solo dell’angolo α, l’aeroporto equatoriale che sembra quasi inseguirlo… In poche parole, l’astronave riesce a raggiungere il bersaglio, mentre l’aereo sembra proprio impazzito.

Non ce ne sarebbe nemmeno bisogno, ma concludiamo guardando cosa si vede nel sistema non inerziale in Fig. 5.

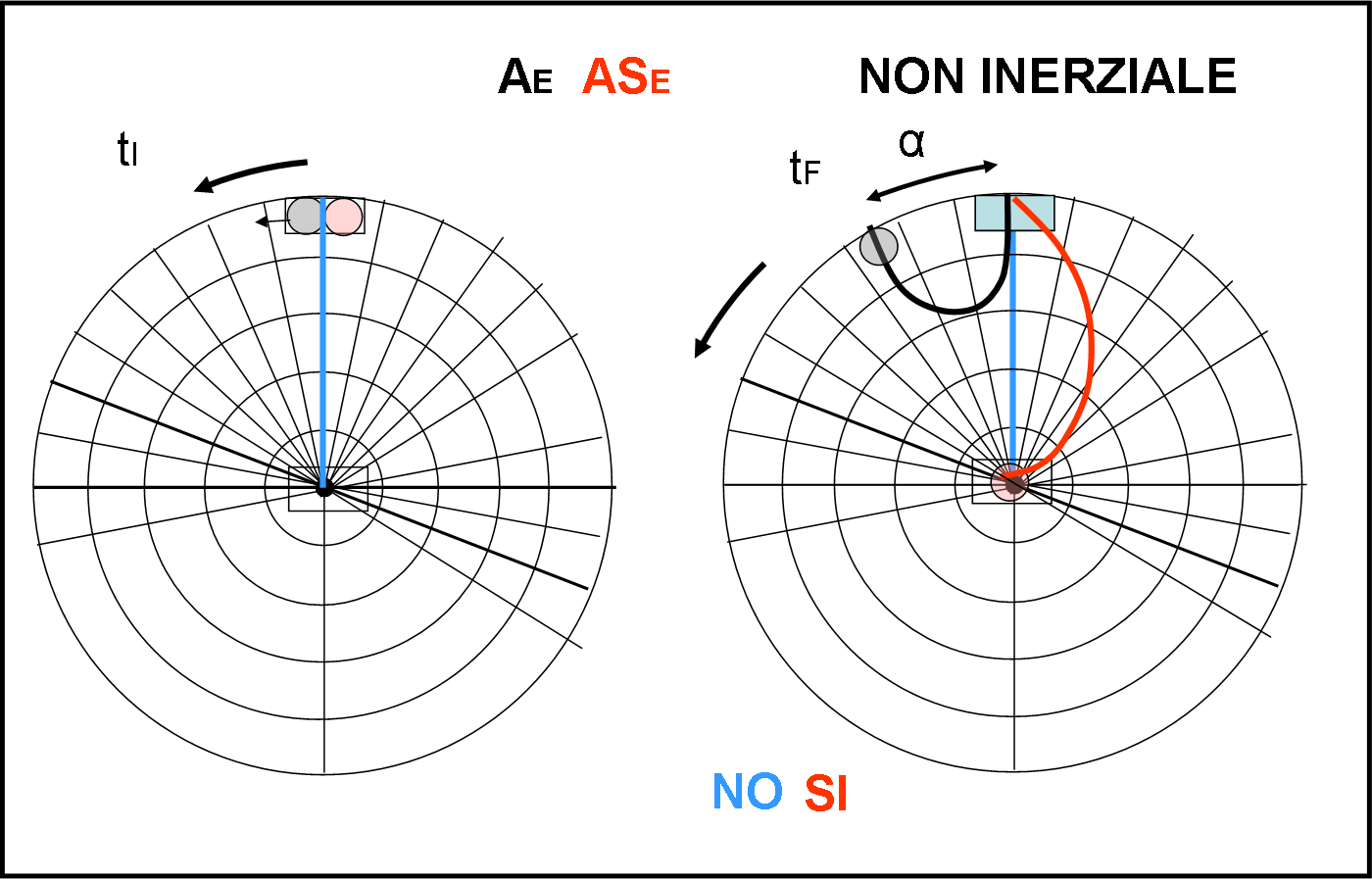
Qui devono apparire delle curve, dato che devono agire le forze fittizie. Cosa succede all’astronave? Facile a ricavarsi. Lei sembra andare verso sinistra, fa un bel giro, ma poi non può che arrivare alla meta. Ricordiamoci sempre che questo è ciò che vede chi si muove come l’aeroporto di partenza.

Passiamo all’aereo apparentemente impazzito… Tutto viene confermato: lui tende ad andare verso il centro, ma poi viene sbattuto verso l’esterno fino a uscire dalla piattaforma. Ovviamente, l’angolo tra aeroporto equatoriale e uscita dell’aereo deve essere sempre uguale ad α.

Concludendo: l’unica a raggiungere l’aeroporto finale è l’astronave che parte dall’equatore, proprio come ha indicato Andy. Non ho voluto ripetere ancora una volta tutta la costruzione della traiettoria. Inserisco, però, un altro “metodo” anch’esso abbastanza intuitivo. Utilizziamolo per il viaggio dell’aereo equatoriale, il più bizzarro dei quattro. Andiamo nella Fig. 6.

 

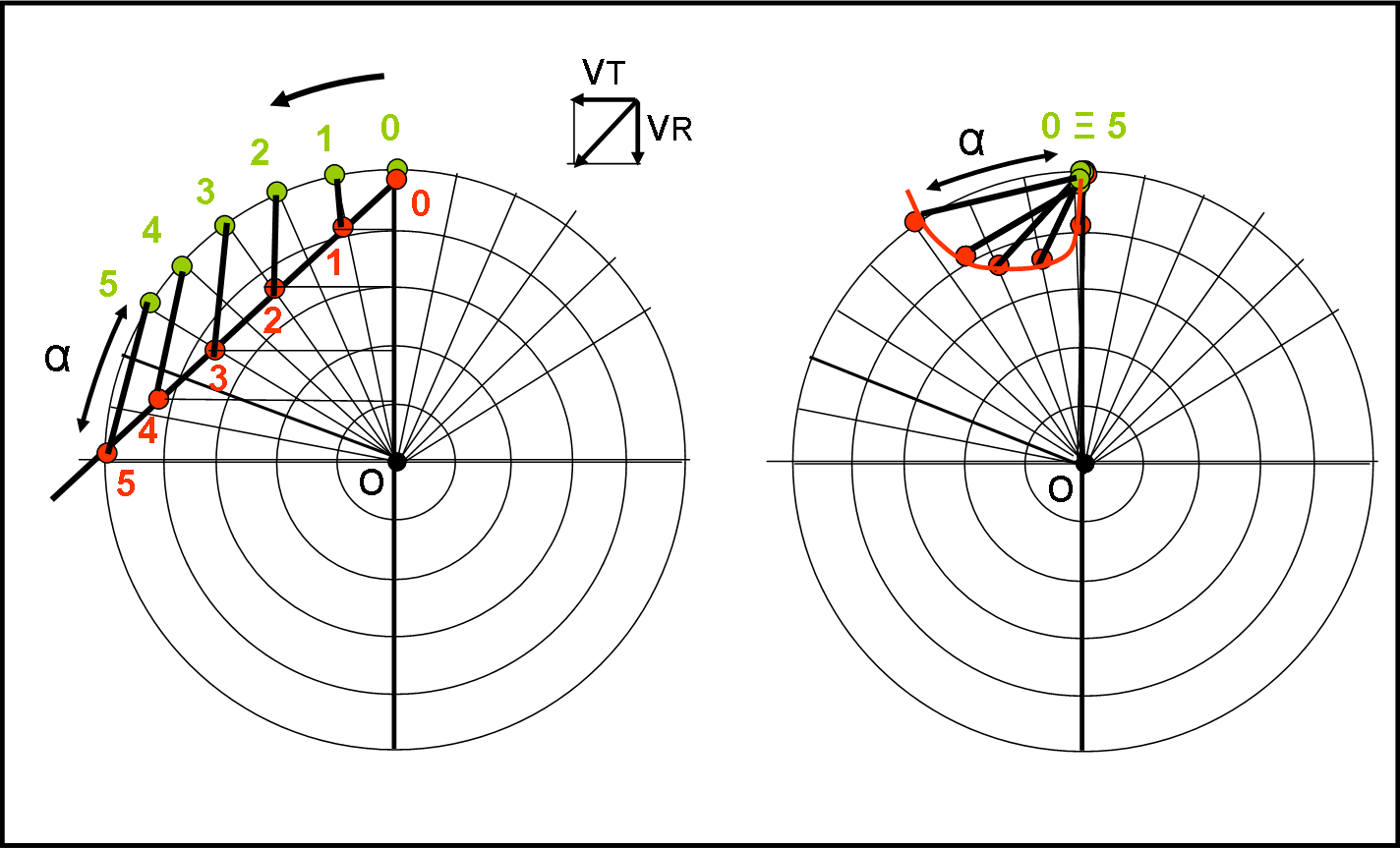
La divisione della figura di sinistra in tanti settori circolari uguali e in tanti cerchi concentrici ci dice solo che nel tempo che la pallina verde solidale con la piattaforma si porta sul raggio successivo, la pallina rossa si porterebbe su un cerchio più piccolo. Tuttavia, la pallina rossa subisce anche la velocità costante tangenziale e quindi si muove lungo la linea inclinata e le posizioni successive si trovano mandando le parallele orizzontali che partono dalle posizioni successive lungo la verticale (o combinando le due velocità coinvolte).

In poche parole, la pallina si muove nell’unità di tempo di un tratto che corrisponde a una velocità tangenziale (spazio percorso in senso orizzontale) sommata a una velocità radiale (spazio percorso in senso verticale), come mostrato nel piccolo diagramma di destra (somma vettoriale). Ne segue, ovviamente, che nello stesso tempo in cui la pallina verde percorre l’arco di cerchio, la pallina rossa si sposta di una certa quantità costante lungo la linea inclinata.

In conclusione, nei vari tempi considerati, pallina verde e pallina rossa devono trovarsi nelle rispettive posizioni: 1 con 1, 2 con 2, e via dicendo. Uniamo queste posizioni con un segmento rigido. Consideriamo adesso il “sistema” pallina verde, pallina rossa (e segmento che le unisce) e raggio relativo alla pallina verde ( O-1, O-2, ecc.).

Per vedere cosa succede nel sistema non inerziale (che si considera fermo), rappresentato nella parte destra della figura, bisogna riportare i vari raggi O-1, O-2, e tutto ciò che è “bloccato” a lui (come detto prima)… su quello di partenza (O-0), dato che tutti i pallini verdi devono coincidere, così come i raggi corrispondenti. La pallina rossa assumerà le posizioni successive viste nel sistema rotante. Ovviamente, l’angolo α deve essere lo stesso.

E tre! Un nuovo metodo per tracciare la traiettoria influenzata pesantemente dalla forza di Coriolis e da quella centrifuga. No, non fatevi prendere in giro... essi sono tutti la stessa cosa, anche se spiegati  in modo apparentemente diverso. Siamo di fronte, solo e soltanto, a un cambiamento di coordinate!

Ribadisco ancora che stiamo lavorando sempre con velocità rettilinee uniformi. Nulla ci vieterebbe di costruire le traiettorie anche con velocità sempre rettilinee, ma non costanti. Tuttavia, cambierebbe un po’ la forma della curva, ma il concetto di base no. Per cui possiamo anche permetterci di non complicare ulteriormente la faccenda. Questo varrà sia per i moti terrestri che per il moto del pendolo. Capire le forze agenti e la traiettoria finale nel sistema non inerziale è già un esercizio abbastanza intrigante e divertente.

Chi ha voglia (ma io preferisco non farlo per non creare troppa confusione) può fissare i valori di v_T e v_R e calcolare sia la velocità che le due accelerazioni fittizie, punto a punto. I moduli si ricavano semplicemente e per le direzioni e verso basta utilizzare bene la …mano destra (QUI)!

Io preferisco dedicarmi a un nuovo quiz (più correttamente una serie di costruzioni) che permetterà di capire meglio l’evolversi della situazione al variare della velocità e portarci qualitativamente verso il pendolo di Foucault. A presto!

 

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis