Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

 

A parte i piccoli problemi di salute che mi hanno un po’ bloccato, è giunta l’ora di risolvere velocemente i due ultimi quiz sui sistemi non inerziali e passare, poi, a tirare un po’ le somme, aggiungendo un minimo di … matematica. Forse, forse, avete capito che Coriolis & co. mi piacciono abbastanza...

A ben vedere, anche ciò che capita inserendosi in un sistema non inerziale assomiglia molto alle visioni “impossibili” di Erschel, così ben spiegate dal nostro amico Maurizio. L’unica vera differenza è che l’illusione prodotta in un osservatore rotante è un qualcosa di obbligatorio che deve essere introdotto per potere applicare sempre e comunque le leggi di Newton. Ricordiamoci che, se le velocità non sono relativistiche, la dinamica newtoniana basta e avanza anche per raggiungere al momento e al punto giusto un oggetto come Plutone o per fare di Cassini un osservatorio incredibilmente adatto per tutte le stagioni e per tutte le occasioni…

Tutti i nostri esempi e quiz sono serviti per avvicinarci a questo tipo di “illusione”, apparentemente assurda, attraverso approcci quasi infantili e riconducibili ad azioni di estrema semplicità. In realtà, sarebbe bastato il capitolo dedicato alla matematica dei sistemi relativi. Ma il nostro Circolo vuole sempre cercare di accontentare un po’ tutti…

Riflettiamoci un po’ sopra. Vi ricordate l’astronave che attraversa la Terra nello stesso tempo che un osservatore terrestre compie mezza rotazione attorno al proprio asse? Bene, è ovvio che si incontrano di nuovo dopo dodici ore ed è quindi ovvio che l’osservatore terrestre DEVE vedere l’astronave allontanarsi e poi tonare verso di lui. Non c’è niente di misterioso se lo guardiamo da un sistema inerziale: l’astronave percorre una traiettoria rettilinea e uniforme, mentre l’osservatore terrestre compie un arco di cerchio nello stesso identico tempo. Anche un bimbo capirebbe la situazione. Chiedendo, però, di vedere il tutto da chi ruota, ecco che, improvvisamente, spunta una curva molto strana e apparentemente illogica: come fa l’astronave a muoversi di moto circolare se sta andando dritta? La risposta è molto semplice: chi sta ruotando si sente fermo e riversa, su chi sta viaggiando tranquillamente, tutta la “stranezza” del suo moto (in questo caso una semplice rotazione).

Ne segue che i due quiz precedenti si risolvono facilmente utilizzando delle semplici strategie costruttive, sulle quali abbiamo “battuto” fin troppo. La soluzione è stata data subito sia da Arturo che da Daniela, ma penso che molti altri siano arrivati facilmente alla stessa conclusione.

Cominciamo dal primo (quello “costruttivo”…). Esso pone l’accento non solo sul moto rettilineo uniforme di un aereo che vola senza attrito su una piattaforma rotante, ma, partendo dal bordo esterno (aeroporto equatoriale) ed essendo vincolato ad esso, prima di lasciarsi andare a un tragitto libero e inerziale, DEVE conservare la velocità tangenziale che possedeva mentre stava ruotando parcheggiato in aeroporto. Questa situazione deriva direttamente dal principio d’inerzia: se eliminiamo la forza centripeta che obbliga ogni punto della piattaforma a ruotare, l’aereo (passato in un sistema inerziale) se ne va direttamente per la tangente, come ormai sappiamo molto bene.

La parte interessante di questa costruzione dipende, perciò, solo e soltanto da come si combina la velocità tangenziale “residua” con  quella del volo vero e proprio (v_T e v_R). Ovviamente la velocità risultante sarà sempre costante, ma inclinata rispetto a quella puramente verticale della direzione impostata dal pilota. La costruzione si ottiene con la solita somma vettoriale. In parole povere, partiamo da una traiettoria orizzontale (v_R = 0, l’aereo si stacca dall’aeroporto, ma non accende i motori), fino al caso in cui v_T = 0, ossia la velocità dell’aereo è talmente alta che la piattaforma può essere considerata immobile, ossia diventa un sistema inerziale.

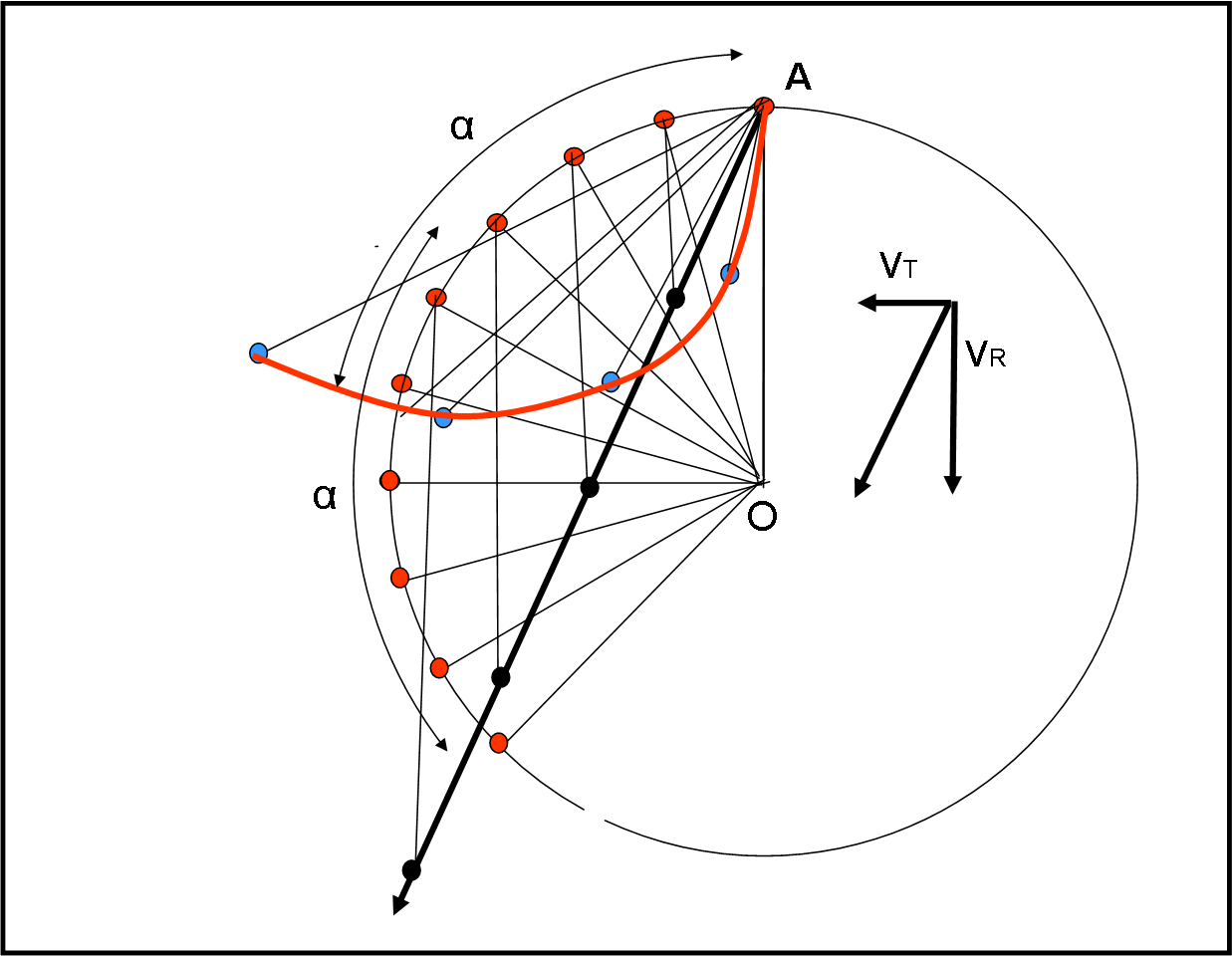
Se guardassimo le varie situazioni da un sistema inerziale, vedremmo la piattaforma (e l’aeroporto) ruotare, mentre l’aereo seguirebbe delle rotte rettilinee che partono da una orizzontale e finiscono a una verticale, come mostra la Fig. 1, dove ne abbiamo disegnata qualcuna a caso.

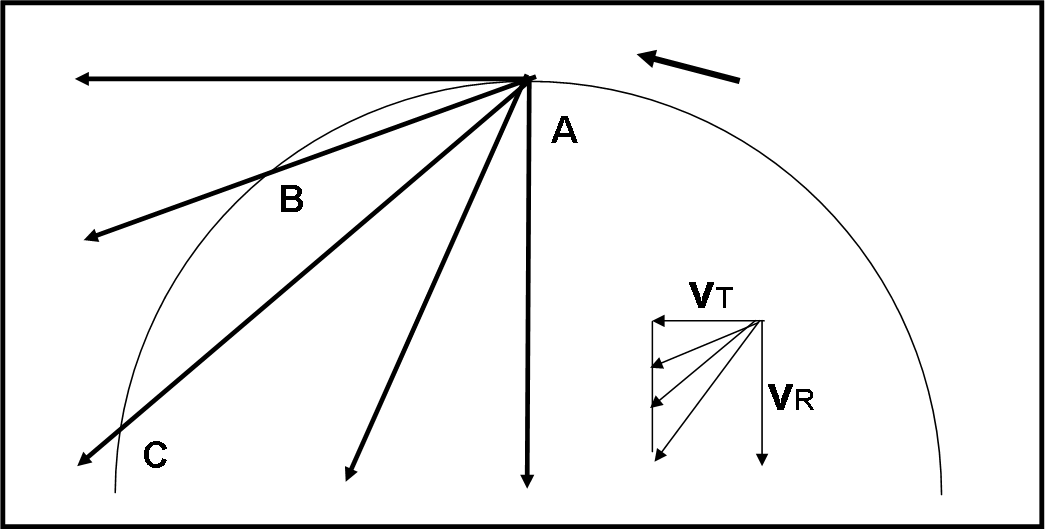
Per ottenere ciò, possiamo mantenere costante la rotazione (ossia v_T) e aumentare sempre più v_R. L’importante è notare che in due casi l’aereo abbandona la piattaforma in B e C. Ebbene questo è il fenomeno meccanico che dobbiamo mantenere, cambiando sistema di riferimento. L’arco AC o AB dovrà restare lo stesso anche se guardiamo lo strano volo dell’aereo restando fermi in aeroporto (l’arco -o angolo- non è altro che quello che abbiamo chiamato α in  questo articolo).

Mettiamoci al lavoro, utilizzando, ad esempio, il metodo grafico usato alla fine di questo articolo e otteniamo pochi esempi illustrati nelle Fig. 2, 3, 4 e 5. Nella Fig. 2 la velocità è tutta tangenziale e ritroviamo perfettamente quanto ricavato QUI. L’aereo, ovviamente, se ne va verso l’esterno, come una pallina a cui è stata tagliata la corda. L’angolo α è ZERO per entrambi i sistemi.

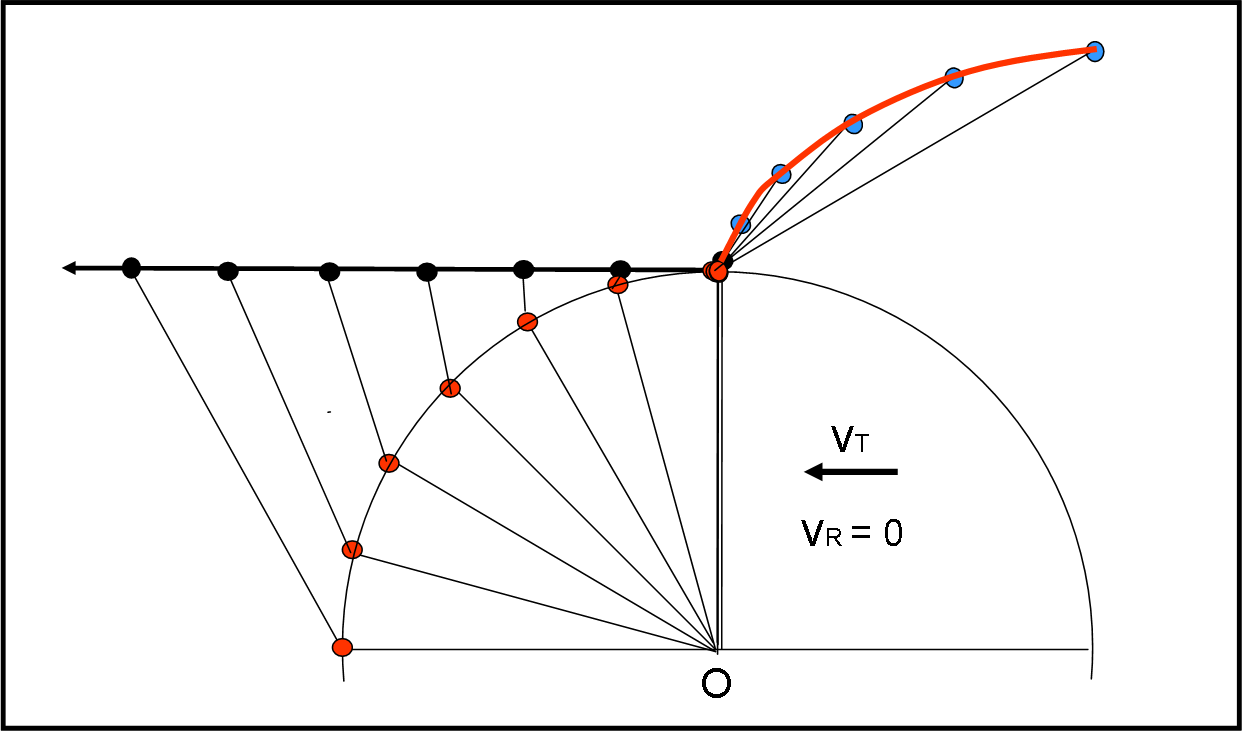
La Fig. 3 illustra un caso in cui l’aereo va veramente piano… Sembra quasi la traiettoria di prima, ma, se andiamo a “zoomare” sugli istanti iniziali, vediamo che l’aereo sembra fare un piccolo “giro” sopra l’aeroporto, per poi andarsene verso l’esterno. Quando l’aereo esce dalla piattaforma l’aeroporto si trova in A’ e quindi l’angolo α è praticamente zero o poco di più.

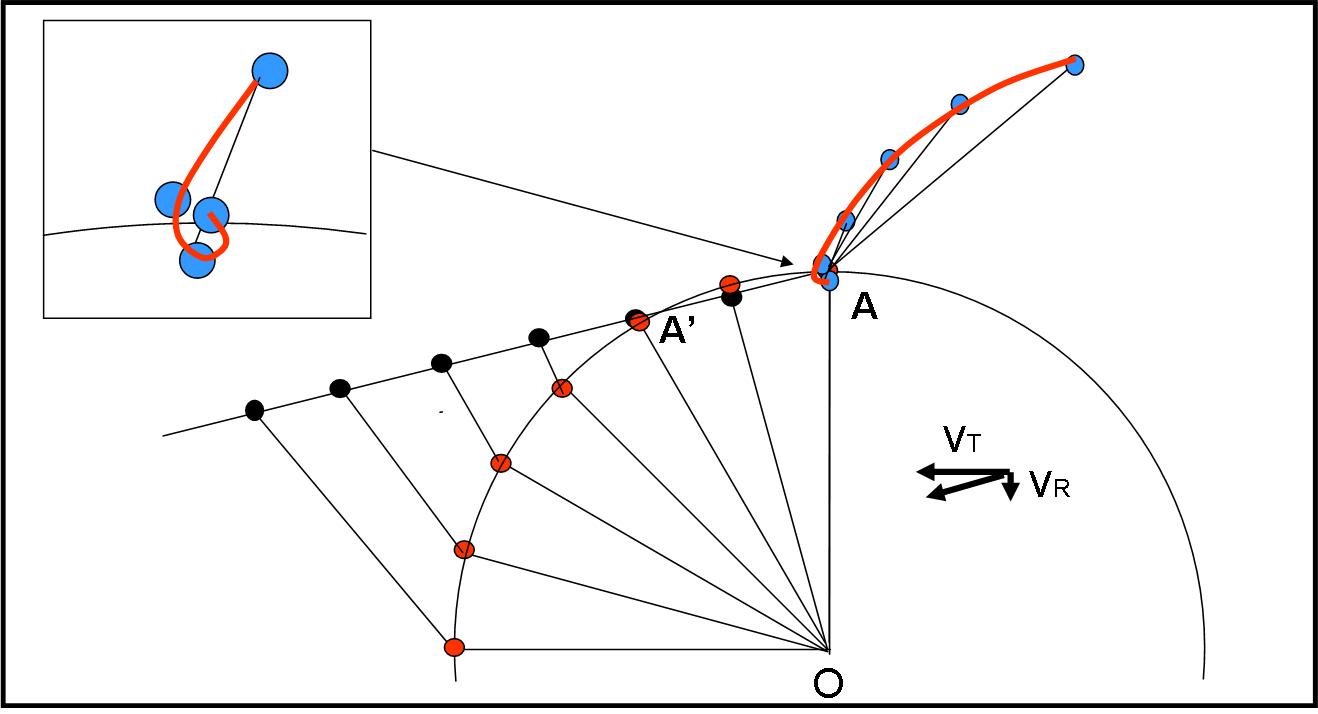
In Fig. 4 le cose si vedono molto meglio. Il giro sopra l’aeroporto si allarga e l’aereo esce dalla piattaforma quando l’aeroporto è arrivato in A’.

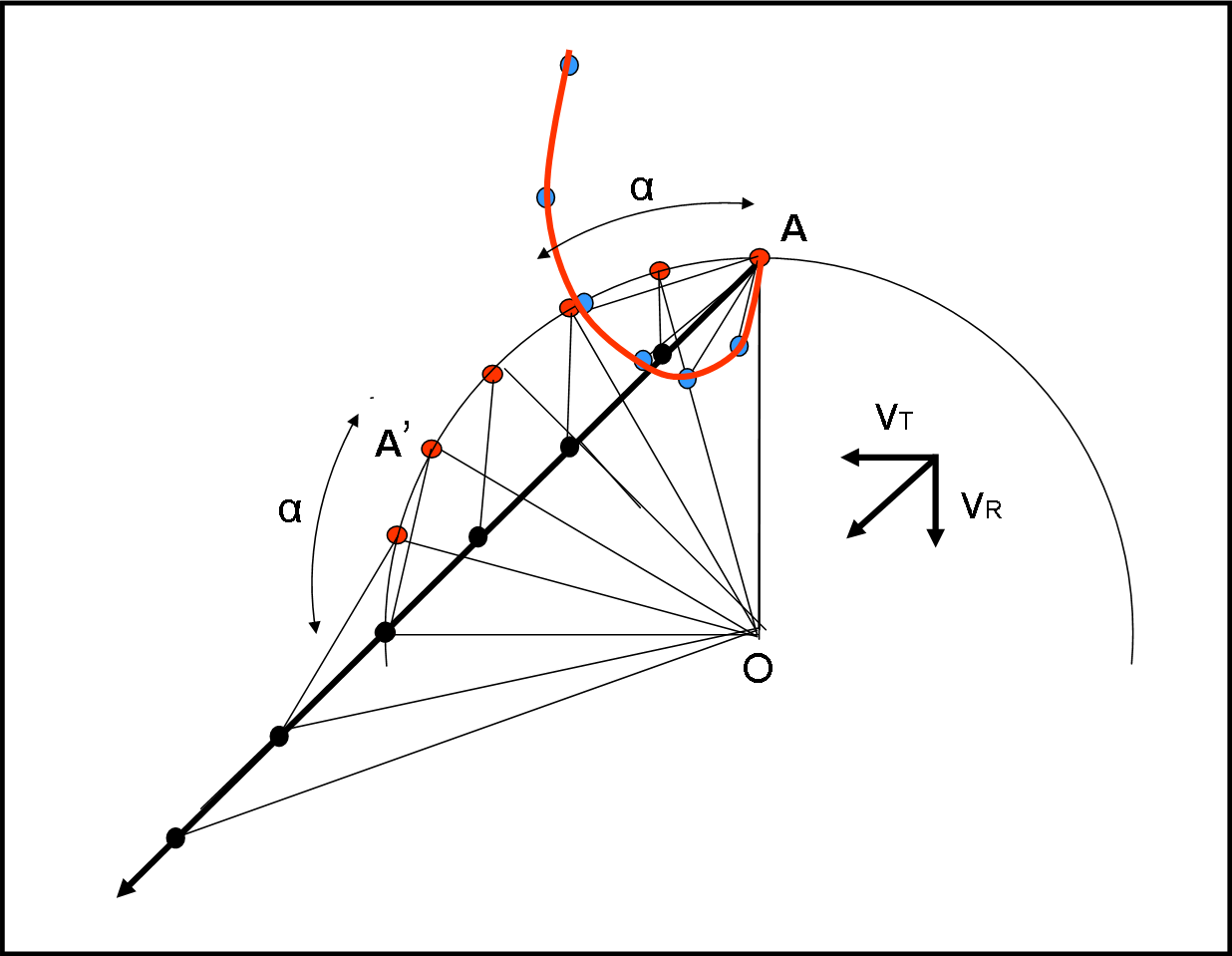
La Fig. 5 permette all’aereo di percorrere un discreto percorso prima di andarsene nello … spazio.

E via dicendo… come mostrato ancora meglio nei disegni aggiunti da Arturo nei commenti all’articolo del quiz, ma soprattutto nel regalo che ci ha fatto con le sue animazioni di facilissimo utilizzo. Un grazie di vero cuore!!!

https://ggbm.at/BYqFCPnH

Completamente diverso è il quiz “natalizio”, con tanto di autostrada. Anzi, è proprio il caso opposto: si vuole costringere il convoglio ad andare lungo una strada rettilinea costruita nel sistema rotante. Ovviamente, su Papalla, il convoglio viene visto seguire la strada “dritta” anche se con un po’ di fatica (lui sente comunque le forze fittizie che agiscono su di lui, come quando fate una curva in macchina). Dal sistema inerziale la faccenda acquista una ben diversa visione. Il convoglio non va assolutamente dritto, ma fa un lungo percorso spiraleggiante che lo porta al polo!

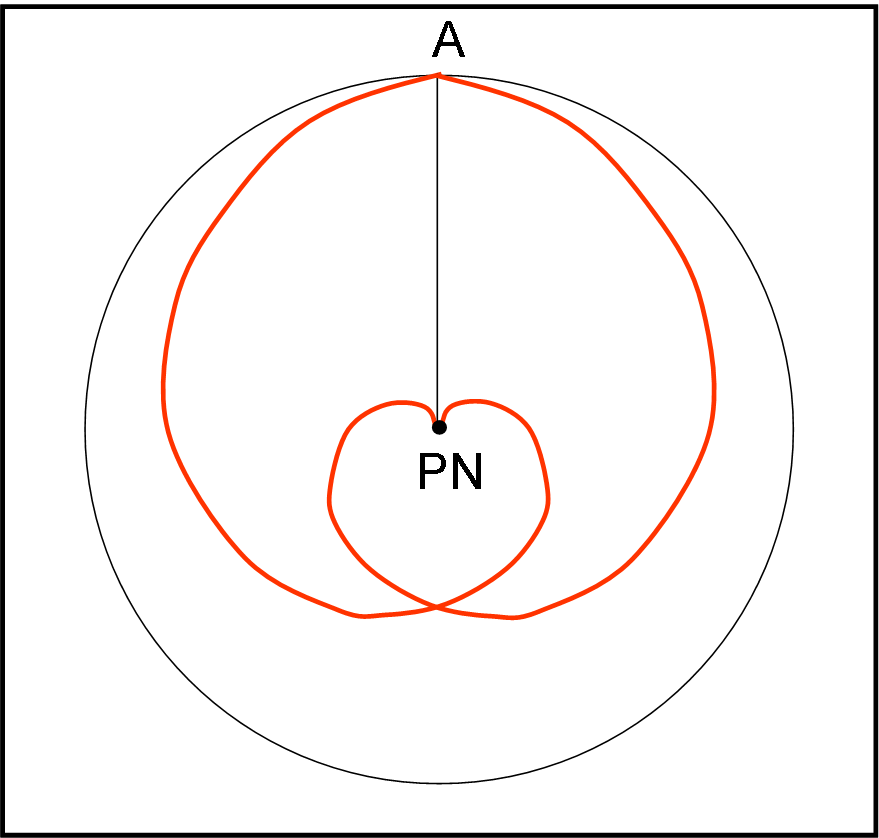
Oltre al moto percorso effettivamente nel sistema non inerziale si deve aggiungere il moto compiuto da tutto il sistema non inerziale. Qui non ci sono accelerazioni fittizie, ma solo accelerazioni vere; in particolare, quella centripeta che tiene il convoglio ancorato al suolo, come un lanciatore di martello che riduce sempre più la corda dell’attrezzo sportivo e viceversa. Per un’astronave, tra andata e ritorno si forma chiarissimo il simbolo del cuore ( anzi… due cuori!). Viva Natale!! Proprio come Daniela ha mostrato perfettamente nel suo commento.

Inseriamo la Fig. 6 che aggiunge, comunque, ben poco a quanto disegnato dalla nostra indispensabile e insuperabile “factotum” (e anche qualcosa in più…).

 

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis