Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

 

Il titolo sembra solo una constatazione e nulla più. Spesso viene presa come tale e da essa si innesca il discorso del Pendolo di Foucault e della rotazione della Terra. Tuttavia, esiste una dimostrazione molto pignola che fa uso dei prodotti scalari e vettoriali (di cui abbiamo parlato QUI). Farà un gran piacere agli amanti dei vettori e delle operazioni collegate.

Non ho intenzione di studiare a fondo il moto del pendolo, che può diventare anche piuttosto complicato. Tuttavia, per potere introdurre il pendolo di Foucault è quantomeno necessario averne una pur pallida idea.

In un sistema inerziale, sospendiamo una pallina P di massa m a un filo inestensibile fissato in O. Ipotizziamo che l’unica forza che agisca sulla pallina sia la forza di gravità F_G = mg (g può essere considerata costante). Se la posizione è verticale la tensione del filo (Fc) equilibra perfettamente quella di gravità e la pallina è in equilibrio stabile (Fig. 1a). r è il vettore distanza tra O e la pallina P.

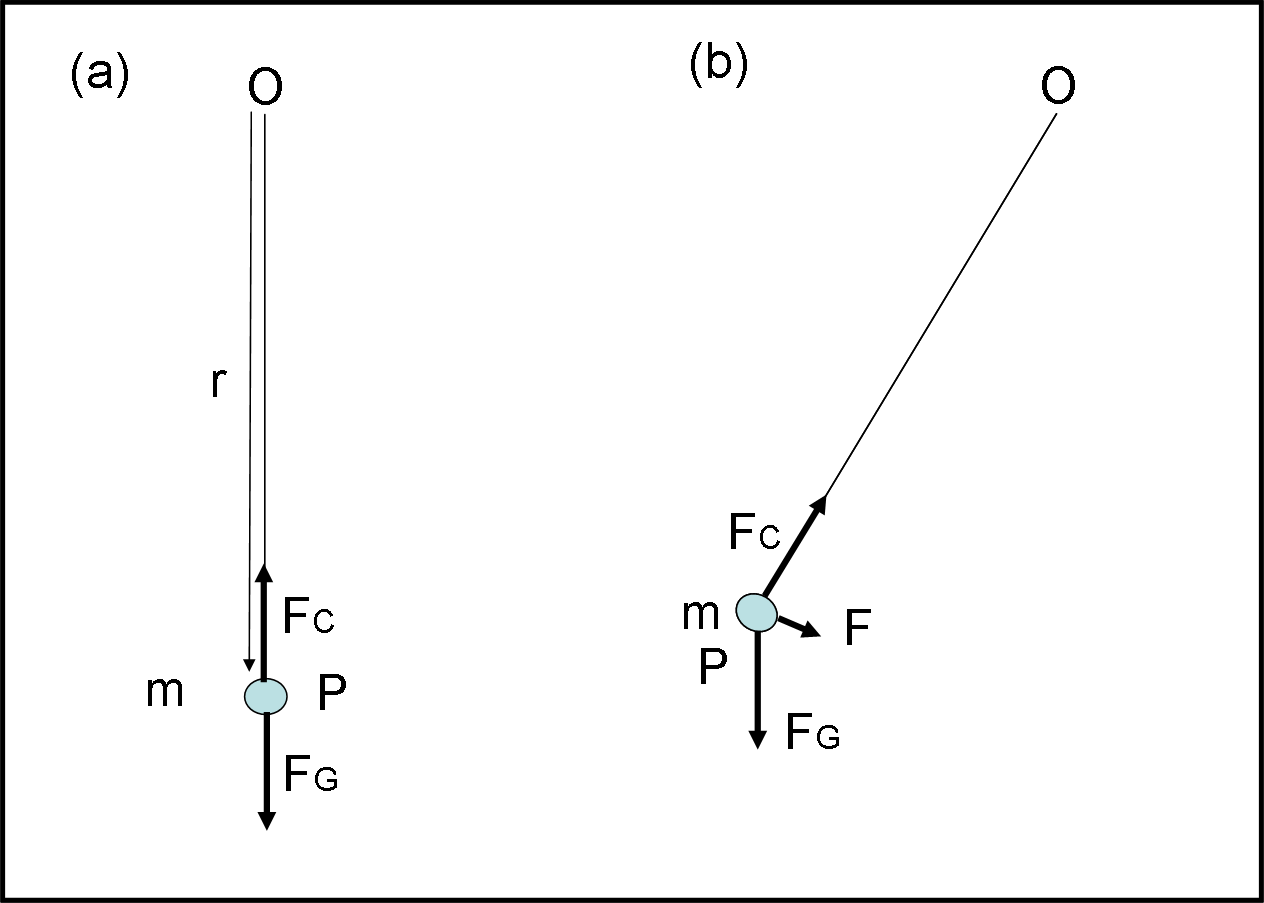
Spostiamo, adesso, la pallina P rispetto alla verticale, comunque si voglia, e lasciamola libera. Otterremo il ben noto moto del pendolo, dove la pallina raggiunge un altezza massima, con velocità uguale a zero, poi ricade verso il basso sorpassando la posizione di equilibrio verticale e risale nella direzione opposta fino a un’altezza uguale a quella di prima, e via dicendo, in assenza di attriti vari (Fig. 1b).

Il moto del pendolo viene spesso usato per descrivere la conservazione dell’energia, dato che nel punto più alto l’energia cinetica è zero (v = 0), mentre è massima quella potenziale. Nel punto più basso (posizione verticale) l’energia potenziale è minima, ma è massima quella cinetica e via dicendo, un po’ come nelle montagne russe.

Le uniche forze in gioco sono quella di gravità e la tensione del filo che non è altro che una forza centripeta. Normalmente, si dice che per questa ragione il moto deve avvenire esattamente nel piano individuato dalle due forze. La conclusione sembrerebbe ovvia, ma sapete che spesso i matematici sono un po’ paranoici e vorrebbero la garanzia che spostando la pallina in qualsiasi posizione rispetto a quella di equilibrio verticale si ottenesse sempre e comunque un piano di oscillazione invariante.

Prendiamolo, perciò, come un giochino vettoriale, molto utile per sveltire la mano destra e per ricordare anche il prodotto scalare. Le formule sono semplicissime e basta solo un minimo di ragionamento.

Dalla seconda legge di Newton sappiamo che:

F = ma

Nel pendolo semplice, come già detto, sulla pallina P, di massa m, agiscono solo due forze: quella di gravità  (mg) e la reazione del filo (forza centripeta) Fc.

Possiamo allora scrivere  che l’unica forza agente è la somma vettoriale delle due forze reali (siamo in un sistema inerziale).

F = ma = Fc + mg

m dv/dt = Fc + mg             …. (1)

Consideriamo adesso il vettore definito dal prodotto vettoriale r ∧ g (perpendicolare al piano contenente r e g) e moltiplichiamo scalarmente entrambi i membri della (1) per lui:

m dv/dt  × (r ∧ g) =  Fc  ×  (r ∧ g)  - mg  × (r ∧ g)

Ricordiamoci che il prodotto scalare è uno scalare che si annulla quando i vettori sono perpendicolari tra loro (nel modulo compare il coseno). Il prodotto vettoriale, invece, è un  vettore che si annulla quando i vettori sono paralleli tra loro (nel modulo compare il seno).

Per costruzione sia Fc che g sono perpendicolari a (r ∧ g) e quindi i prodotti scalari del secondo membro devono valere ZERO. Ne segue:

m dv/dt  × (r ∧ g)  = 0

La massa non è zero e quindi abbiamo:

dv/dt × (r ∧ g)  = 0           …. (2)

Consideriamo, adesso, l’espressione:

d(v × r ∧ g)/dt =  dv/dt  ×  (r ∧ g) + v  ×  (dr/dt ∧  g) + v  ×  (r ∧ dg/dt)

Tuttavia, v non è altro che dr/dt, per cui il vettore (dr/dt ∧ g) deve essere perpendicolare a v; da che ne consegue che il prodotto scalare deve annullarsi. Inoltre, g può essere considerata costante per cui anche l’ultimo termine va a zero. Otteniamo, perciò, ricordando la (2), che:

d(v × r ∧ g)/dt  =  dv/dt  × (r ∧ g) = 0

Ne segue che v × r ∧ g = costante

Tuttavia, nei punti di inversione del moto del pendolo la velocità deve essere zero per cui deve essere uguale a zero anche la costante.

v × r ∧ g = 0

da cui segue che i tre vettori devono essere complanari!

Infatti, r ∧ g non è uguale a zero e, quindi, per ottenere zero, v deve essere perpendicolare a questo vettore, ossia stare nel piano dei primi due.

Bene, adesso siamo sicuri che il piano del pendolo è un invariante e che, quindi, quando lo trasferiamo in un sistema non inerziale, è tutto il piano che subisce le forze apparenti

 

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis