Categorie: Fisica classica
Tags: forza centrifuga forza di Coriolis orso polare pendolo piattaforma quiz rotazione Terra
Scritto da: Vincenzo Zappalà
Commenti:5
QUIZ: le osservazioni di un orso polare (in perfetta salute) **
Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.
Vorrei sfidare chiunque, che sia giunto esattamente al Polo Nord, a dimostrare che la Terra non sia piatta. Soprattutto se può muoversi di solo pochi metri attorno all’asse polare (ultimamente lo hanno dipinto di rosso per ricordare che il clima terrestre è ormai veramente “bollente”). Toccando l’asse polare (non muovetelo troppo, mi raccomando…) si avverte, però che, anche se piatta, la Terra gira attorno a quell’asta che punta quasi perfettamente verso la stella polare (le farà mica il solletico?).
Se siete raccomandati o se avete molti quattrini potreste anche eliminare per un po’ di tempo l’asse polare vero e proprio, dato che la Terra ha una sua autonomia e continuerebbe a girare anche senza di lui. Al suo posto, potreste sistemare un ben pendolo che vi siete portati da casa e montarlo, seguendo istruzioni molto accurate che evito di enunciarvi. L’importante è che il filo del pendolo sia posizionato esattamente lungo l’asse terrestre. La sfera terminale è in grado di far scendere lentamente della polvere finissima di carbone. Poi, non vi resta che ricordare la piattaforma rotante e quella forza malandrina di Coriolis insieme alla sua degna compare centrifuga.
Finiamo di fare gli … idioti e parliamo più seriamente, facendoci aiutare dalla Fig. 1, dove la piattaforma piatta IMMOBILE (vincolata perfettamente alla superficie terrestre in quella piccola zona) è vista dal punto di sospensione del pendolo S. La sfera con la polvere sia P, in condizioni di equilibrio, ossia esattamente lungo la verticale del filo. Tutto è immobile o, almeno, sembra… (a parte un orso bianco in piena forma, inseguito da ambientalisti che vogliono misurargli la febbre a tutti i costi…).
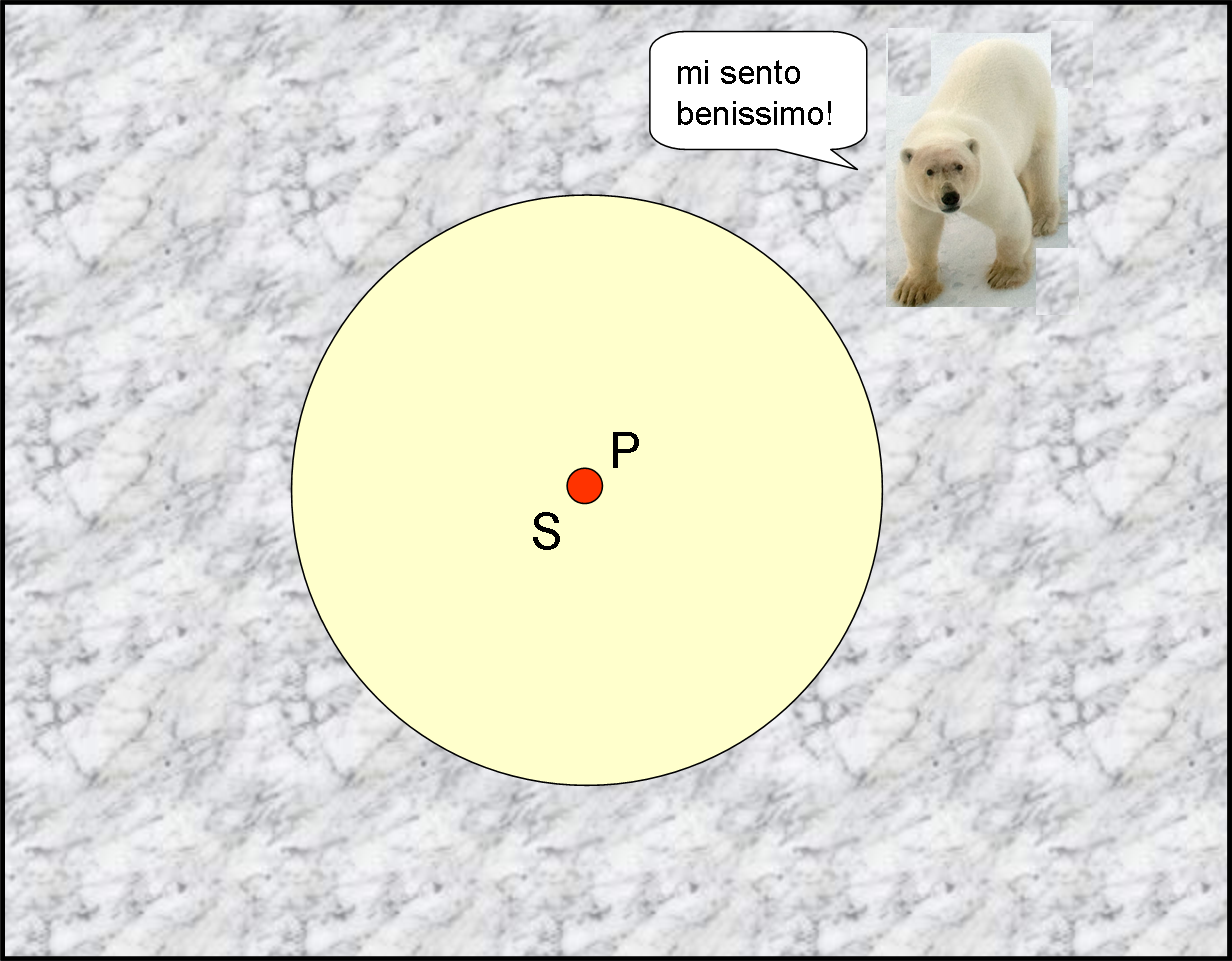
La faccenda, se non si considera il filo del pendolo, sembra esattamente quella che ci è servita varie volte per evidenziare le forze fittizie nella piattaforma rotante. Questa volta, però, non abbiamo bisogno di far ruotare la piattaforma, dato che essa gira insieme alla Terra attorno all’asse di rotazione individuato da P e/o S. Il suo moto è, ovviamente in senso antiorario, e compie un giro completo in 24 ore. Non è una grande velocità angolare, ma sufficiente a causare effetti ben visibili sul moto della sfera S, una volta che il pendolo sia stato messo in moto.
Basta, ora, lasciare libertà all’orso bianco e permettergli di dare il via al pendolo per fargli compiere il proprio mestiere, lasciando una traccia scura sulla piattaforma, mentre si muove da un estremo all’altro di essa, seguendo le regole che abbiamo brevemente descritto QUI.
L’orso è molto interessato (è riuscito a disperdere gli ecologisti assatanati) e, dopo 24 ore, è veramente soddisfatto dalla figura che ha visto descrivere dal pendolo e vuole provare di nuovo, ma, questa volta, osserva un disegno leggermente diverso.
(1) Come mai? (2) E quali sono i due disegni che ha visto descrivere? (3) Ovviamente, ci sta bene anche una spiegazione molto empirica e non matematica…
Ah… un certo Foucault si trovava di passaggio da quelle parti e ha rubato l’idea all’orso bianco… senza dargli alcun compenso…. E poi diceva di essere un amante degli animali …
Fate in fretta... perché sta per arrivare un ... ciclone!!!!
QUI la soluzione
In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis






5 commenti
Forza! Non abbiate paura degli orsi bianchi (questo ha già mangiato ed è pacifico). In fondo basta applicare quanto già sappiamo molto bene... una vera banalità...
Caro Vincenzo, non sono sicuro di avere capito la situazione. Mi sfugge qualcosa. Ad un certo punto , nel testo, scrivi che la sfera con la polvere sia P, in condizioni di equilibrio, ossia esattamente lungo la verticale del filo. Ciò mi fa pensare ad un pendolo fermo, con il peso (in questo caso la sfera) immobile. Poi, più avanti, scrivi che la velocità con cui ruota la piattaforma insieme alla Terra non è una grande velocità angolare, ma sufficiente a causare effetti ben visibili sul moto della sfera S. E infine scrivi di "permettere al pendolo di fare il suo mestiere, lasciando una traccia scura sulla piattaforma, mentre si muove da un estremo all’altro di essa".
Si deve dunque considerare il pendolo che si muove , e cercare di capire cosa disegnerà sulla piattaforma la polvere che cade dalla sfera in oscillazione ?
Chiedo scusa per l'eventuale banalità della domanda, ma se qualcosa non mi quadra vado in loop e mi blocco
Chiedo scusa io, caro Arturo, per essere stato poco chiaro... Ho aggiunto qualche parola e... sì, è proprio quello che intendi tu. La piattaforma ruota perché ruota la Terra e l'orso ha messo in moto il pendolo, ottenendo però due tipi di disegno diversi a seconda delle condizioni secondo cui ha messo in moto il pendolo...
Scusate ancora per l'ambiguità della spiegazione... ma con questi orsi bianchi non si sa mai come comportarsi....
ma con questi orsi bianchi non si sa mai come comportarsi.... 
Probabilmente, se non ho male interpretato, i disegni differenti tracciati sul piano di oscillazione dipendono dal punto di inizio dell'oscillazione, ossia partendo dal bordo della piattaforma di rotazione oppure dal suo centro.
In ogni caso siamo in presenza di un moto (da parte del pendolo) non a velocità costante, ma che si ripete per intervalli di tempo regolari (trascurando la dissipazione dell'energia dovuta all'opposizione dell'aria).
È una continua trasformazione di energia potenziale (massima alle 2 estremità dell'oscillazione, velocità relativa pari a zero) in energia cinetica (massima quando il pendolo si trova sulla sua verticale rispetto al piano di oscillazione, velocità relativa massima).
Qui c'è un video che visualizza bene il fenomeno:
https://www.youtube.com/watch?v=VPxu1zANe0c
P.S.
Enzo ha scelto proprio il polo Nord (sarebbe stato lo stesso anche al polo Sud), dove la rotazione completa del piano di oscillazione si compie in 24 ore; a qualunque altra latitudine la rotazione si compie in un tempo superiore; (all'equatore.....ve lo dirà Enzo )
)
Il tempo di rotazione del piano di oscillazione dovrebbe seguire questa legge:
t = (24h/sen α) x (θ°/360°)
dove
- t è il tempo (espresso in ore) necessario al piano di oscillazione per ruotare di θ°;
- θ° è la rotazione del piano di oscillazione, intorno all’asse passante dal punto di aggancio del pendolo e il centro del piano di rotazione, ortogonale al piano stesso, espressa in gradi;
- α è la latitudine del luogo dove “pendola il pendolo”, espressa in gradi;
- 24h (24 ore) 1 periodo di rotazione della Terra attorno al proprio asse (considerando il giorno solare e non quello siderale).
Perdonami Enzo se non ho correttamente interpretato e/o anticipato qualcosa per quando scriverai sul pendolo di Foucault
caro Andy,
sono ben contento dell'interpretazione... oltretutto posso dire che tu hai scelto esattamente il video che avrei inserito io nella risposta (o siamo entanglati o sei amico dell'orso....). Si potrebbe aggiungere ancora qualcosina: ... qual è il moto del pendolo nel sistema inerziale, nei due casi?
Comunque... sempre bravo. Mi sento sempre di più le spalle sicure, grazie amici maghi, maghetti e assistenti maghi... Per stare in questo Circolo bisogna essere tutti un po' maghi o almeno un po' speciali!
Volevo aggiungere una nota per tutti o quasi:
Se avete argomenti che volete che tratti in modo particolare (a livello divulgativo) scrivetemelo e vedrò di parlarne. Collaborazione a 360°!!!!!!