Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO.

 

Praticamente Andy ha risolto il QUIZ dell'orso bianco e io chiedevo solo una piccola informazione in più, che è scivolata nei commenti. Comunque sia, il nostro orso bianco non ha fatto altro che “inventare” il pendolo di Foucault nella sua posizione più favorevole: il polo terrestre.

Non è molto che abbiamo dimostrato come il piano del pendolo sia immutabile. Ne segue che, messo in moto nelle condizioni più favorevoli, esso non può che proiettare una linea retta sulla superficie della piattaforma, andando avanti e indietro. Tuttavia, la piattaforma ruota insieme alla Terra attorno al polo, da cui segue che la traccia di polvere lasciata dal pendolo non può mai essere la stessa.

In fondo, è quello che abbiamo già trovato lasciando libera una pallina di attraversare, con una certa velocità rettilinea una piattaforma girevole. Nel sistema di riferimento rotante il percorso della pallina è tutt’altro che rettilineo. La stessa cosa deve capitare anche alla traccia lasciata dal nostro pendolo polare. Proprio il fatto che la linea sia curva ci impone la presenza della forza centrifuga e di quella di Coriolis.

Benché fin dall’antica Grecia (e forse anche prima) si ipotizzava, di tanto in tanto, una rotazione della Terra, nessuno era mai riuscito a dimostrarlo in modo così eclatante come con il pendolo di Foucault. L’unico modo per spiegare come mai un pendolo non mantenga fisso il proprio piano di oscillazione non può che essere la rotazione di quello che gli sta sotto, ossia l’intero pianeta.

Siamo in periodo natalizio e le decorazioni per le strade e sugli alberi si moltiplicano. Ebbene, anche il nostro pendolo disegna delle bellissime figure di tipo stellare che sembrano proprio adatte allo scopo. Essenzialmente loro sono di due tipi e ciò dipende da come è stato messo in moto il pendolo.

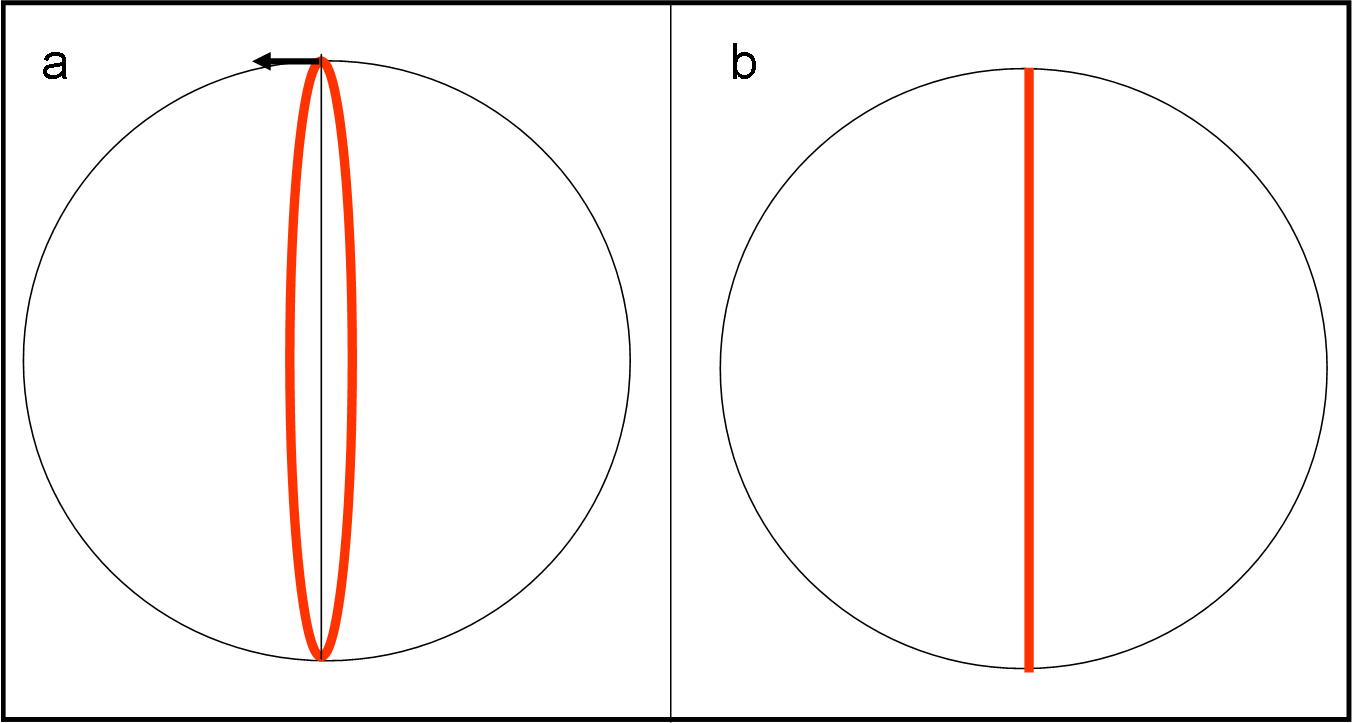
Se esso viene mosso (senza imporgli strani spostamenti iniziali) quando è in condizioni di equilibrio (filo verticale e sfera immobile), il moto del pendolo è veramente rettilineo nel sistema inerziale (Fig. 1b) e siamo nel caso trattato QUI.

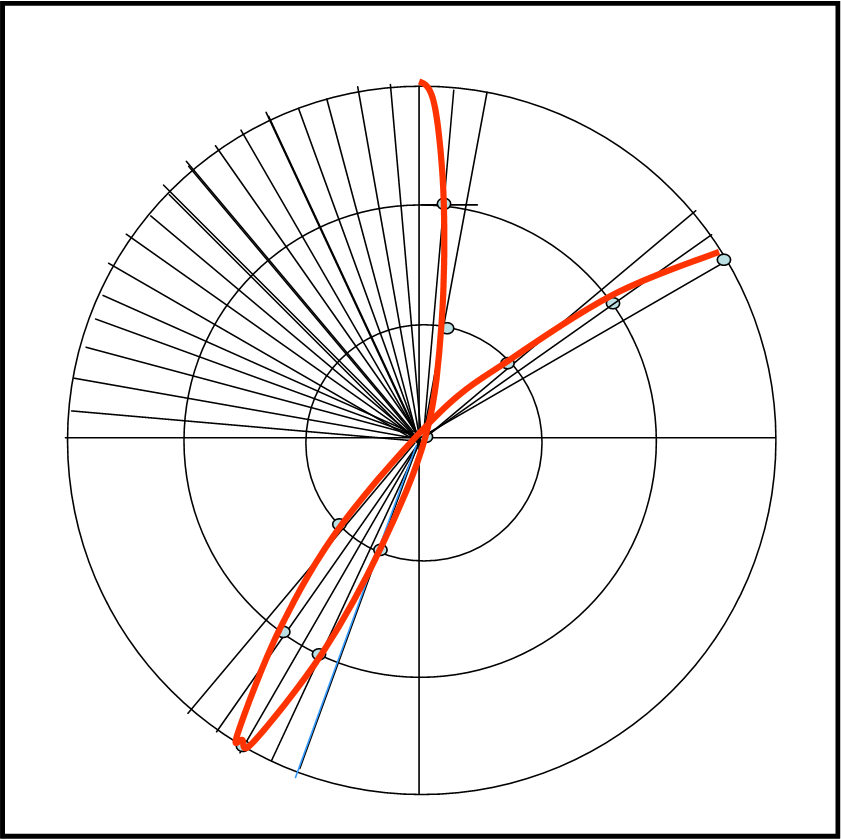
La figura che ne segue (Fig. 2b) è una specie di fiore con tanti petali (la quantità dipende dalla velocità del pendolo rispetto alla velocità di rotazione).

Essendo partito dal punto centrale, ogni traccia lasciata dalla sfera deve passare per tale punto. La costruzione geometrica del “fiore” viene mostrata in Fig. 3.

Il pendolo, però, può anche iniziare il suo percorso ponendo la sfera a una certa altezza dalla piattaforma. Anche se l’orso la lascia libera senza dare scossoni laterali, è indubbio il fatto che la sfera si trovi a una certa distanza dall’asse polare e quindi debba conservare la velocità tangenziale che ha anche l’orso (principio d’inerzia). Siamo nel caso trattato QUI.

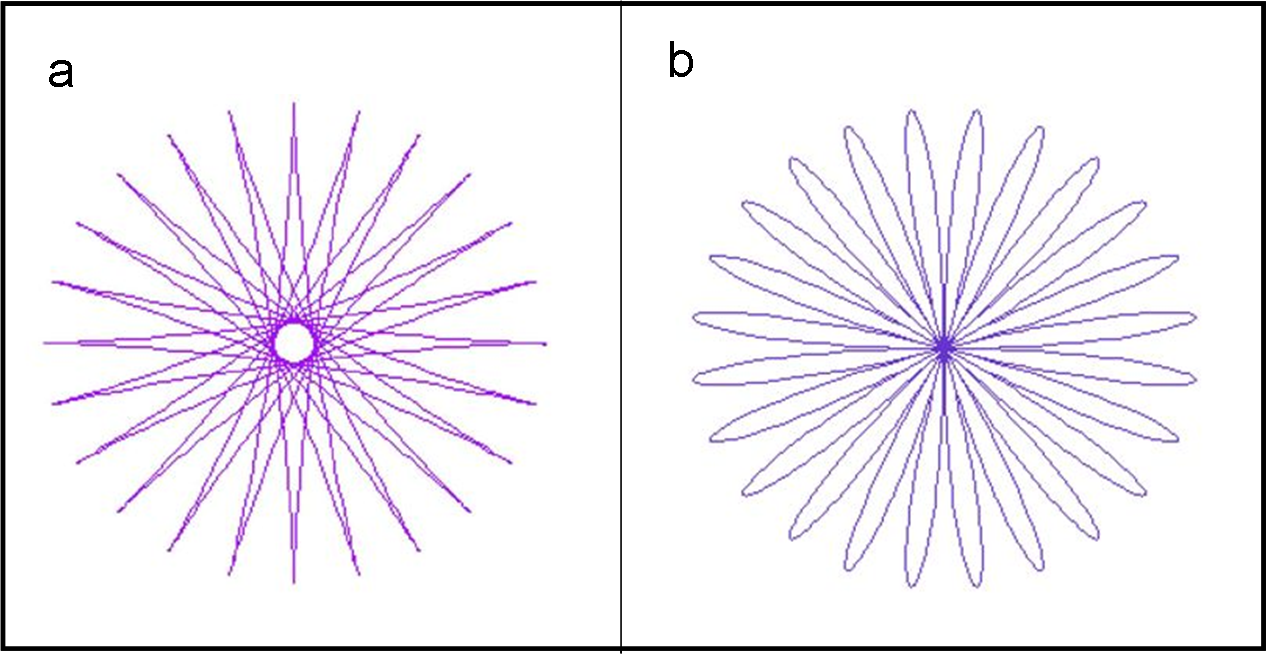
Tuttavia, la sfera non è libera di proseguire lungo la linea che si ottiene sommando la velocità di attraversamento della piattaforma e di quella tangenziale, dato che è pur sempre vincolata al punto di sospensione: il filo non è estendibile e mantiene sempre la stessa lunghezza. Siamo di fronte a una specie di pendolo conico, e  -senza entrare in dettagli inutili- la traiettoria descritta dalla sfera  lascia come traccia un’ellisse (nel sistema di riferimento inerziale) (Fig. 1a), che si trasforma in tante linee curve che danno luogo a una specie di stella, con tante punte, nel sistema rotante (Fig. 2a). Si può notare  che la traccia non passa mai per il centro, ossia per il punto di equilibrio stabile.

Il video che segue (già proposto dal nostro amico Andy) mostra  i due casi in modo perfetto.

A questo punto, prima di spostarci dal polo e lasciare il nostro orso a divertirsi con chissà quanti altri movimenti più che bizzarri, è forse giusto ribadire un concetto che a volte può creare un po’ di confusione: “In pratica, cosa vede un alieno al di fuori del sistema rotante della Terra? Vede una traccia sempre uguale o vede proprio crearsi un po’ alla volta le figure descritte precedentemente?”. Ovviamente la risposta giusta è la seconda!

Ricordiamoci sempre che il fenomeno fisico deve rimanere lo stesso: cambia solo il modo di spiegarlo!

A mano a mano che la polvere cade dalla sfera, la piattaforma si muove sotto di lei e quindi l’alieno non può che vedere una traccia curva. Tuttavia, per lui la motivazione è proprio quella VERA, ossia un qualcosa di rettilineo (o lievemente ellittico), nel suo sistema, lascia una traccia curva dato che il “foglio da disegno” continua a cambiare posizione. Non solo, ma anche i due tipi di figura hanno un senso reale. In un caso il pendolo parte da fermo e non ha velocità trasversale al moto, mentre nell’altro il pendolo parte con una leggera velocità trasversale che deriva alla rotazione di chi lo ha in mano prima di lasciarlo.

L’orso bianco, invece, si considera fermo e per spiegare quelle strane curve lasciate dalla sfera è obbligato a introdurre delle forze fittizie che agiscano su di lei.

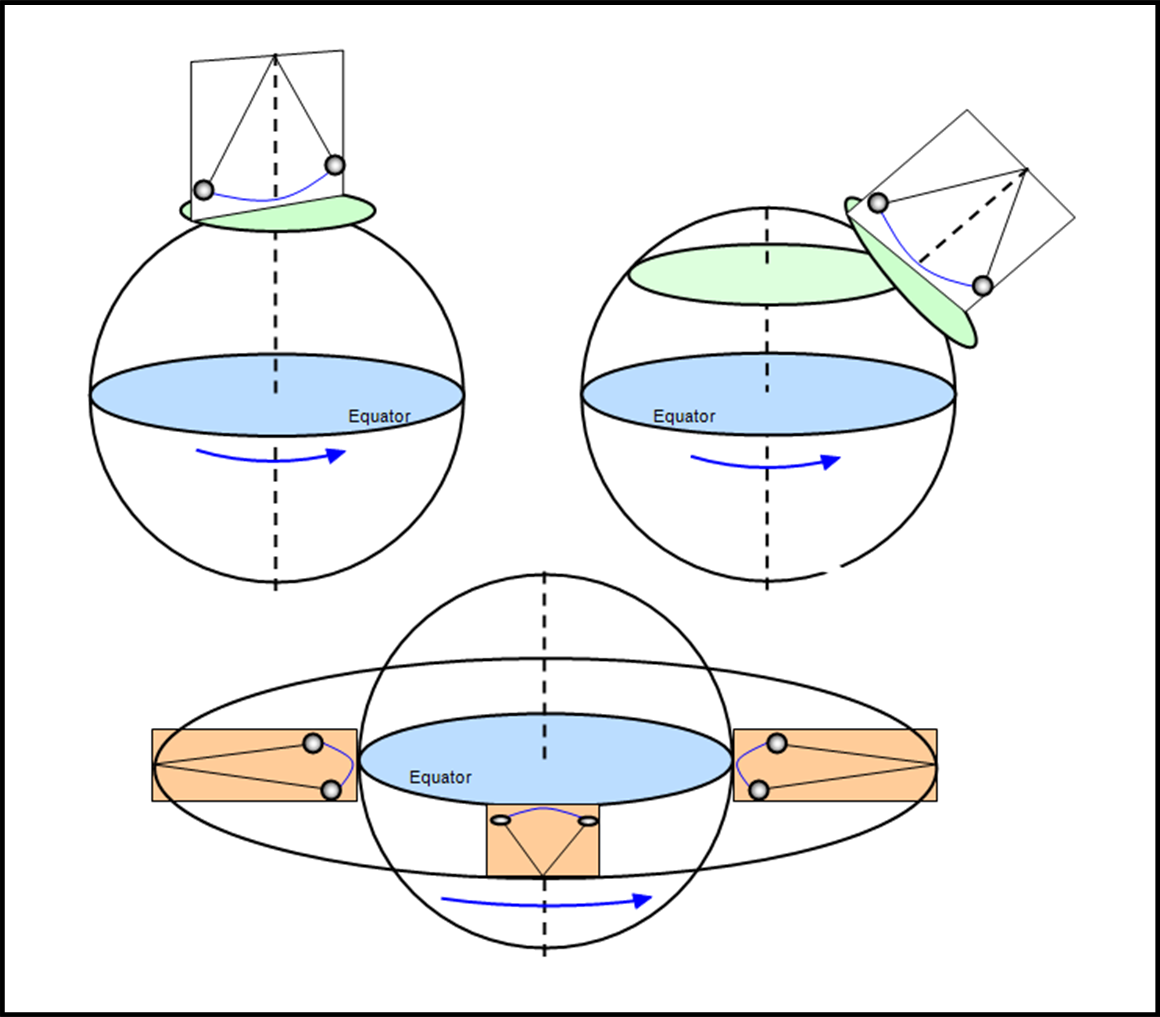
Per completare la trattazione dovremmo descrivere cosa succederebbe se il pendolo non fosse più appeso al polo nord (o sud), ma in un luogo qualsiasi della Terra (a latitudine φ). E’ cosa ovvia che il pendolo continui a oscillare tranquillamente in un unico piano se lo portassimo all’equatore, dove il vettore velocità angolare della Terra è perpendicolare al filo del pendolo (Fig. 4).

Più complicata è la faccenda per una latitudine qualsiasi. La cosa migliore sarebbe esprimere compiutamente l’equazione del moto del pendolo, ma vi assicuro che non è cosa semplice (un po’ come risolvere l’equazione del moto dei due corpi). Direi proprio di evitarla e limitarci a ciò a cui ha già accennato Andy nel suo commento.

Basta poco per rendersi conto che più la latitudine φ diminuisce e più è lungo il tempo necessario al pendolo per completare la sua figura.

Se il punto di sospensione non appartiene all’asse terrestre, ma si trova alla latitudine φ, la velocità angolare ω ha una componente radiale ω sin φ e una componente tangente al meridiano, Fig. 5.

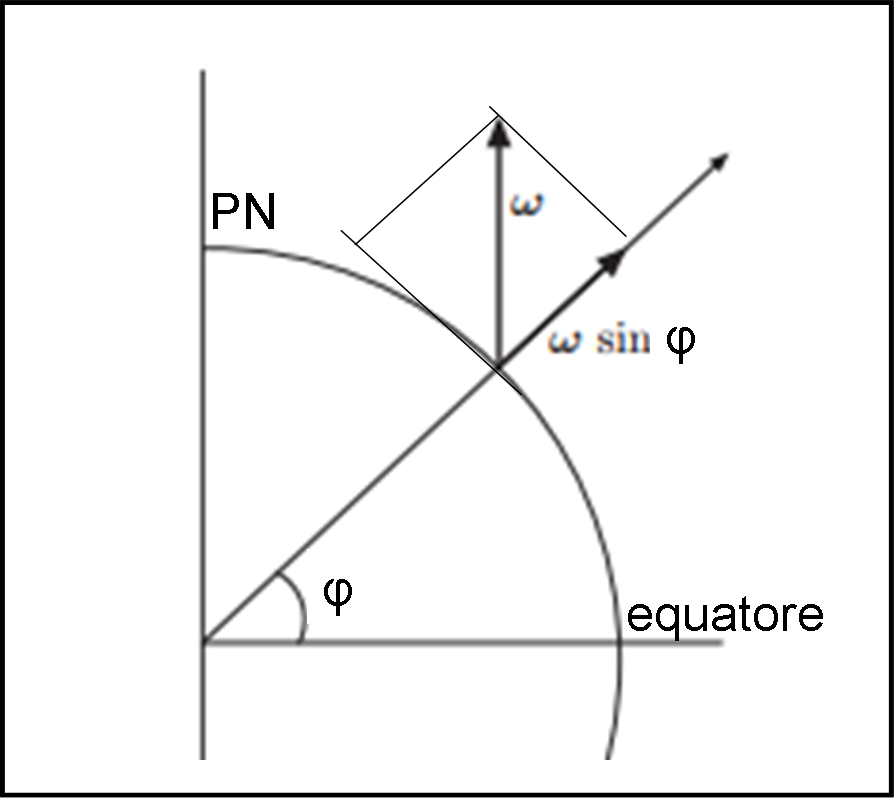
Quest’ultima, per piccole oscillazioni è inefficace. Dunque, alla latitudine φ, il piano di oscillazione del pendolo ruota attorno ad un asse verticale con velocità angolare ω_φ = ω sin φ.

Possiamo, allora, scrivere, chiamando P_φ il periodo di rotazione completa del pendolo:

ω_φ = 2π/P_φ = ω sin φ = (2π/P) sin φ

1/ P_φ = sin φ/P

P_φ = P/sin φ = 24^h/sin φ

Per φ = 90°, otteniamo P_φ = P (polo)

Per φ = 0°, otteniamo P_φ = 1/0 = infinito

 

In attesa che siano terminati ed inseriti in unico approfondimento, QUI trovate tutti gli articoli finora scritti sulla forza di Coriolis