Categorie: Fisica classica
Tags: accelerazioni fittizie anticicloni caduta dei gravi cicloni forza centrifuga forza di Coriolis forze fittizie Guglielmini leggi di Newton moti relativi moti rotatori pendolo di Foucault piattaforma rotante principio di inerzia sistemi di riferimento sistemi inerziali sistemi NON inerziali
Scritto da: Vincenzo Zappalà
Commenti:25
Gira, il mondo gira: sistemi inerziali e non, moti relativi, forza di Coriolis... **/***
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.
Questo lungo articolo raccoglie una lunga serie di articoli singoli e vuole arrivare a spiegare la forza di Coriolis, una forza "fittizia" come la "centrifuga". Esse, a volte, sono sottovalutate e/o relegate a essere definite "false". Possiamo anche accettarle come "non reali", ma di sicuro vengono avvertite quando si ha a che fare con un sistema di riferimento non inerziale. E, analogamente, un sistema non inerziale non è assolutamente di importanza secondaria rispetto a uno inerziale. La nostra stessa Terra, luogo in cui avvengono la maggior parte dei normali fenomeni di meccanica, è un sistema non inerziale. Molte volte possiamo anche trascurare questo fatto, ma non certo quando si vuole parlare della forza di Coriolis.
In parole molto povere, per descrivere un certo moto in un sistema non inerziale, è necessario introdurre delle forze aggiuntive. Il caso, forse, più classico è quello della forza centrifuga, nel caso del moto circolare uniforme. Esso, visto da un sistema inerziale esterno, è un moto soggetto a una sola forza reale, quella centripeta. Tuttavia, chi lo sta effettuando (una pallina legata a un filo o un pianeta attorno a una stella), e si considera fermo, non può fare a meno di introdurre una forza uguale a contraria in grado di mantenerlo in quiete. E questa forza "apparente" è proprio la centrifuga, l'unica veramente avvertita dalla pallina che ruota velocemente, ma che è sicura di stare ferma.
A parte piccole polemiche sul modo di definire certi effetti che per alcuni sono reali, ma che non lo sono per altri, è molto meglio, prima di divertirci con la forza di Coriolis (ne vedremo e ne faremo delle belle...) parlare con una certa serietà e precisione dei moti relativi di due sistemi di riferimento. In tal modo capiremo meglio la nascita delle forze fittizie e potremo descrivere in termini matematici la forza di Coriolis, insieme a sua sorella, quasi gemella, la forza centrifuga. Un po' di matematica abbastanza semplice, che presuppone la conoscenza delle operazioni vettoriali e delle derivate... niente di più.
Moti relativi
1. Posizione e velocità
Nella Fig.1, disegniamo due sistemi di riferimento cartesiani, con origine in O e O’. Possiamo anche partire con gli assi paralleli tra loro.
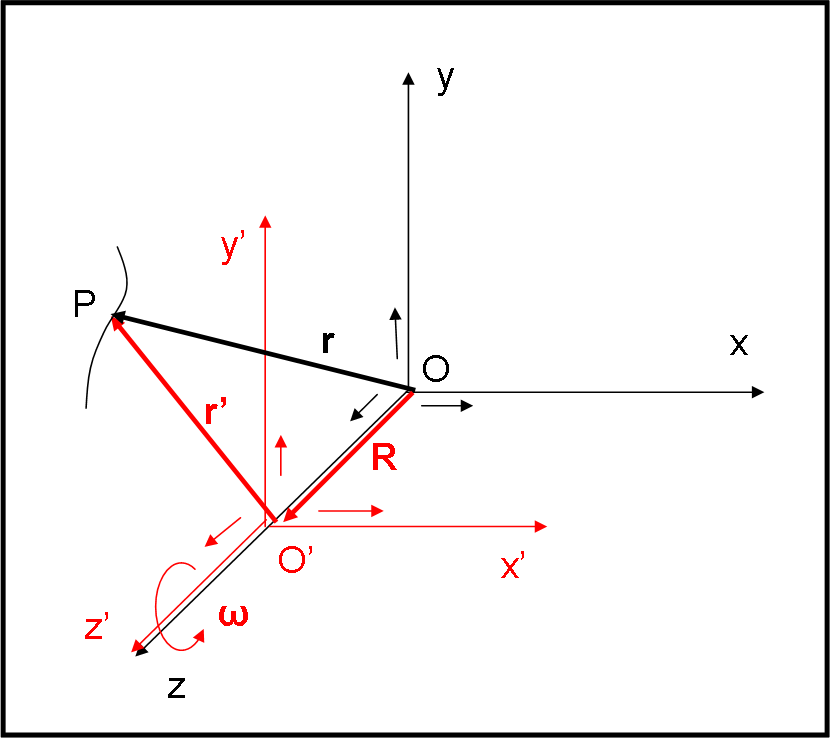
S(Oxyz) è il sistema fisso, mentre S’(O’x’y’z’) è il sistema in movimento. Consideriamo un punto P che descrive la sua traiettoria e indichiamo la sua posizione con:
r = OP
r’ = O’P
mentre la distanza tra le origini é:
R = OO’
Risulta subito (somma vettoriale):
r = R + r’ …. (1)
Facciamo prima il caso più semplice, ossia i due sistemi traslano soltanto uno rispetto all’altro. Ciò non vuol dire, però, che O’ non possa accelerare rispetto a O, ossia che la sua velocità non sia variabile. Per adesso consideriamo il caso che trasli con velocità costante.
Possiamo derivare la (1) rispetto al tempo per trovare la formula che lega le velocità.
Nel caso di pura traslazione i versori unitari degli assi (freccette nere e rosse) restano quelli che sono (in modulo, direzione e verso), ossia coincidono per entrambi i sistemi. Ciò comporta una derivata semplicissima:
dr/dt = dR/dt + dr’/dt …. (2)
v = V + v’ …. (3)
Perché? Facile a provarsi dato che per un vettore s qualsiasi di versore u (costante per traslazione) si ha:
s = s u
derivando:
ds/dt = dsu/dt = uds/dt + sdu/dt = uds/dt = uv = v …. (4)
du/dt = 0, ovviamente, dato che il versore è rimasto sempre uguale, come modulo, direzione e verso.
Se il moto, invece, è anche rotatorio, le cose si complicano dato che la derivata di un versore u (è ancora di modulo unitario, ma cambia direzione e verso) è un nuovo versore perpendicolare al primo. In particolare si dimostra che:
du/dt = ω Λ u …. (5)
Dove ω è il vettore velocità angolare (regola della mano destra, ricordate…).
Per ottenere questa semplice relazione, basta dimostrare che la derivata di un versore (non costante in direzione e verso) è sempre un versore (unitario come modulo) ma con direzione perpendicolare al primo.
Facciamo il prodotto scalare di due versori ortogonali:
(u X u) = u2 = costante
d(u x u)/dt = d(u2)/dt = 0
ma la derivata si può anche scrivere:
d(u x u)/dt = u x du/dt + u x du/dt = 2 u x du/dt
Tuttavia, sappiamo che la derivata deve essere uguale a ZERO, da cui segue che
2 u x du/dt = 0
Ossia:
u x du/dt = 0
Ma se il prodotto scalare di due versori di modulo costate è uguale a zero essi devono essere perpendicolari. Ossia, se la rotazione (ω) avviene attorno a un’asse perpendicolare a entrambi si ha proprio che du/dt può essere scritto come la (5):
du/dt = ω Λ u
La (5) diventa, per un vettore generico s di versore u:
ds/dt = d(su)/dt = uds/dt + sdu/dt = uds/dt + sω Λ u = u v + ω Λ su = v + ω Λ s …. (6)
Riprendiamo allora la (2):
dr/dt = dR/dt + dr’/dt
Tenendo conto della (6), si ottiene:
v = V + v’ + ω Λ r’ …. (7)
Riflettiamoci un attimo, confrontando la (7) con (3).
v’ è la velocità del punto P nel sistema di riferimento S’.
V è la velocità dell’origine O’ di S’ rispetto all’origine O di S.
v è la velocità del punto P nel sistema di riferimento S.
Che cosa differenzia le due velocità v e v’? Un termine che dipende solo dalla traslazione e rotazione del sistema S’, ossia non dipende assolutamente dal moto del punto P. Questo concetto è fondamentale, anche se sembra estremamente ovvio.
Questo termine possiamo chiamarlo velocità di trascinamento vT ed è dato da:
vT = V + ω Λ r’
In parole molto semplici possiamo dire che questa è la velocità che avrebbe in S un punto fermo in S’, trascinato dal moto di S’. Infatti, inserendo v’ = 0 nella (7), la v diventa proprio vT.
La (7), ovviamente, si trasforma nella (3) se non vi è rotazione. Ma, ancora più importante per noi, la (7) diventa:
v = v’ + ω Λ r’ …. (8)
se O coincide con O’ e non vi è nessuna traslazione. In poche parole stiamo lavorando con due sistemi, in cui uno si muove di moto soltanto rotatorio rispetto all’altro.
Diciamo un’altra ovvietà, che è, comunque, molto interessante…
Consideriamo nuovamente un punto P fisso rispetto a S’. Cosa vediamo da S? Beh… semplicissimo. La v’ si annulla (il punto è fermo in S’) e, quindi, la v è uguale solo al termine di trascinamento ω Λ r’. Facciamoci aiutare dalla Fig. 2 per vedere cosa significa tutto ciò…
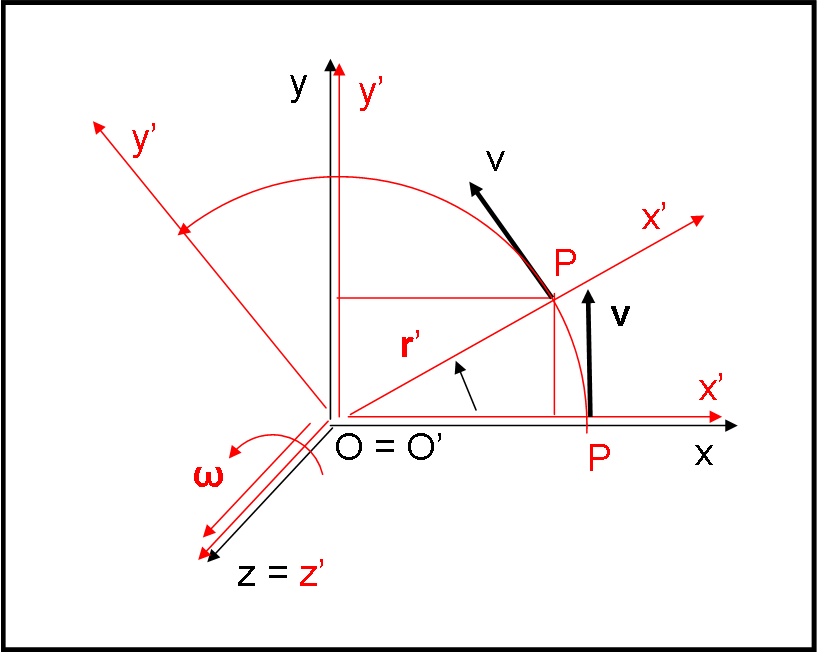
O coincide con O’ (nessuna traslazione, per cui possiamo anche fare coincidere le origini). Il sistema S’ ruota attorno all’asse z con velocità angolare costante (vettore ω). La distanza r’ rimane costante (il punto P è fisso nel sistema S’: ad esempio, possiamo metterlo sull’asse x’). Abbiamo due vettori costanti in modulo e quindi deve essere costate in modulo anche il loro prodotto vettoriale, che altro non è che la velocità v di P nel sistema S.
Tuttavia, utilizzando la regola della mano destra possiamo facilmente vedere che il vettore v cambia continuamente direzione nel sistema S, dato che lo fa anche P. Insomma, O non può che dire che P si muove di moto circolare uniforme nel piano (x,y), e che v è la sua velocità tangenziale!
2. Accelerazione
Riprendiamo la relazione che esiste tra le velocità di un sistema rotante rispetto a uno fisso (8).
v = v’ + ω Λ r’
Il prossimo passo è quello di trovare la relazione che esiste tra le accelerazioni
Nessun problema a derivare v. Essa vale a = dv/dt.
La derivata di v’ deve invece tener conto della (6) dato che il sistema sta ruotando, ossia:
dv’/dt = a’ + ω Λ v’
Ci resta ancora da derivare il prodotto vettoriale ω Λ r’
Esso vale, ovviamente:
d(ω Λ r’)/dt = dω/dt Λ r’ + ω Λ dr’/dt
Mettendo tutto assieme, si ottiene:
a = a’ + ω Λ v’ + dω/dt Λ r’ + ω Λ dr’/dt …. (9)
Sappiamo, però dalla (6) che:
dr’/dt = v’ + ω Λ r’
Sostituendo questa relazione nella (9), si ha:
a = a’ + ω Λ v’ + dω/dt Λ r’ + ω Λ (v’ + ωΛr’)
a = a’ + ω Λ v’ + dω/dt Λ r’ + ω Λ v’ + ω Λ (ωΛr’)
a = a’ + dω/dt Λ r’ + 2ω Λ v’ + ω Λ (ω Λ r’) …. (10)
Dove a’ è l’accelerazione nel sistema di riferimento rotante. Mettendola in evidenza, si ha:
a’ = a - dω/dt Λ r’ - 2ω Λ v’ - ω Λ (ω Λ r’) …. (11)
Assumendo (per noi basta e avanza) che ω sia costante, si annulla il termine che contiene la derivata di ω:
a’ = a - 2ω Λ v’ - ω Λ (ω Λ r’) …. (12)
Questa formula è fondamentale. Ci dice una cosa che ben conosciamo, ma che abbiamo ricavato solo attraverso il calcolo delle velocità e accelerazioni relative, in due sistemi di riferimento NON INERZIALI.
Nel sistema rotante, all’accelerazione esistente nel sistema fisso, per potere applicare le leggi della dinamica, è necessario introdurre due accelerazioni particolari: una è proprio l’accelerazione centrifuga, ossia il termine -ω Λ (ω Λ r’). Infatti, se v’ fosse uguale a zero (il punto fosse fisso nel sistema di riferimento rotante) avremmo che questa è l’unica accelerazione che bisogna aggiungere all’accelerazione esistente nel sistema fisso. Quest'ultima accelerazione è quella centripeta e, quindi, il termine - ω Λ (ωΛr’) è proprio quella che tiene il punto fisso nel suo sistema rotante.
Se, però, v’ non è uguale a zero (ossia il punto si sposta anche nel sistema di riferimento), deve entrare in ballo anche un’accelerazione aggiuntiva (che non viene annullata) e che è sempre perpendicolare alla direzione del moto. Questa non è altro che l’accelerazione di Coriolis, libera di agire e di essere ben visibile.
Moltiplicando tutte le grandezze per la massa M del corpo in movimento, si ottiene la relazione tra le forze vere e le forze fittizie, ossia quelle legate ai termini che fanno differire le due accelerazioni.
Fino a qui abbiamo eseguito alcune semplificazioni, una fra tutte quella di far coincidere le origini dei due sistemi. In realtà, ci saremmo dovuti “portare dietro” un altro termine aggiuntivo, ma estremamente facile da tenere in conto. OO’ avrebbe avuto una velocità V e un’accelerazione A.
Come riepilogo, scriviamo, allora, le tre relazioni, complete di traslazione, ma con velocità angolare costante:
r = R + r’
v = V + v’ + ωΛr’
a = A + a’ + 2ω Λ v’ + ω Λ (ωΛr’) …. (13)
A seconda delle ipotesi di partenza sul moto di un sistema rispetto all’altro, le tre relazioni si semplificano di conseguenza.
Prendiamo il caso più classico: Le origini non coincidono, ossia OO’ è diverso da zero. Ancora più importante il fatto che O’ si muova rispetto a O con velocità costante V. Il sistema mantiene gli stessi versori, ossia non vi è rotazione. Ne segue che ω = 0. Le relazioni diventano:
r = R + r’
v = V + v’
a = a’
Esattamente le condizioni che definiscono due sistemi inerziali.
Se, invece, la velocità di O’ fosse variabile, avremmo:
r = R + r’
v = V + v’
a = A + a’
E via dicendo …
Per lo studio dei sistemi rotanti senza traslazione e con O = O’(quelli che c’interessano per vedere gli effetti della forza di Coriolis) possiamo tornare alle relazioni che abbiamo ricavato nell’articolo:
r = r’
v = v’ + ω Λ r’
a = a’ + 2ω Λ v’ + ω Λ (ω Λ r’) .... (14)
Notiamo un fatto molto importante: la forza di Coriolis non è mai sola, ma è sempre accompagnata da quella centrifuga, mentre non è vero il viceversa. Inoltre, ribadiamolo ancora, la forza di Coriolis nasce solo quando si ha un movimento del corpo in uno dei due sistemi di riferimento. Tuttavia, a seconda che si muova in quello rotante o in quello fisso, gli effetti sono diversi… cosa che spesso viene male interpretata…
Le relazioni precedenti porterebbero alle equazioni del moto, come quelle di pura traslazione. Noi, però, ci limiteremo a descrivere i vari effetti graficamente, sapendo ormai bene quali forze agiscono, siano esse vere o “fittizie”.
La trattazione della forza di Coriolis e dei moti relativi tra due sistemi potrebbe anche finire qui. Tuttavia, gli effetti delle due forze fittizie (soprattutto quella di Coriolis) sono tanti e tali da meritare di passare un po' di tempo con loro, limitando il tutto a costruzioni puramente geometriche
Sistemi rotanti
Semplifichiamo il problema da risolvere, considerando due sistemi di riferimento, aventi la stessa origine, e manteniamo tesa un corda fissata all’origine, che porta all’altra estremità una palla di ferro. In altre parole, simuliamo un lanciatore di martello. Chi è fuori dalla pedana, nello stadio, vede ruotare la palla, tenuta a distanza costante dal centro, attraverso la corda che deve rimanere ben tesa. La sfera, invece, si sente sempre ferma nel suo sistema rotante. Possiamo dire tranquillamente che per chi è nello stadio esiste solo una forza centripeta (la corda) che evita che la palla scappi verso il pubblico. E’ lei che costringe la palla a ruotare invece di mantenere il suo moto rettilineo uniforme. La palla, invece, si sente ferma e SENTE, anche molto bene, una forza che la porterebbe verso l’esterno, in direzione opposta a quella del centro. Se non ci fosse la corda che la tiene ferma seguirebbe questa forza estremamente violenta (dipende molto dalla rotazione impartita). In parole semplici: lo spettatore dello stadio vede la palla ruotare, mentre la palla vede corda e se stessa sempre ferme.
Cosa succede se tagliassimo la corda! No, no, non andarcene via, ma tagliare veramente la corda che tiene unita la palla con l’origine degli assi. A questo punto ci chiediamo:
1. Che traiettoria segue la palla se il fenomeno è visto dal sistema “stadio”, ossia dal sistema che possiamo considerare fermo?
2. Che traiettoria segue la palla se il fenomeno è visto dal sistema rotante (che continua a ruotare anche se la corda viene tagliata)?
La situazione è quella rappresentata in Fig. 3.
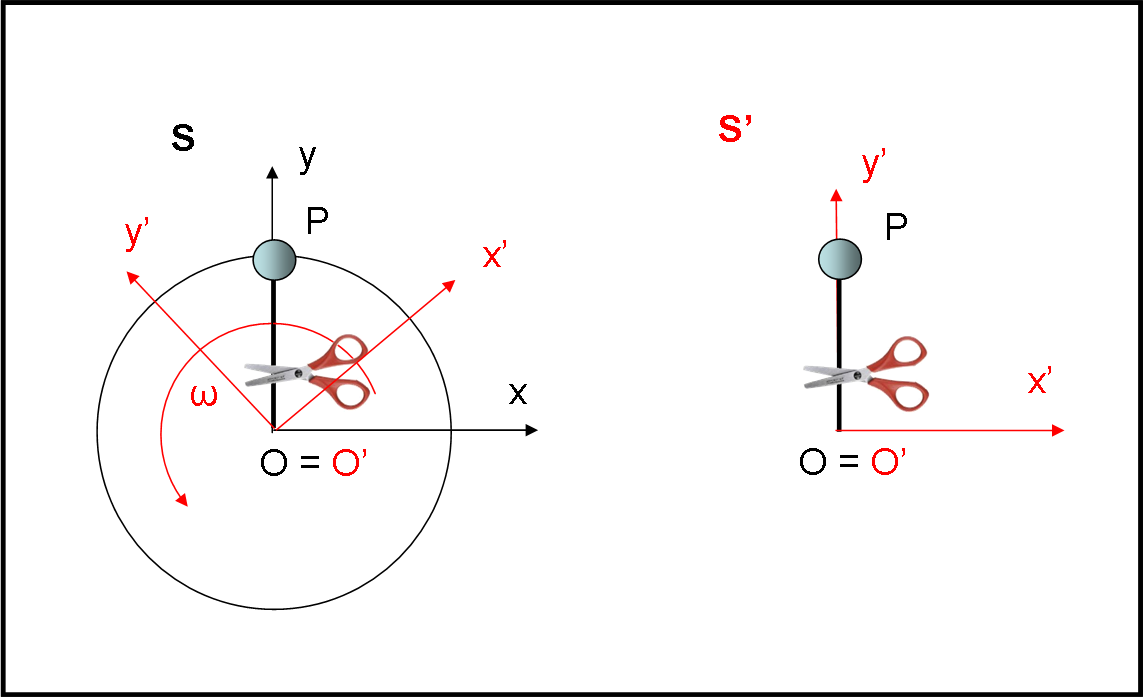
Abbiamo due sistemi di riferimento: uno nero (fermo) e uno rosso (rotante con velocità angolare ω). La palla P è solidale, ovviamente, con il sistema rotante. Uno ha assi x, y e z, l’altro x’, y’ e z’. Tuttavia, l’asse z coincide con z’, dato che rappresenta l’asse di rotazione. Possiamo immaginarlo diretto verso di noi, perpendicolare al foglio e quindi evitare di disegnarlo. Limitiamoci al piano x,y che coincide con il piano x’,y’ (il piano, non gli assi!). Per rispondere alla prima domanda dobbiamo riferire il moto agli assi immobili x e y. Per rispondere alla seconda domanda dobbiamo riferire il moto agli assi x’ e y’ immaginati fermi.
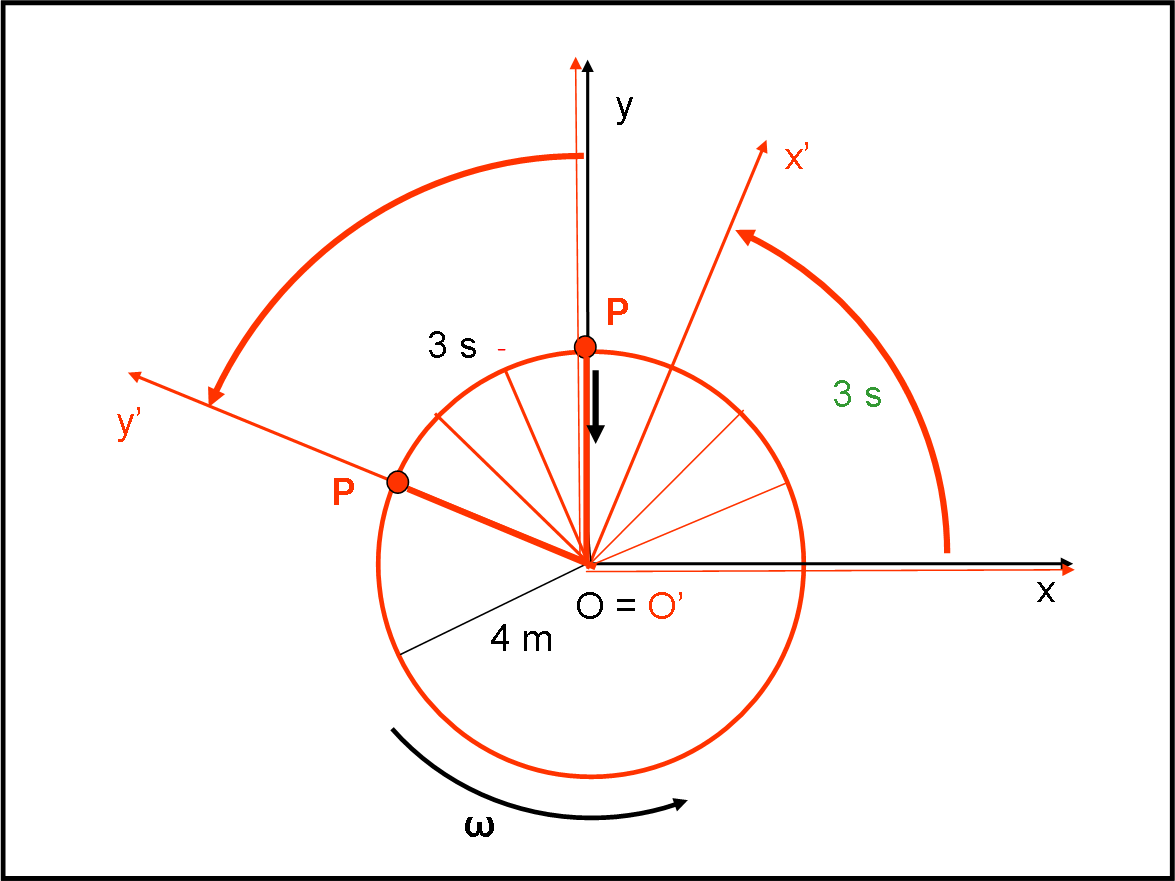
Per rendere più quantitativo il nostro problemino, diamo dei valori numerici. Il minimo indispensabile!
Raggio OP = O’P = 4 metri
Periodo di rotazione del sistema (e quindi anche della palla prima del taglio della corda) = 16 secondi (notate che la scelta non è casuale, ma permette di disegnare al meglio momenti diversi della rotazione).
La descrizione del fenomeno può essere fatta per punti e poi cercare di unirli nel modo migliore, sempre che ve ne sia bisogno…
Ricordiamo ancora: abbiamo escluso la forza di gravità che tenderebbe a far cadere al suolo la palla in tempi piuttosto brevi.
Cominciamo col ripetere le condizioni di partenza, continuando a segnare in nero il sistema fermo e in rosso quello rotante. La palla è tenuta dalla corda e ruota attorno all’origine O = O’ con velocità angolare ω. Palla e corda sono disegnate in rosso, dato che appartengono (ossia sono solidali) con il sistema rotante. Come ben sappiamo il tutto capita per merito di una sola forza reale (ossia esistente nel sistema inerziale): la forza centripeta, rappresentata dalla corda che non fa scappare la palla e le permette di mantenere la sua velocità costante (in modulo). Così pensa l’osservatore solidale con il sistema fermo: lui vede corda e palla ruotare con grande regolarità (Fig. 4).
Ben diversa è la situazione per l’osservatore solidale con il sistema rotante. Per lui la palla e la corda sono sempre ferme (Fig. 5).
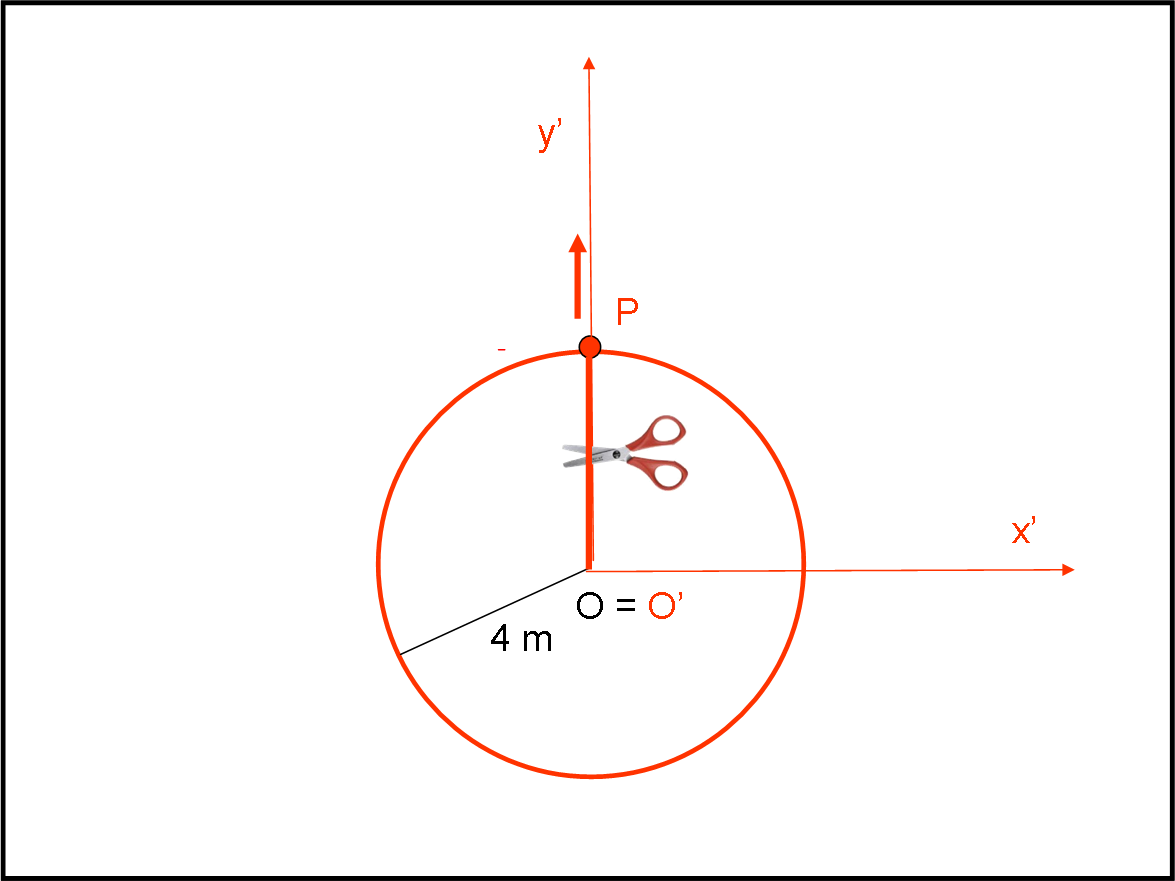
Se si mettesse sopra la palla sentirebbe una forza trascinarlo verso l’esterno in senso radiale (forza centrifuga), ma la corda riesce a non farlo scappare in quella direzione. Un gioco di tira e molla che si svolge in posizione statica, senza avvertire nessuna rotazione. Caso mai è tutto lo stadio esterno che sembra ruotare con velocità angolare - ω, ossia in senso orario. Ma non pensiamo a questo e torniamo alla nostra pedana. E’ giunto il momento di tagliare la corda!
L’osservatore solidale con il sistema rotante è pronto a scommettere che la palla se ne vada in senso radiale, seguendo quella forza che la spingeva verso l’esterno. Subito dopo il taglio, l’impressione è proprio quella, ma poi…
Per comprendere meglio cosa succede, portiamoci nello stadio e guardiamo le cose da un sistema inerziale, dove le leggi di Newton si applicano senza problemi. Tagliando la corda, viene a mancare l’unica forza che trattiene la palla e la costringe a ruotare (forza centripeta). La palla non può che seguire la legge di Newton e andarsene lungo la direzione tangente alla circonferenza, nella direzione della velocità istantanea (Fig. 6).
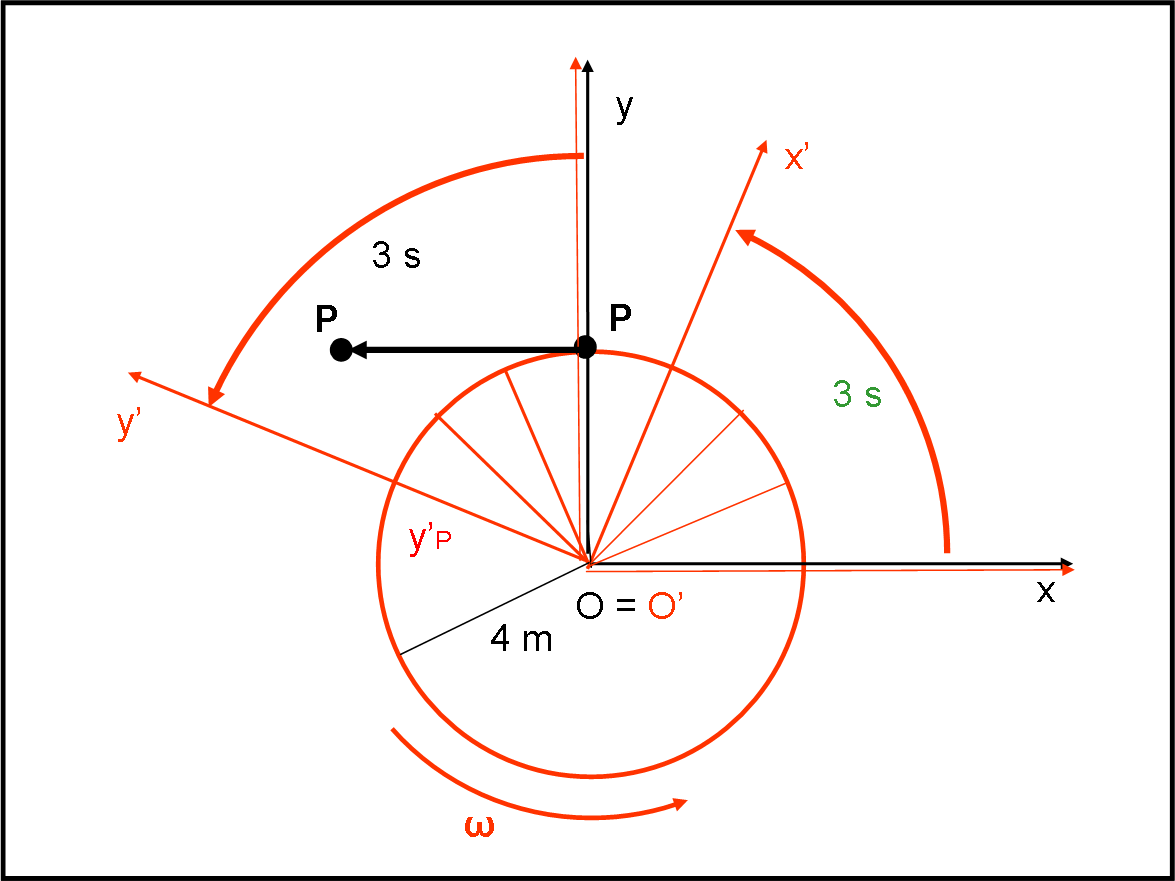
Attenzione: questa velocità si mantiene e rimane costante, dato che non esistono più forze a darle fastidio. A questo punto la palla P diventa nera dato che appartiene al sistema inerziale dello stadio. Il suo moto è rettilineo e uniforme.
Torniamo al sistema rotante. Come vede la traiettoria della palla P? Facile a costruirsi. Facciamo ruotare gli assi rossi di un certo angolo (freccia curva rossa) e vediamo quali sono le coordinate x’ e y’ della palla P rispetto agli assi rotanti rossi. Basta tracciare le perpendicolari agli assi x’ e y’. Queste coordinate le abbiamo disegnate in verde (Fig. 7).
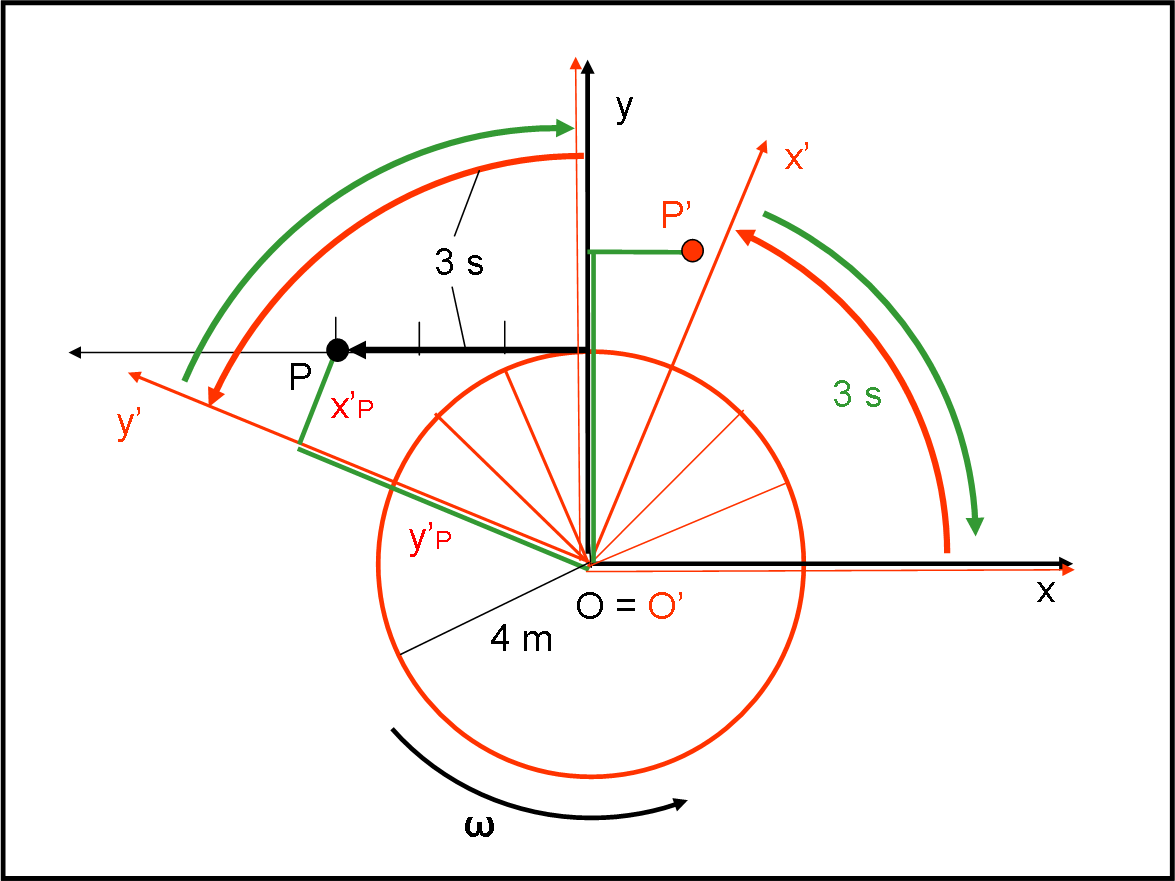
Il sistema, però, si considera fermo e, perciò, conviene riportare l’asse y’ nella posizione iniziale, utilizzando la rotazione inversa disegnata in verde. Troveremo il punto P’, che indica la posizione della palla P nel sistema rotante (possiamo disegnarla in rosso).
Per disegnare tutta la traiettoria, bisogna calcolare di quanto si sposta la palla P lungo la traiettoria rettilinea (verso sinistra), in un secondo. Nello stesso tempo, gli assi rossi ruotano di un certo angolo.
Sappiamo che il periodo T è di 16 secondi, così come sappiamo che il raggio R (lunghezza della corda) è di 4 metri.
Abbiamo subito il valore della velocità angolare:
ω = 2π/T = 6.28/16 rad/s
La velocità tangenziale, ossia la velocità costante della palla (moto circolare uniforme) è data da:
v = ω R = (6.28·4)/16 = 6.28/4 = 1.57 m/s
Spostando la palla del valore di 1,57 m sulla linea orizzontale verso sinistra, si devono ruotare gli assi rossi di 22.5°, proprio l’angolo descritto in un secondo dal sistema rotante: 360/16 = 22.5°.
Ottenuto il primo punto P’, si ruota il sistema rosso di un altro angolo di 22.5°, portandolo a 45° rispetto alle condizioni iniziali (y’ = y). Si trovano le nuove coordinate e si ripete l’operazione eseguita in Fig. 7. E via dicendo, stando bene attenti alle coordinate del nuovo punto P rispetto agli assi rossi ruotati dell’angolo corrispondente. Alla fine si ottiene, in un periodo di tempo di 8 secondi (mezzo periodo) la curva di Fig. 8.
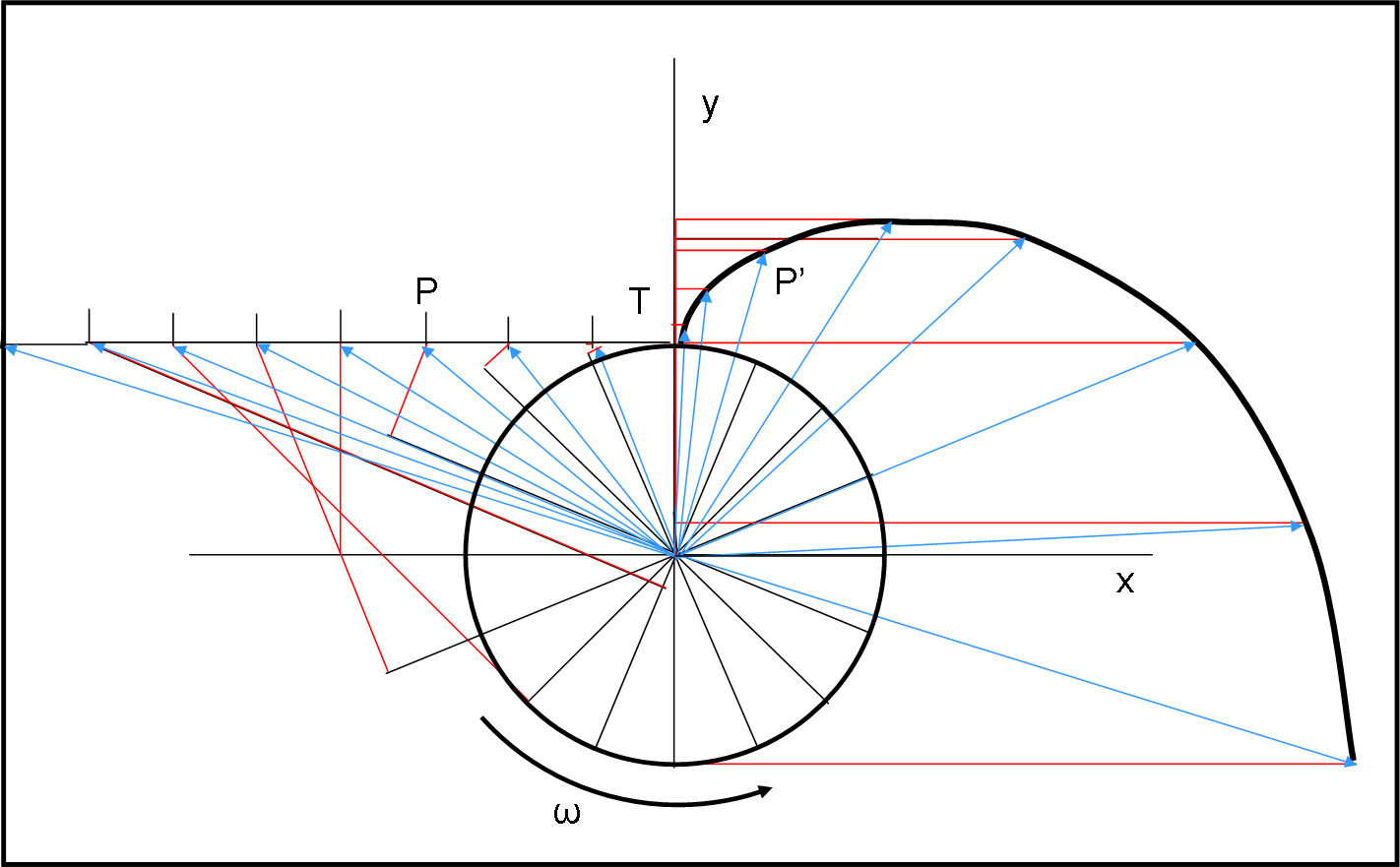
Mamma mia! Altro che scappare lungo la direzione della forza centrifuga… otteniamo una curva che si allarga sempre di più verso destra. Una spirale, ma c’interessa poco il suo nome matematico, dato che vogliamo soprattutto capire come questa strana situazione possa capitare.
Innanzitutto ci deve essere una qualche forza “aggiuntiva” che tende a far curvare la traiettoria, rispetto a quella rettilinea che sembrava essere indicata dalla forza centrifuga. Due forze che agiscono insieme e che non esistono nel sistema inerziale.
Cerchiamo di capire la faccenda in modo molto qualitativo, per adesso…
Consideriamo le frecce azzurre. Per ogni posizione P della palla esse indicano di quanto si è spostata la palla in senso radiale. In altre parole, illustrano come sembra muoversi a causa della sola forza centrifuga. Fosse stata da sola, questa forza avrebbe fatto spostare, come immaginato in un primo momento, la palla P lungo l’asse verticale (l’asse y’ iniziale, considerato fermo). E invece, vi è un netto e chiaro spostamento verso destra… spostamento curvilineo, come già detto. Niente da fare, abbiamo di fronte una nuova forza! Questa forza è proprio la forza di Coriolis e nasce quando si ha un sistema rotante e un punto P che si muove con una certa velocità. Proprio il nostro caso: noi abbiamo la rotazione, ma anche lo spostamento di P lungo la retta TP.
Tenendo sempre presente i semplici calcoli eseguiti nella descrizione matematica data all'inizio, si può facilmente ottenere la velocità istantanea della palla P’ lungo la strana traiettoria e anche le forze che agiscono su di lei. Ci arriveremo…
La forza di Coriolis, la famosa forza di Coriolis, che sulla nostra Terra tutto fa meno che far girare l’acqua nei rubinetti (o nei bicchieri di vino...). Attenzione, però, a non confondersi. Nel caso trattato finora, ciò che vedrebbe un alieno dal di fuori (sistema inerziale), sarebbe una velocità rettilinea e uniforme della palla. D'altra parte, notando la bella curva ottenuta, sembrerebbe ovvio passare alle curve spiraleggianti dei cicloni e anticicloni terrestri. Potremmo dire, frettolosamente, che i cicloni nascono direttamente dalla forza di Coriolis e che quindi sono visibili nel sistema terrestre. Un po' di calma, è necessario studiare la faccenda con maggiore attenzione... anche a costo di essere ripetitivi. In ogni modo c'è molto spazio per divertirsi.
Prendiamo dimestichezza con i moti relativi (e con la Terra)
Un piccolo quiz ci introduce, prendendoci per mano, verso problemi di ben altra importanza, che tratteremo parlando di Coriolis e di Foucault. Quando si ha voglia di pensare, si scoprono, a volte, fenomeni inaspettati…
Ogni giorno si parla di un nuovo pianeta extraterrestre che dovrebbe ospitare più vita di quello di prima. Mi sa che, alla fine, troveremo una Terra proprio uguale alla nostra (come in Fantasia…). Tuttavia, queste ripetute notizie, sempre “pizzicate” dai media, stanno facendo il giro del mondo e … non solo.
Insomma, alla fine, gli alieni se ne sono accorti e sono venuti a trovarci, chissà con quali intenzioni bellicose. E, guarda caso, hanno proprio adocchiato l’Italia (forse perché siamo i più alieni di tutti?). I vari moduli spaziali hanno individuato un’enorme astronave in rotta verso il nostro pianeta ed esattamente verso il nostro Bel Paese. Accidenti!
Gli scienziati fanno subito i calcoli della traiettoria dell’astronave. Si tira un sospiro di sollievo: essa è diretta verso il Polo Nord e continuerà sempre di moto rettilineo uniforme. La sua velocità non è poi troppo alta (che stiano solo facendo un po’ di turismo spaziale?) e in dodici ore attraverseranno tutta la Terra e continueranno nello Spazio verso un’altra meta (si spera…).
Tutto bene? Nemmeno per sogno! In Italia, dopo un primo momento di speranza, la faccenda sembra prendere una piega ben diversa. L’astronave ha cambiato rotta! Sta tornando indietro e punta veramente verso di noi… Forse gli alieni hanno deciso di rivoluzionare il nostro sistema politico e fare piazza pulita dell’intera classe dirigente?
No, purtroppo no… il pericolo rientra e i nostri governanti possono staccare le mani dalle loro poltrone che tenevano ben strette: nessuno gliele porterà via…
Forza, aiutatemi a capire che cosa è successo veramente?
In particolare le domande sono due:
1. Qual è la traiettoria che un osservatore italiano vede compiere all'astronave
2. Quale sarebbe la traiettoria, sempre vista dall'Italia, se l'astronave avesse una velocità dimezzata (ossia impiegasse 24 ore ad attraversare la Terra)?
La spiegazione è, praticamente, simile nella sua trattazione a quella del taglio della corda, ma è meglio richiamarla per essere pronti ad andare verso costruzioni leggermente più difficili…
Se nel sistema di riferimento esterno, fisso, tutto torna molto bene (basta mettersi in un punto esterno e guardare cosa succede), è molto più complicato, mentalmente, immaginarsi fermo in un sistema rotante. E’ vero che lo proviamo tutti i giorni, sia in macchina che su una giostra, ma noi SAPPIAMO di stare ruotando e molte cose che capitano vengono travisate o confuse. Dobbiamo fare lo sforzo mentale di sentirci veramente FERMI, anche quando ci si muove!
La cosa migliore da fare, per rappresentare ciò che si vede in un sistema rotante, è bloccare le condizioni di partenza e riferire tutto ciò che si osserva in quelle condizioni. In tal modo l’osservatore si considera fermo qualsiasi cosa faccia il suo sistema di riferimento.
Prima, risolviamo il piccolo mistero con il solo ragionamento e poi lo descriveremo con un disegno riferito al sistema rotante. Utilizziamo lo schema di Fig. 9.
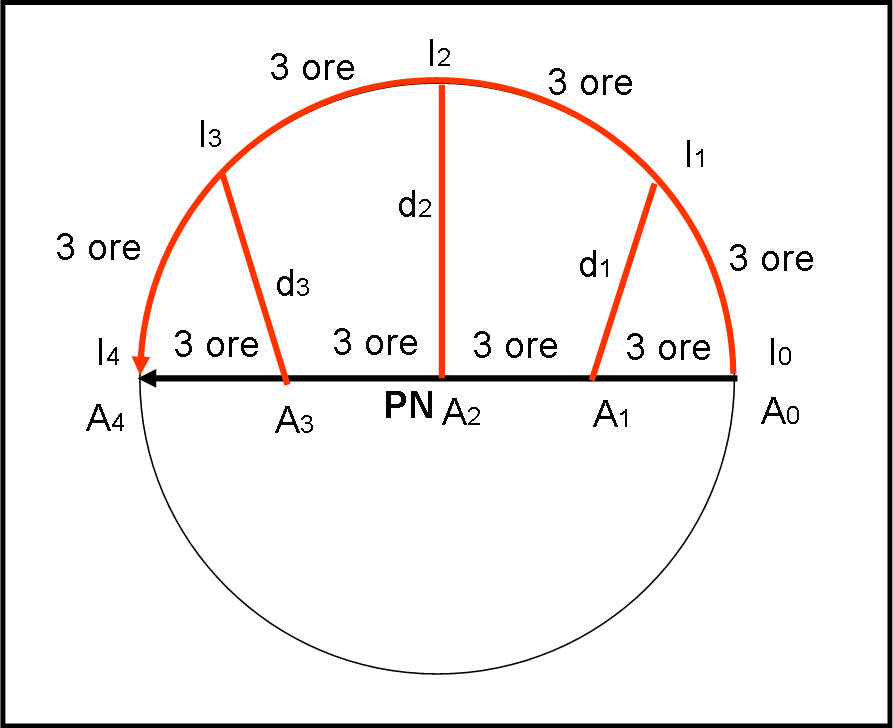
Continuiamo a proiettare tutto nel piano perpendicolare al Polo Nord (notiamo come il sistema rotante del lancio del martello sia ora la proiezione della Terra vista dal polo). In un certo istante t0 l’astronave A0 e l’Italia I0 si trovano proprio una sopra l’altra: a parte l’altezza (che nella proiezione non si vede), la loro distanza è esattamente zero. Facciamo passare tre ore (un quarto del percorso di entrambi i “contendenti”) e siamo nelle condizioni I1 e A1. Beh… è indubbio che la distanza d1 non sia più zero e che l’astronave si stia allontanando dal nostro Bel Paese.
La situazione diventa ancora più rilassante dopo altre tre ore: l’astronave è in A2 e la sua distanza, sul piano del foglio, è diventata proprio il raggio della circonferenza su cui sta girando l’Italia (il suo cerchio di latitudine), che si trova in I2. A questo punto, però, le cose cambiano…
Dopo altre tre ore l’Italia si viene a trovare in I3, mentre l’astronave in A3. Accidenti, la distanza è tornata come quando eravamo in I1, ossia sta diminuendo. La catastrofe (se così vogliamo chiamarla) capita quando l’Italia arriva in I4. Sono passate dodici ore dalla partenza, lo stesso tempo che l’astronave ha impiegato per arrivare in A4. Siamo di nuovo nelle condizioni di partenza (I0, A0): l’astronave è tornata sopra la nostra testa!
Noi, italiani, non ci siamo accorti di aver fatto una mezza circonferenza nello stesso tempo in cui l’astronave ha compiuto la sua traversata , quindi, ci siamo considerati FERMI. In tale rappresentazione l’astronave è sembrata proprio allontanarsi per poi tornare indietro. E’ un po’ come se avessimo sparato con una pistola e poi, facendo un altro percorso, fossimo arrivati a incontrare il proiettile ancora in volo: un suicidio molto particolare…
Torniamo ai nostri sistemi e applichiamo il metodo consigliato precedentemente, per disegnare ciò che si vede in un sistema rotante. In altre parole la congiungente Italia-Polo Nord deve rimanere sempre la stessa. Una costruzione molto simile (e anche più facile) di quella necessaria a descrivere la traiettoria di una palla rotante a cui abbiamo tagliato la corda che la faceva girare attorno a un centro fisso. Attraverso questa descrizione, sarà ancora più semplice tornare al lancio del martello e capire le varie manovre che avevamo eseguito.
Utilizziamo la Fig. 10.
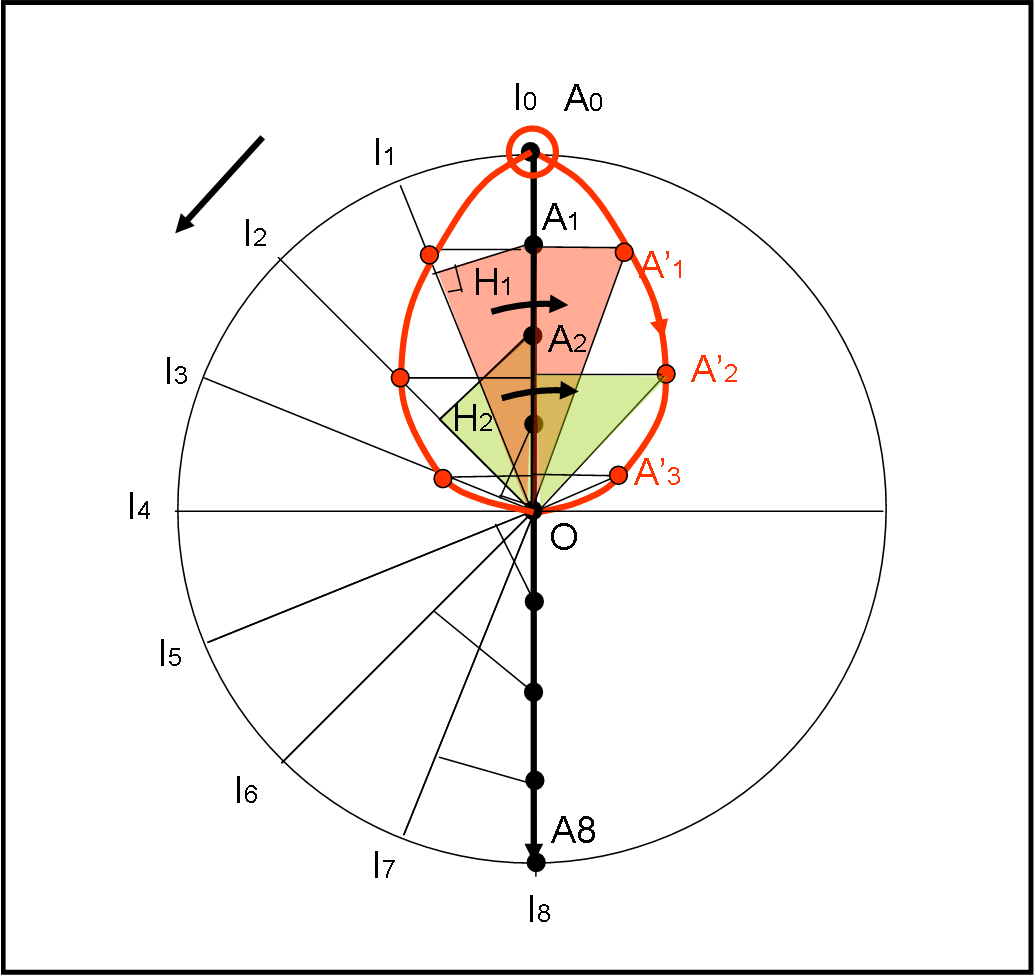
Per costruire meglio la traiettoria descritta dall’astronave nel sistema rotante dell’Italia, utilizziamo intervalli di tempo (e quindi angolari) minori di tre ore, ad esempio un’ora e mezza (ossia 180°/8 = 22.5°). In altre parole, abbiamo diviso il viaggio dell’astronave in 8 intervalli (punti neri), così come quello dell’Italia.
Vediamoli nel sistema fisso di un alieno, dove abbiamo chiamato O il Polo Nord (l’unico punto che resta fermo in entrambi i sistemi). Ogni intervallo angolare percorso dall’Italia va da 1 a 8, così come le posizioni dell’astronave. Come si vede bene (da un sistema fisso esterno), l’Italia, dopo 12 ore (I8), coincide con l’astronave nel suo punto finale A8. Avremmo già risolto il problema di partenza (si sono di nuovo incontrate!), ma a noi interessa, adesso, vedere come appare la traiettoria dell’astronave dall’Italia considerata ferma nel suo sistema rotante. Solo così vedremo agire l’accelerazione di Coriolis…
Ne consegue che, praticamente, prima dobbiamo utilizzare la posizione relativa tra Italia e astronave nel sistema inerziale fisso e poi far coincidere il punto relativo all’Italia con quello iniziale. Se in questo caso, la faccenda è quasi ridicola, non lo sarà più per movimenti meno semplici… fidatevi!
Cominciamo a considerare l’Italia nel punto I1. Nello stesso istante l’astronave coincide con il punto A1. Cosa dobbiamo fare adesso? Considerare l’asse OI1 come nuovo asse del sistema rotante rispetto a cui riferire la posizione dell’astronave. Basta allora tracciare la perpendicolare dal punto A1 al l’asse OI1. Per riportare il tutto nelle condizioni iniziali, dobbiamo far coincidere A1 con A0 (pallino rosso grande), ossia dobbiamo far ruotare il triangolo OH1A1 verso destra fino a far coincidere A1 con A0. Ne segue che il punto A1 si sposta in A’1. Questo è il primo punto del percorso dell’astronave visto da A0, considerato fermo. Stiamo costruendo, lo ripetiamo, la traiettoria dell’astronave come viene vista dall’Italia considerata ferma e sempre coincidente con I0.
Non ci resta che proseguire con questo giochino, spostandoci nel nuovo asse OI2: Nello stesso istante l’astronave si è portata in A2. Tracciamo da A2 la perpendicolare a OI2 e otteniamo il nuovo triangolo rettangolo verde IH2P2. Solita rotazione verso destra fino a che I2 coincida con I0 e il gioco è fatto: abbiamo trovato A’2. Per non pasticciare troppo la figura continuiamo a ripetere il meccanismo fino ad arrivare nel punto O, dove giunge anche l’astronave A4 e dove si posiziona anche A’4.
L’astronave continua ad andare verso il basso, mentre l’Italia continua a girare in senso antiorario. Poco male, continuiamo a tracciare le perpendicolari dai punti relativi all’astronave agli assi rotanti che congiungono il centro con l’Italia. Ci accorgiamo subito che la faccenda è perfettamente simmetrica a prima e che, riportando gli assi sopra quello iniziale I0O, si ottiene una curva simmetrica a quella dell’andata, rispetto all’asse iniziale Italia-Polo Nord (I0O).
Eh sì, è proprio vero… L’astronave torna verso l’Italia (che si considera FERMA), descrivendo una curva (Coriolis non perdona) molto interessante e forse inaspettata.
Teniamo conto di una semplificazione che abbiamo fatto: abbiamo considerato la distanza, tra Italia e astronave, solo nel piano del foglio (come se la Terra fosse piatta), ma a noi interessava proprio questa distanza e quindi nessun problema per il risultato finale.
Esistono altri molti modi di agire per ottenere la curva finale. Noi abbiamo usato quello più “classico”, ossia che lavori con coordinate cartesiane (in pratica, i nostri triangoli hanno come cateti le coordinate dei punti dell’astronave rispetto a due assi che continuano a ruotare), ma potevamo anche sbizzarrirci, considerando altre coordinate.
A questo punto, direi che non vi sono più problemi teorici nel costruire nuovamente la traiettoria dell’astronave, dimezzando la sua velocità. Bisogna stare bene attenti a non confondersi e a utilizzare sempre punti e assi rotanti corrispondenti, oltre a tenere conto che le coordinate di riferimento possono diventare negative. Tuttavia, se ruotiamo nel giusto verso e della giusta “quantità”, non vi sono veri problemi: l'importante è che l'asse rotante vada a coincidere con quello di partenza, ruotando il tutto (sia a destra che a sinistra, come si preferisce e/o come risulta più immediato).
Proviamo a svolgere il nuovo “compitino”, seguendo questa trattazione molto semplice, ricordando però di mantenere fissa la congiungente Italia-Polo Nord, ossia I0O. La nostra astronave ci farà spaventare solo per poco tempo e poi tireremo un sospiro di sollievo…
La Fig. 11 riassume il risultato in modo molto rapido (aumentando i punti, la curva si costruirebbe molto meglio).
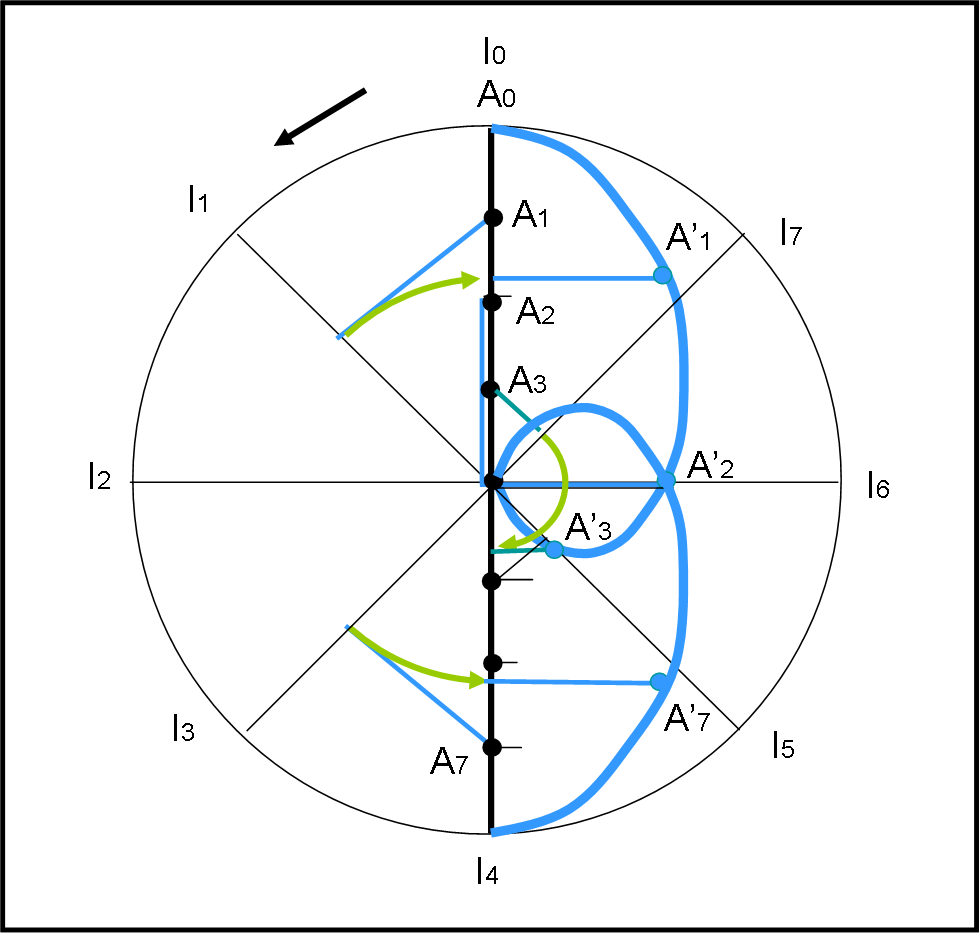
In essa ho costruito solo alcuni punti, disegnando in verde le frecce che servono a riportare l'asse rotante nella posizione originaria. Come si vede bene, dopo le 12 ore percorse dall'Italia, si può benissimo invertire il senso della freccia, dato che l'importante è tornare alle origini.
Altrettanto facile sarebbe costruire la traiettoria per un'astronave che riduce ancora di più la sua velocità (ad esempio, impiegando 36 o 48 ore ad attraversare la Terra). Roba da far "girare" la testa...
Bando agli alieni più o meno veloci (che ci hanno aiutato molto a immaginarci fissi in un sistema non inerziale e a guardare in faccia gli effetti dell'accelerazione di Coriolis), la prossima volta proseguiremo verso effetti più plateali ed evidenti.
Diciamo una banalità che, a volte, potrebbe creare qualche confusione. Cosa vedrebbe un altro osservatore esterno fermo? Sicuramente vedrebbe l'astronave andare di moto rettilineo uniforme, ma se l'astronave lasciasse cadere della polvere colorata lungo il suo viaggio, quest'ultima lascerebbe sulla superficie terrestre proprio le curve che abbiamo descritto precedentemente.
Notiamo, inoltre, un fatto importante, da non trascurare certamente. Nel caso del lancio del martello, quest'ultimo quando è stato lasciato ha conservato la velocità che aveva nel sistema rotante. Nel caso dell'astronave, quest'ultima ha solo la sua velocità di crociera, assolutamente non influenzata dal moto della Terra. Le situazioni sono decisamente differenti e le confronteremo tra poco. Prima, però, vediamo come l'intera faccenda potrebbe essere descritta geometricamente utilizzando un metodo apparentemente diverso. Un metodo che ci permette di far parlare un po' le particelle che abitano un sistema rotante e quella che ha deciso di attraversarlo (nel caso precedente i punti della Terra e l'astronave aliena).
Lo scopo vero è quello di dare a un gioco, apparentemente solo geometrico, un senso molto più fisico.
Una piattaforma parlante
Abbiamo giocato con astronavi e con palline che scappano per la tangente. Siamo riusciti a descrivere le traiettorie di questi oggetti che tutto sono meno che banali e immediate. La loro curvatura ci porta subito all’esistenza di accelerazioni (e, quindi, di forze) fittizie e, in particolar modo, a quella di Coriolis. Leggendo la parte matematica iniziale, la cosa può anche non stupire, ma vogliamo arrivarci in modo intuitivo e fisico, abbandonando, provvisoriamente, la geometria pura.
Consideriamo una normale piastra, rotante, con velocità costante. Il suo centro di rotazione sia O. Immaginiamo, adesso, una pallina P che si trovi per caso proprio sopra la piastra, ma che non la tocchi per niente (ossia non subisca attrito). Lei appartiene a un sistema inerziale, immobile e non si muove di un millimetro. Un punto fisso per il sistema inerziale, tranquillo e rilassato (l'astronave precedente fermatasi su un punto della Terra senza toccarla).
Mentre è lì che si gode il riposo, probabilmente meritato (con quella imprevedibile Cinematica non si sta mai fermi, accidenti!), gli si chiudono perfino gli occhi. Il pisolino, però, viene interrotto dalle voci che provengono dagli abitanti della piattaforma rotante. Guardando bene, infatti, la pallina nota che anch’essa è composta da tanti punti come lei, ma essi girano in modo impressionante. In particolare, vede che quelli più lontani dal centro compiono un percorso più lungo, in un certo intervallo di tempo, rispetto a quelli che sono più vicini al centro, che è l’unico punto a non muoversi per niente.
Una corsa continua per rimanere sempre tutti solidali tra loro: lo devono fare assolutamente perché la piastra resti unita. Se anche un solo punto andasse per i fatti suoi, inizierebbe una reazione a catena e la piastra si sfalderebbe completamente. Ma quello che stupisce la pallina è ciò che dicono i punti che stanno su uno stesso raggio della circonferenza. Pur faticando come pochi, essi sembrano avercela con lei, povera pallina P in cerca di pace. Essi dicono: “Hai visto quella pallina aliena? Chi glielo fa fare a correre così e sempre ruotando attorno a O. Per rimanere in quella posizione e mantenere quel moto deve subire sicuramente una forza che la attiri verso il centro. Meno male che corre come una disperata e riesce sempre a non cadere.
Lei risponde subito: “No, no, amici miei… guardate che sono io che sto ferma, mentre voi girate come dei matti. Pensavo proprio a una forza che vi tiene legati al centro, ma che riuscite a contrastare mantenendo una velocità più o meno alta a seconda della vostra distanza da O”. “Ma tu sei pazza, noi siamo fermi e non fatichiamo per niente…”. “Ne siete proprio sicuri? Non è che sentite un qualcosa che vi spinge verso l’esterno?”. “Beh… adesso che ce lo dici, è vero… ci sentiamo sempre un po’ “sbilanciati” come dici tu…”.
A quel punto, la pallina P, molto preparata in materia, tenta di spiegare la differenza tra sistemi rotanti non inerziali e sistemi inerziali. Nei primi, quando si crede di essere fermi, si è invece soggetti a una forza apparente, quella centrifuga. Sono adesso i punti della piastra a rimanere sconvolti… finché uno non prende la parola: “Ma per noi sei tu che ruoti come una disperata e quindi anche tu dovresti sentire una forza fittizia che ti spinge verso l’esterno”. Non è facile per P spiegare la differenza tra sistemi inerziali e non inerziali e i punti della piastra continuano a non capire molto bene la situazione. In altre parole, continuano a ragionare a modo loro e il punto P cerca di riprendere sonno.
Che confusione però… perfino la signora Cinematica e la sua amica Dinamica cominciano ad avere le idee confuse e decidono di eseguire un esperimento per schiarirsi le idee.
Vogliono, perciò, complicare leggermente le cose e sentire “in diretta” cosa dicono di vedere i punti della piattaforma quando la pallina P si muove di moto rettilineo uniforme. Qualsiasi punto della piattaforma può parlare a nome di tutti gli altri: non per niente sono tutti solidali tra loro, a causa di forze veramente misteriose che abbracciano gli atomi e non solo. Inoltre, sentendosi fermi, possono chiedere aiuto a tutti i punti che vogliono.
La pallina P viene spostato in O, dove in pratica continua a stare ferma, anche se gira su se stessa. Poi viene sollevata (meno male) e torna ad appartenere al sistema inerziale fermo, esterno alla piastra.
Per i punti della piattaforma non è cambiato niente… hanno solo visto che sollevandosi leggermente ha cambiato il verso di rotazione su stessa. Comunque sembrerebbe proprio una di loro.
Tutto è pronto per l’esperimento. La pallina P, appartenente al sistema inerziale, deve percorrere la sua traiettoria verticale con velocità costante, partendo dal centro e dirigendosi verso il bordo in alto L’abbiamo rappresentata con un faccino sorridente, dato che ciò che deve fare è oltremodo semplice e, inoltre, le è stato detto di stare zitta.
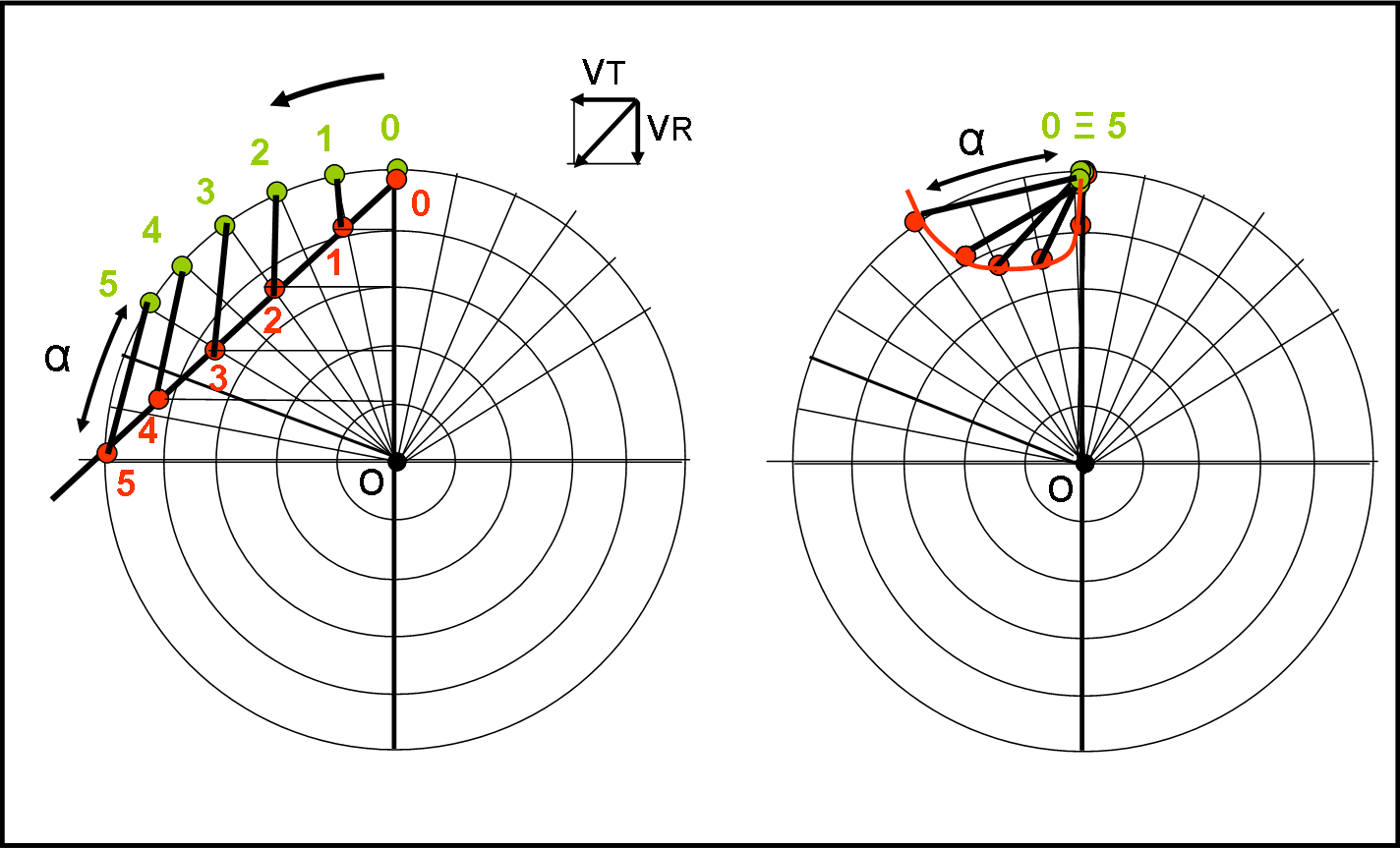
La parola va invece a tre punti rossi del sistema in rotazione. Loro sono perfettamente solidali tra loro e quindi si muovono con velocità angolare costante. Come già detto, però, ciò non toglie che quelli più esterni siano obbligati a percorrere uno spazio più lungo per potere stare in fila con gli amici. Se non fosse così la piattaforma si sgretolerebbe… In Fig. 12 vediamo la configurazione iniziale.
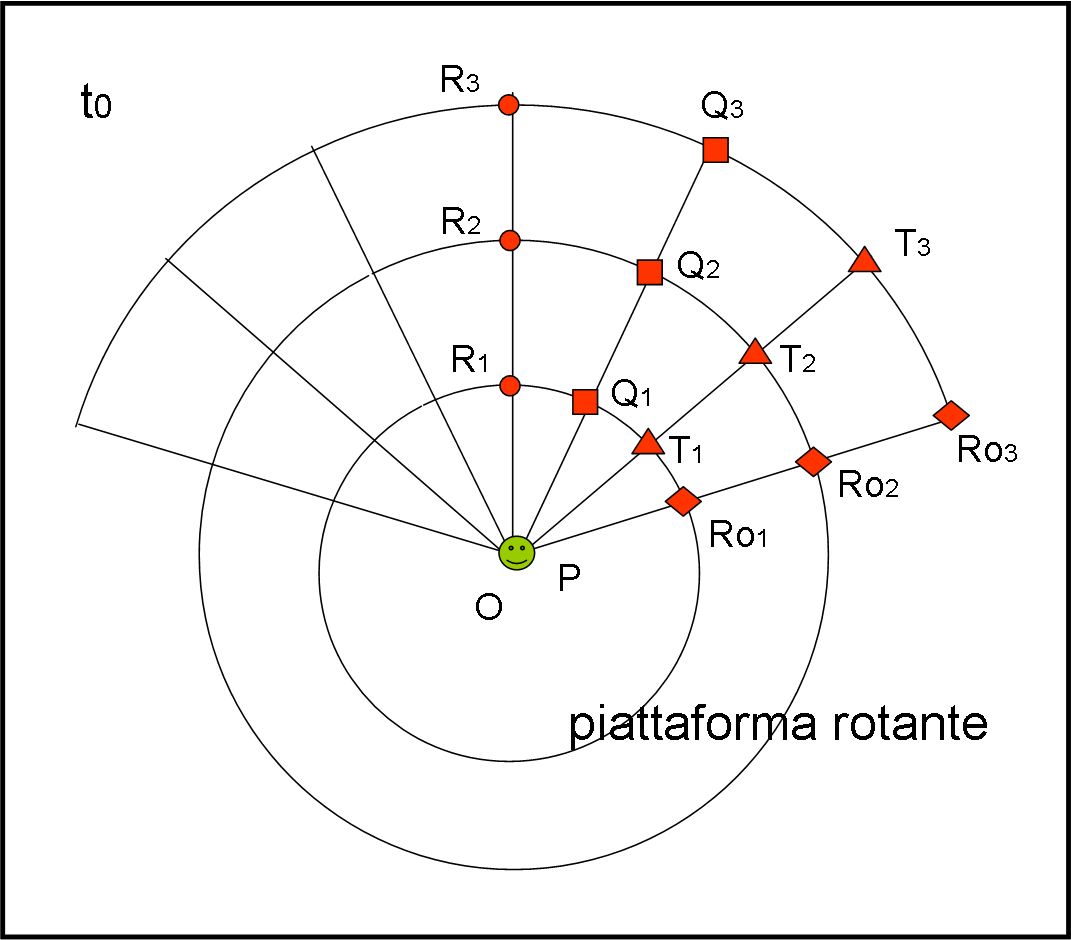
Al tempo t0, la pallina P e i tre amici rossi (del sistema rotante), R1, R2 e R3, sono perfettamente allineati. Dietro di loro, su altre tre linee solidali, vi sono gli amici quadrati (Q1,Q2 e Q3) che, come quelli successivi (T1,T2 e T3 e Ro1,Ro2 e Ro3) serviranno per ottenere conferma delle varie posizioni raggiunte da P. I punti della piattaforma hanno studiato una bella strategia per non sbagliare nemmeno una virgola! Cinematica e Dinamica, in fondo, se ne compiacciono.
Viene dato il via a P, mentre si inizia a far ruotare la piattaforma (senza, ovviamente, dirlo ai punti rossi e ai loro amici: devono rimanere convinti di rimanere FERMI). Nel tempo Δt (sarebbe molto meglio se fosse un … dt) che la pallina impiega per arrivare al prima circonferenza, i punti rossi hanno raggiunto la seconda linea radiale verso sinistra. Siamo nelle condizioni della Fig. 13, al tempo t1 = t0 + Δt .
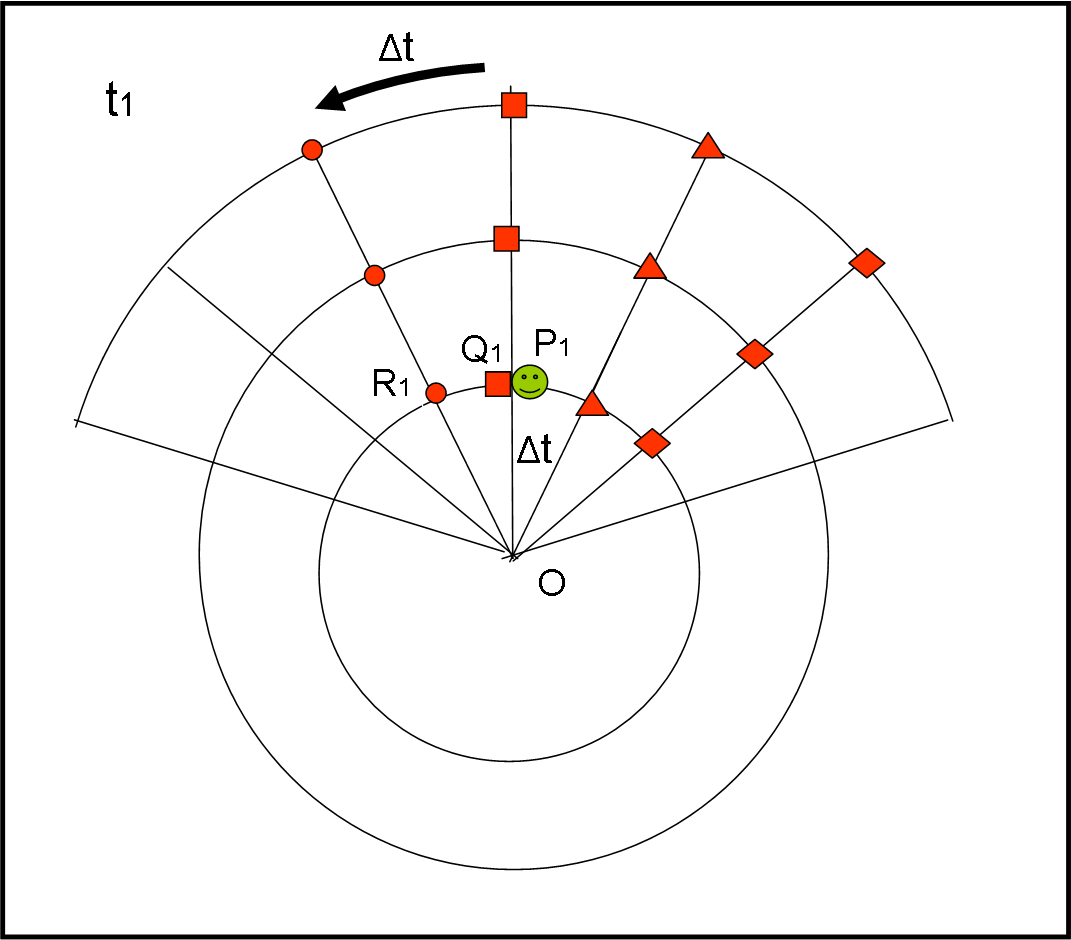
La parola va a R1: “Ho visto chiaramente la pallina P venire verso di me in senso radiale, ma continuava anche a spostarsi verso destra di un arco di circonferenza che mi pare sia perfettamente uguale a quello che c’è tra me e l’amico quadrato.” L’amico quadrato Q1 urla subito: “Sì, sì, hai proprio ragione. Infatti in questo istante è proprio qui dove sono io. Ma vedo che continua salire e credo anche a spostarsi verso destra”.
Passa un altro intervallo Δt e arriviamo al tempo t2 (Fig. 14).
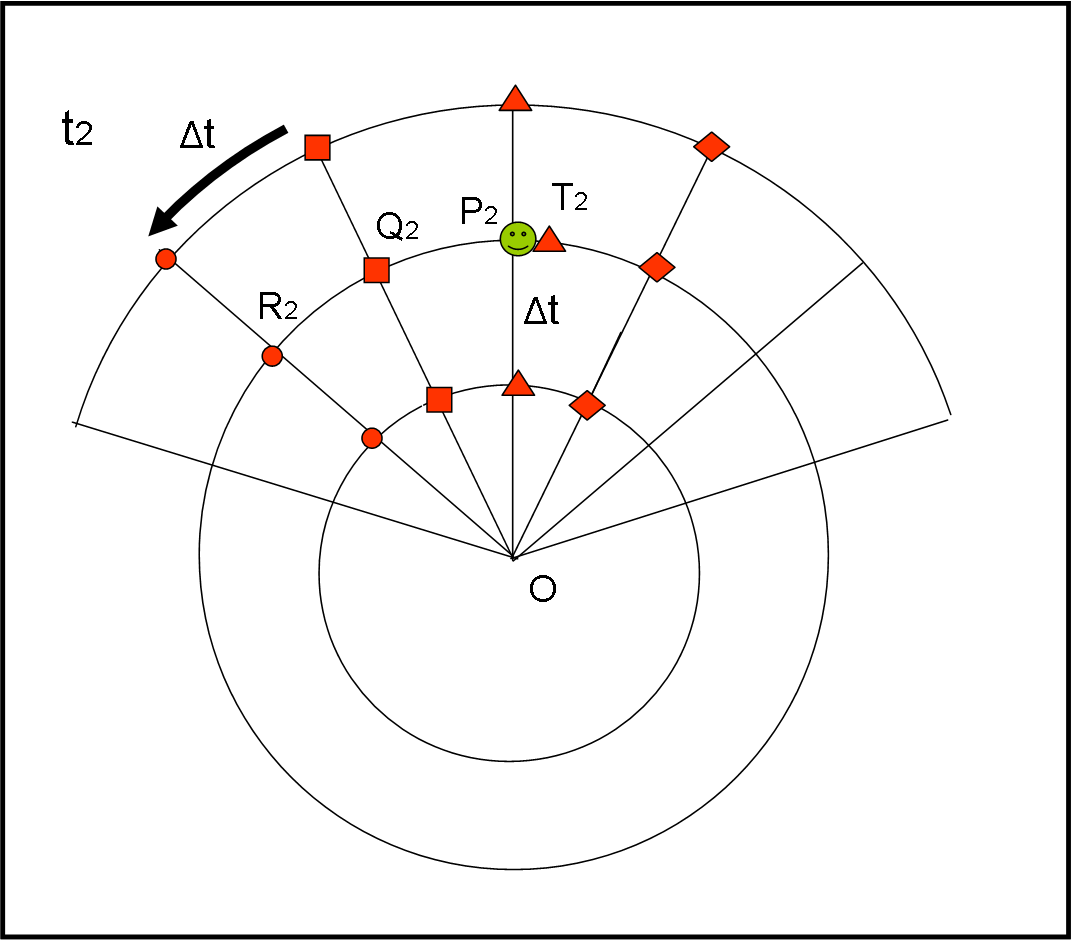
Il punto rosso R2 prende la parola: “Ha proprio ragione Q1… continua a salire, ma anche a spostarsi sempre di più verso destra… A me sembra che abbia percorso un tratto pari a quello che esiste tra me e Q2. Q2 conferma, ma chiede a T2. Anche lui non ha dubbi: “Sì, avete ragione è proprio arrivata qui da me. Confermo lo spostamento verso l’alto e un aumento dello spostamento verso destra pari a quanto dista Q2 da me”.
Il movimento di P continua (e la pallina continua a sorridere per come il suo movimento, così semplice, venga raccontato dai poveri punti della piattaforma), come mostrato in Fig. 15.
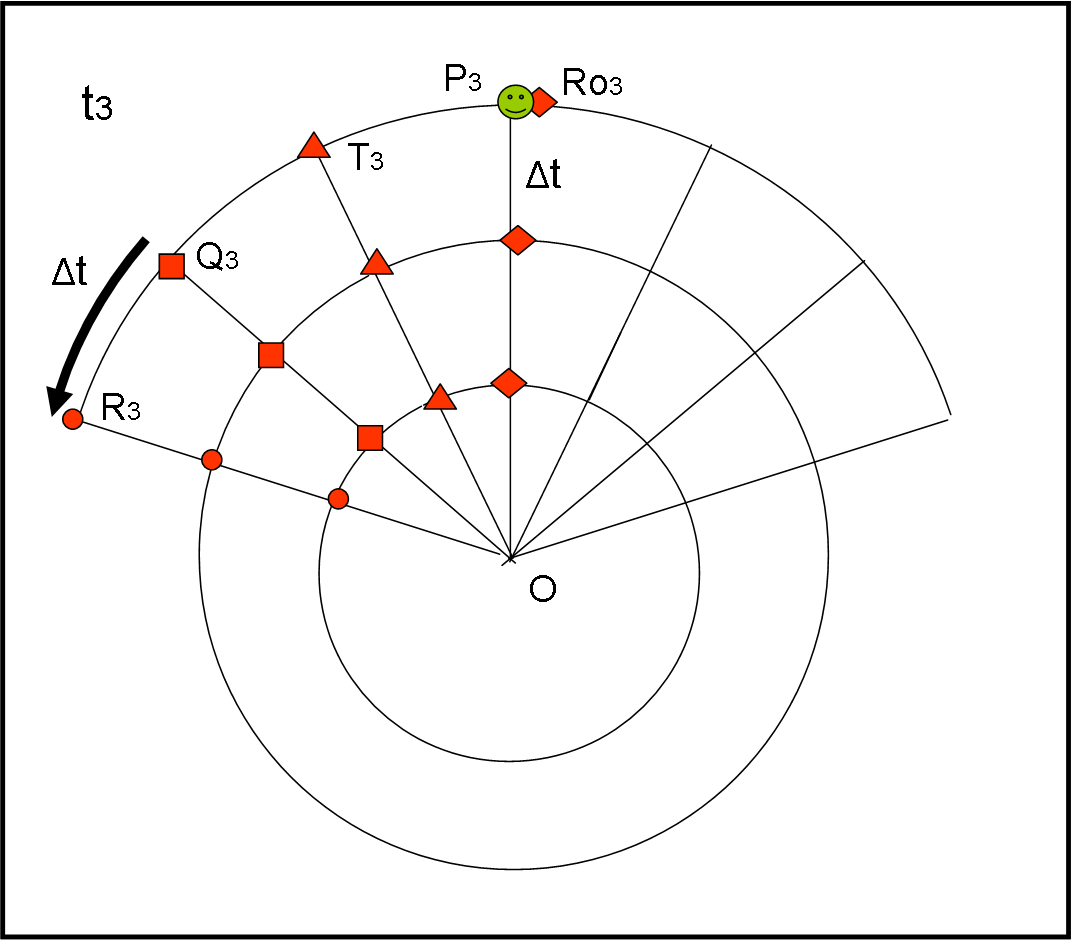
Al tempo t3 si è portata in P3, un movimento normalissimo. La parola va adesso a R3: “Faccio fatica a vedere la pallina, tanto si è allontanata da me. Non vorrei sbagliare ma mi sembra che si sia spostata di ben tre volte la distanza tra me e Q3. Q3 conferma che l’ha visto allontanarsi verso destra, ma è meglio chiedere a T3. “Sì, sì, l’ho vista proprio dirigersi verso Ro3… chiediamo a lui”. “Confermo in pieno”, risponde Ro3, “quanto detto dai miei amici e colleghi. P è proprio qui accanto a me!”.
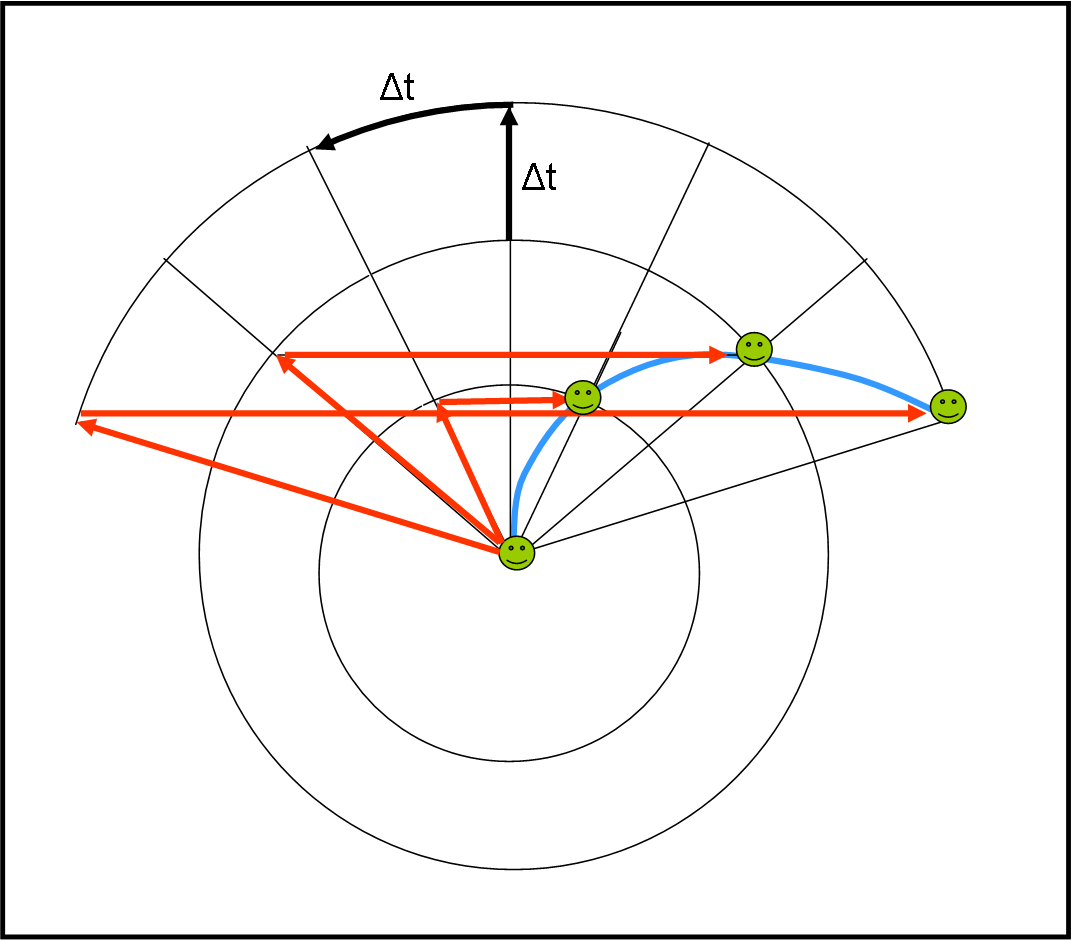
L’esperimento si può considerare concluso e Cinematica e Dinamica vanno a segnare le posizioni di P al variare del tempo, secondo quanto detto dai punti della piattaforma. Tenendo presente che loro si sono considerati fermi, devono segnare i punti nella configurazione di partenza, ossia nella Fig. 12. Ciò che si ottiene è la Fig. 16, dove le posizioni assunte da P, secondo il sistema rotante, sono segnate in nero.
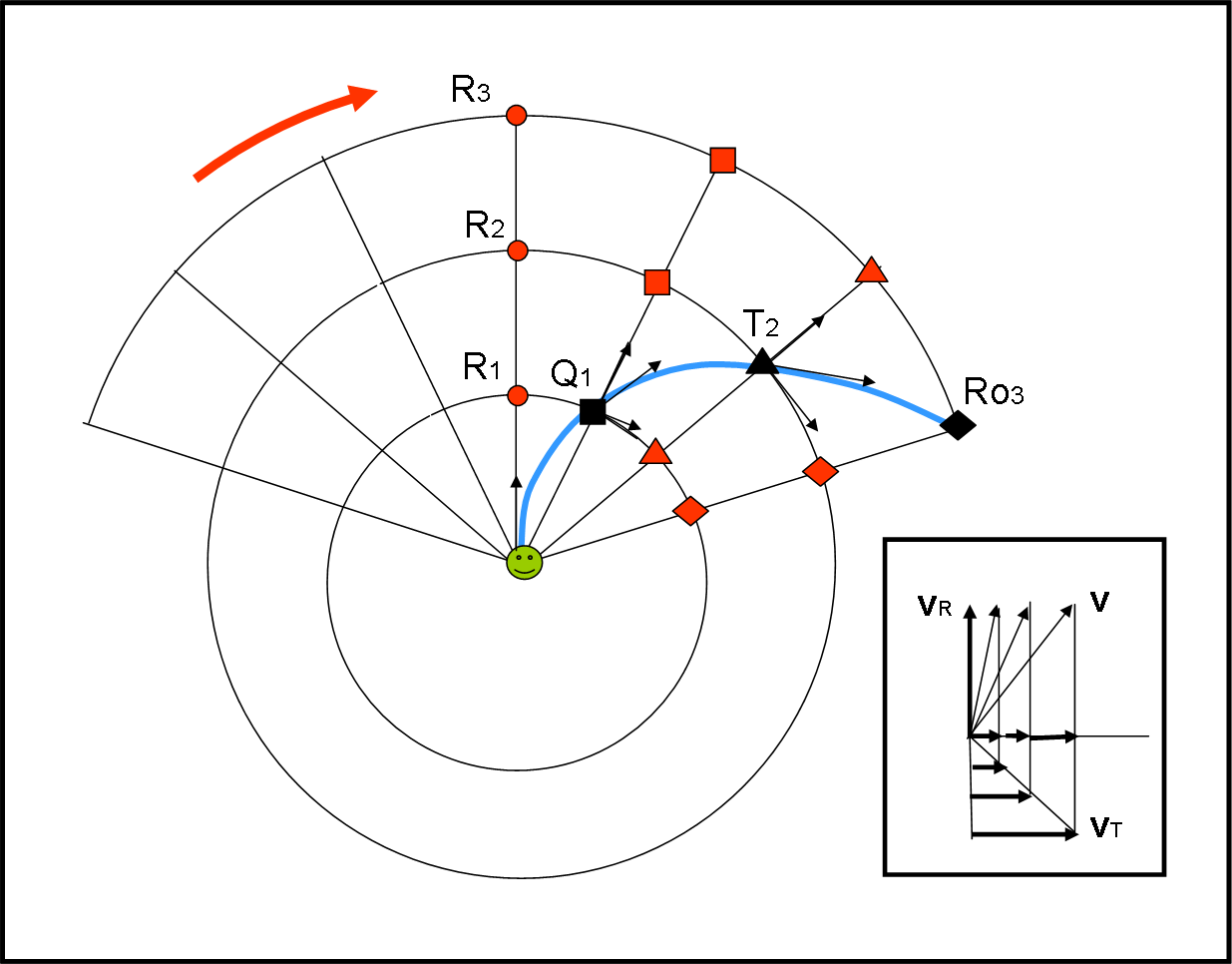
Facciamo una piccola analisi delle velocità in gioco secondo il sistema rotante. Ogni punto P ha una velocità radiale e una tangenziale (relativa alle circonferenze in cui si trovano i vari punti P secondo il sistema rotante). Mentre il modulo della velocità radiale è sempre lo stesso, cambia invece il modulo della velocità tangenziale (ci spostiamo verso l’esterno). Le velocità sono state tracciate in Fig. 16 e nel riquadro in basso a destra.
Ne nasce una strana curva che è causata da almeno due accelerazioni, che devono dare un senso fisico alla soluzione. Per arrivare ad esse bisogna notare che la velocità radiale ha modulo costante ma varia la direzione, mentre quella tangenziale varia anche in modulo. Insomma, deve comparire sia un’accelerazione centrifuga, dato che vi è un allontanamento in senso radiale, ma anche quella di Coriolis che dipende dalla velocità lungo la traiettoria. Tutto ciò può essere ottenuto partendo dalle formule ricavate all'inizio, manovrando sapientemente la… mano destra.
In poche parole: secondo il sistema rotante la pallina che si muove verticalmente, appare sempre “IN RITARDO” rispetto ai punti della piattaforma e, dato che loro si considerano fermi, appare spostarsi sempre di più verso l’esterno e verso destra.
Tutto questo da un punto di vista “fisico”…
Da un punto di vista geometrico e pratico (non arrabbiatevi!), risulta subito chiaro, dalla Fig. 17, un metodo più immediato per costruire velocemente e semplicemente la curva descritta da P.
Basta tracciare i raggi, per intervalli di angolo costanti, e, quindi, anche di tempo costante (la velocità angolare è costante). Intervalli di tempo che vengono descritti anche dalla pallina per passare da una circonferenza più interna a una più esterna. Poi basta seguire le frecce rosse… banale e concettualmente più che intuitivo! Detto tra noi, non abbiamo fatto altro che usare delle coordinate polari, ben più comode, in questo contesto, rispetto a quelle cartesiane … ma sapete, sono sempre un po’ malvagio… e, poi, in fondo, quelle belle figure con i triangoli rotanti erano tanto simpatiche…
Tra parentesi, lavorando con i triangoli (cartesiani), si poteva arrivare alla soluzione più comoda e rapida , trafficando un poco con la geometria. Ce lo mostra la Fig. 18, dove il blu si riferisce al “vecchio” metodo e il rosso a quello “nuovo”. Non vi è bisogno di ulteriori parole…
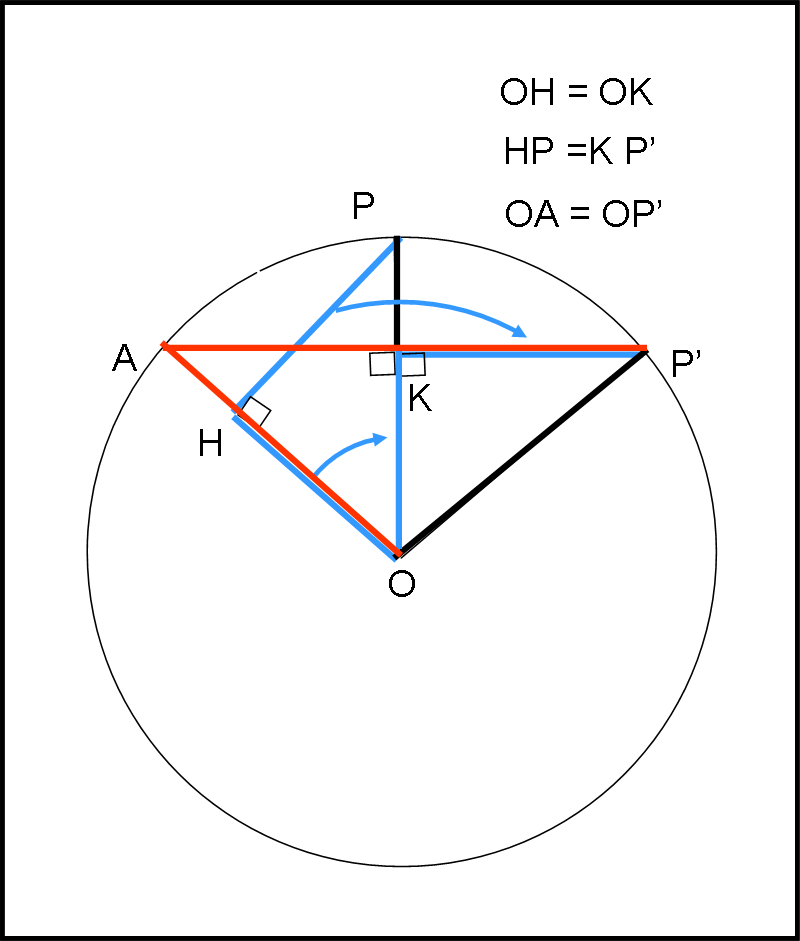
Probabilmente, molti di voi avranno fin da subito adottato il secondo metodo, ma io ho preferito eseguire i due passaggi per arrivare lentamente all’essenza fisica, partendo da una puramente geometrica. I più preparati non si offendano... prima o poi passeremo nuovamente a usare qualche formula.
L'importanza delle condizioni di partenza
E’ giunta l’ora di tirare un po’ le somme. Vediamo, perciò, se abbiamo capito bene ciò che succede con questi sistemi inerziali e non inerziali. In particolare, cominciamo a definire per bene cosa si vede o non si vede passando da un sistema all’altro. Avete già capito che la forza di Coriolis domina la situazione (ma non solo…). Sfruttiamo, allora, le caratteristiche del nostro pianeta amico Papalla, dove non c’è atmosfera e gli abitanti amano moltissimo le gare.
Su Papalla vi sono due grandi aeroporti, uno posto esattamente al Polo Nord e uno posto sull’Equatore. Alla gara partecipano due aerei di linea e due astronavi. Gli aerei sono parcheggiati nell’aeroporto, mentre le astronavi sono tenute in stallo sopra gli aeroporti, manovrando alcuni motori aggiuntivi (ma a noi poco importa). I due aerei sono AE e AP, mentre le due astronavi sono ASE e ASP . Lo scopo della gara è quello di raggiungere l’aeroporto opposto, ossia AP e ASP devono raggiungere l’aeroporto all’equatore e viceversa per AE e ASE.
Ricordiamo che Papalla ruota intorno al suo asse come fa la Terra (l’asse passa per il Polo Nord e il senso di rotazione è quello antiorario se visto da PN) e, come sappiamo bene, non ha atmosfera. Trascuriamo del tutto anche gli effetti della gravità.
Le condizioni della gara sono quelle della Fig. 19 che segue.
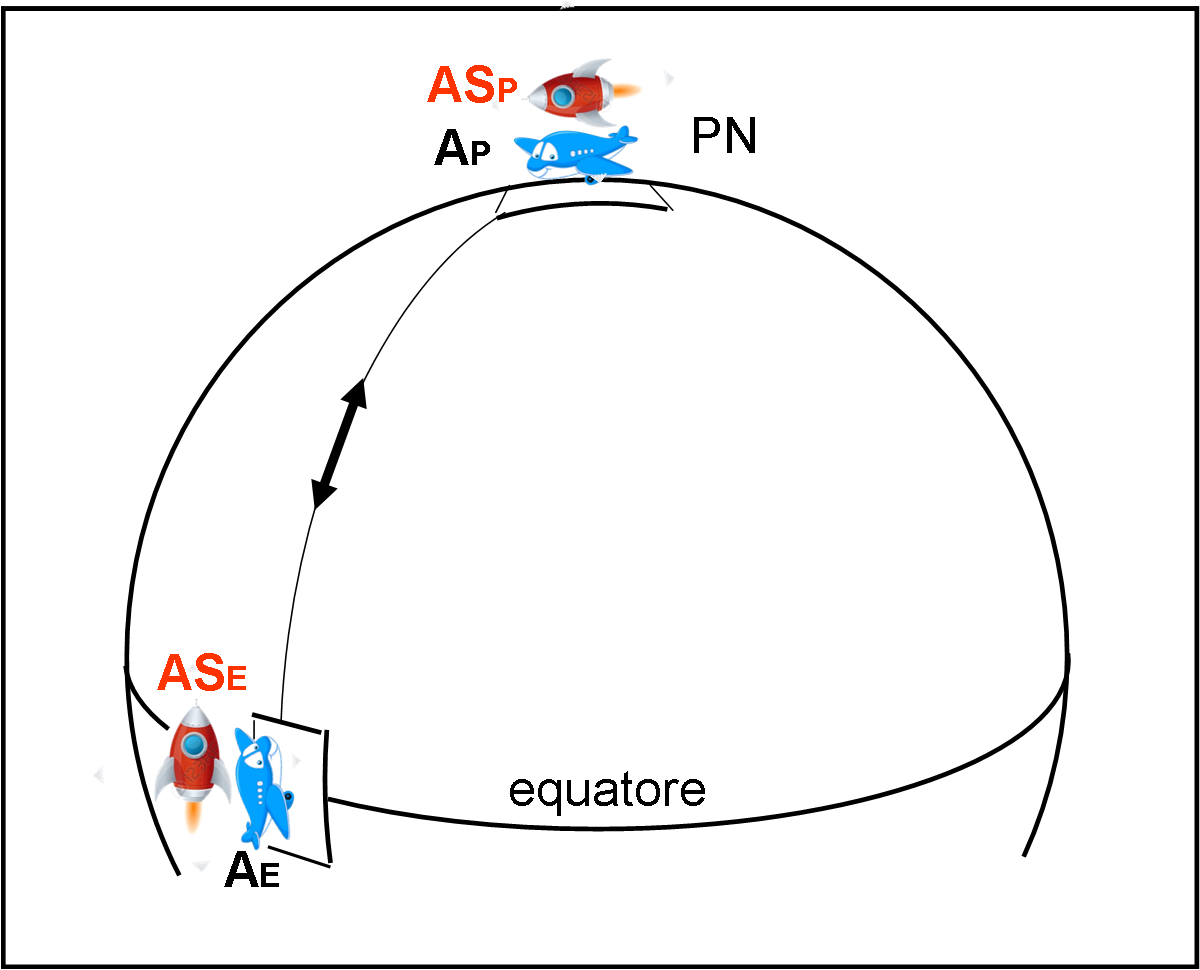
I piloti ci pensano un po' sopra e poi decidono tutti di seguire la rotta apparentemente più corta, ossia quella del meridiano che passa per i due aeroporti nell'istante della partenza. Una volta stabilita la rotta non la si può più cambiare! Le astronavi fermano i motori che le tenevano in sospensione e si lanciano verso i rispettivi traguardi. I due aerei fanno lo stesso, dopo essere decollati dagli aeroporti.
Per non cadere in confusione, possiamo dire che le astronavi sono del tutto estranee al pianeta (un po’ come quella che aveva spaventato l’Italia ).
Le domande a cui vogliamo rispondere sono le seguenti:
1) Quali tra i quattro velivoli raggiungeranno il traguardo?
2) Tracciare le traiettorie dei quattro velivoli, sia in un sistema di riferimento che nell’altro.
aver inserito Papalla (ma anche la Terra...) nel nostro problema complica decisamente la faccenda. Infatti, abbiamo parlato sempre di moto a velocità costante di un oggetto su una superficie rotante. La Terra vista dal polo assomiglia molto a un disco rotante, tuttavia non lo è esattamente, in quanto se l’aereo si muove con velocità costante, s’intende che la sua velocità è misurata rispetto al suolo che è curvo. Ne consegue che la sua velocità sull’ipotetico disco rotante (la Terra proiettata sul piano equatoriale) deve essere variabile, come illustra la Fig. 20.
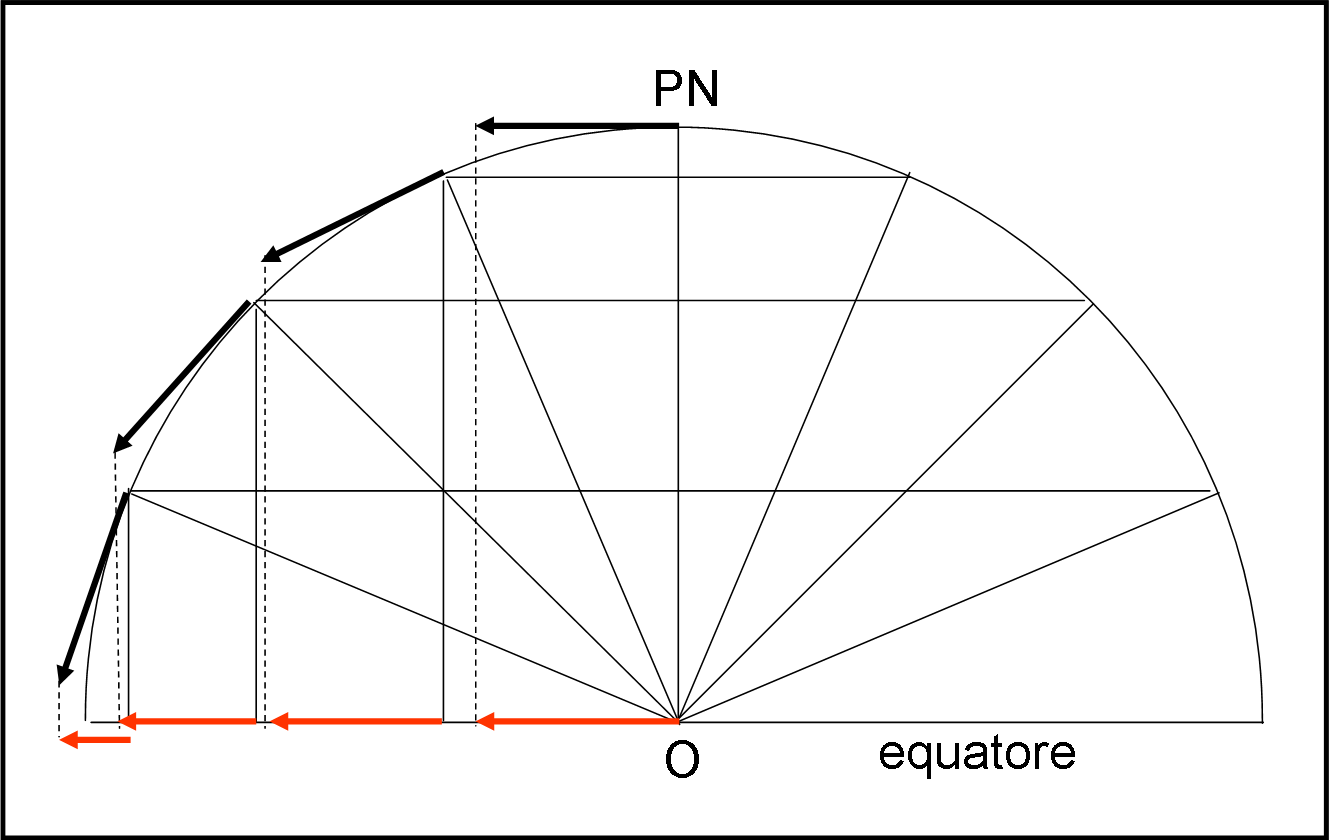
Lo stesso tratto di circonferenza comporta lunghezze, nella proiezione, crescenti avvicinandosi ai poli e viceversa. Inoltre non consideriamo la forza di gravità che dà un suo aiuto nel muoversi variando la latitudine. Insomma, è molto meglio semplificare ancora di più il quiz (basta e avanza) e ridursi a un disco rotante, in cui la velocità rimanga veramente costante. Già cosi ne vedremo delle belle…
Riproponiamo, allora, la gara traslocando il tutto su una piattaforma girevole piana (i risultati saranno praticamente gli stessi).
Cominciamo con la Fig. 21.
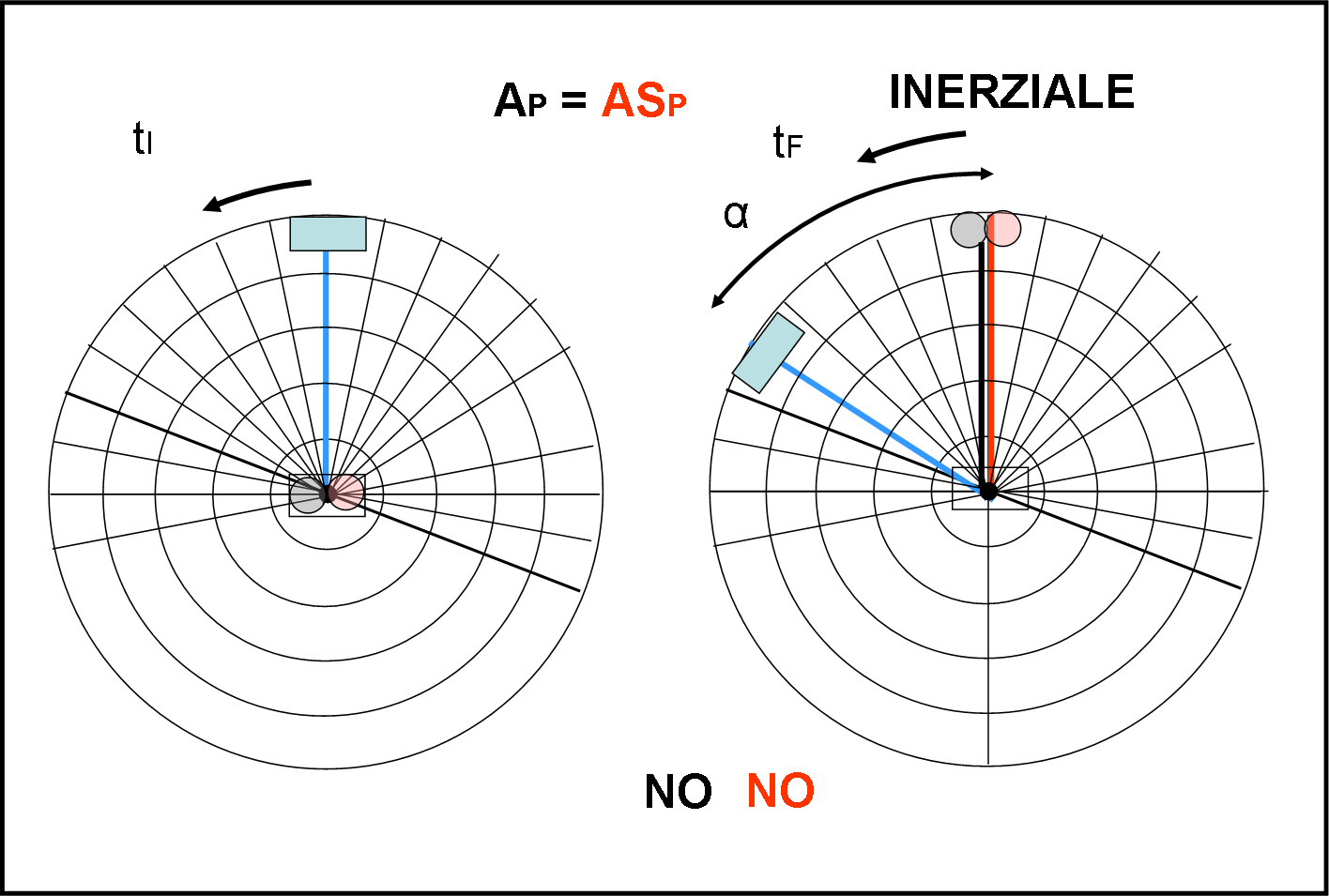
In questo caso abbiamo l’aereo e l’astronave che sono nel punto centrale e devono mirare all’aeroporto posto ai bordi della piattaforma (rettangolo celeste). Vediamo il tutto nel Sistema Inerziale. Non ci vuole molto a capire che partendo dall’origine poco importa che l’aereo appartenga al sistema inerziale e l’astronave no. L’origine è la stessa per entrambi i sistemi e quindi l’aereo e l’astronave non subiscono nessuna velocità prima della partenza: nessuno dei due ruota (ovviamente consideriamo aerei e astronavi puntiformi). Al tempo tI essi vedono l’aeroporto davanti a loro e partono immediatamente, mantenendo una traiettoria rettilinea. Riescono a farlo benissimo, essendo svincolati dalla rotazione e non avendo velocità “residue”, solo quella di volo.
Tuttavia, quando arrivano sull’equatore (bordo esterno della piattaforma), al tempo tF, l’aeroporto non è certo stato fermo! Esso ha ruotato di un certo angolo α ed è decisamente più avanti dei due velivoli. Nessuno dei due raggiunge l’aeroporto, ma un punto spostato verso destra rispetto a lui.
In Fig. 22 riproponiamo l’esperimento, mettendoci, però, nel sistema rotante.
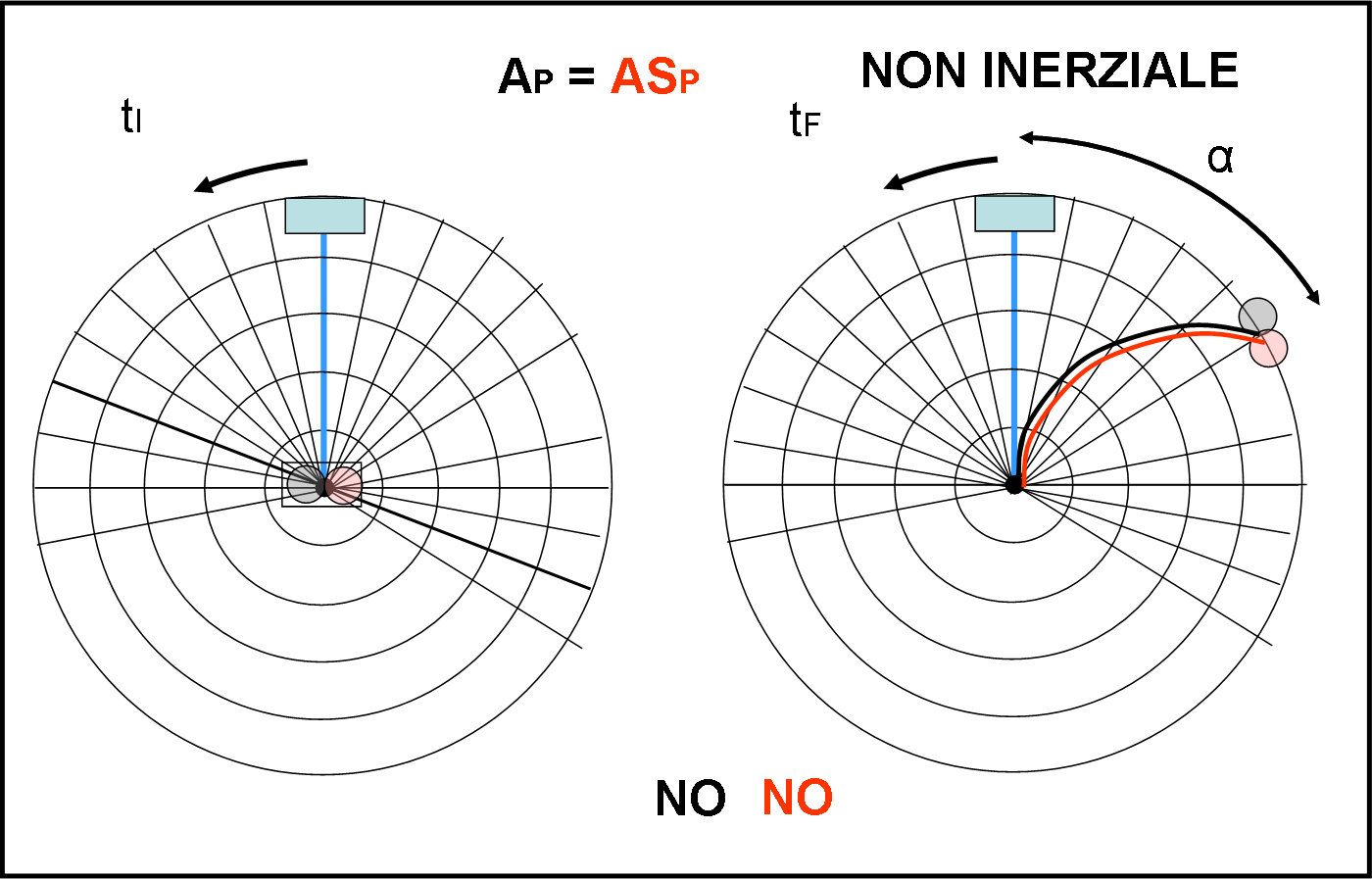
Potremmo già concludere che niente può cambiare nell’esito finale: il fenomeno meccanico deve restare lo stesso… cambia solo il modo di spiegarlo e per far ciò si devono introdurre forze fittizie. Tuttavia, è sempre interessante studiare e descrivere la traiettoria che seguono aereo e astronave per “mancare” di molto l’aeroporto di arrivo. Beh… per costruire la traiettoria basta seguire uno dei metodi descritti e si ottengono due curve identiche, dato che le condizioni sono le stesse. Ovviamente la curva ci dice che sono in azione sia la forza centrifuga (in senso radiale) che quella di Coriolis (perpendicolare alla traiettoria), in modo tale da far atterrare sia l’astronave che l’aereo nello stesso punto, alla stessa distanza dall’aeroporto che dovevano raggiungere. Questa distanza angolare è, ovviamente, α.
Passiamo adesso al caso in cui i velivoli partano dall’aeroporto equatoriale.
Mettiamoci nel sistema inerziale (Fig. 23).
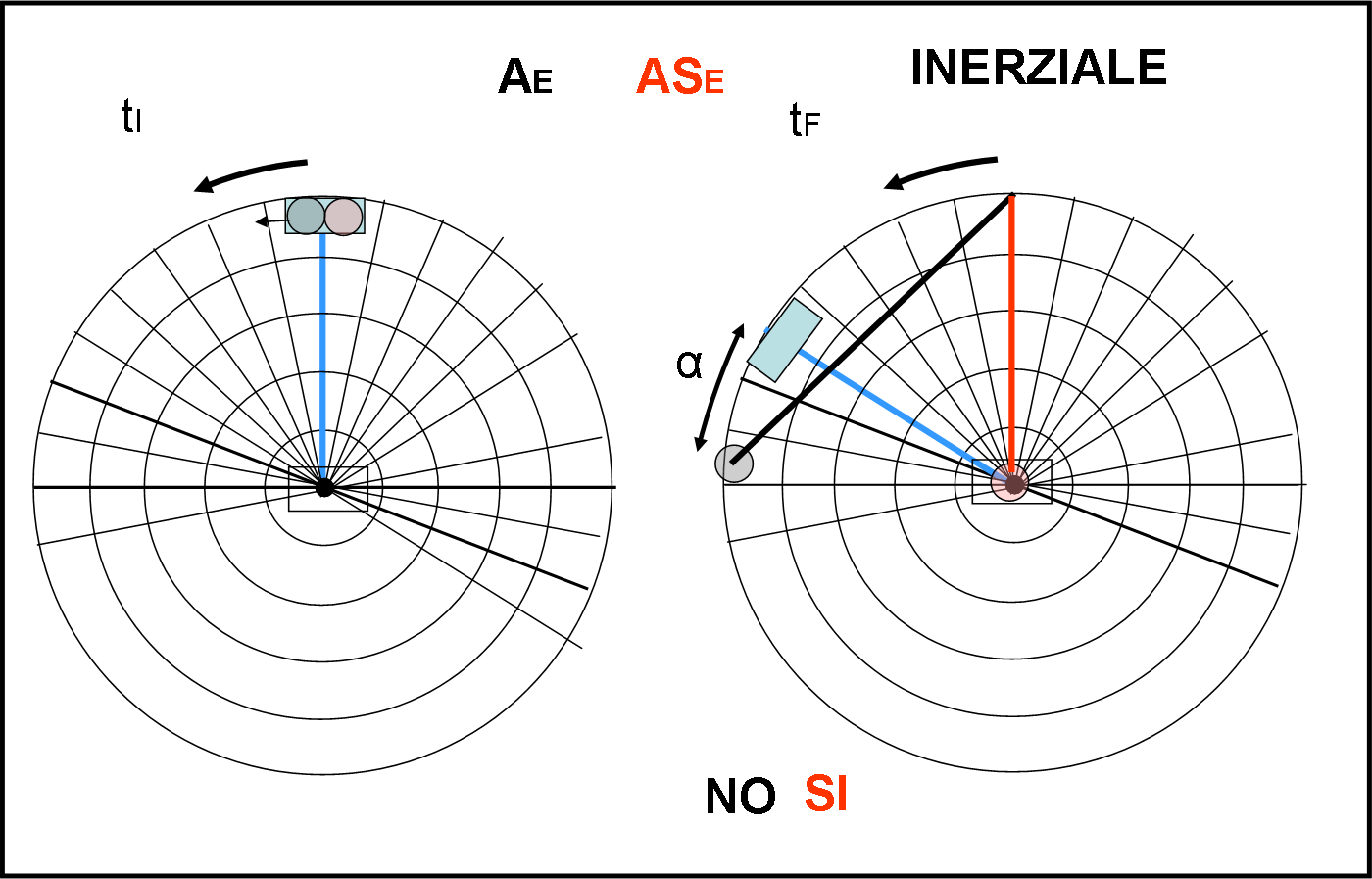
Le due traiettorie differiscono immediatamente. L’astronave vive nel sistema inerziale e quindi è FERMA nel suo sistema. L’unica velocità a cui è soggetta è quella che la fa dirigere verso l’aeroporto polare. Il centro, ossia il polo, non subisce rotazione, per cui essa non ha nessuna difficoltà a raggiungere l’aeroporto: operazione riuscita! L’aereo , invece, sta girando insieme alla piattaforma e quindi ha una sua velocità intrinseca tangenziale (moto circolare uniforme). Anche se lo poniamo al di fuori della piattaforma durante il volo, questa componente non viene cancellata (principio d’inerzia).
A questa si deve sommare la velocità diretta verso il centro. La sua traiettoria è, di conseguenza, la retta nera diretta verso destra rispetto alla rotazione. Non solo l’aereo non raggiunge il polo, ma, a momenti, torna da dove è partito! Riesce, infatti, ad anticipare, solo dell’angolo α, l’aeroporto equatoriale che sembra quasi inseguirlo… In poche parole, l’astronave riesce a raggiungere il bersaglio, mentre l’aereo sembra proprio impazzito.
Non ce ne sarebbe nemmeno bisogno, ma concludiamo guardando cosa si vede nel sistema non inerziale in Fig. 24.
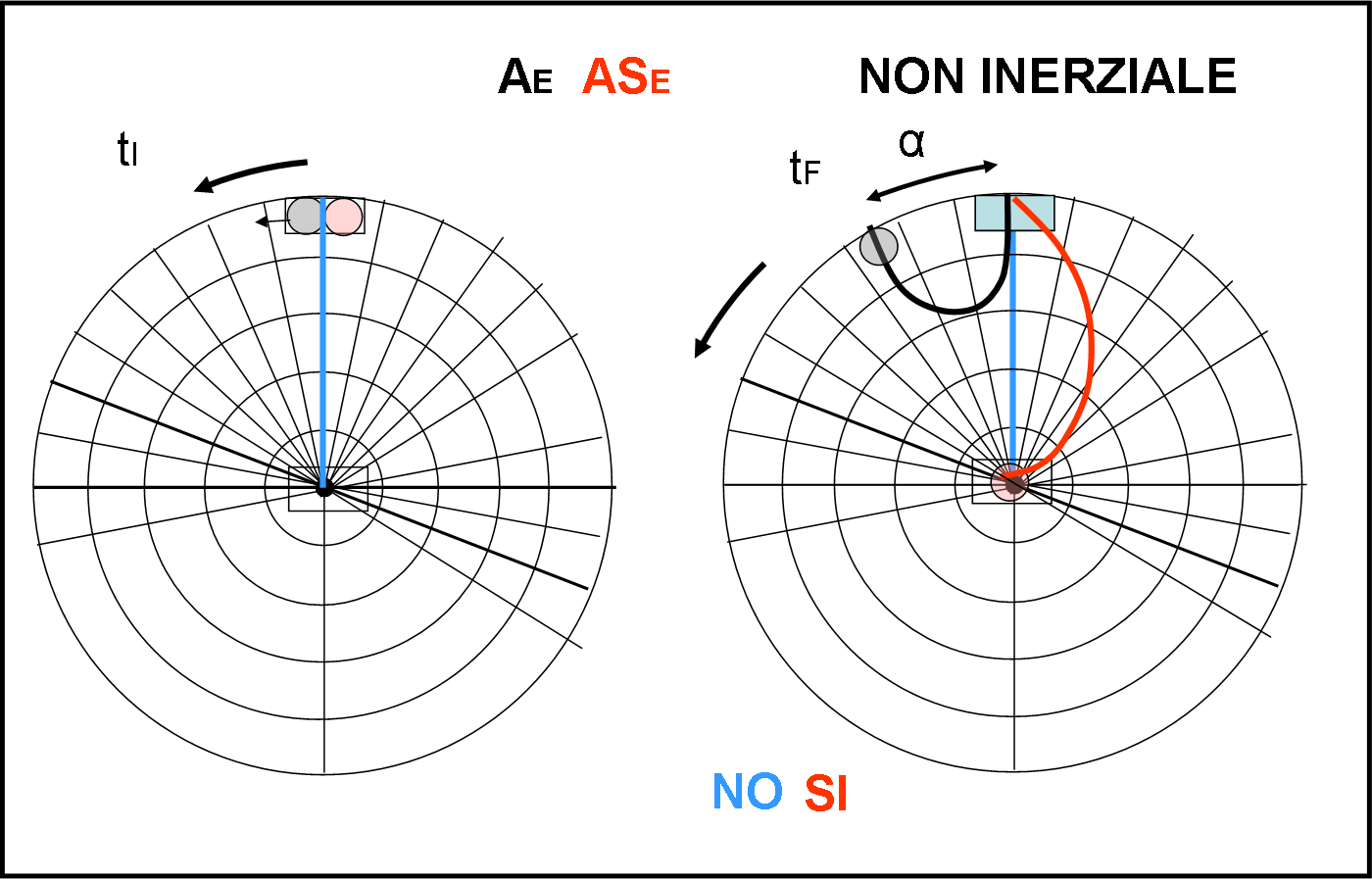
Qui devono apparire delle curve, dato che devono agire le forze fittizie. Cosa succede all’astronave? Facile a ricavarsi. Lei sembra andare verso sinistra, fa un bel giro, ma poi non può che arrivare alla meta (ricordiamo l'apparente attacco alieno dell'astronave all'Italia...). Ricordiamoci sempre che questo è ciò che vede chi si muove come l’aeroporto di partenza.
Passiamo all’aereo apparentemente impazzito… Tutto viene confermato: lui tende ad andare verso il centro, ma poi viene sbattuto verso l’esterno fino a uscire dalla piattaforma. Ovviamente, l’angolo tra aeroporto equatoriale e uscita dell’aereo deve essere sempre uguale ad α.
Concludendo: l’unica a raggiungere l’aeroporto finale è l’astronave che parte dall’equatore. Non ho voluto ripetere ancora una volta tutta la costruzione della traiettoria. Inserisco, però, un altro “metodo” anch’esso abbastanza intuitivo. Utilizziamolo per il viaggio dell’aereo equatoriale, il più bizzarro dei quattro. Andiamo nella Fig. 25.
La divisione della figura di sinistra in tanti settori circolari uguali e in tanti cerchi concentrici ci dice solo che nel tempo che la pallina verde solidale con la piattaforma si porta sul raggio successivo, la pallina rossa si porterebbe su un cerchio più piccolo. Tuttavia, la pallina rossa subisce anche la velocità costante tangenziale e quindi si muove lungo la linea inclinata e le posizioni successive si trovano mandando le parallele orizzontali che partono dalle posizioni successive lungo la verticale (o combinando le due velocità coinvolte).
In poche parole, la pallina si muove nell’unità di tempo di un tratto che corrisponde a una velocità tangenziale (spazio percorso in senso orizzontale) sommata a una velocità radiale (spazio percorso in senso verticale), come mostrato nel piccolo diagramma di destra (somma vettoriale). Ne segue, ovviamente, che nello stesso tempo in cui la pallina verde percorre l’arco di cerchio, la pallina rossa si sposta di una certa quantità costante lungo la linea inclinata.
In conclusione, nei vari tempi considerati, pallina verde e pallina rossa devono trovarsi nelle rispettive posizioni: 1 con 1, 2 con 2, e via dicendo. Uniamo queste posizioni con un segmento rigido. Consideriamo adesso il “sistema” pallina verde, pallina rossa (e segmento che le unisce) e raggio relativo alla pallina verde ( O-1, O-2, ecc.).
Per vedere cosa succede nel sistema non inerziale (che si considera fermo), rappresentato nella parte destra della figura, bisogna riportare i vari raggi O-1, O-2, e tutto ciò che è “bloccato” a lui (come detto prima)… su quello di partenza (O-0), dato che tutti i pallini verdi devono coincidere, così come i raggi corrispondenti. La pallina rossa assumerà le posizioni successive viste nel sistema rotante. Ovviamente, l’angolo α deve essere lo stesso.
E tre! Un nuovo metodo per tracciare la traiettoria influenzata pesantemente dalla forza di Coriolis e da quella centrifuga. No, non fatevi prendere in giro... essi sono tutti la stessa cosa, anche se spiegati in modo apparentemente diverso. Siamo di fronte, solo e soltanto, a un cambiamento di coordinate!
Ribadisco ancora che stiamo lavorando sempre con velocità rettilinee uniformi. Nulla ci vieterebbe di costruire le traiettorie anche con velocità sempre rettilinee, ma non costanti. Tuttavia, cambierebbe un po’ la forma della curva, ma il concetto di base no. Per cui possiamo anche permetterci di non complicare ulteriormente la faccenda. Questo varrà sia per i moti terrestri che per il moto del pendolo. Capire le forze agenti e la traiettoria finale nel sistema non inerziale è già un esercizio abbastanza intrigante e divertente.
Generalizziamo le traiettorie dell'aereo equatoriale
Il punto chiave è vedere graficamente come agiscono le forze centrifuga e di Coriolis sul moto rettilineo e uniforme di un oggetto (aereo) che vari la sua velocità in rapporto a quella di rotazione della piattaforma da cui parte. Ne vedremo delle belle, soprattutto per velocità lineari molto ridotte...
Il rapporto su cui vogliamo lavorare è vR/vT, dove vR è la velocità costante intrinseca (in modulo, direzione e verso) dell'aereo, sollevato dalla sua posizione nella piattaforma rotante (ossia inserito nel sistema inerziale). L'importante è partire con il caso limite, ossia quello in cui la velocità dell'aereo sia ZERO, ossia l'areo sia soltanto spostato in alto in modo da non appartenere più al sistema rotante. Ovviamente non sta fermo, ma si muove seguendo la velocità tangenziale che aveva quando era ancorato al suolo, sulla piattaforma rotante. Siamo perfettamente nel caso della famosa pallina che ruota, tenuta da una corda, quando la si tagli.
Ovviamente, vogliamo vedere come la traiettoria dell'aereo appare a un osservatore che continui a stare nell'aeroporto... Un po' alla volta, aumentando il rapporto vR/vT , l'aereo sembrerà proprio impazzito soprattutto per valori di vR molto bassi. Poi le cose diventeranno più "normali". Ovviamente si può arrivare al caso in cui il rapporto tende a infinito....
Come già detto precedentemente, possiamo usare il metodo che preferiamo (sempre di cambiamento di coordinate si tratta).
La figura da cui partire è quella che segue (Fig. 26). La base di tutto è che nel tempo in cui la piattaforma ruota di un angolo θ, l'aereo P si muove, nel sistema inerziale, di un segmento s, sempre andando nella direzione AO. Il movimento verso O è, però, solo quello dovuto al moto intrinseco dell'aereo. Il punto A è l'aeroporto solidale con la piattaforma.
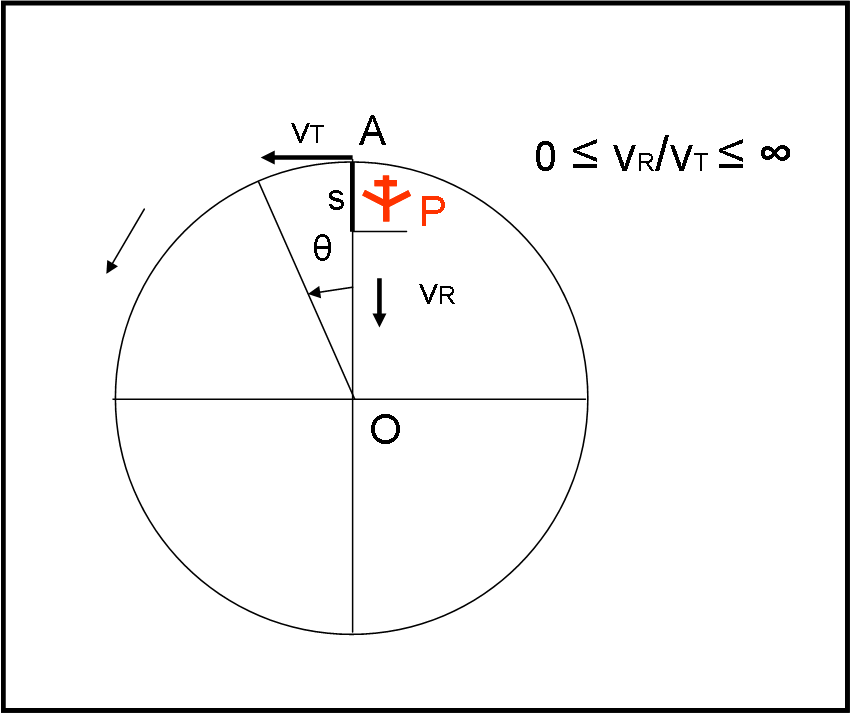
Il succo di tutto è che un aereo che vola senza attrito su una piattaforma rotante, partendo dal bordo esterno (aeroporto equatoriale), è vincolato ad essa, prima di lasciarsi andare a un tragitto libero e inerziale. Ne segue che DEVE conservare la velocità tangenziale che possedeva mentre stava ruotando parcheggiato in aeroporto. Questa situazione deriva direttamente dal principio d’inerzia: se eliminiamo la forza centripeta che obbliga ogni punto della piattaforma a ruotare, aereo compreso, esso se ne va direttamente per la tangente, come ormai sappiamo molto bene.
La parte interessante di questa costruzione dipende, perciò, solo e soltanto, da come si combina la velocità tangenziale “residua” con quella del volo vero e proprio (vT e vR). Ovviamente la velocità risultante sarà sempre costante, ma inclinata rispetto a quella puramente verticale della direzione impostata dal pilota. La costruzione si ottiene con la solita somma vettoriale. In parole povere, partiamo da una traiettoria orizzontale (vR = 0, l’aereo si stacca dall’aeroporto, ma non accende i motori), fino al caso in cui vT = 0, ossia la velocità dell’aereo è talmente alta che la piattaforma può essere considerata immobile, ossia diventa un sistema inerziale.
Se guardassimo le varie situazioni da un sistema inerziale, vedremmo la piattaforma (e l’aeroporto) ruotare, mentre l’aereo seguirebbe delle rotte rettilinee che partono da una orizzontale e finiscono a una verticale, come mostra la Fig. 27, dove ne abbiamo disegnata qualcuna a caso.
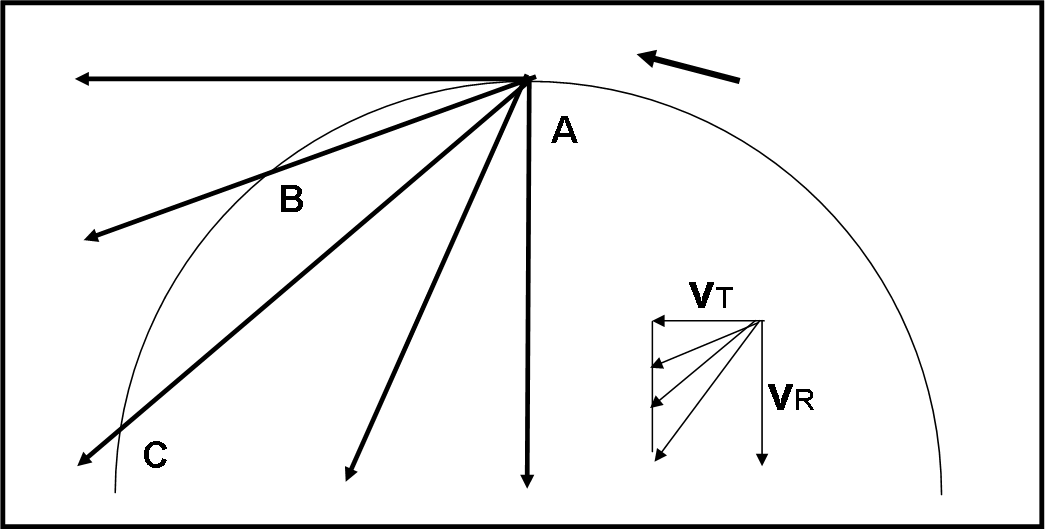
Per ottenere ciò, possiamo mantenere costante la rotazione (ossia vT) e aumentare sempre più vR. L’importante è notare che in due casi l’aereo abbandona la piattaforma in B e C. Ebbene questo è il fenomeno meccanico che dobbiamo mantenere, cambiando sistema di riferimento. L’arco AC o AB dovrà restare lo stesso anche se guardiamo lo strano volo dell’aereo restando fermi in aeroporto.
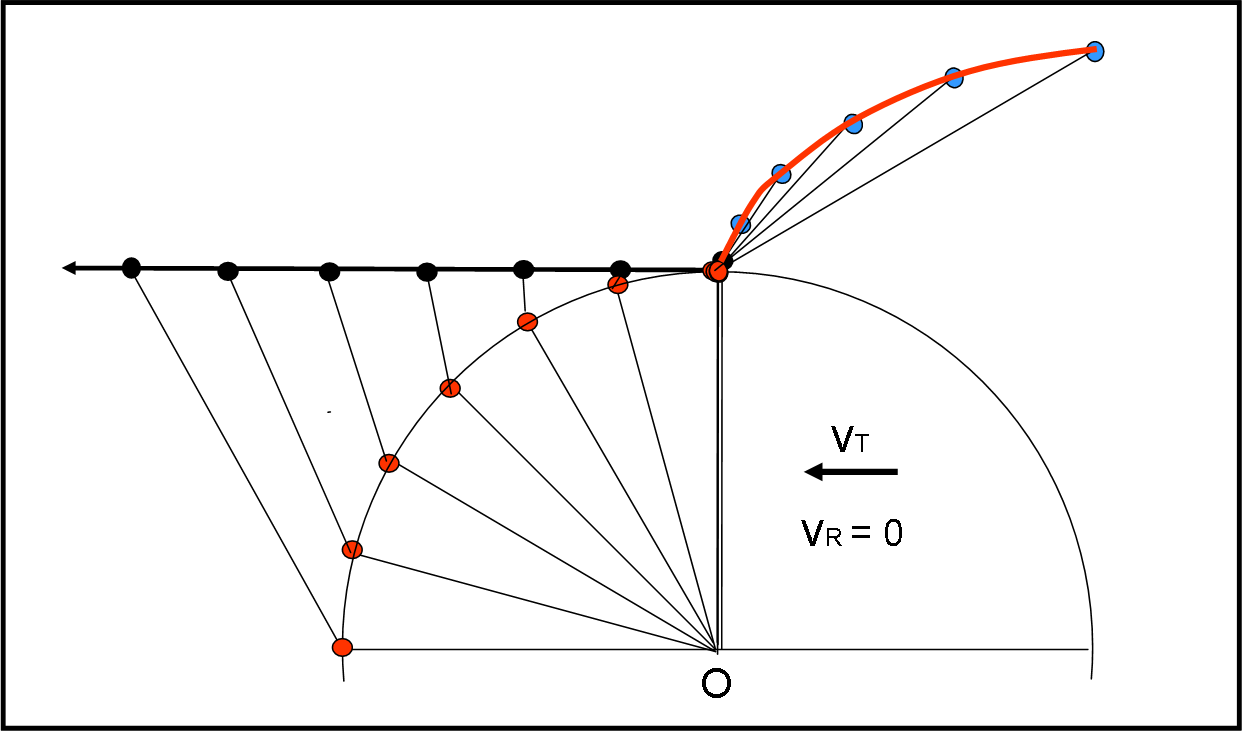
Mettiamoci al lavoro, utilizzando, ad esempio, l'ultimo metodo grafico usato e otteniamo pochi esempi illustrati nelle Fig. 28, 29, 30 e 31. Nella Fig. 28 la velocità è tutta tangenziale e ritroviamo perfettamente quanto ricavato col taglio della corda. L’aereo, ovviamente, se ne va verso l’esterno, come una pallina che segue la velocità tangenziale. L’angolo α è ZERO per entrambi i sistemi.
La Fig. 29 illustra un caso in cui l’aereo va veramente piano… Sembra quasi la traiettoria di prima, ma, se andiamo a “zoomare” sugli istanti iniziali, vediamo che l’aereo sembra fare un piccolo “giro” sopra l’aeroporto, per poi andarsene verso l’esterno. Quando l’aereo esce dalla piattaforma l’aeroporto si trova in A’ e quindi l’angolo α è praticamente zero o poco di più.
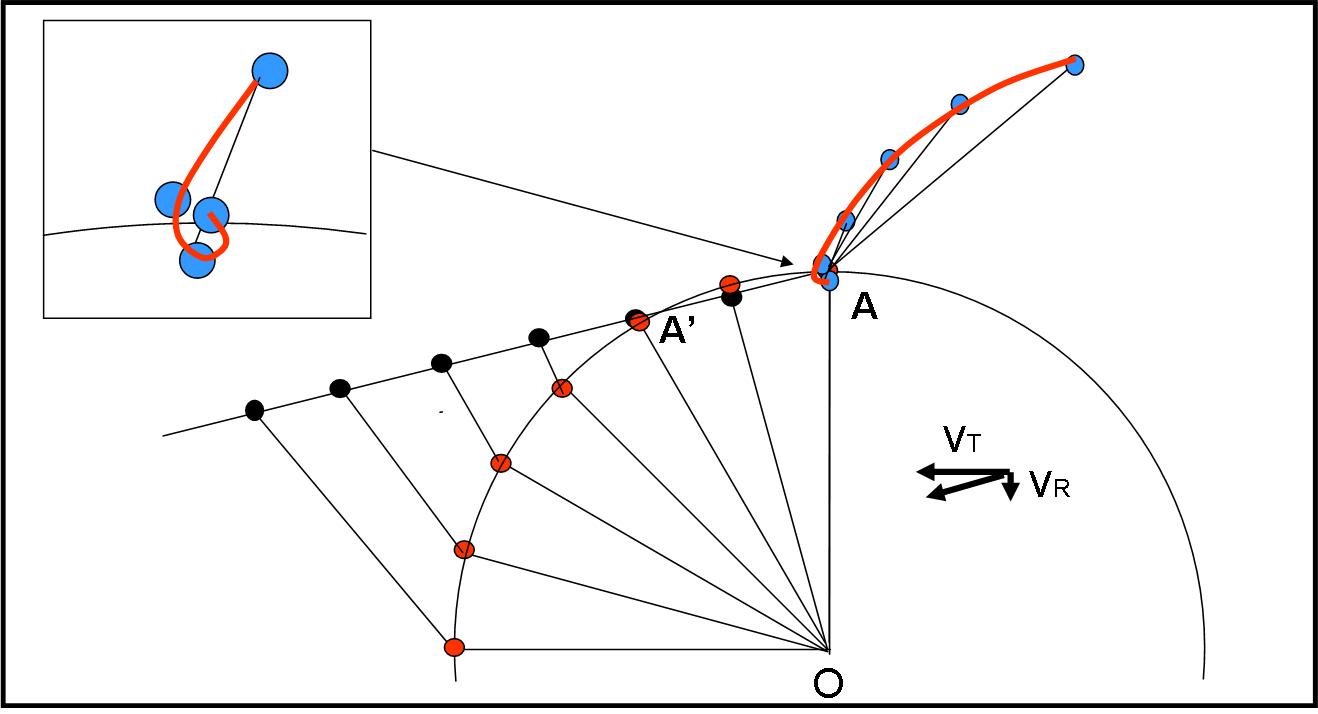
In Fig. 30 le cose si vedono molto meglio. Il giro sopra l’aeroporto si allarga e l’aereo esce dalla piattaforma quando l’aeroporto è arrivato in A’.
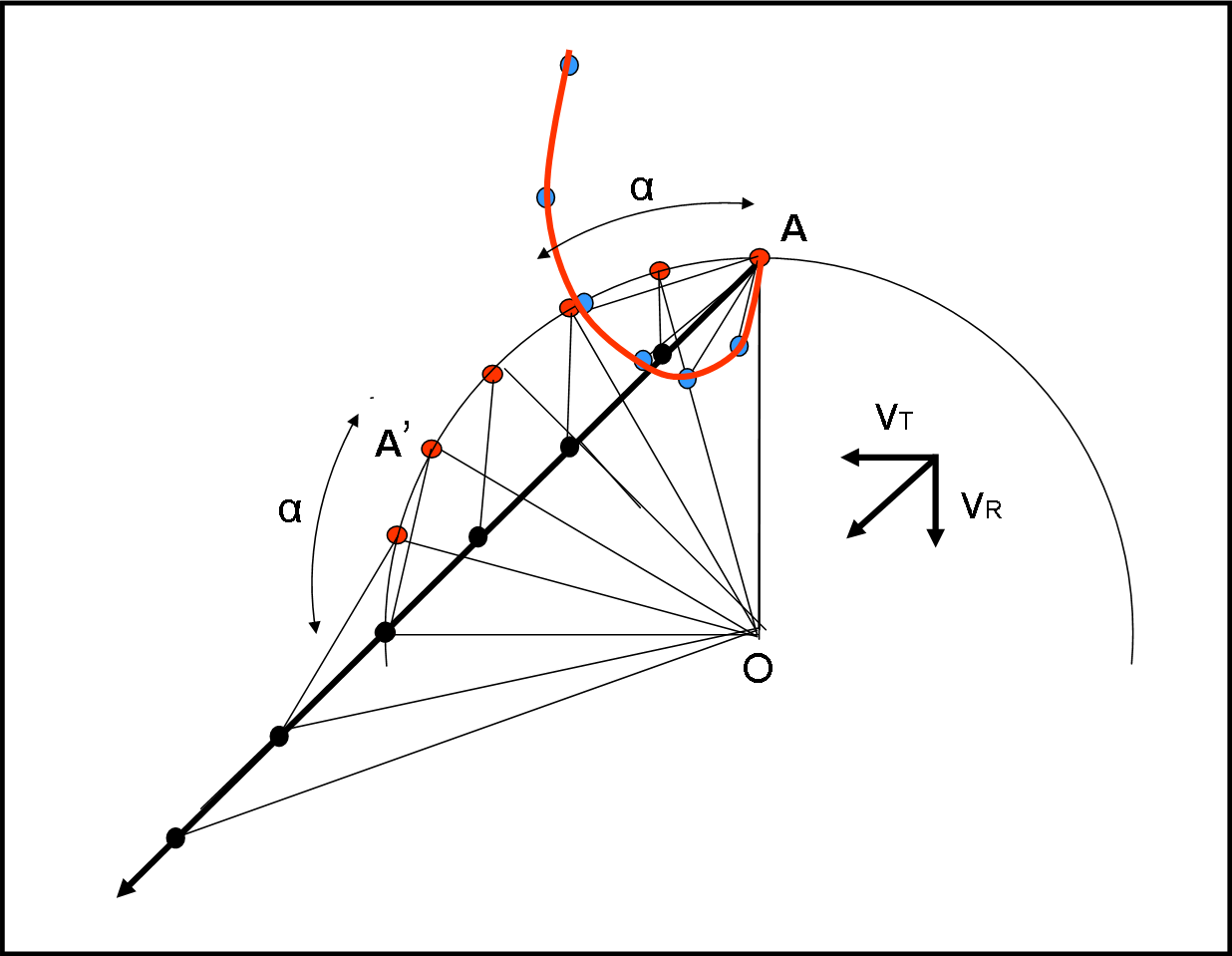
La Fig. 31 permette all’aereo di percorrere un discreto percorso prima di andarsene nello … spazio.
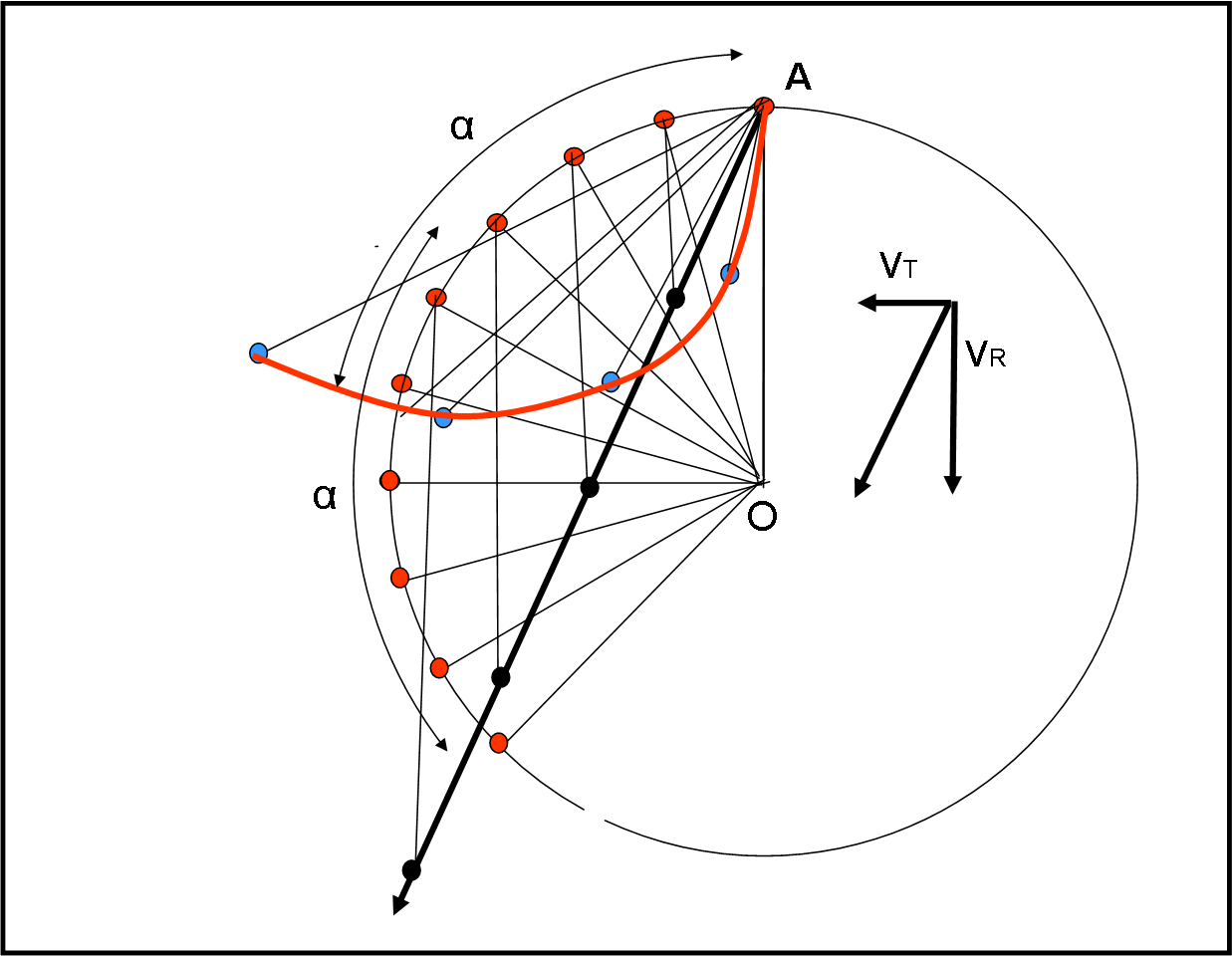
E via dicendo… come mostrato ancora meglio nelle animazioni di facilissimo utilizzo, preparate da Arturo. Un grazie di vero cuore!!!
Un problema "opposto".
Sul pianeta “Piattello” si è appena conclusa un’opera titanica: la costruzione di una bellissima autostrada che è riuscita finalmente a collegare direttamente il luogo equatoriale A (ricco e pieno di risorse) con il lontano Polo Nord, dove la popolazione vive di stenti, come mostrato in Fig. 32. Attraverso l’autostrada, questi ultimi potranno essere riforniti di tutto il necessario. Su Piattello non ci saranno più differenze tra ricchi e poveri!
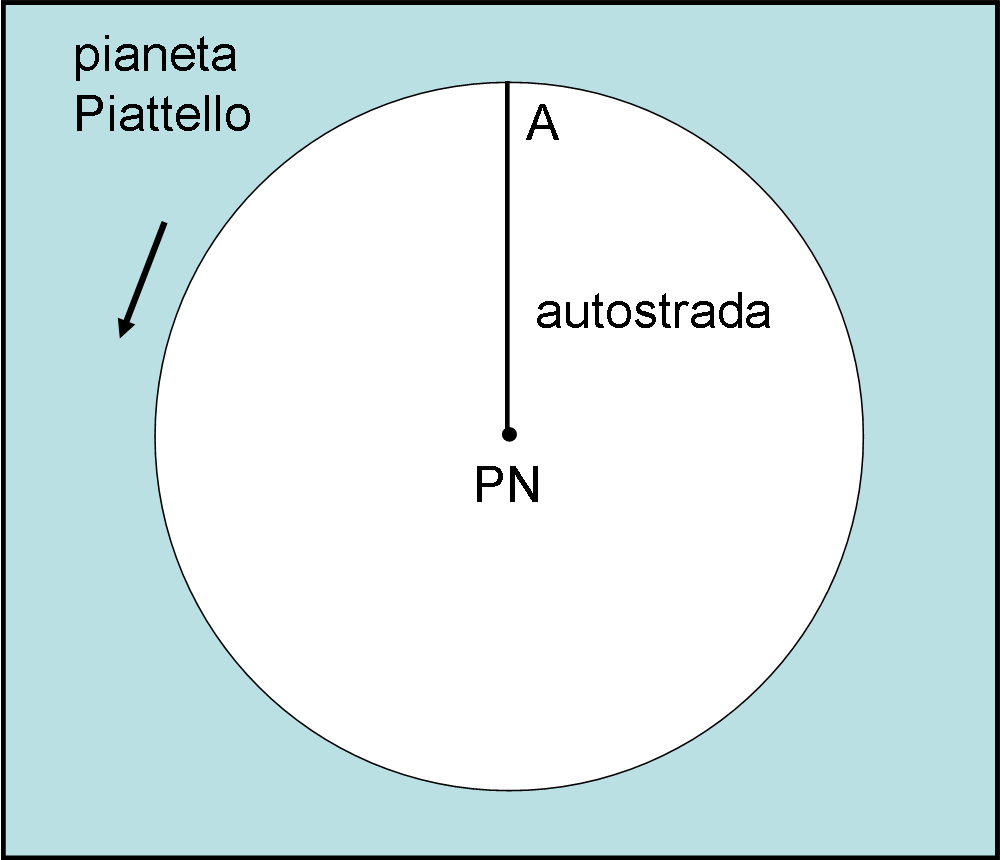
E’ il giorno dell’inaugurazione e un convoglio pieno di ogni ben di Dio parte a velocità costante da A per dirigersi a PN e poi tornare subito indietro per il secondo viaggio. E’ tutto illuminato e dallo spazio, anche a grandi distanze, è l’unica cosa che si riesce a vedere perfettamente.
In quello stesso istante, un’astronave aliena, alla ricerca di vita veramente intelligente e di spirito altruistico, lo osserva da molto lontano. Il pianeta (forse addirittura piatto) è appena percettibile e l’unica cosa che si riesce a vedere è una luce che si muove su di esso. L’astronave si ferma e osserva attentamente cosa sta succedendo. Quella luce è un fenomeno naturale o un fenomeno artificiale? E se fosse dovuta a una razza pensante, come sarebbe il loro carattere? Malvagio o fraterno (ne hanno visti di tutti i colori nel loro viaggio di ricerca).
Non passa molto tempo e sull’astronave si fa gran festa: esiste una razza intelligente e il loro spirito corrisponde perfettamente all’armonia dell’Universo. La luce ha descritto esattamente uno dei simboli universali di amore e fratellanza. Anche su Piattello si fa gran festa, dato che il viaggio di andata e ritorno si è concluso perfettamente.
L’astronave decide di scendere e sarà sicuramente accolta con la stessa loro gioia.
Sì, è vero… è tutto frutto di un caso fortunato, ma quello che conta è il risultato, che soddisfa entrambe le popolazioni così uguali nell’animo e così diverse nell’aspetto.
L’unico, trascurabile, problema è la fatica che ha fatto il convoglio, ma con la volontà si ottiene di tutto e di più, alla faccia di Coriolis.
Nel sistema rotante, il convoglio viene visto seguire la strada “dritta” anche se con un po’ di fatica (lui sente comunque le forze fittizie che agiscono su di lui, come quando fate una curva in macchina). Dal sistema inerziale la faccenda acquista una ben diversa visione. Il convoglio non va assolutamente dritto, ma fa un lungo percorso spiraleggiante che lo porta al polo!
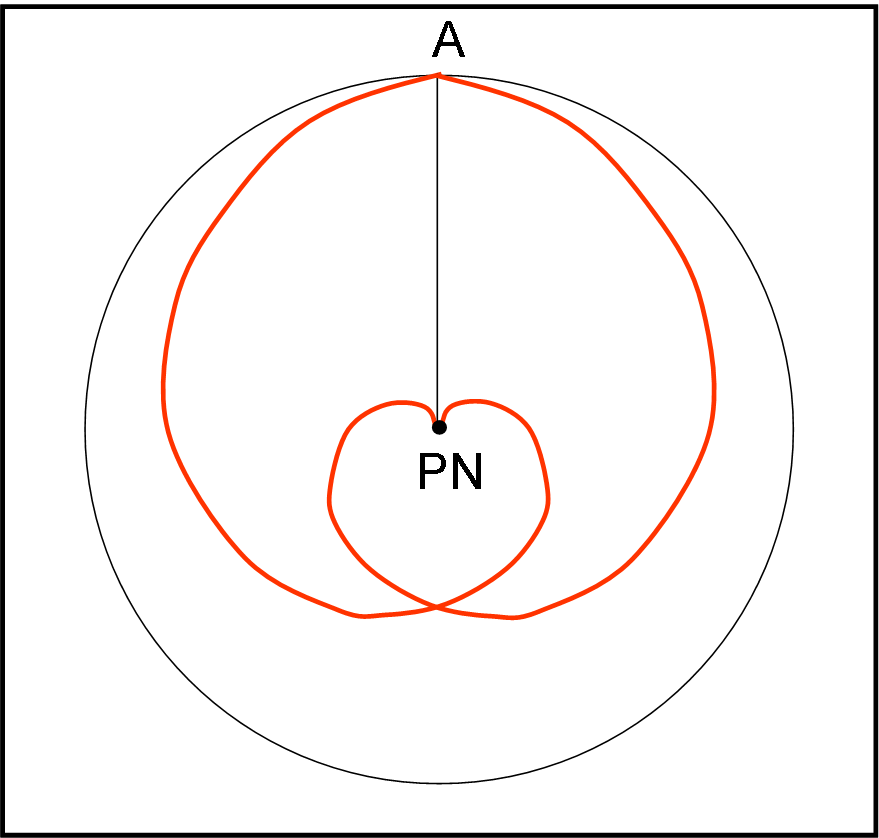
Oltre al moto percorso effettivamente nel sistema non inerziale si deve aggiungere il moto compiuto da tutto il sistema non inerziale. Qui non ci sono accelerazioni fittizie, ma solo accelerazioni vere; in particolare, quella centripeta che tiene il convoglio ancorato al suolo, come un lanciatore di martello che riduce sempre più la corda dell’attrezzo sportivo e viceversa. Per un’astronave, tra andata e ritorno si forma chiarissimo il simbolo del cuore ( anzi… due cuori!). Se il convoglio si fermasse nel suo moto verso il Polo, si assisterebbe, dal sistema inerziale, a un semplice moto circolare uniforme...
Inseriamo la Fig. 33 che mostra la figura vista dall'astronave
Un po' di serietà "fisica"
Tiriamo un po’ le somme, dopo i tanti esempi che abbiamo illustrato, per mettere in evidenza la forza di Coriolis e la cara sorella centrifuga. Va bene la semplicità grafica, ma un po’ di fisica non guasta mai. In particolare, dobbiamo capire bene quanto e come siano attive, in un vero gioco di squadra! Reputo, perciò, questo capitolo molto utile per legare insieme tutto quanto detto finora… non saltatelo!
E’ vero, abbiamo scherzato molto, tra un quiz e l’altro, con le traiettorie viste da un sistema inerziale e da un sistema rotante. E tutto ciò è servito solo e soltanto per potere applicare sempre e comunque le leggi della dinamica newtoniana. Non pensiamo, però di avere solo giocato… Le varie traiettorie ci dimostrano molto bene come le due accelerazioni fittizie (chiamiamole pure così) riescano perfettamente nel loro compito. Lavorando geometricamente le abbiamo trovate quasi automaticamente, ma sappiamo molto bene che esse si calcolano abbastanza facilmente anche attraverso un paio di derivate o poco più (ricordate l'inizio "matematico"). Cerchiamo di collegare con molta semplicità le due visioni, sapendo molto bene che il risultato deve essere sempre lo stesso.
La collaborazione tra l’accelerazione di Coriolis e quella centrifuga è decisamente molto fruttuosa. Ricordiamo, innanzitutto, che esse esistono solo nei sistemi non inerziali ed è proprio per questo che vengono chiamate “fittizie”. La centrifuga agisce quando cambia la distanza radiale (o per non farla cambiare, come nel moto circolare uniforme), mentre quella di Coriolis dipende essenzialmente dalla velocità con cui si muove l’oggetto. A volte predomina l’una, a volte l’altra, ma non possono fare a meno di lavorare in grande armonia e riuscire a riprodurre esattamente ciò che capita nel sistema inerziale.
Ricordiamoci della pallina tenuta in rotazione da una corda. Se la corda funziona, la pallina risulta ferma nel sistema rotante e l’unica accelerazione che si deve creare per questo scopo è quella centrifuga. Nel sistema inerziale basta invece quella centripeta (reale). A un certo momento, tagliamo la corda: per un sistema inerziale tutto è ovvio e facile: abbiamo di fronte una traiettoria rettilinea che conferma pienamente il principio d’inerzia. Come viene a mancare l’unica forza agente sulla pallina (quella centripeta), la pallina riprende il suo moto rettilineo e uniforme. Tutti i sistemi inerziali vedrebbero la stessa cosa.
Un sistema rotante, che vuole considerarsi fermo, deve accettare la stessa conclusione, ma per lui è molto più difficile darne una spiegazione. La sua stessa rotazione impone un movimento rotatorio alla pallina (quello che capita a lui, lo trasferisce alla pallina). Sì, andrebbe anche bene, ma il fatto è che per le leggi di Newton una traiettoria curva deve subire almeno un’accelerazione.
Ma una non basta, dato che mentre il sistema ruota, e vede la pallina viaggiare per la sua traiettoria, cambia continuamente anche la sua distanza dal centro di rotazione e ciò implica l’accelerazione che ben conosciamo, quella centrifuga.
Spostandoci su una piattaforma rotante e facendo muovere la pallina (senza attrito e senza forza di gravità) dal centro verso l’esterno, un modo estremamente indicativo per dimostrare la corrispondenza tra sistema inerziale e non inerziale è proprio l’angolo α, quello che indica dove l’oggetto esce dalla piattaforma. Esso deve restare lo stesso per entrambi i sistemi, dato che il fenomeno meccanico deve restare uguale.
Consideriamo proprio questa situazione, che è la più semplice e dove è più facile notare ciò che realmente succede, istante per istante. La configurazione è allora quella, ormai ben nota, della pallina che viene lanciata, con velocità costante e senza attrito, a partire dal centro di rotazione.
Guardando come evolve il movimento apparente, si possono capire i contributi delle due accelerazioni (o delle forze se introducessimo anche la massa della pallina).
Nel sistema inerziale (Fig. 34) tutto è di una semplicità quasi ridicola: la pallina si muove, ad esempio, di un metro al secondo mentre descrive la sua traiettoria verso l’alto, obbedendo alla legge di Newton.
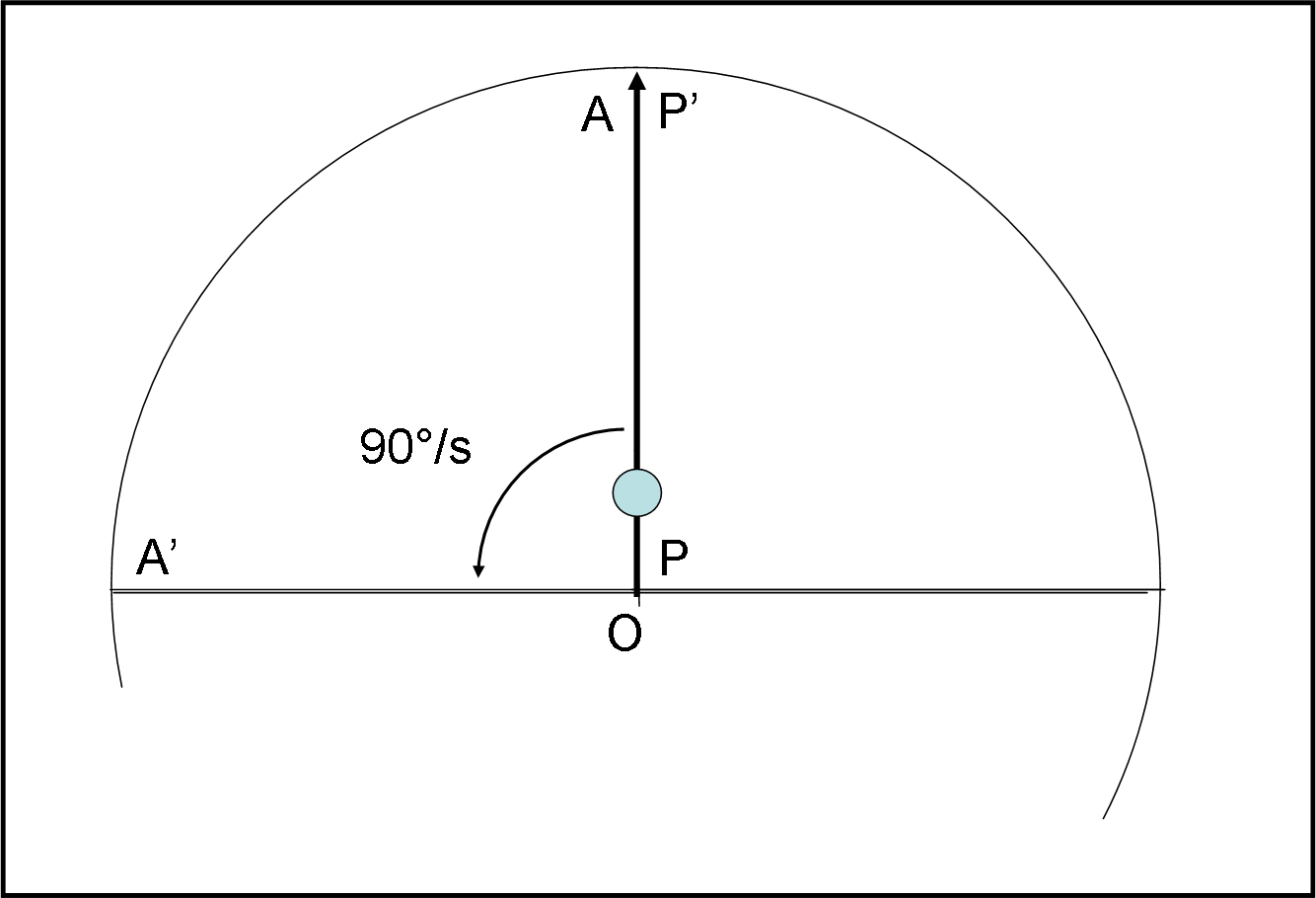
Se nessuna forza la viene a disturbare, lei continua in quel moto per l’eternità. Tuttavia, notiamo subito un risultato abbastanza sconcertante. La pallina, nel suo moto rettilineo, non può certo vietare alla piattaforma rotante di fare il suo mestiere (ad esempio ruotare di 90° al secondo). Quando arriva al bordo, il punto A che, al momento del lancio, si trovava proprio lungo la linea verticale del movimento della pallina, si è ormai spostato verso sinistra in A’. Tra la pallina P’, al momento dell’arrivo sul bordo, e il punto A’ si determina l’angolo α, dipendente sia dalla velocità della pallina sia dalla velocità di rotazione della piattaforma. Questo angolo α deve rimanere lo stesso anche quando l’osservatore si trova nel sistema rotante.
Spostiamoci, allora su di lui. Ciò vuol dire, essenzialmente, che il punto A si considera fermo e quindi coincide sempre con A’. Come conseguenza deve essere la pallina a subire un cambiamento di percorso per potere uscire in P’, alla stessa distanza angolare α, misurata precedentemente (Fig. 35)
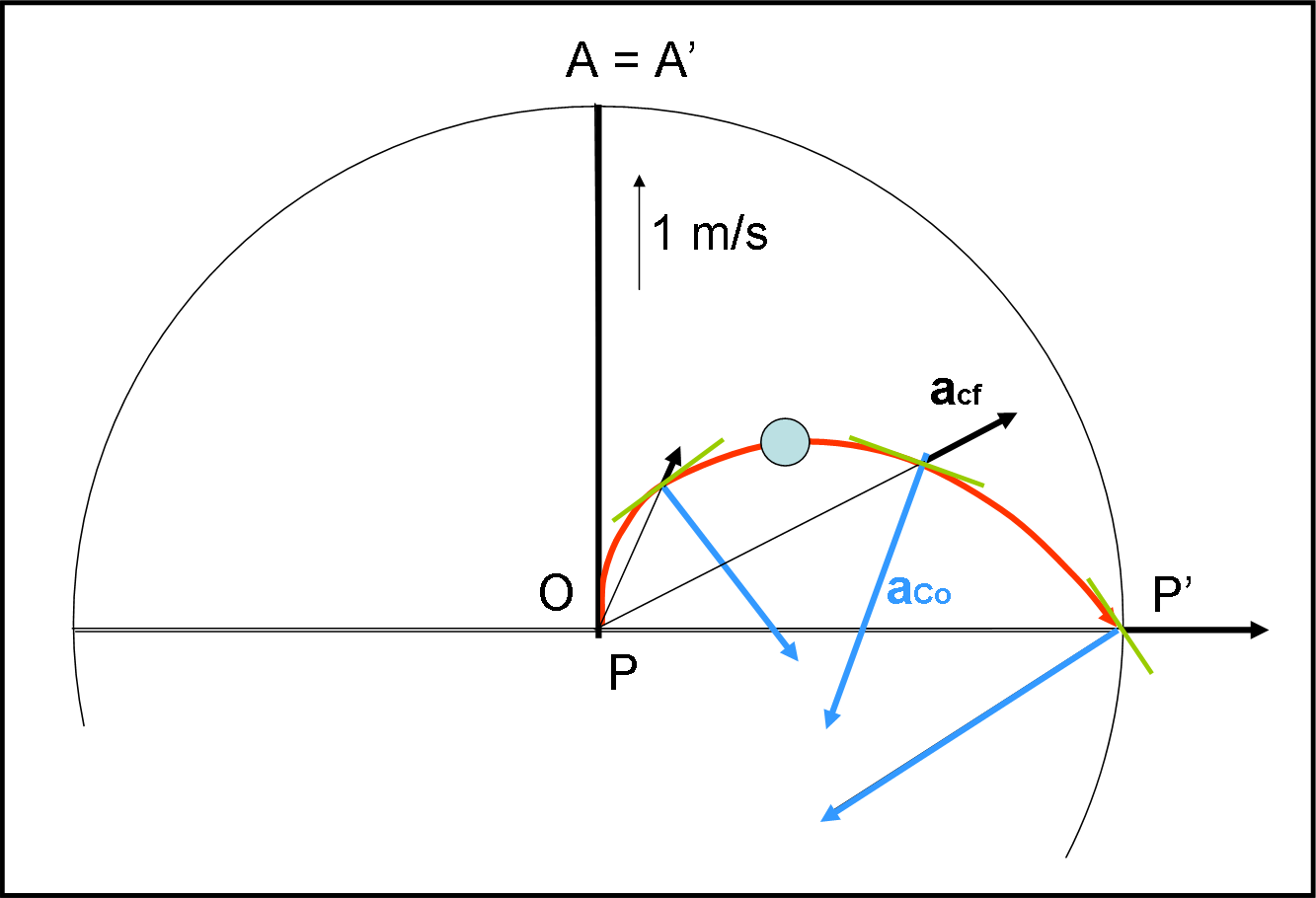
Le cose diventano più complicate. La pallina è costretta a descrivere un curva per poter confermare il fenomeno meccanico. Come già detto, ciò implica, secondo le leggi di Newton, che debbano intervenire ben due forze “fittizie” per ottenere il risultato cercato, ossia per confermare che nel sistema inerziale il movimento sia rettilineo e uniforme e che la pallina esca da P’. Un fatica non da poco, solo e soltanto per dare soddisfazione a quel genio di Newton…
Non è difficile disegnare la velocità nel sistema rotante, quella che ci ha permesso finora (utilizzando metodi grafici apparentemente diversi) di tracciare la traiettoria della pallina vista dal sistema non inerziale. In realtà, non abbiamo fatto altro che sommare la velocità costante e rettilinea del sistema inerziale a quella perpendicolare alla distanza della pallina dal centro (r’), che altro non è che la formuletta ricavata fin dall'inizio:
v’ = v – ω ∧ r’
v è proprio la velocità nel sistema inerziale, mentre il prodotto vettoriale regala quella perpendicolare alla congiungente il centro O con la pallina. Usate la mano destra, puntando l'indice (ω) verso l’alto, il medio in direzione di r’ e troverete che il pollice vi indica la direzione della velocità ω ∧ r’. Basta cambiare il segno e direzione e verso sono ricavati. Il modulo (visto che si lavora con angoli retti) vale proprio
v’ = v – ωr’
In tal modo (o graficamente come abbiamo fatto noi) posiamo determinare la traiettoria punto per punto o, ancora meglio, conoscendo la traiettoria della curva, determinare la tangente punto per punto. Conoscere la tangente, vuole dire conoscere la velocità (il modulo lo sappiamo) v’ nel sistema rotante. Siamo pronti, a questo punto, a disegnare le accelerazioni che agiscono in qualsiasi punto in cui si trovi la pallina.
Dalla poca matematica sviluppata, sappiamo quanto valgono le accelerazioni centrifuga e di Coriolis.
La prima vale:
aCF = - ω ∧ (ω ∧ r’)
Proviamo a girare due volte la mano destra e troviamo che questa accelerazione va sempre in verso radiale (ossia da O verso P). Essa, nel nostro caso semplificato, non ha bisogno di funzioni trigonometriche, è ha come modulo:
aCF = - ω2r’
Passiamo a quella di Coriolis, che ha come valore:
aCo = - 2(ω ∧ v’)
Conoscendo ormai v’ e avendo la mano destra ben allenata, si trova subito che essa è diretta in direzione perpendicolare alla tangente (velocità) istantanea.
Bene, disegniamo il tutto nella Fig. 35, ricordando che abbiamo imposto una velocità di partenza uguale a un metro al secondo e una velocità angolare di 90° gradi al secondo. Non ci vergogniamo certo di ragionare in modo quasi fanciullesco. Si vede bene come l’accelerazione di Coriolis tenda a spostare verso destra la traiettoria, mentre quella centrifuga tenda ad allungarla verso l’esterno. In parole molto semplici, vi è un continuo cambiamento della distanza r’, che comporta un’accelerazione centrifuga, e una continua variazione della direzione di v’ che comporta l’accelerazione di Coriolis. Entrambe dipendenti dalla rotazione del sistema non inerziale. Ripeto ancora: tutta questa fatica viene compiuta per far sì che il punto di uscita dalla piattaforma rotante coincida con quello trovato nel sistema inerziale.
In modo analogo, potremmo calcolare le accelerazioni, partendo dal bordo esterno e andando verso il centro, ricordando, però, che la traiettoria inerziale della pallina è sempre una retta, ma inclinata…
Una riflessione finale molto personale: non trattiamo male i sistemi non inerziali. Sembrano complicati, ma pensiamo alle strategie che devono usare per soddisfare i loro più fortunati amici inerziali. Inoltre, ricordiamo che solo i sistemi non inerziali sono capaci di piegare perfino la luce! E dico poco…
La Terra ruota... ce lo dice un pendolo!
Benché fin dall’antica Grecia (e forse anche prima) si ipotizzava, di tanto in tanto, una rotazione della Terra, nessuno era mai riuscito a dimostrarlo in modo così eclatante come con il pendolo di Foucault. L’unico modo per spiegare come mai un pendolo non mantenga fisso il proprio piano di oscillazione non può che essere la rotazione di quello che gli sta sotto, ossia l’intero pianeta.
Lo andiamo a studiare nei dettagli, dato che la forza di Coriolis gioca un ruolo fondamentale... però, prima, è necessario essere sicuri di una caratteristica del pendolo. Normalmente viene presa come un dato di fatto: il piano di oscillazione del pendolo è immutabile. Ci si può arrivare con semplici ragionamenti, ma, visto che abbiamo ripreso in mano i prodotti tra vettori, fatemi usare una dimostrazione molto pignola che fa uso dei prodotti scalari e vettoriali (di cui abbiamo parlato QUI). Farà un gran piacere agli amanti dei vettori e delle operazioni collegate.
Non vogliamo studiare a fondo il moto del pendolo, che può diventare anche piuttosto complicato. Tuttavia, per potere introdurre il pendolo di Foucault è quantomeno necessario averne una pur pallida idea.
In un sistema inerziale, sospendiamo una pallina P di massa m a un filo inestensibile fissato in O. Ipotizziamo che l’unica forza che agisca sulla pallina sia la forza di gravità FG = mg (g può essere considerata costante). Se la posizione è verticale la tensione del filo (Fc) equilibra perfettamente quella di gravità e la pallina è in equilibrio stabile (Fig. 36a). r è il vettore distanza tra O e la pallina P.
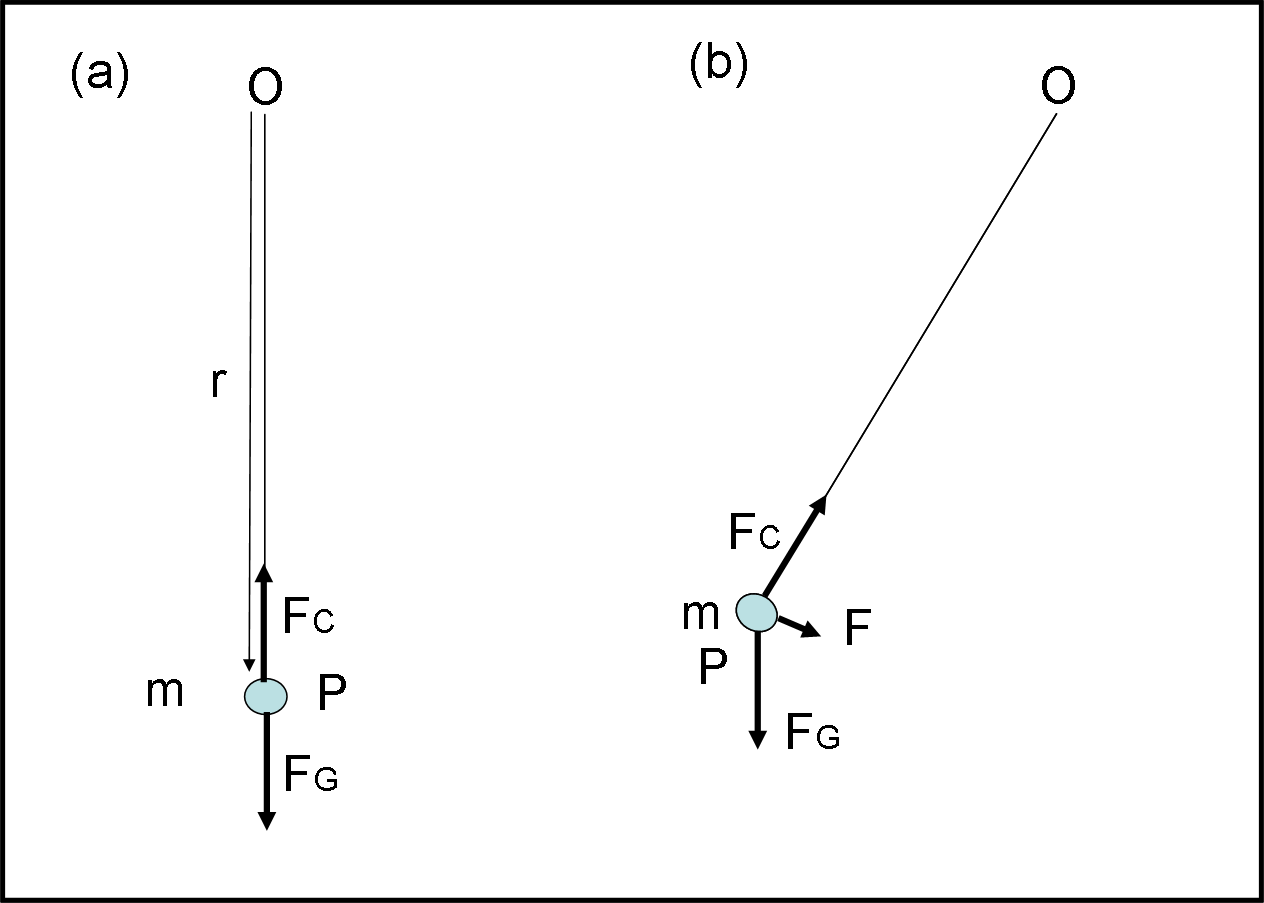
Spostiamo, adesso, la pallina P rispetto alla verticale, comunque si voglia, e lasciamola libera. Otterremo il ben noto moto del pendolo, dove la pallina raggiunge un altezza massima, con velocità uguale a zero, poi ricade verso il basso sorpassando la posizione di equilibrio verticale e risale nella direzione opposta fino a un’altezza uguale a quella di prima, e via dicendo, in assenza di attriti vari (Fig. 36b).
Il moto del pendolo viene spesso usato per descrivere la conservazione dell’energia, dato che nel punto più alto l’energia cinetica è zero (v = 0), mentre è massima quella potenziale. Nel punto più basso (posizione verticale) l’energia potenziale è minima, ma è massima quella cinetica e via dicendo, un po’ come nelle montagne russe.
Le uniche forze in gioco sono quella di gravità e la tensione del filo che non è altro che una forza centripeta. Normalmente, si dice che per questa ragione il moto deve avvenire esattamente nel piano individuato dalle due forze. La conclusione sembrerebbe ovvia, ma sapete che spesso i matematici sono un po’ paranoici e vorrebbero la garanzia che spostando la pallina in qualsiasi posizione rispetto a quella di equilibrio verticale si ottenga sempre e comunque un piano di oscillazione invariante.
Prendiamolo, perciò, come un giochino vettoriale, molto utile per sveltire la mano destra e per ricordare anche il prodotto scalare. Le formule sono semplicissime e basta solo un minimo di ragionamento.
Dalla seconda legge di Newton sappiamo che:
F = ma
Nel pendolo semplice, come già detto, sulla pallina P, di massa m, agiscono solo due forze: quella di gravità (mg) e la reazione del filo (forza centripeta) Fc.
Possiamo allora scrivere che l’unica forza agente è la somma vettoriale delle due forze reali (siamo in un sistema inerziale).
F = ma = Fc + mg
m dv/dt = Fc + mg …. (1)
Consideriamo adesso il vettore definito dal prodotto vettoriale r ∧ g (perpendicolare al piano contenente r e g) e moltiplichiamo scalarmente entrambi i membri della (1) per lui:
m dv/dt × (r ∧ g) = Fc × (r ∧ g) - mg × (r ∧ g)
Ricordiamoci che il prodotto scalare è uno scalare che si annulla quando i vettori sono perpendicolari tra loro (nel modulo compare il coseno). Il prodotto vettoriale, invece, è un vettore che si annulla quando i vettori sono paralleli tra loro (nel modulo compare il seno).
Per costruzione sia Fc che g sono perpendicolari a (r ∧ g) e quindi i prodotti scalari del secondo membro devono valere ZERO. Ne segue:
m dv/dt × (r ∧ g) = 0
La massa non è zero e quindi abbiamo:
dv/dt × (r ∧ g) = 0 …. (2)
Consideriamo, adesso, l’espressione:
d(v × r ∧ g)/dt = dv/dt × (r ∧ g) + v × (dr/dt ∧ g) + v × (r ∧ dg/dt)
Tuttavia, v non è altro che dr/dt, per cui il vettore (dr/dt ∧ g) deve essere perpendicolare a v; da che ne consegue che il prodotto scalare deve annullarsi. Inoltre, g può essere considerata costante per cui anche l’ultimo termine va a zero. Otteniamo, perciò, ricordando la (2), che:
d(v × r ∧ g)/dt = dv/dt × (r ∧ g) = 0
Ne segue che v × r ∧ g = costante
Tuttavia, nei punti di inversione del moto del pendolo la velocità deve essere zero per cui deve essere uguale a zero anche la costante.
v × r ∧ g = 0
da cui segue che i tre vettori devono essere complanari!
Infatti, r ∧ g non è uguale a zero e, quindi, per ottenere zero, v deve essere perpendicolare a questo vettore, ossia stare nel piano dei primi due.
Bene, adesso siamo sicuri che il piano del pendolo è un invariante e che, quindi, quando lo trasferiamo in un sistema non inerziale, è tutto il piano che subisce le forze apparenti.
Un pendolo al Polo Nord
Vorrei sfidare chiunque, che sia giunto esattamente al Polo Nord, a dimostrare che la Terra non sia piatta. Soprattutto se può muoversi di solo pochi metri attorno all’asse polare (ultimamente lo hanno dipinto di rosso per ricordare che il clima terrestre è ormai veramente “bollente”). Toccando l’asse polare (non muovetelo troppo, mi raccomando…) si avverte, però che, anche se piatta, la Terra gira attorno a quell’asta che punta quasi perfettamente verso la stella polare (le farà mica il solletico?).
Se siete raccomandati o se avete molti quattrini, potreste anche eliminare per un po’ di tempo l’asse polare vero e proprio, dato che la Terra ha una sua autonomia e continuerebbe a girare anche senza di lui. Al suo posto, potreste sistemare un ben pendolo che vi siete portati da casa e montarlo, seguendo istruzioni molto accurate che evito di enunciarvi. L’importante è che il filo del pendolo sia posizionato esattamente lungo l’asse terrestre. La sfera terminale è in grado di far scendere lentamente della polvere finissima di carbone. Poi, non vi resta che ricordare la piattaforma rotante e quella forza malandrina di Coriolis insieme alla sua degna compare centrifuga.
Finiamo di fare gli … idioti e parliamo più seriamente, facendoci aiutare dalla Fig. 37, dove la piattaforma piatta IMMOBILE (vincolata perfettamente alla superficie terrestre in quella piccola zona) è vista dal punto di sospensione del pendolo S. La sfera con la polvere sia P, in condizioni di equilibrio, ossia esattamente lungo la verticale del filo. Tutto è immobile o, almeno, sembra… (a parte un orso bianco in piena forma, inseguito da ambientalisti che vogliono misurargli la febbre a tutti i costi…).
La faccenda, se non si considera il filo del pendolo, sembra esattamente quella che ci è servita varie volte per evidenziare le forze fittizie nella piattaforma rotante. Questa volta, però, non abbiamo bisogno di far ruotare la piattaforma, dato che essa gira insieme alla Terra attorno all’asse di rotazione individuato da P e/o S. Il suo moto è, ovviamente, in senso antiorario, e compie un giro completo in 24 ore. Non è una grande velocità angolare, ma sufficiente a causare effetti ben visibili sul moto della sfera P, una volta che il pendolo sia stato messo in moto.
Basta, ora, lasciare libertà all’orso bianco e permettergli di dare il via al pendolo per fargli compiere il proprio mestiere, lasciando una traccia scura sulla piattaforma, mentre si muove da un estremo all’altro di essa, seguendo le regole che abbiamo descritto parlando del piano invariante.
L’orso è molto interessato (è riuscito a disperdere gli ecologisti assatanati) e si mette in azione. Dopo 24 ore, è veramente soddisfatto dalla figura che ha visto descrivere dal pendolo e vuole provare di nuovo, ma, questa volta, osserva un disegno leggermente diverso.
Ah… un certo Foucault si trovava di passaggio da quelle parti e ha rubato l’idea all’orso bianco… senza dargli alcun compenso…. E poi diceva di essere un amante degli animali …
La spiegazione di ciò che ha fatto e visto il nostro orso bianco è molto semplice: messo in moto nelle condizioni più favorevoli, esso non può che proiettare una linea retta sulla superficie della piattaforma, andando avanti e indietro. Tuttavia, la piattaforma ruota insieme alla Terra attorno al polo, da cui segue che la traccia di polvere lasciata dal pendolo non può mai essere la stessa. Però, ci sono almeno due modi per far oscillare un pendolo...
In fondo, è quello che abbiamo già trovato lasciando libera una pallina di attraversare, con una certa velocità rettilinea una piattaforma girevole. Nel sistema di riferimento rotante il percorso della pallina è tutt’altro che rettilineo. La stessa cosa deve capitare anche alla traccia lasciata dal nostro pendolo polare. Proprio il fatto che la linea sia curva ci impone la presenza della forza centrifuga e di quella di Coriolis.
Se esso viene mosso (senza imporgli strani spostamenti iniziali) quando è in condizioni di equilibrio (filo verticale e sfera immobile), il moto del pendolo è veramente rettilineo nel sistema inerziale (Fig. 38b) e siamo nel caso trattato in cui la pallina parte senza velocità intrinseca.
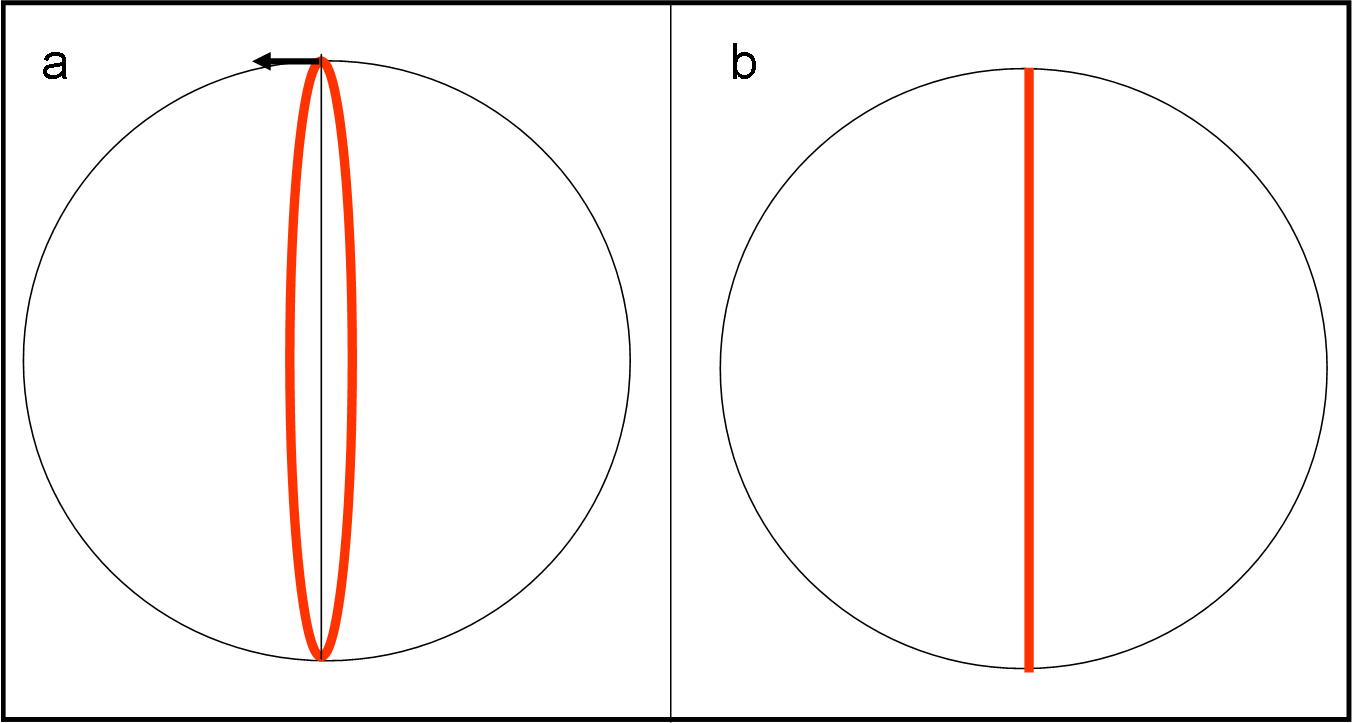
La figura che ne segue (Fig. 39b) è una specie di fiore con tanti petali (la quantità dipende dalla velocità del pendolo rispetto alla velocità di rotazione).
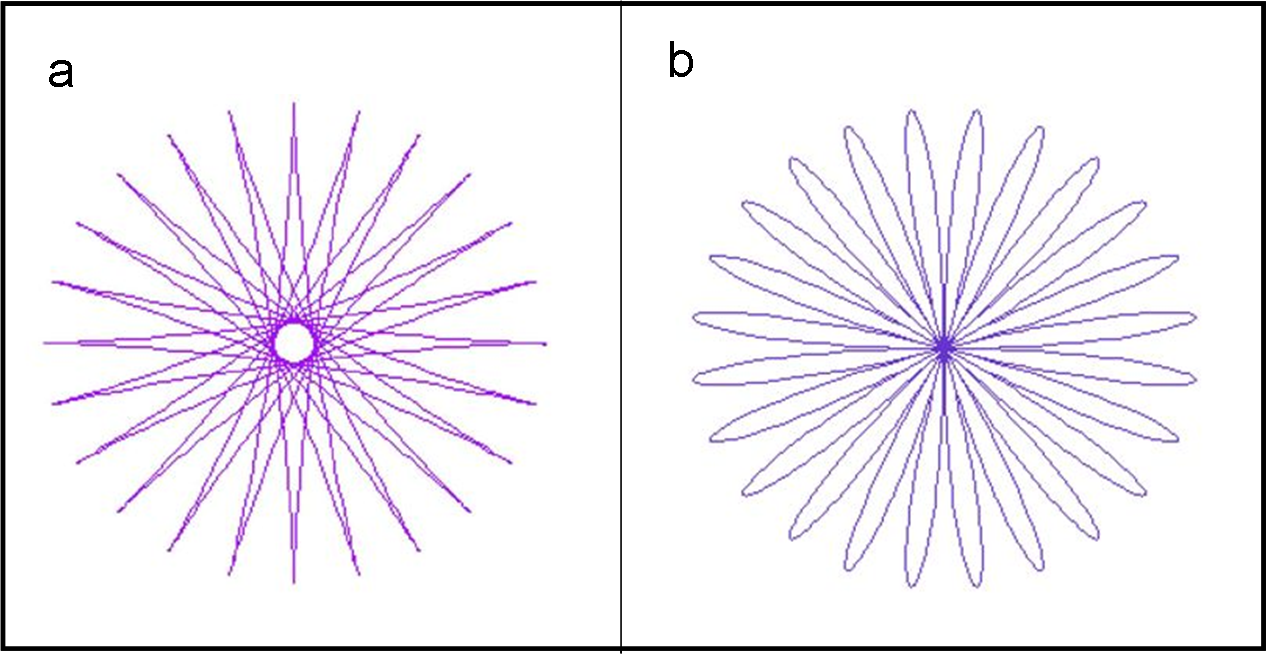
Essendo partito dal punto centrale, ogni traccia lasciata dalla sfera deve passare per tale punto. La costruzione geometrica del “fiore” viene mostrata in Fig. 40.
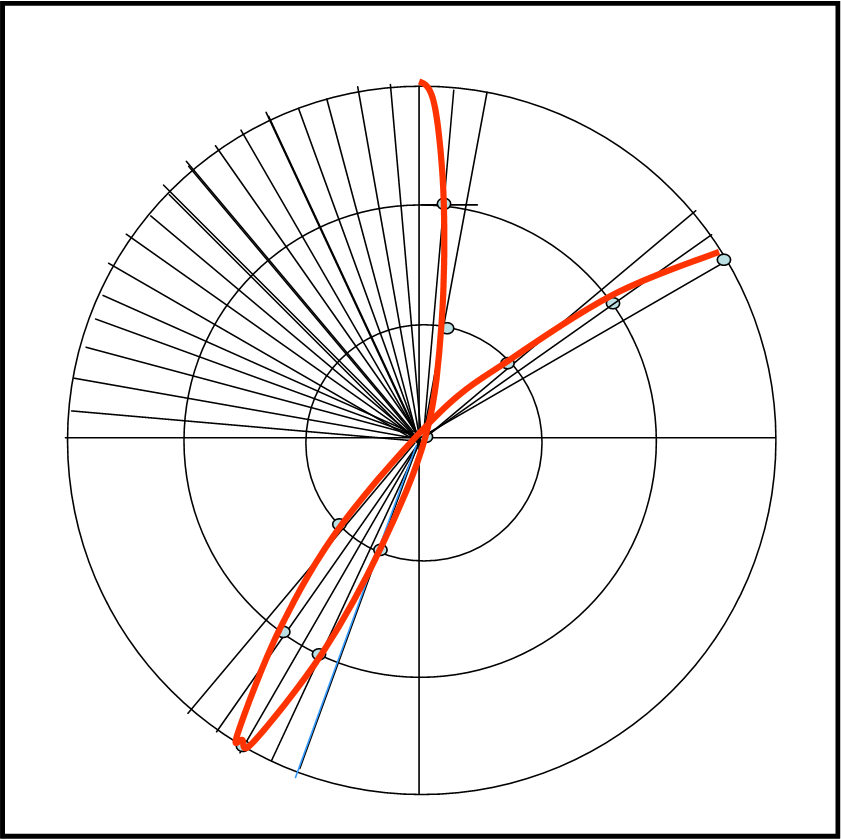
Il pendolo, però, può anche iniziare il suo percorso ponendo la sfera a una certa altezza dalla piattaforma. Anche se l’orso la lascia libera senza dare scossoni laterali, è indubbio il fatto che la sfera si trovi a una certa distanza dall’asse polare e quindi debba conservare la velocità tangenziale che ha anche l’orso (principio d’inerzia).
Tuttavia, la sfera non è libera di proseguire lungo la linea che si ottiene sommando la velocità di attraversamento della piattaforma e di quella tangenziale, dato che è pur sempre vincolata al punto di sospensione: il filo non è estendibile e mantiene sempre la stessa lunghezza. Siamo di fronte a una specie di pendolo conico, e -senza entrare in dettagli inutili- la traiettoria descritta dalla sfera lascia come traccia un’ellisse (nel sistema di riferimento inerziale) (Fig. 38a), che si trasforma in tante linee curve che danno luogo a una specie di stella, con tante punte, nel sistema rotante (Fig. 39a). Si può notare che la traccia non passa mai per il centro, ossia per il punto di equilibrio stabile.
Il video che segue (già proposto dal nostro amico Andy) mostra i due casi in modo perfetto.
A questo punto, prima di spostarci dal polo e lasciare il nostro orso a divertirsi con chissà quanti altri movimenti più che bizzarri, è forse giusto ribadire un concetto che a volte può creare un po’ di confusione: “In pratica, cosa vede un alieno al di fuori del sistema rotante della Terra? Vede una traccia sempre uguale o vede proprio crearsi un po’ alla volta le figure descritte precedentemente?”. Ovviamente la risposta giusta è la seconda!
Ricordiamoci sempre che il fenomeno fisico deve rimanere lo stesso: cambia solo il modo di spiegarlo!
A mano a mano che la polvere cade dalla sfera, la piattaforma si muove sotto di lei e quindi l’alieno non può che vedere una traccia curva. Tuttavia, per lui la motivazione è proprio quella VERA, ossia un qualcosa di rettilineo (o lievemente ellittico), nel suo sistema, lascia una traccia curva dato che il “foglio da disegno” continua a cambiare posizione. Non solo, ma anche i due tipi di figura hanno un senso reale. In un caso il pendolo parte da fermo e non ha velocità trasversale al moto, mentre nell’altro il pendolo parte con una leggera velocità trasversale che deriva alla rotazione di chi lo ha in mano prima di lasciarlo.
L’orso bianco, invece, si considera fermo e per spiegare quelle strane curve lasciate dalla sfera è obbligato a introdurre delle forze fittizie che agiscano su di lei.
Per completare la trattazione dovremmo descrivere cosa succederebbe se il pendolo non fosse più appeso al polo nord (o sud), ma in un luogo qualsiasi della Terra (a latitudine φ). E’ cosa ovvia che il pendolo continui a oscillare tranquillamente in un unico piano se lo portassimo all’equatore, dove il vettore velocità angolare della Terra è perpendicolare al filo del pendolo (Fig. 41).
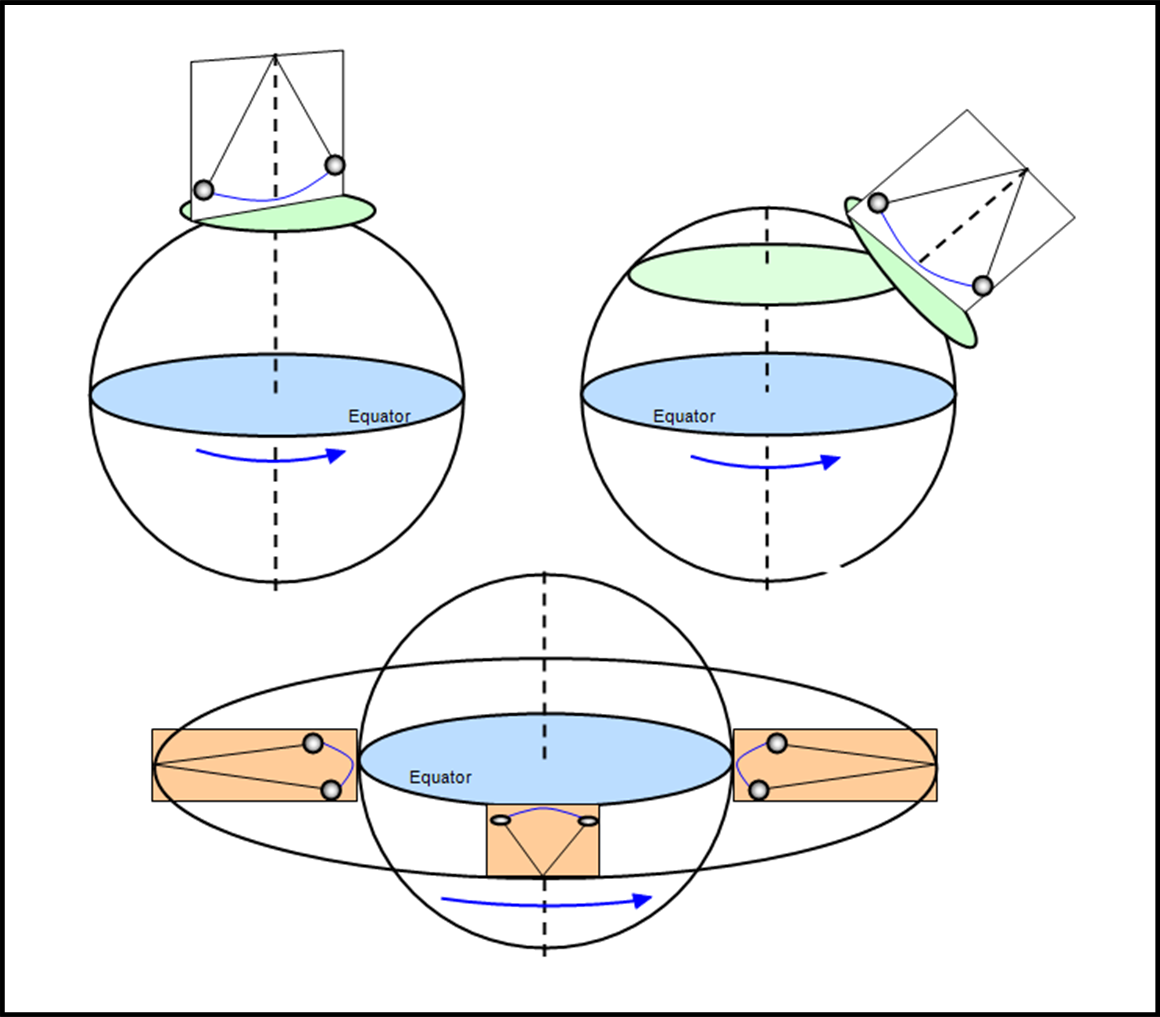
Più complicata è la faccenda per una latitudine qualsiasi. La cosa migliore sarebbe esprimere compiutamente l’equazione del moto del pendolo, ma vi assicuro che non è cosa semplice (un po’ come risolvere l’equazione del moto dei due corpi). Direi proprio di evitarla e limitarci a poche considerazioni di facile comprensione.
Basta poco per rendersi conto che più la latitudine φ diminuisce e più è lungo il tempo necessario al pendolo per completare la sua figura.
Se il punto di sospensione non appartiene all’asse terrestre, ma si trova alla latitudine φ, la velocità angolare ω ha una componente radiale ω sin φ e una componente tangente al meridiano, Fig. 42.
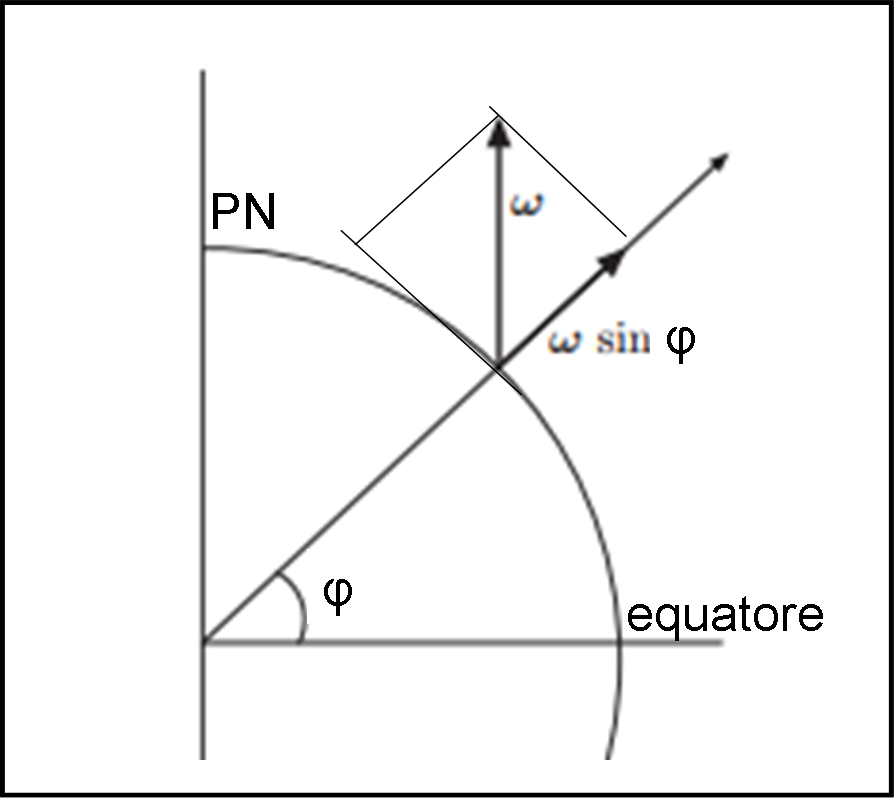
Quest’ultima, per piccole oscillazioni è inefficace. Dunque, alla latitudine φ, il piano di oscillazione del pendolo ruota attorno ad un asse verticale con velocità angolare ωφ = ω sin φ.
Possiamo, allora, scrivere, chiamando Pφ il periodo di rotazione completa del pendolo:
ωφ = 2π/Pφ = ω sin φ = (2π/P) sin φ
1/ Pφ = sin φ/P
Pφ = P/sin φ = 24h/sin φ
Per φ = 90°, otteniamo Pφ = P (polo)
Per φ = 0°, otteniamo Pφ = 1/0 = infinito
Attenzione agli uragani
Vediamo di concludere la nostra lunga trattazione sulla forza di Coriolis, abbandonando palline, astronavi, aerei e, perfino, pendoli. La nostra piattaforma rotante è diventata tutta la Terra e vogliamo studiare, in modo molto divulgativo, l’effetto più vistoso della forza di Coriolis (e di sua sorella centrifuga). Stiamo parlando dei vortici ciclonici e anticiclonici. I primi, soprattutto, causano i celebri cicloni con i loro effetti devastanti. Purtroppo, la forza di Coriolis ha un peso non indifferente sulla creazione di questi tragici fenomeni atmosferici.
Cerchiamo di spiegare, in modo molto schematico e semplificato, come ciò possa avvenire, facendo tesoro di quanto abbiamo imparato finora.
In Fig. 43 possiamo disegnare la superficie terrestre e localizzarci su una fascia intermedia, tropicale.
Seguiamo il viaggio di quattro particelle o di goccioline d’acqua. Esse ruotano solidalmente con la Terra, se non vi sono forze esterne a modificarne il moto. Immaginiamo, adesso, che in un certo punto dell’emisfero nord terrestre vi sia un centro L di bassa pressione. Non voglio certo inserirmi negli studi del nostro amico farfallino, perciò mi limito a dire che le quattro particelle si “staccano” dal legame terrestre e iniziano a muoversi senza attrito (in prima approssimazione) verso la depressione. Possiamo dire che esse vengono spinte dal vento. A noi, meccanici puri, questa situazione ci dice soltanto che vi sono quattro palline che si stanno muovendo su un sistema rotante.
Per capire meglio la situazione guardiamo la Terra dal Polo Nord (Fig. 44).
E’ facile notare che la particella A sta scendendo verso l’equatore (ossia verso il bordo esterno della nostra ben nota piattaforma girevole), mentre la particella B sta salendo verso il Polo Nord. I nostri grafici (e le nostre poche formule) ci dicono subito cosa vedrebbe un osservatore nel sistema terrestre rotante: esso vedrebbe piegare misteriosamente le due particelle, entrambe verso destra rispetto alla direzione del moto. La colpa, per lui è dell’accelerazione di Coriolis e di quella centrifuga. Ovviamente, la stessa cosa deve succedere per un osservatore inerziale (il solito alieno in visita). Per lui non è molto difficile spiegare il tutto con le leggi di Newton. La particella che parte dal basso conserva la velocità tangenziale di rotazione che si somma a quella verticale, da cui nasce la curva che vede percorrere dalla particella B. Analogamente vede la particella A che si stacca dal sistema rotante con un velocità tangenziale molto piccola (addirittura nulla se partisse dal polo). La conclusione è comunque la stessa: la particella percorre una curva spostata verso destra rispetto al moto ventoso. In fondo è ciò che abbiamo notato e studiato parlando di astronavi e aerei e anche del pendolo di Foucault.
In molti testi ci si ferma qui, dato che le due tracce curvilinee, con tanto di freccia, fanno già pensare a una rotazione delle particelle in senso antiorario (nell’emisfero nord). Tracciando linee ventose più o meno inclinate rispetto al centro depressionario la struttura assumerebbe sempre meglio la tipica forma del ciclone. Già a questo punto si possono dire due cose ovvie: se invece di un centro depressionario, vi fosse un centro di alta pressione, le particelle scapperebbero in direzione radiale e la rotazione finale sarebbe di tipo orario. Esattamente il contrario capiterebbe nell’emisfero meridionale.
Facciamo ancora notare, sempre che ce ne sia bisogno, che il vortice si vede sia nel sistema rotante che nel sistema inerziale (come nel pendolo di Foucault). Infatti il fenomeno fisico deve essere lo stesso e le particelle che si muovono lasciano un chiaro segno sulla superficie terrestre così come faceva la polvere nel pendolo mosso dal nostro orso bianco (tra parentesi continua a stare molto bene, anche se si sta lamentando un pochino del freddo… sapete, è un fautore del GW…).
Tuttavia, pur restando a un livello estremamente semplificato, e ricordando che entra in gioco la gravità terreste, possiamo ancora migliorare la forma del nostro vortice ciclonico. Facciamo passare un parallelo attraverso il centro depressionario. A questo punto consideriamo le particelle C e D che si muovono proprio lungo il parallelo. La particella C sta andando più veloce di un punto stazionario sulla Terra e quindi tende a “decollare” ossia a portarsi più in alto, avendo una forza centripeta maggiore. Tuttavia, la gravità terrestre non le permette certo di uscire impunemente dall’atmosfera e allora la nostra particella deve cercare una posizione che competa alla velocità acquisita. La cosa migliore da fare è spostarsi verso l’equatore (ossia verso destra) in modo da vivere in pace con la sua velocità maggiorata. Il processo contrario capita per la particella D che va in senso contrario al moto terrestre. Essa è costretta a diminuire la sua velocità e tenderebbe ad andare verso il suolo. Tuttavia, una soluzione molto più “fisica” e semplice è quella di spostarsi verso una zona dove la sua velocità è quella “normale”. Essa si sposta verso latitudini maggiori, dove la velocità è minore. In altra parole, ancora verso destra e il vortice si realizza perfettamente, come possiamo notare bene nella Fig. 45. A sinistra un vortice costruito tenendo conto anche di altri fattori legati all’atmosfera, a destra un vero ciclone tropicale.
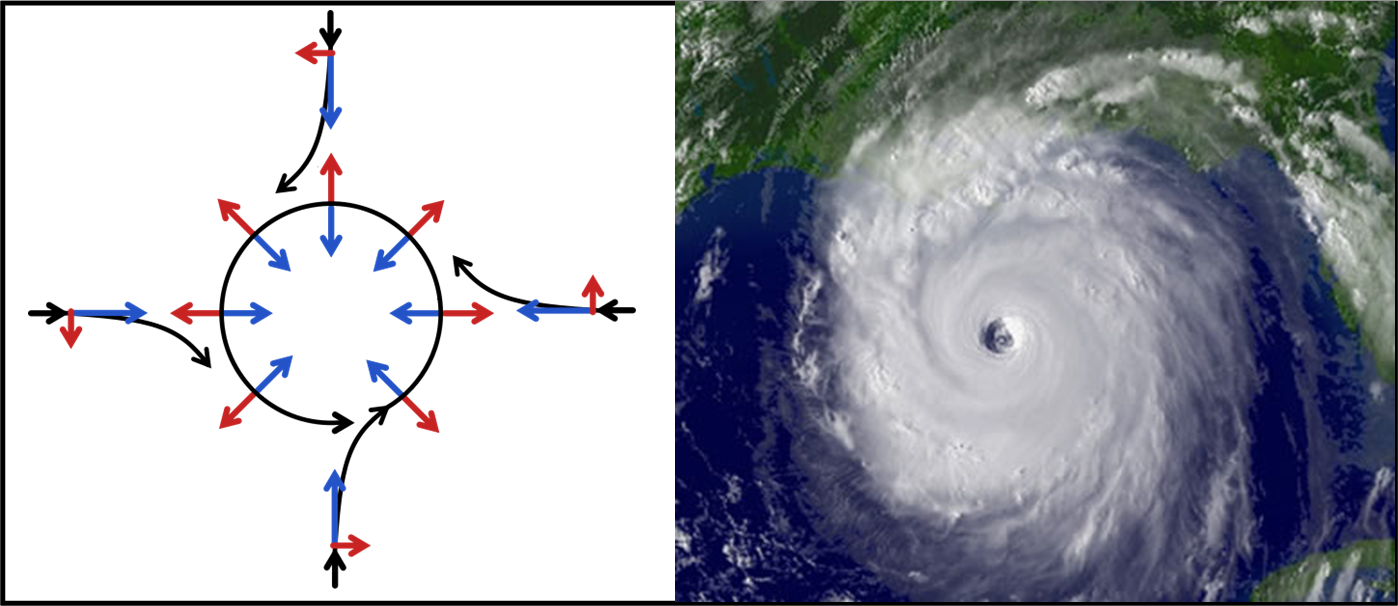
Possiamo fin da subito concludere con una notizia un po’ triste (ma non ditelo ai grandi degustatori di vino come Vin-Census! ![]() ): per ottenere strutture così vistose e impressionanti sono necessari venti e tempi decisamente notevoli. Niente di tutto ciò può quindi avvenire negli scarichi dei lavandini (o in un bicchiere di vino…)! La rotazione dell’acqua dipende dalla forma e dalle condizioni di partenza. Inoltre, essendo un fenomeno che attira molto i turisti, spesso si costruiscono scarichi adatti allo scopo e si impara facilmente a versare l’acqua nel modo … giusto.
): per ottenere strutture così vistose e impressionanti sono necessari venti e tempi decisamente notevoli. Niente di tutto ciò può quindi avvenire negli scarichi dei lavandini (o in un bicchiere di vino…)! La rotazione dell’acqua dipende dalla forma e dalle condizioni di partenza. Inoltre, essendo un fenomeno che attira molto i turisti, spesso si costruiscono scarichi adatti allo scopo e si impara facilmente a versare l’acqua nel modo … giusto.
Prima di terminare, dobbiamo ricordare ancora qualche effetto della nostra forza così misteriosa e così semplice e attiva.
Il primo è quello relativo alla caduta dei gravi che ha permesso a Guglielmini di provare (anche se lasciando parecchi dubbi) la rotazione della Terra 60 anni prima di Coriolis. Per saperne di più basta andare a leggere questo divertente e istruttivo articolo di Maurizio. In poche parole, il discorso è sempre lo stesso: un oggetto viene lasciato cadere da una torre molto alta e si trova in caduta libera. Tuttavia, mantiene la velocità tangenziale che aveva a quell’altezza. Scendendo si porta ad altezze alle quali corrispondono velocità sempre minori. Quando arriva a Terra si troverà spostato verso est, in quanto la sua velocità originale che si è conservata gli ha permesso di anticipare la rotazione del suolo terrestre. Una spiegazione più che sufficiente. Tuttavia, ricordiamoci che un corpo in caduta libera, nel sistema di riferimento terrestre, subisce anche la forza di Coriolis (movimento da una zona esterna della piattaforma rotante verso il centro). Ne segue che l’interpretazione corretta dell’esperimento di Guglielmini è ben più complessa di quanto possa sembrare.
Più immediato è l’effetto sulle rotaie di un treno… Se una tratta Nord-Sud (o Sud-Nord) viene percorsa sempre nella stessa direzione, il binario di destra sarà più consumato, in quanto la forza di Coriolis tende costantemente a deviare il treno verso destra. Questo caso è quello trattato QUI parlando del pianeta Piattello e del convoglio che collega equatore e Polo Nord.
Analogamente, provate a camminare su un tram mentre sta girando: se gira a sinistra vi sentirete sbattere verso destra, così come capiterebbe su una città spaziale rotante (il caso cui abbiamo parlato QUI - figura 18).
Direi che ci possiamo fermare qui, sperando che la forza di Coriolis non abbia più segreti per i lettori.


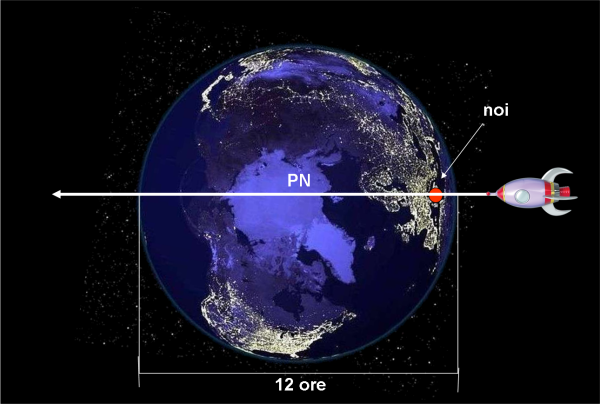




25 commenti
A proposito della forza di Coriolis, è vero che gli scarichi del lavandino girano in senso orario o antiorario a seconda se si è nell'emisfero boreale o australe, mentre invece all'equatore non vortica affatto?
Ho trovato questo articolo sul sito della National Geographic:
http://www.nationalgeographic.it/scienza/2017/12/14/news/che_cos_e_la_forza_di_coriolis_sapevatelo-3791372/
E' vero oppure è una bufala???
cara Allegra,
mi stupisco che NG possa dire simili sciocchezze! Le dimensioni del lavandino e la velocità di caduta fanno sì che i valori in campo non riescono assolutamente a mostrare l'effetto Coriolis. Quello che conta è la forma del lavandino e il modo con cui l'acqua viene fatta cadere. Lo sanno bene quelli che fanno vedere ai turisti questo effetto cambiare quando si è a cavallo dell'equatore. Per potere ottenere qualcosa di percepibile bisognerebbe avere enormi serbatoi in condizioni di stabilità ultra perfetta. Comunque, alla fin dell'articolo lo dico chiaramente...
Ad inizio anno scorso sono stato raggiunto da due carissimi amici e su loro richiesta, trovandoci nell'emisfero sud, abbiamo deciso di verificare la forza di Coriolis. Riempito il lavandino, abbiamo aspettato che l'acqua fosse in quiete, messa un poco di schiuma sopra per evidenziare l'effetto e quindi tolto il tappo. Il gorgo per tre tentativi consecutivi si è messo a girare in senso antiorario.
Tirando le conclusioni su quanto osservato abbiamo stabilito di aver preso atto della forma del lavandino e siamo passati alla birra.........
NG solo e soltanto un'americanata non stupirti più di tanto Enzo, basta che sprechi qualche ora a guardare il loro canale per convincerti.
Forse hai proprio ragione, caro Frank... chi fa più divulgazione veramente seria?????
Uno lo conosco, un tal Prof. Zappalà. Mi pare sta dalle tue parti.
Scherzi a parte, se proprio si vuole fare un confronto la BBC sta su un'altro livello e anche la RAI con alti e bassi, contemporaneamente, qualche cosa di buono lo fa. Ammetto che sono proprio bravi a nasconderlo. Ad esempio RAI storia.
Ci rimane la birra.........di Coriolis.
caro Frank... Rai Storia è proprio uno dei pochissimi canali che seguo e a volte ci sono "pezzi" veramente belli e seri. Comunque sì, vengono ben nascosti, magari in terza o quarta serata... meglio che la gente comune non li guardi... non si mai, potrebbe anche cominciare a pensare con la propria testa...
P.S.: se hai ancora problemi con la marea, dimmelo e preparo una figura ancora più evidente...
Quindi, non ho capito, quel video che fanno vedere ai turisti è una bufala? Come anche ciò che vediamo nei nostri lavandini?
Cara Allegra, mi sa che quelli del National Geographic sono più scherzoni del sottoscritto, però non sono originali né divertenti come Vin-Census... guarda qui http://www.infinitoteatrodelcosmo.it/2017/01/21/la-vera-storia-di-vin-census-3-il-vino-e-coriolis/ cosa è stato capace di inventarsi quando ha avuto voglia di scherzare con Coriolis!
Guarda anche tu, Frank, se per caso non lo hai già fatto! Non sarà birra, ma...
cara Allegra,
non penso proprio che NG volesse scherzare (Scherzy si diverte sempre a divertire...). Purtroppo le bufale scientifiche che ci propinano sono ben più grandi degli effetti di Coriolis (pensa al GW...). Ti posso assicurare che hanno fatto esperimenti "ad hoc" per studiare fino a che punto si potrebbe rilevare l'effetto in un lavandino. Ci vuole una perfezione assoluta, una vasca enorme di acqua perfettamente immobile e un caduta ultra controllata. Ma anche così non vedresti certo girare il tutto come un ciclone. Provo a cercare l'esperimento (i) e te li metto in evidenza... Anzi, no... se non credi a me, puoi andare anche su wikipedia (forza di Coriolis) e alla fine si parla parecchio dei lavandini... Una volta tanto una voce di wiki italiana abbastanza ben fatta...
Vincenzo, intanto auguri di buon anno, stavo leggendo questo dettagliato ed interessantissimo tuo articolo sule forze "fittizie" e sulla forza di Coriolis. Nella prima parte si legge
______
Se il moto, invece, è anche rotatorio, le cose si complicano dato che la derivata di un versore u (è ancora di modulo unitario, ma cambia direzione e verso) è un nuovo versore perpendicolare al primo. In particolare si dimostra che:
du/dt = ω Λ u …. (5)
Dove ω è il vettore velocità angolare (regola della mano destra, ricordate…).
Per ottenere questa semplice relazione, basta dimostrare che la derivata di un versore (non costante in direzione e verso) è sempre un versore (unitario come modulo) ma con direzione perpendicolare al primo.
Facciamo il prodotto scalare di due versori ortogonali:
(u X u) = u2 = costante
d(u x u)/dt = d(u2)/dt = 0
ma la derivata si può anche scrivere:
d(u x u)/dt = u x du/dt + u x du/dt = 2 u x du/dt
Tuttavia, sappiamo che la derivata deve essere uguale a ZERO, da cui segue che
2 u x du/dt = 0
Ossia:
u x du/dt = 0
Ma se il prodotto scalare di due versori di modulo costate è uguale a zero essi devono essere perpendicolari. Ossia, se la rotazione (ω) avviene attorno a un’asse perpendicolare a entrambi si ha proprio che du/dt può essere scritto come la (5):
du/dt = ω Λ u .
______
Tutto chiaro ma la mia domanda è questa, forse è banale, perché si deve ricorrere al prodotto scalare di due versori per dimostrare che la derivata di un versore rispetto al tempo è un vettore perpendicolare ai due vettori. Si deduce, è vero, che se il prodotto scalare di due vettori è nullo i due vettori sono perpendicolari.
Applicando il prodotto scalare a u x u = cost = 1 come fatto e derivando il prodotto si evince che il vettore u è perpendicolare alla sua derivata d u /dt.
Perché si deve ricorrere la prodotto scalare per dimostrare ciò, è un procedimento prettamente matematico?
Ma, Michele... è proprio quello che viene fatto... non capisco bene cosa proporresti...
se u è un versore, come faccio a dire, in altro modo, che du/dt è perpendicolare a u ?
Si è cosi Vincenzo a volte purtroppo mi pongo degli interrogativi non logici (forse colpa dell'età).
D'altra parte una giustificazione geometrica di ciò potrebbe essere questa (correggimi se sbaglio):
Moto circolare uniforme
il raggio vettore r ruota intorno al centro con velocità angolare ω costante
al tempo t sia r(t)
al tempo (t+ dt) sia r(t)+ dt
la differenza geometrica tra i due vettori r(t+ dt) - r(t) si ottiene applicando la regola del parallelogramma
per la posizione al limite ovvero per dt → 0 che è data dal limite de l rapporto incrementale per dt → 0
il vettore differenza risulta tangente alla circonferenza di raggio r e quindi ⊥ a r(t)
ottima considerazione, caro Michele...
L'astronave che tu hai descritto Vincenzo quella che inizia il suo viaggio con velocità costante partendo da sopra la verticale al "punto Italia" vista da un sistema di riferimento esterno alla terra e considerato fisso inerziale percorre una traiettoria rettilinea che congiunge il "punto Italia" con il punto polo nord. In realtà l'astronave se attraversa l'atmosfera terreste sarebbe soggetta anche alle forze di attrito con la stessa e sarebbe un po' trascinata dal moto rotatorio della terra e dalla sua atmosfera, questo non accadrebbe se la sua altezza dal pianeta fosse tale da non trovarsi nella sua atmosfera. Il caso teorico rappresentato e senza dubbio molto istruttivo per capire le differenze rispetto ai sistemi di riferimento inerziali e quelli rotanti. Certamente se l'astronave avesse fatto il suo viaggio sopra la Luna passando sopra un ipotetico punto "Italia Luna" e dirigendosi in linea retta verso il polo nord della Luna il viaggio visto dal punto Italia Luna coinciderebbe qualitativamente con quello descritto.
Questo articolone Vincenzo è veramente eccezionale, non l'avevo letto prima, ma debbo convenire che spiega in maniera dettagliata ed esaustiva gli argomenti sui sistemi di riferimento e sulle forze "fittizie" da considerare nei sistemi non inerziali in particolare per quanto riguarda la forza di CORIOLIS che non sempre viene descritta in modo comprensibile ed esaustivo
grazie Michele! era stato molto faticoso, devo dire...
Finalmente di questo Coriolis ci ho capito qualcosa dopo che mi aveva sempre lasciato con dell'amaro in bocca. Una bella donna che mi sembrava sempre di essere lì lì per conquistare, ma che ogni volta sentivo in qualche modo sfuggirmi.
Vi racconto una curiosità in merito alla figura 33. In aeronautica l'identità curva viene detta "rotta del cane" perché è il percorso che fa un cane per raggiungere il cibo inseguendone l'odore in presenza di vento. Ovviamente un bravo pilota deve evitarla in quanto più lunga. Immaginate che in presenza di vento laterale dovete raggiungere un radiofaro puntandogli direttamente il muso, cioè seguendo la direzione della lancetta dello strumento (ADF) che vi indica da dove proviene il segnale radio. Vi trovereste a percorrere la rotta del cane fino ad arrivare sul radiofaro esattamente controvento. Il bravo pilota invece corregge e ricorregge già da subito la direzione di qualche grado a destra, se il vento viene da destra, o viceversa, a seconda della sua intensità.
Non c'entra con Coriolis, ma vi assicuro che seguendo in tal modo i radiofari, i piloti sanno portare il loro aereo dall'equatore al polo nord, dritti, dritti :-)
grazie Alberto, per ulteriori informazioni sempre utili a tutti noi!
Gentile Vincenzo,
interessante articolo.
Le chiedo una delucidazione.
Nei testi di Meccanica Razionale e di Fisica io trovo indicato che - ω ∧ (ω ∧ r’) è l'accelerazione DI TRASCINAMENTO (che è centripeta, il segno meno indica che è diretta verso l'asse di rotazione) e fa sorgere sulla massa, in rotazione, la forza di TRASCINAMENTO che è di verso opposto, CENTRIFUGA.
Quindi perchè mi scrive aCF = - ω ∧ (ω ∧ r’) e il modulo aCF = - ω2r’
Lo stesso vale per l'accelerazione di Coriolis: io trovo nei testi che è espressa come 2(ω ∧ v’) e non aCo = - 2(ω ∧ v’) e provoca una forza deviante, di verso opposto all'accelerazione.
caro Marco,
non è importante il segno, dato che dipende da quale verso considero come positivo, ma il fatto che centrifuga e centripeta hanno segni opposti.
Certo, dipende dal verso di riferimento: ma una volta fissato un verso di riferimento l'accelerazione centrifuga dovrebbe essere di verso opposto alla accelerazione di coriolis (veda la fig. 35). E' per questo che non mi trovo con la fig. 35. aCF dovrebbe essere ω ∧ (ω ∧ r’)
Mi spiace Marco, ma tutto mi sembra corretto...
Si, si è tutto corretto, aCF = - ω ∧ (ω ∧ r’).
Solo che se eseguo il doppio prodotto vettore di - ω ∧ (ω ∧ r’) mi risulta aCF = ω2r’, mentre nel suo testo trovo scritto che il modulo di aCF = - ω2r’ e non mi trovo quindi nel raffronto con aCo = - 2(ω ∧ v’) che ha il segno meno: in fig. 35 i due vettori sono in opposizione circa, come giustamente ha disegnato.
Grazie e complimenti per tutto.
Marco
Forse siamo in argomento. Pongo un quesito.
Sono su una giostra vicino all'asse di rotazione ed osservo due masse uguali collegate tra loro da un cavo lungo l munito di dinamometro. Le masse sono disposte radialmente in modo che il centro del cavo di collegamento stia sull'asse di rotazione. Un morsetto lo blocca alla piattaforma girevole. Conosciamo la velocità di rotazione w.
Il dinamometro indica una forza centrifuga F pari a m*(l/2)*w^2.
Eliminiamo ora il morsetto. La forza che tende il cavo non è più originata dal centro della giostra distante l/2 ma dalle due masse, che diventano interagenti e distano l. La forza centrifuga sulle masse non cambia perché l'accelerazione è la stessa, ma quanto segna adesso il dinamometro? Ancora F oppure un altro valore?
Michele
come sai, caro Michele, non sono un tecnologo. Non capisco bene, comunque, se le due masse continuano a essere collegate tra di loro oppure no...
Le masse continuano ad essere collegate.
Io faccio un ragionamento forse troppo semplicistico. L'equilibrio nel moto rotatorio rispetto al centro di rotazione si ottiene per F*(l/2) = m*v^2. Una volta eliminato il morsetto la rotazione avviene tra una massa e l'altra e quindi per F'*l = m*v^2 = F*(l/2) e quindi per F' = F/2. Sembra che i conti non tornino.