Che cos’è il tempo proprio? E’ il tempo che intercorre tra due eventi misurato dall’orologio di chi si muove lungo la linea di Universo che collega i due eventi. Il tempo proprio è il tempo misurato da chi sta nel sistema visto in movimento.

L’osservatore sul treno, che contiene l’orologio di luce, misura gli intervalli di riflessione con un solo orologio. L’osservatore che sta sul marciapiede necessita invece di due orologi, dato che l’orologio di luce si sposta nello spazio. Quest’ultimo vede il tempo sul treno dilatarsi.

Da queste poche frasi, legate strettamente alla simultaneità, si giunge subito al nocciolo del problema. Se l’osservatore del sistema S vede due eventi separati nel tempo e nello spazio non può assolutamente misurare un tempo proprio. Ha, infatti, bisogno di due orologi, posti nei due luoghi spaziali. Misura il tempo proprio solo il sistema S’ in cui non vi è differenza di spazio tra i due eventi. Il sistema S’ è proprio quello che il sistema S vede viaggiare a una certa velocità tra i due eventi.

E’ quindi necessario che per S’ le coordinate spaziali dei due eventi A e B siano uguali.

Scriviamo l’intervallo di spazio (usiamo solo la coordinata s) nel sistema S’ attraverso le trasformazioni di Lorentz, quelle che legano le coordinate dei due sistemi di riferimento:

s'_B - s'_A = ((s_B - s_A) – v (t_B - t_A))/(1 - (v/c)²)^1/2

La prima cosa da determinare è la velocità v  di S’ nel sistema S. Si ricava rapidamente, dato che sappiamo che s'_B - s'_A  = 0 (il tempo proprio si ottiene solo nel sistema che non si muove)

Con i dati del problema, possiamo scrivere:

0 = 3.6·10⁸ – 2 v

(il denominatore non può essere mai zero)

v = 3.6·10⁸/2 = 1.8·10⁸ m/s

Da cui

v/c = 0.6

Risulta immediato il valore di γ

γ =  1/(1 - (v/c)²)^1/2 = 1.25

1/γ = 0.8

Conoscendo il tempo improprio

t_B - t_A = 2 s

Ricaviamo il tempo proprio

t’_B – t’_A  = 2 /γ = 2 · 0.8 = 1.6 s

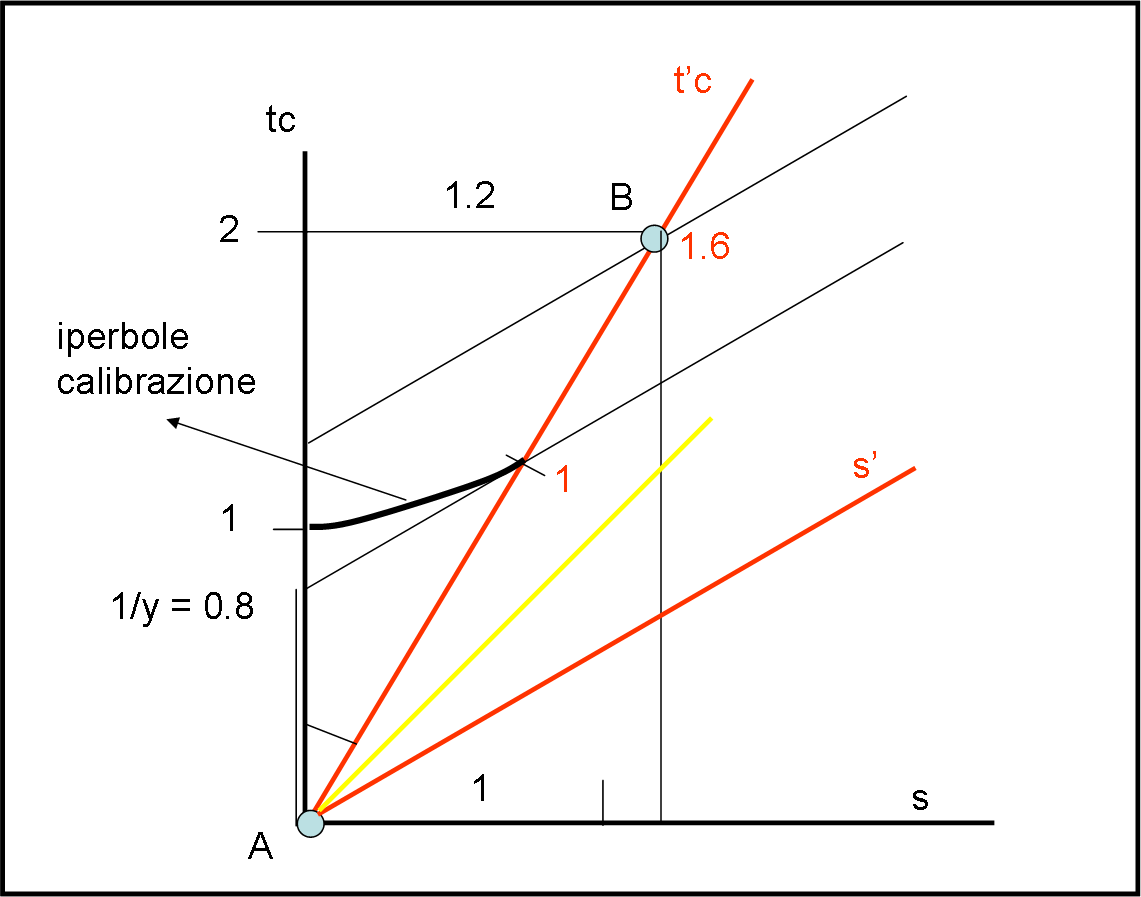
L’intera faccenda la possiamo rappresentare facilmente utilizzando il diagramma di Minkowski, come mostra la figura che segue

Penso che per chi ha seguito la RR, la figura si commenti da sola, così come si vede benissimo lo strano triangolo di Mau-Pau, con l’altrettanto "strano" teorema di Pitagora.