Quiz: Quazel contro Euclide
Ricordate la prima conoscenza con Quazel? Potete trovarla Qui, dove Quazel si cimenta con l'algebra un po' a modo suo. Dopo questa prima esperienza ne abbiamo viste altre,nel campo delle probabilità (casinò) o degli specchi da trascinare su angusti corridoi. Ma ora Quazel vuole conoscere a fondo la geometria, soprattutto quella analitica. Per far ciò si reca dal suo amico scienziato,
che comincia subito ad illustrare le caratteristiche dei sistemi di di coordinate nel piano.
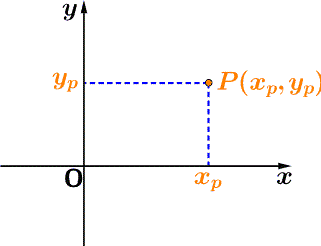
Nel nostro sistema di coordinate, dice, possiamo calcolare la distanza fra due punti con una formula molto semplice,che deriva dal teorema di Pitagora;
questa è la nostra formula della distanza ,che possiamo brevemente chiamare d(P1,P2)
Pensa possiamo descrivere un cerchio come l' insieme di punti del piano la cui distanza dal centro a sia minore o uguale a r e solo per mezzo di questa formula: d(a,P) < r.
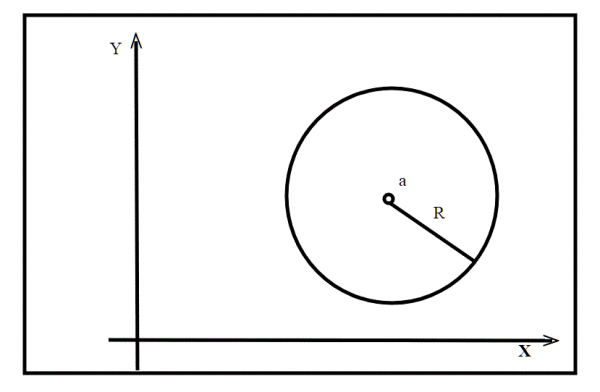
Quazel pensa e poi dice: come sarebbe a dire un cerchio? A me non risulta. Lo scienziato allora dice: ma come,ripeto che questa è la nostra formula della distanza
Lo capisce anche un bambino che applicata a d(a,P) < R delimita un cerchio. Quazel dice: Ah ho capito è la formula della distanza che e diversa dalla nostra. La nostra e questa:
dQ(P1,P2)=|x2-x1| + |y2-y1|.
(ricordo che |z| è il numero z preso sempre con il segno positivo, ed è chiamato valore assoluto di z)
Trae origine dal fatto che il nostro pianeta assomiglia molto ad un reticolo, più o meno come le vostre metropoli; per muoversi da un punto all'altro bisogna fare un percorso ad angolo retto.
E'una distanza proprio come la vostra, infatti è positiva(chiaramente se applicata a punti distinti), simmetrica (per andare da P1 a P2 si fa la stessa strada che per andare da P2 a P1). Inoltre vale sempre la diseguaglianza triangolare, come la chiamate voi:
ovvero la distanza da AC è minore della somma delle distanze AB+BC.
Lei sa disegnarmi il "nostro cerchio", ovvero il luogo dei punti del piano tali che dQ(a,P)<R e dirmi la relazione tra il vostro R e le misure della nostra figura? E la loro posizione reciproca?
Dopo aver verificato che la distanza di Quazel soddisfa la proprietà triangolare, lo scienziato riflette e poi comincia a scrivere e disegnare.
Quazel alla fine è soddisfatto.
61 commenti
volevo una conferma.... i due segmenti dell'alieno, usati per misurare la distanza, sono sempre perpendicolari tra loro?
si, fa conto che siano dei vicoli ad angolo retto in una metropoli
Capisco che quel quasi sempre riferito alla distanza di quazel può creare frantendimenti.
Era riferito al fatto che non serve fare la somma dei segmenti ortogonali qualora i due punti si trovano nello stesso vicolo o strada, ovvero basta solo un termine, dato dalla differenza non nulla fra due coordinate.
Scusate.
OK!!!
Ma... qualche differenza di coordinate può essere nulla...come nel cerchio ? O no?
si senz'altro
Perfetto! Certo è che questi alieni sono un po' difficili da trattare e si offendono spesso e volentieri. Direi che sono "spigolosi"... non trovi? Bravo Umbertino!
ho capito..mi sa che devo farli più difficili!
Ma no, dai, aspettiamo cosa dicono gli altri...
era solo una battuta..attendo con ansia i nostri risolutori
Un bel risparmio per le famiglie: invece di dover comprare costosi compassi ai figli che vanno a scuola, fanno tutto con la riga...
spero di non aver scritto un quiz troppo banale che tutti hanno già intuito: Oppure è troppo difficile?
caro Umberto,
anch'io me lo chiedo spesso... ma, penso. che rimarrà un mistero
Banale non direi proprio...
Comunque, se vogliamo aggiungere una domanda per i lettori più partecipativi, potrebbe essere questa:
Il rapporto tra circonferenza e raggio, per noi terrestri, è 2π. Quale sarà questo rapporto nella geometria descritta da Quazel?
ok può andare ma il primo passo è descrivere la figura
oppure definire la distanza come
d = |x| - |y|
La distanza è sempre definita fra due punti.
Se intendi dire di considerare il centro a del "cerchio" come (0,0) può essere un ottimo aiuto!
Sì... scusa, intendevo O come origine ....
Se ho capito bene, ponendo nell'origine degli assi il centro della figura disegnata dallo scienziato, a me viene fuori un quadrato con le diagonali parallele ai due assi. Sono arrivato a questa conclusione partendo dalla (ho considerato solo il bordo della figura , cioe' l'equivalente per Quazel della circonferenza)
/x/+/y/=R
Liberando i simboli di valore assoluto, vengono fuori 4 equazioni, rappresentative di altrettante rette che, intersecandosi , formano i 4 lati del quadrato. Il quadrato mi risulta inscritto nella circonferenza . Il rapporto tra "circonferenza" Quazeliana ed R dovtebbe essere pari a 8.
Sempre se non mi sto solo illudendo di essermi ripreso dalla crapula del mangiare e del bere dei giorni scorsi.
Grazie Arturo bella risposta anche se per ora non mi sbilancio..penso però che ci vorrebbe anche un disegnino per far comprendere bene ai lettori
le 4 rette che vengono fuori dalla relazione che definisce la "circonferenza" di Quazel sono, in forma implicita:
x+y-R=0 (per x>0 e y>0)
-x+y-R=0 (per x<0 e y>0)
-x-y-R=0 (per x<0 e y<0)
x-y-R=0 (per x>0 e y<0)
Dette rette si intersecano a due a due nei 4 punti di coordinate (R,0), (0,R), (-R,0) e (0,-R), che sono i vertici del quadrato inscritto nella circonferenza di centro O e raggio R:
Facendo variare il punto F lungo i 4 lati del quadrato, la somma /X/+/Y/ resta costante e pari ad R.
beh... direi che adesso si può anche provare a disegnare il luogo dei punti che abbiano come distanza dal centro O(0,0) la forma d =|x| - |y| (sul pianeta Angol sembra che usino questo sistema...).
Sempre che Umberto sia d'accordo, ovviamente...
e non dimenticatevi del viaggio su Alpha Centauri...
certamente se volete..manca però la diseguaglianza triangolare per entrambi le definizioni
anche se la seconda.. meglio provare con quella originale del quiz prima
Dimenticavo un Grazie ad Arturo che praticamente mi ha preparato la soluzione già scritta . MI PIACEREBBE però avere lo stesso anche una semplice opinione sul quiz, soprattutto se negativa.Per Ultimo manca la dimostrazione della disuguaglianza triangolare.
caro Umberto, a me è sembrato un bel quiz e ho aspettato a dare la risposta... ma penso che tanti ci abbiano provato con divertimento... Quanto a rispondere, sai bene come vanno le cose...
grazie so bene che avevi intuito subito.
in ogni caso il quiz non ha ancora tutte le risposte, e il significato che è molto profondo
si tratta di dimostrare che il modulo della somma x+y è minore della somma dei due moduli o la uguaglia.
il valore del modulo di x, se x è negativo è -x, se invece x è positivo il modulo vale x. quindi:
analogamente per y:
La somma di x e y è nell'intervallo:
posso riscrivere così:\leq&space;x+y\leq&space;(\left&space;|&space;x&space;\right&space;|+\left&space;|&space;y&space;\right&space;|))
ponendo: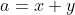
e 
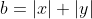posso scrivere 
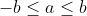quindi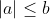 
tornando a x e y , ottengo che
Prima di mettere il becco nella geometria Enziana, vediamo se è giusto quello che ho scritto....
scusa Maurizio, ma la domanda è un po' più complessa; nella tua spiegazione abbiamo a che fare con al massimo due punti, se consideriamo l'origine; ma il triangolo deve essere formato fra tre punti del piano, non fra due coordinate di uno di essi.
Per semplificare, magari si può mettere P1 nell'origine
domani (gemelli permettendo) ci penso sopra anch'io...
benissimo
ho ancor un attimo di tempo...
temo di non aver capito bene cosa si deve dimostrare... I triangoli restano triangoli... o sbaglio? Al limite, potrei dire che sono esclusi dal "cerchio" i lati lungo x e y, dato che per loro la somma di due lati è uguale al terzo lato (triangoli degeneri)... Potresti spiegarmi meglio la faccenda? Non vorrei che qualche lato si ... contraesse relativisticamente!
P.S.: la distanza è definita in modo diverso, ma dovrebbe comunque valere Pitagora... o no?
Una domanda "sbarazzina"...Se assumo il punto P1 come origine e traccio i vettori P1P2 e P1P3 posso affermare che il vettore differenza è P3P2. Tra questi vettori sussiste la disuguaglianza triangolare. Non è lecito dire che anche tra le componenti di questi vettori ( proiezioni sull'asse x e sull'asse y) sussiste la medesima proprietà?
quello che bisogna dimostrare e quello che di vede dal disegno:no non vale Pitagora
Ah.... ho capito adesso. P1P2 è sempre la somma di due segmenti perpendicolari tra loro
...hai ragione!
esattamente!
a dir la verità il titolo avrebbe dovuto essere Quazel contro Pitagora!
Fermi tutti! Forse è qualcosa del genere (sono con un piede fuori da casa....). Il terzo lato deve sempre essere formato da segmenti che sono la differenza tra gli altri segmenti dei rimanenti lati e quindi la somma dei due segmenti è sempre minore della somma degli altri quattro.... o qualcosa del genere. Domani lo scrivo per bene con qualche disegnino....
mu aspetto una soluzione geometrica perché se procediamo algebricamente..ê un casino
detto a parole....
La somma di due lati è data dalla somma dei loro segmenti componenti (2 verticali e 2 orizzontali).
il terzo lato ha come componenti il modulo della differenza delle relative componenti degli altri due lati.
La somma delle due differenze è comunque minore della somma delle due somme.
vedo belle idee..bisognerà spiegarle bene
Direi così...
lato P1P2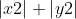
lato P1P3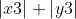
loro somma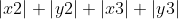
= 
lato P2P3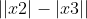
+ 
<= 
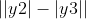Devo dimostrare che
AC < AB + BC (1)
Suppongo che non sia vera la (1) cioe' che
AC > AB+BC (2)
Per Quazel:
AC = AF + FC
AB = AD + DB
BC = BE + EC
Sostituendo nella (2):
AF+FC>AD+DB+BE+EC (3)
Ma dalla figura si vede che DB+BE=AF e che FC+EC =AD quindi dalla (3):
FC>AD+EC --> FC>FC+2EC-->EC<0
il che e' impossibile. Quindi la (1) deve essere vera.
(la figura e il testo li ho scritti col cellulare prima di poggiarlo sul comodino..
)
Sto andando a spizzichi... per adesso posso dire che il triangolo per l'alieno diventa un rettangolo, come questo
adesso basta dimostrare che la parte verde o rossa o nera è minore della somma delle altre due... Appena posso ci torno sopra...
sembra che Arturo abbia ancora colpito nel segno.. del resto è il nostro esperto in Geometria. Si ,nella diseguaglianza parlando di distanze in genere si mette il minore uguale, anche se per la distanza pitagorica non vale mai l'uguale. Mi disturbano un po'le ipotenuse che fanno pensare che la distanza sia ancora la congiungente i due punti(Pitagora) ma se sono necessarie per la comprensione della dimostrazione lasciamole pure lì.
Chi vuole divertirsi trovi la forma del cerchio con questa altra distanza:
d(P1,P2)=max{|x2-x1|+|y2-y1|}
Direi che il mio rettangolo sia in perfetto accordo con quello di Arturo. Il perimetro del triangolo alieno è il perimetro del rettangolo. La somma di due lati è sempre maggiore della metà del perimetro del rettangolo, tranne nel caso in cui il triangolo sia rettangolo (due lati degenerano in un solo segmento).
Umberto non mi ha risposto, ma penso di essere nel giusto...
aspettavo che finissi.quando esco da questo maledetto ambulatorio lo leggo più a fondo
fai le cose con calma... spero che non sia niente di importante...
ricette.. Noi a Belluno siamo indietro con l elettronica
Scusa Vincenzo ma non vedo...tu parli di somma di due lati ma non capisco quali siano. Quelli del rettangolo? Se per favore puoi mettere delle lettere ed esplicitare le somme forse riesco a capire meglio
Lo sfondo scuro e tra virgolette dell'ultimo periodo della mia precedente risposta non erano voluti. Devo aver pigiato inavvertitamente qualche pulsante nella finestra di inserimento testo.
Sorry.
Mentre attendiamo gli ultimi risvolti, ripropongo:
Chi vuole divertirsi trovi la forma del cerchio con quest' altra distanza:
d(P1,P2)=max{|x2-x1|,|y2-y1|}
è un po' piu semplice
Mi limito al primo quadrante, ma le cose non cambiano passando agli altri...
Il perimetro del triangolo OAB alieno è dato dal rettangolo di figura. La somma di due lati (ad esempio OA e OB) è per costruzione maggiore del lato AB, dato che coprono più di metà del perimetro. Identica situazione si avrebbe cambiando i lati... Se A B fossero sugli assi y e x (caso degenere) avremmo che la loro somma sarebbe uguale al terzo lato.
La relazione decisiva è che la somma di due lati è sempre maggiore della metà del perimetro del rettangolo (triangolo alieno) e quindi è sempre maggiore del terzo lato.
Va beh... torno ai miei gemellini Muo1 e Muo2
Forse adesso ho capito; mi confondevo quando parlavi di OA e OB, tu per OA intendo OA'+ A'A. Si.(ma poi lo sapevi da solo)
bene non vorrei essere insistente, ma per presentare la mia introduzione agli spazi metrici e topologici sarebbe bello disegnare il cerchio corrispondente alla distanza:
d(P1,P2) , massimo(I x2-x2 I, I y2-y1 I)
é molto più semplice e divertente.Poi mi arrendo.
La distanza è definita come il valore massimo tra la componente orizzontale e la componente verticale
Fisso il raggio = modulo (x2-x1) e il centro (x1,y1)
il "cerchio" è il quadrato circoscritto al cerchio (euclideo) di raggio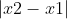
e centro x1,y1.
Immagino il raggio che esce dal centro x1,y1 e interseca il "cerchio" quadrato, e lo osservo ruotare: finché non arriva ai 45° la distanza è la proiezione orizzontale, sulle x, maggiore della proiezione verticale, sulle y. In corrispondenza ai 45° le due proiezioni sono uguali, oltre ai 45° la situazione si inverte e la componente verticale è quella massima, fino a 135° , e così via fino a completare il giro.
Quindi era corretta l'ultima versione della nuova definizione, cioè
d(P1,P2) = massimo(|x2-x2|, |y2-y1|)
Prima al posto della virgola c'era un + e non riuscivo a trovarne il senso.
E' curioso notare che anche in questo caso il rapporto tra la misura della "circonferenza" Quazeliana nuova versione e il raggio mi pare sia uguale a 8.
Si Maurizio, è proprio un quadrato circoscritto al cerchio Euclideo.
Non c'erano due versioni, era solo un errore di scrittura, che ho corretto . La distanza è proprio questa:
d(P1,P2) = massimo(|x2-x2|, |y2-y1|)
Il fatto è che non dovrei scrivere queste cose con il cellulare, considerando anche la vista pessima che ho.
Bene, sono molto soddisfatto e scriverò al più presto la soluzione, che altro non sarà che un merge di quello che avete scritto voi
che figura disegna lo scienziato? un quadrato inclinato di 45° rispetto a come si disegna normalmente. qualcuno potrebbe dire che si tratta di un rombo con i lati uguali.
Che misure ha rispetto al cerchio? la diagonale del quadrato è pari al diametro del cerchio
Qual è la loro posizione reciproca rispetto al punto a? sono concentrici
E' inoltre vero che la distanza di Quazel rispetta la disuguaglianza triangolare? sì
Ciao Shedir!
Noto con piacere che sei intervenuto spesso (e con competenza!) nella soluzione degli ultimi quiz presentati in questo Circolo (lo so, può sembrare strano chiamarlo in questo modo antiquato, ma che ci vuoi fare... siamo un po' strani, te ne sarai accorto
).
Se vuoi continuare a divertirti con i quiz, puoi attingere all'intero archivio QUI: ne troverai per tutti i gusti! Non preoccuparti se, nel frattempo, sono stati risolti, non devi fare altro che scrivere la tua soluzione senza leggere i commenti precedenti (oppure li puoi anche leggere, che male c'è? In tal caso basta dirlo...).
E se risolverai un quiz del prof., che ancora per qualche tempo non potrà risponderti, ci sarà senz'altro uno dei validissimi collaboratori a farlo per lui.
Buon divertimento!!