Categorie: Relatività
Tags: calcolo terrestre a posteriori... inversione rotta iperbole di calibrazione paradosso dei gemelli
Scritto da: Vincenzo Zappalà
Commenti:15
Gemelli iperbolici… ***
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
In attesa delle favole sui gemelli, vi propongo un ulteriore modo (rispetto a quelli che abbiamo spiegato QUI) per arrivare subito a risolvere il paradosso dei gemelli che spero sia ancora più intuitivo. La RR non cambia di certo, ma viene sfruttata solamente l’iperbole di calibrazione (QUI fig. 31 e seguenti). Fatemi sapere se siete d’accordo oppure no…
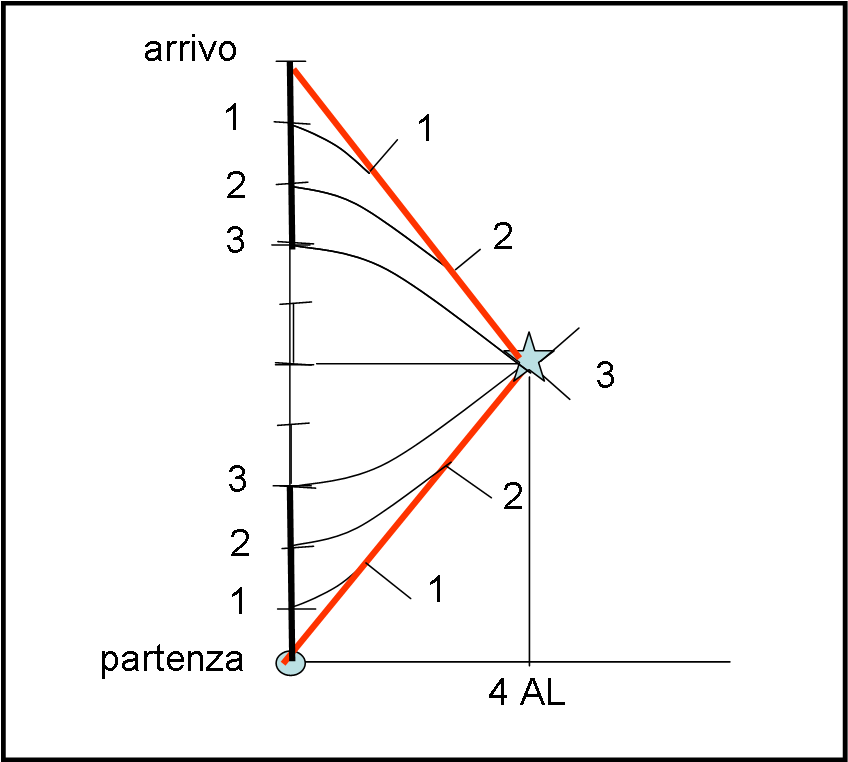
La situazione è sempre la stessa, illustrata nella figura che segue
La linea verticale del tempo è quella relativa al tempo che trascorre per un orologio che è solidale con la Terra. A noi interessano due eventi che hanno la stessa posizione spaziale (Terra), ma tempi diversi. Esso sono la partenza e l’arrivo dell’astronave che raggiunge Alpha Centauri. Lo calcoleremo a posteriori.
Disegniamo le iperboli di calibrazione per ogni unità di tempo annuo terrestre 1, 2, 3,…. Esse ci permettono di stabilire immediatamente il corrispondente tempo annuo unitario relativo all’astronave che va verso Alpha Centauri con v = 0.8c.
Vediamo che all’arrivo su Alpha sono passati 3 anni sulla rotta dell’astronave (sistema in moto).
Ciò vuol dire che invertendo la rotta deve capitare la stessa cosa rispetto all’evento arrivo dell’astronave sulla Terra. Partendo dalla posizione dell’astronave all’anno 3 (in Alpha), basta invertire il sistema di iperboli e si otterrà l’evento “arrivo” sulla linea temporale della Terra.
Per costruzione il numero di anni passati sull’astronave sono 3 + 3 = 6 anni. Quanti sono quelli passati sulla Terra? Molti di più… basta segnare gli anni terrestri fino a incontrare l’evento arrivo astronave sulla Terra. Il calcolo è presto fatto: sono passati 10 anni.
Viaggiando sull’astronave e invertendo la rotta si sono saltati 4 anni terrestri.
Che ne dite?
QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli






15 commenti
Ma… io non sono tanto d’accordo, ma ovviamente è solo la mia opinione personale.
Forse non ho ben capito cosa vuoi dire…
Secondo me usare l’iperbole di calibrazione non è un buon metodo, anche se sembra che i conti alla fine tornino, perché non include la retta di simultaneità.
In particolare la tua frase:
“Viaggiando sull’astronave e invertendo la rotta si sono saltati 4 anni terrestri”
non è molto corretta, anche se 10 meno 6 fa proprio 4.
Allora dal punto di vista del terrestre, non si salta nessun tempo, ma per 10 anni da lui trascorsi, dal suo punto di vista, ne passano 6 per l’astronauta (dilatazione dei tempi).
Dal punto di vista dell’astronauta, ovvero viaggiando sull’astronave e invertendo la rotta non vengono saltati 4 anni terrestri, ma molti di più (ribadisco dal punto di vista dell’astronauta).
Perché bisogna tracciare la retta di simultaneità, e trovare i corrispettivi valori sull’asse dei tempi del terrestre, che non sono quelli ottenuti con l’iperbole.
Ovvero nei 6 anni che passano per l’astronauta, dal suo punto di vista, non ne passano 6 per il terrestre ma 3.6, perché bisogna mantenere la simmetria (dilatazione dei tempi).
Quindi il salto è molto di più di 4 anni, in particolare è di 6.4 anni.
Ma forse ho frainteso quello che volevi dire, o forse sono troppo puntiglioso io.
caro Simone,
la tua trattazione è sicuramente più corretta formalmente ed è anche una di quelle che è stata usata precedentemente. Tuttavia, il mio scopo era di rendere più immediata la visione del salto temporale. Al di là della simultaneità, la curva di calibrazione ci pone di fronte alle unità dei vari sistemi e sono proprio quelle che vanno confrontate. Non ci vedo niente di veramente "scorretto" da un punto di vista interpretativo, In fondo esse nascono proprio attraverso le basi della RR e della relatività della simultaneità...
Insomma, non prendiamola come troppo tecnica, ma come un sistema rapido per vedere la differenza in modo immediato...
Caro Simone,
in altre parole, dove sarebbe l'eventuale errore, visto che agendo in questo modo spuntano proprio i 4 anni di differenza? Ho solo sfruttato il concetto di iperbole di calibrazione... tuttavia, essendo un manovra un po' anomala, ben vengano le correzioni.... e ti ringrazio
cari ragazzi,
prendete esempio da Simone e cercate di contestare la versione facilitata. Ovviamente, ci vogliono prove chiare di dove sia l'errore. Forse non ci crederete, ma sarei veramente contento perché ciò dimostrerebbe il livello raggiunto e la capacità di chi partecipa. Collaborazione e umiltà. Sarei il primo ad essere soddisfatto di quanto raggiunto e ritratterei l'esposizione... A questi livelli di comprensione un dibattito è più che auspicabile. Questa è la vera differenza da un forum dove si può dire di tutto senza avere le basi. Un doppio grazie a Simone e spero che non sia l'unico...
Caro Simone...
il metodo che esponi tu si basa sulla simultaneità diversa dei tre sistemi di riferimento e a me piace molto, pur essendo più tecnico. Lo hai riportato nei commenti al quiz, ma varrebbe la pena fare proprio tutti i calcoli nei tre sistemi e un paio di figure che indichino bene le coordinate degli eventi visti nei tre sistemi. Se vuoi puoi cercare di espanderlo in modo da renderlo più comprensibile ai lettori (se preferisci, però posso faro anch'io... come preferisci).
Utilizzare l'iperbole l'ho visto come un modo di sveltire il tutto: la costruzione dell'iperbole segue proprio dal concetto di diversa simultaneità, ma non ha bisogno di riferirsi ai singoli sistemi... Il tutto è già compresso nei luoghi che danno la stessa unità, ossia proprio il tempo proprio a varie velocità...
Vista la tua preparazione, gradirei molto sia la scrittura dell'articolo più esteso, cercando però di partire proprio dalle trasformazioni di Lorentz e applicarle ai tre sistemi per trovare le coordinate e, di conseguenza gli intervalli di tempo e la loro somma sia una critica basata su dati di fatto del tentativo... iperbolico.
In qualche modo aiuteremmo il Circolo a comprendere una volta per tutte il paradosso spiegato senza effetto doppler (che proprio mi piace poco, anche se l'avevo usato anch'io nell'approfondimento ed è stato esposto da Umberto). Poi metteremo tutto assieme in un approfondimento dedicato... (ci sta anche lavorando Paolo...).
Infine, sta per uscire una triplice versione ironica basata su una barzelletta che vede le grinfie di Maurizio, PapalScherzone e in parte anche la mia.
Insomma, il paradosso dobbiamo proprio stritolarlo come nessuno ha mai fatto (forse...).
Fammi sapere e... attendo anche altre opinioni
a me quei calcoli sostanzialmente vanno bene, altro non sono che quelli del quiz sul tempo proprio con l invariante , applicato due volte. I miei problemi sono altri, e non centrano con le tue spiegazioni. Quel triangolo che rappresenta l inversione istantanea Dell astronave per me non ha alcun significato fisico, nemmeno a livello di esperimento mentale. Ripeto: É l esposizione del paradosso cosi com'è stato concepito che non digerisco .certi usano l escamotage delle due astronavi che si incrociano e il gemello che salta da una all altra, ma poco cambia. per me bisognerebbe costruire una curva reale con accelerazione iniziale, fermata decelerata, accelerazione e poi l altra fermata decelerata.Cosi potremmo integrare Tau su tale curva e dimostrare il paradosso.Però la matematica necessaria non è accessibile a tutti .
Una domanda molto naif... Se i due gemelli partissero su due astronavi che vanno di pari passo, alla stessa velocità, compissero le medesime manovre di accelerazione e decelerazione e alla fine tornassero sulla Terra, avrebbero di certo la medesima età. E se invece di viaggiare per lo stesso tempo, pur compiendo manovre identiche dal punto di vista della dinamica, uno si spingesse più lontano dell'altro, non sarebbe immediato dire che la differenza di età è calcolabile in base alla sola differenza del percorso ( a velocità costante) compiuto?
senza far calcoli di lunghezze (Minskoniane) di curve é difficile rispondere.l importante è che il segmento è la curva più lunga fra due punti.e corrisponde al gemello fermo.
Grazie per le risposte.
Io ho sollevato la critica al metodo dell’iperbole di calibrazione, non tanto per il fatto che sia più o meno giusto concettualmente.
Io penso che come sistema per semplificare possa essere anche corretto.
Quello che mi fa storcere il naso, è il fatto che dal tuo diagramma sembra che passino 6 anni per l’astronauta, ai quali corrispondono 6 anni per il terrestre più un salto di 4 anni.
Io dico che il salto è 6.4 anni, se non ho sbagliato i calcoli, e non 4.
Quindi andrebbe detto:
Viaggiando sull’astronave e invertendo la rotta si sono saltati 6.4 anni terrestri.
Cioè quello che voglio dire è che il salto o è 4 anni o è 6.4, non possono valere entrambe le affermazioni.
Ovviamente va spiegato il perché.
Io mi sono basato sul diagramma di Minkowski, usando la retta di simultaneità, e calcolando i vari tempi dei vari eventi.
Ripeto, il tuo sistema può essere anche corretto, soprattutto in una ottica di semplificazione, resta il fatto che a me personalmente mi lascia perplesso il valore numerico del salto.
Se un lettore legge pensa che nell’inversione siano stati saltati 4 anni, e invece sono 6.4.
Ti ringrazio anche per la fiducia che mi hai concesso, ma per scrivere un articolo più esteso avrei bisogno di più tempo, che purtroppo non ho.
Magari con più calma più avanti, adesso vedo.
Comunque piacerebbe anche a me un articoletto ben strutturato dove si calcolino tutti gli eventi, visti sia dal terrestre che dall’astronauta.
Io ho usato il diagramma di Minkowski, ma sarebbe molto bello usare anche la trasformata di Lorentz, in modo da convalidare una volta per tutte il diagramma stesso.
Sarebbe scacco matto al paradosso dei gemelli, una volta per tutte.
Volevo fare una ulteriore osservazione.
Noi abbiamo parlato di salto temporale, cosa che potrebbe impressionare, e porre ulteriori interrogativi.
In realtà, come tu ben sai, questo è vero solo se l’inversione fosse istantanea.
Nella realtà non lo può essere, ovvero andrebbe considerata la fase di decelerazione e la successiva accelerazione, per tornare indietro.
Nel diagramma di Minkowski, questo si traduce in una curva.
In pratica è come se ci fosse un continuo cambiamento di sistema di riferimento, con un continuo cambiamento della retta di simultaneità.
L’astronauta vedrebbe l’orologio del terrestre, sia nella fase di decelerazione, che accelerazione, girare più velocemente del proprio.
Ma questo è concorde con la RG, che dice che in un sistema accelerato, l’orologio più in alto (in questo caso il terrestre) deve girare più velocemente del proprio.
Nota che vale sia per la fase di decelerazione, che la successiva fase di accelerazione, ovvero le due fasi non si annullano a vicenda, perché se ci pensi la forza che subisce l’astronauta è sempre nello stesso verso, ovvero cerca di allontanarlo dalla terra.
Alla partenza e all’arrivo, andrebbero comunque considerate le due accelerazioni, ma l’effetto è ben minore, perché la terra è molto meno in alto rispetto all’astronauta.
Comunque è un discorso in stato embrionale, non tutto mi è chiaro, ma sto facendo un passo alla volta…
Ci sto pensando su con calma, ma sarebbe bello che un giorno anche tu lo trattassi con un articolo ben fatto, magari parlando anche dei moti iperbolici.
Cercare di calcolare esattamente accelerazioni e decelerazioni mi sembra una fatica del tutto inutile. In fondo, basta dire che il triangolo basato sull'invariante è valido anche se si smussano gli angoli e quindi anche con accelerazioni e decelerazioni. Si tratta "solo" di far variare continuamente Minkowski lungo la tangente alla curva. Tuttavia, il vero interesse, per me, è verificarlo con solo la RR. E per far questo direi che l'idea di un altro astronauta gemello che arrivi su Alpha nel momento del secondo e continui tranquillo verso la Terra è la miglior approssimazione.
Per Simone.
NON capisco perché non ti piace lo scatto dei 4 anni... Il risultato finale è proprio 10 a 6...
Caro Enzo, come sai sto lavorando ad un racconto in cui utilizzerò le line di simultaneità dell’astronave all’andata ed al ritorno (cambio di sistema di riferimento).. sto anche costruendo alcune figure ed animazioni.
A me il metodo veloce delle iperbole di calibrazione non dispiace.
Capisco cosa intende Simone, sul salto temporale e vorrei provare a dire la mia in proposito.
Con le curve di calibrazioni il valore di 4 anni indica la differenza complessiva tra i due tempi (propri) trascorsi: quello del gemello terrestre (10 anni) e quello del gemello astronauta (6 anni).
Il valore di 6,4 anni, invece indica il salto temporale che avviene durante l’inversione di rotta.
La differenza tra questi due valori è dovuta al fatto che anche l’astronave vede gli intervalli di tempo della Terra dilatarsi.
Pertanto:
all’andata, quando l’astronave ha percorso 3 anni, per il sistema di riferimento del gemello astronauta sulla Terra sono passati 1,8 anni;
al ritorno restano da percorrere 3 anni per rientrare a Terra, perciò per il sistema di riferimento dell’astronauta, sulla Terra ne devono passare 1,8.
Pertanto 10 anni – (1,8 x 2) = 10 -3,6 = 6,4 anni.
Il salto temporale avviene durante l’inversione di rotta.
Inversione che costringe l’astronave a cambiare sistema di riferimento… passando da velocità +0,8c a velocità 0 e poi a velocità -0,8 c. Tale passaggio si presume avvenga in un tempo rapidissimo giusto per non dover fare i conti con accelerazioni e decelerazioni e rimanere nella RR… comunque per rimanere in ambito RR si potrebbe pensare all’inversione di rotta come un continuo mutamento del sistema di riferimento, con relativa continua modifica degli assi t’ e x’, fino alla totale inversione di marcia.
Spero di non aver detto qualche sciocchezza.
Paolo
cari amici,
state dicendo cose verissime, ma sono valide entrambe le cose a seconda di come si vuole vedere il problema. Il salto di Simone è un salto basato sulla simultaneità, ma che alla fine porta a una somma totale dei tempi corretta lavorando con le coordinate dei vari sistemi. Io ho solo cercato di semplificare confrontando unità con unità. In tale contesto, la differenza rimane comunque una differenza di tempi propri. Ricordiamo che l'iperbole permette di confrontare direttamente tempi propri, mentre la simultaneità permette di valutare le dilatazioni viste da entrambi i sistemi.
Sto cercando di far vedere bene come le simultaneità e le relative dilatazioni si uniscano bene alle iperboli. Successivamente considererò i TRE sistemi di riferimento necessario e le coordinate degli eventi interessanti nei tre sistemi. Voglio dimostrare che per tutti e tre i sistemi il tempo passato sulla terra è 10 anni, contro i 6 che misurano con i propri orologi (v o - v conta poco) i viaggiatori. La somma dei vari intervalli dà sempre lo stesso risultato e le differenze sono da imputare alle trasformazioni di Lorentz usate direttamente.e non all'unificazione fatta da Minkowski con l'iperbole di calibrazione.
Per Umberto. Ciò che puoi veramente fare con l'integrazione è considerare una curva tra la partenza l'arrivo su alpha e il ritorno. La curva è sicuramente più corta, ma potresti controllare quanto sia più corta integrando sulla curva, tenendo conto che la variazione degli assi avviene in modo continuo (accelerazione costante).
Integrare basandosi sulle formule della relatività generale è fuori da qualsiasi nostra idea divulgatrice. inoltre, noi siamo interessati ai tempi diversi tra chi viaggia e chi no e possiamo benissimo considerare trascurabili i tempi di accelerazione e decelerazione senza incorrere in errori significativi.
Da quanto ho capito, Paolo ed io troveremo qualcosa di molto simile che dovrebbe soddisfare anche Simone. Resto, comunque dell'idea, che la differenza di tempo ottenuta con le iperboli sia reale, considerando tempi propri...
Chi non è interessato a questo paradosso, abbia pazienza... e si diverta con la versione favolistica che uscirà tra poco (senza arrabbiarsi se la chiesa ne uscirà un po' male... ma ci ha abituato a farlo...).
Basta non dico altro!!!! Buon lavoro a tutti. Questo circolo sta diventando una vera "officina" e le stelle malate devono ancora aspettare....
No no lasciamo stare la relatività generale che non conosco nemmeno. Ti dirò in seguito qual era la mia idea. Ho cercato invece di capire la differenza di calcoli fra tu e Simone; nel calcolo dell invariante che hai fatto se nel sistema in moto t è 3 la distanza non e quattro ma 2,4 : per il gemello in moto il tempo a terra verrebbe 1,8 e di conseguenza per due 3,6 che sottratto a 10 da proprio 6,4. Per me è solo un errore di calcolo.
No, Umberto... una cosa è calcolare la dilatazione del tempo su un sistema in movimento e un'altra è descrivere l'iperbole. Ti consiglio vivamente di guardare le fig. 33 e 34 dell'approfondimento su Minkowski. Lì la differenza è immediata. Comunque nella trattazione che sto scrivendo ci torno sopra...
Ok, mi dispiace. Speravo di aver scoperto l'inghippo.