Categorie: Fisica di Papalla Relatività
Tags: paradosso dei gemelli
Scritto da: I Papallicoli
Commenti:20
I due gemelli diversi
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
Nonostante le gigantesche limitazioni, gli ominidi del terzo pianeta del sistema solare, in qualche modo erano riusciti a costruire astronavi in grado di viaggiare a velocità prossime a quelle della luce salvaguardando i fragili organismi viventi al loro interno.
La vicina stella Alpha Centauri distava solo 4 anni luce ed i terricoli avevano costruito quattro stazioni spaziali distanziate fra loro di 1 anno luce, l’ultima delle quali in orbita intorno ad Alpherra, il terzo pianeta della stella Alpha Centauri.
La stazione Alpha 1 distava un anno luce dalla Terra, Alpha 2 due anni luce, Alpha 3 tre anni luce e Alpha 4 quattro anni luce.
I terricoli sapevano molto bene che la distanza tra la Terra e le 4 stazioni spaziali era sempre la stessa, pertanto queste appartenevano tutte allo stesso sistema di riferimento.
Inoltre, qualunque segnale proveniente da Alpha 1, viaggiando alla velocità della luce, avrebbe impiegato esattamente 1 anno per raggiungere la Terra, così come qualunque segnale proveniente da Alpha 2 avrebbe impiegato 2 anni per raggiungere la Terra e così via.
Sulla Terra ancora tutti ricordavano quando era arrivata la notizia che su Alpha 1 era scoppiato un incendio. Nessuno sulla Terra poteva far nulla per aiutarli, poiché quell’incendio era accaduto un anno prima, visto che la notizia aveva impiegato esattamente 1 anno per arrivare fino a Terra.
I grandi orologi presenti nelle 4 stazioni spaziali erano stati tutti sincronizzati con quello terrestre, proprio tenendo conto del tempo necessario alla luce (onde radio comprese) per percorrere la distanza che separava le stazioni spaziali dalla Terra.
Pertanto quando su Alpha 1 era scoppiato l’incendio, l’orologio della stazione indicava che erano le 14:00 del 13 gennaio 2098, mentre la notizia dell’incendio era arrivata sulla Terra esattamente alle 14:00 del 13 gennaio 2099.
Sulla Terra alle 14:00 del 13 gennaio 2098, mentre su Alpha 1 scoppiava l’incendio, era in corso il torneo di lanci lunari, su Alpha 2 l’equipaggio giocava ad Astropoker (ma sulla Terra lo avrebbero saputo 2 anni dopo), su Alpha 3 festeggiavano il compleanno di Angelo del deserto (ma sulla Terra lo avrebbero saputo 3 anni dopo), su Alpha 4 si divertivano a contare le orbite compiute intorno ad Alpherra (ma sulla Terra lo avrebbero saputo 4 anni dopo).
Nella Figura sottostante, viene rappresentato il ritardo con cui l’informazione proveniente dalle stazioni spaziali, che viaggia alla velocità della luce, giunge sulla Terra.
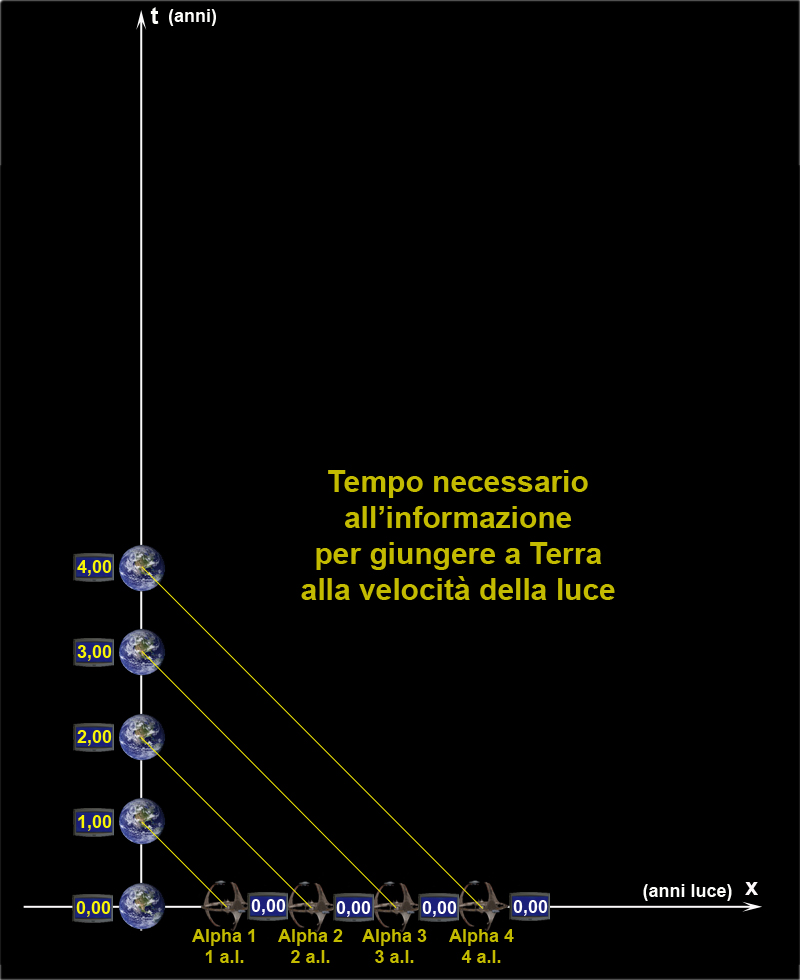
Il 1 gennaio del 2100 era previsto il lancio di un’astronave per un viaggio di andata e ritorno verso Alpha Centauri.
Sull’astronave sarebbe salito il Sig. Flash, gemello del Sig. Stop, che al contrario del fratello non aveva alcuna intenzione di avventurarsi nello spazio.
L’astronave era in grado di raggiungere in un tempo brevissimo una velocità costante di crociera pari all’80% della velocità della luce (V = 0,8 c).
Per il gemello rimasto a Terra, abituato a ragionare solo secondo il suo sistema di riferimento, tutto sembrava scontato.
All’andata Flash avrebbe raggiunto la stazione Alpha 1 dopo 1,25 anni (T = S/V = 1/0,8 = 1,25), Alpha 2 dopo 2,5 anni (T = 2/0,8 = 2,5), Alpha 3 dopo 3,75 anni (T = 3/0,8 = 3,75), Alpha 4 dopo 5 anni (T = 4/0,8= 5).
Come previsto, la stazione Alpha 1 aveva segnalato l’arrivo dell’astronave dopo 1,25 anni dalla partenza ed ovviamente tale segnalazione era arrivata sulla Terra 1 anno dopo, ossia dopo 2,25 anni dalla partenza (Tempo arrivo informazione T + 1 anno = 1,25 + 1), Alpha 2 aveva segnalato il passaggio dopo 2,5 anni dalla partenza e la segnalazione era giunta a Terra dopo altri 2 anni (2,5 + 2 = 4,5 anni dalla partenza), Alpha 3 aveva segnalato il passaggio dopo 3,75 anni dalla partenza e la segnalazione era giunta a Terra dopo altri 3 anni (3,75 + 3 = 6,75 anni dalla partenza), Alpha 4 aveva segnalato il passaggio dopo 5 anni dalla partenza e la segnalazione era giunta a Terra dopo altri 4 anni (5 + 4 = 9 anni dalla partenza).
Il gemello rimasto a Terra era perfettamente soddisfatto. Tutto sembrava svolgersi proprio come si aspettava.
Durante il viaggio di ritorno Flash aveva raggiunto la stazione Alpha 3 dopo 1,25 anni da Alpha Centauri, o meglio dopo 6,25 anni dalla partenza (5 + 1,25) e tale segnalazione per giungere fino alla Terra aveva impiegato altri 3 anni (6,25 + 3 = 9,25 anni), dopo 7,5 anni dalla partenza (5 + 2,5) aveva raggiunto Alpha 2 e la segnalazione aveva impiegato altri 2 anni per arrivare a Terra (7,5 +2 = 9,5 anni), dopo 8,75 anni aveva raggiunto Alpha 1 (5 +3,75) e la segnalazione aveva impiegato un altro anno per giungere a Terra (8,75 +1 = 9,75 anni) ed infine dopo 10 anni dalla partenza (5 +5 = 10) Flash era tornato sulla Terra.
Il gemello rimasto a Terra ha disegnato anche una figura per mostrare il viaggio di andata e ritorno dell’astronave, così come lui lo ha immaginato.
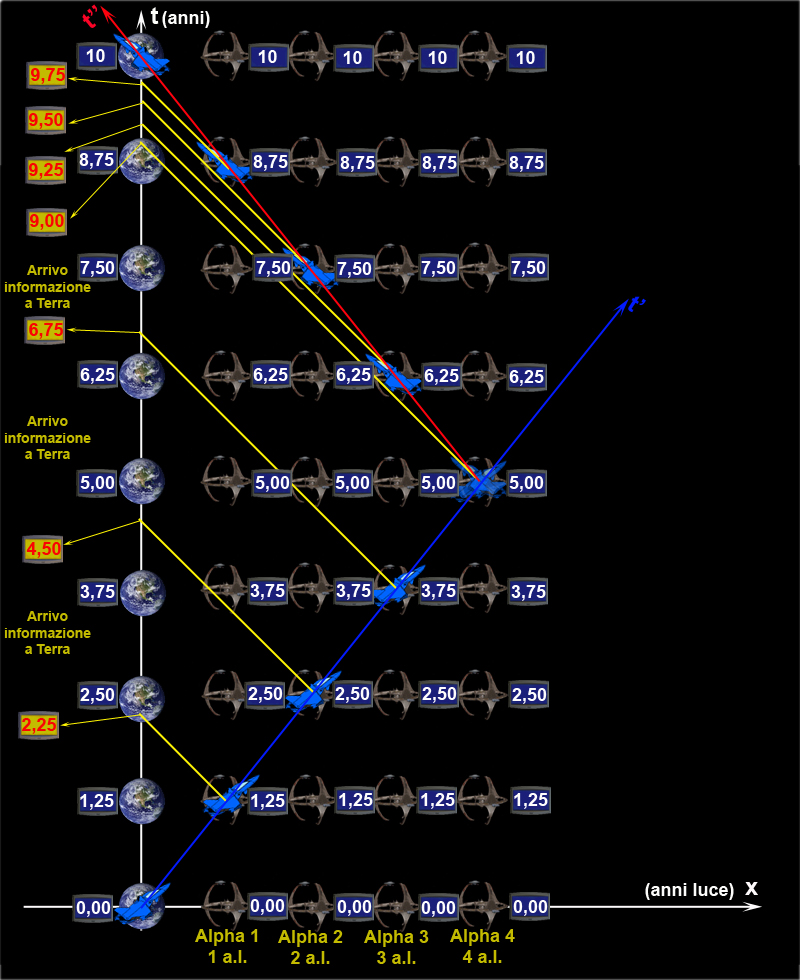
Il Sig. Stop continua ad essere convinto che tutto sia andato esattamente come previsto, finché Flash non scende dall’astronave.
Accidenti esclama Stop, caro fratello il viaggio spaziale sembra aver frenato il tuo invecchiamento e sembri decisamente più giovane di me.
Cosa hai mangiato per tenerti così in forma?
Flash, invece, non può far altro che esclamare: ma cosa ti è successo? Sono passati solo 6 anni, ma sembri invecchiato di 10!
Come sono passati solo 6 anni? Ne sono passati 10 e non 6, come indica chiaramente il mio orologio terrestre!
No, ne sono passati solo 6, replica Flash, come indica chiaramente l’orologio della mia astronave.
Ma scusa dice Stop, come può essere che tu abbia percorso 10 anni luce (5 all’andata e 5 al ritorno) in soli 6 anni?
Hai forse viaggiato più veloce della luce?
Flash ci pensa un po’ prima di rispondere a Stop.
Guarda il diario di bordo dell’astronave ed esclama: ah dimenticavo, secondo gli strumenti di Bordo il percorso era di 2,4 anni luce all’andata e 2,4 anni luce al ritorno.
Stop che fino ad allora riteneva il suo sistema di riferimento perfetto e infallibile, non sa più cosa pensare.
Caro fratello esclama Stop è del tutto evidente che la strumentazione dell’astronave è difettosa.
Ti sbagli di grosso, risponde Flash, gli strumenti funzionano benissimo… e poi come spieghi che io sono più giovane di te?
A questo punto i due gemelli decidono di chiedere aiuto ad Albert, che segue i viaggi delle astronavi dalla torre di controllo.
Albert, rassicura i due gemelli che gli strumenti funzionano perfettamente e che quando si trovano nello stesso sistema di riferimento le misure delle distanze spaziali e del tempo funzionano benissimo, altrimenti…
Altrimenti cosa, rispondono perplessi i due gemelli?
Per rispondere, Albert invita Flash e Stop ad analizzare con calma il viaggio di andata e ritorno, osservando i dati in possesso della torre di controllo.
Quando l’astronave è passata dalla stazione spaziale Alpha 1, l’orologio della stazione, sincronizzato con quello della Terra, segnava che erano passati 1,25 anni dalla partenza (tempo improprio), ma dalla stazione spaziale si vedeva chiaramente che l’unico orologio dell’astronave (tempo proprio) indicava che erano passati solo 0,75 anni.
Albert mostra ai due gemelli una tabella con indicato cosa segnavano gli orologi delle stazioni spaziali sincronizzati con quello terrestre e cosa indicava l’unico orologio dell’astronave visto dalle stazioni spaziali:
|
Stazione Spaziale |
Orologi sincronizzati con la Terra |
Orologio dell’astronave |
|
Alpha 1 (Andata) |
1,25 anni dalla partenza |
0,75 anni dalla partenza |
|
Alpha 2 (Andata) |
2,5 anni dalla partenza |
1,5 anni dalla partenza |
|
Alpha 3 (Andata) |
3,75 anni dalla partenza |
2,25 anni dalla partenza |
|
Alpha 4 (Andata) |
5 anni dalla partenza |
3 anni dalla partenza |
|
Alpha 3 (Ritorno) |
6,25 anni dalla partenza |
3,75 anni dalla partenza |
|
Alpha 2 (Ritorno) |
7,5 anni dalla partenza |
4,5 anni dalla partenza |
|
Alpha 1 (Ritorno) |
8,75 anni dalla partenza |
5,25 anni dalla partenza |
|
Terra 4 (Ritorno) |
10 anni dalla partenza |
6 anni dalla partenza |
Ma come è possibile esclama STOP, il tempo è il tempo per chiunque e l’astronave non può viaggiare più veloce della luce!
Ti sbagli di grosso risponde Albert, il tempo, così come la misura delle distanze non è uguale per tutti, non è assoluto, ma relativo e dipende dal sistema di riferimento.
L’astronave di Flash per la Terra si muove e la sua distanza dal pianeta e dalle stazioni spaziali varia continuamente, per cui non appartiene al sistema di riferimento terrestre.
E come la mettiamo con le distanze percorse, chiede STOP?
Albert, non si scompone minimamente e presenta un'altra tabella che mostra anche la diversa misura delle distanze:
|
Stazione Spaziale |
Distanza dalla Terra misurata dal suo sistema di riferimento |
Distanza misurata dall’astronave appena ha raggiunto alla partenza la velocità di crociera |
|
Alpha 1 (Andata) |
1 anno luce |
0,6 anni luce |
|
Alpha 2 (Andata) |
2 anni luce |
1,2 anni luce |
|
Alpha 3 (Andata) |
3 anni luce |
1,8 anni luce |
|
Alpha 4 (Andata) |
4 anni luce |
2,4 anni luce |
|
Stazione Spaziale |
Distanza da Alpha Centauri misurata dal sistema di riferimento terrestre |
Distanza misurata dall’astronave appena ha raggiunto al ritorno la velocità di crociera |
|
Alpha 1 (Andata) |
1 anno luce |
0,6 anni luce |
|
Alpha 2 (Andata) |
2 anni luce |
1,2 anni luce |
|
Alpha 3 (Andata) |
3 anni luce |
1,8 anni luce |
|
Alpha 4 (Andata) |
4 anni luce |
2,4 anni luce |
Stop è sempre più perplesso...
Voi delle torri di controllo usate sempre i dati come meglio credete, ma non c’è alcuna spiegazione per giustificare queste misure così diverse.
Flash al contrario del fratello, invece è molto curioso e non ama gli atteggiamenti dogmatici.
Lui si sente un po’ come Giordano Bruno, ama volare e non solo fisicamente e i dogmi gli ricordano un po’ quel terribile rogo costato la vita a chi aveva osato mettere in discussione le indiscutibili certezze sposate dalla dottrina ecclesiastica dell’epoca.
Pertanto chiede ad Albert di spiegargli come tutto ciò sia possibile.
Il controllore non può fare a meno di ricordare che nel passato un suo omonimo aveva già spiegato quanto tempo e spazio fossero indissolubili e relativi.
Basta una semplice trasformazione per trovare la relazione tra il tempo proprio misurato con un unico orologio in un sistema di riferimento e quello improprio misurato da diversi orologi sincronizzati fra loro di un altro sistema di riferimento:
ΔT proprio = ΔT improprio/γ (dilatazione del tempo)
Dato che l’astronave viaggia a 0,8 c ci vuole un attimo per calcolare il valore di 1/γ
1/γ = √(1 – (v/c)2) = √(1 – 0,82) = √(1 – 0,64) = √0,36 = 0,6
ΔT proprio = ΔT improprio x 0,6
Applicando questa trasformazione è facile ricavare proprio i dati della prima tabella, ossia l'intervallo di tempo intercorso dalla partenza.
Infatti l’unico orologio dell’astronave segna un tempo proprio, mentre gli orologi delle stazioni spaziali sincronizzati con la Terra segnano un tempo improprio.
|
Stazione Spaziale |
Tempo improprio del sistema terrestre |
Tempo proprio dell’astronave ΔT proprio = ΔT improprio x 0,6 |
|
Alpha 1 (Andata) |
1,25 anni dalla partenza |
1,25 x 0,6 = 0,75 anni |
|
Alpha 2 (Andata) |
2,5 anni dalla partenza |
2,50 x 0,6 = 1,5 anni |
|
Alpha 3 (Andata) |
3,75 anni dalla partenza |
3,75 x 0,6 = 2,25 anni |
|
Alpha 4 (Andata) |
5 anni dalla partenza |
5 x 0,6 = 3 anni |
|
Alpha 3 (Ritorno) |
6,25 anni dalla partenza |
6,25 x 0,6 = 3,75 anni |
|
Alpha 2 (Ritorno) |
7,5 anni dalla partenza |
7,5 x 0,6 = 4,5 anni |
|
Alpha 1 (Ritorno) |
8,75 anni dalla partenza |
8,75 x 0,6 = 5,25 anni |
|
Terra 4 (Ritorno) |
10 anni dalla partenza |
10 x 0,6 = 6 anni |
Albert, oltre alla tabella, mostra anche un’animazione che riproduce il viaggio di andata e ritorno dell’astronave visto dal sistema terricolo e confronta il tempo proprio (dell’astronave) con il tempo improprio (della Terra e delle stazioni spaziali).
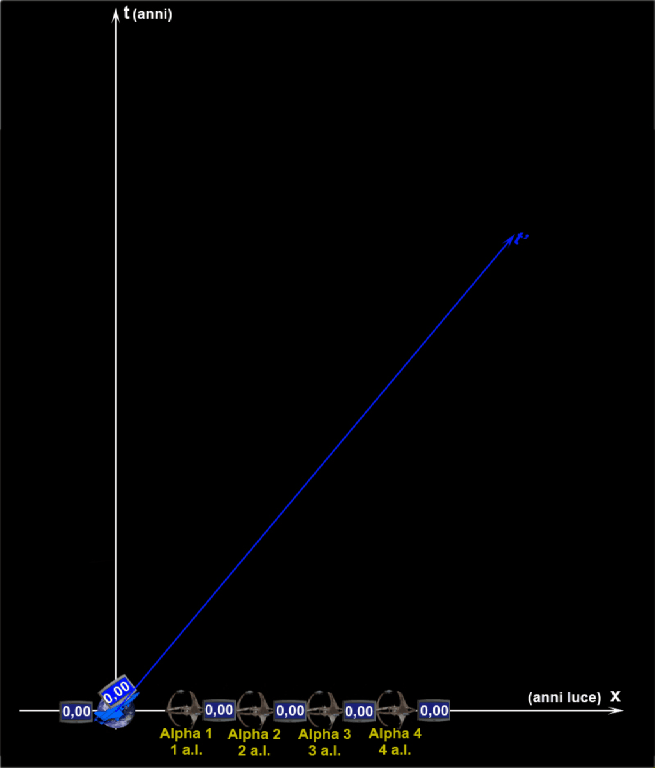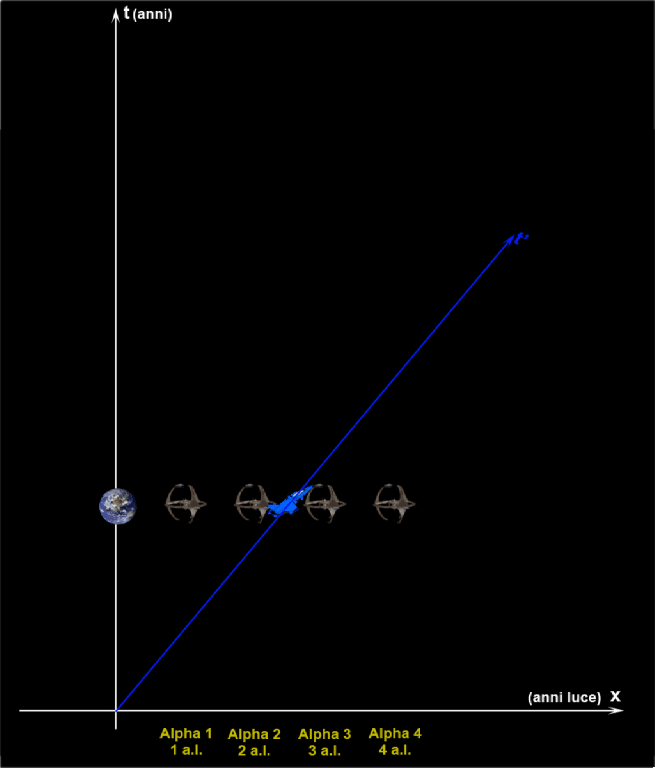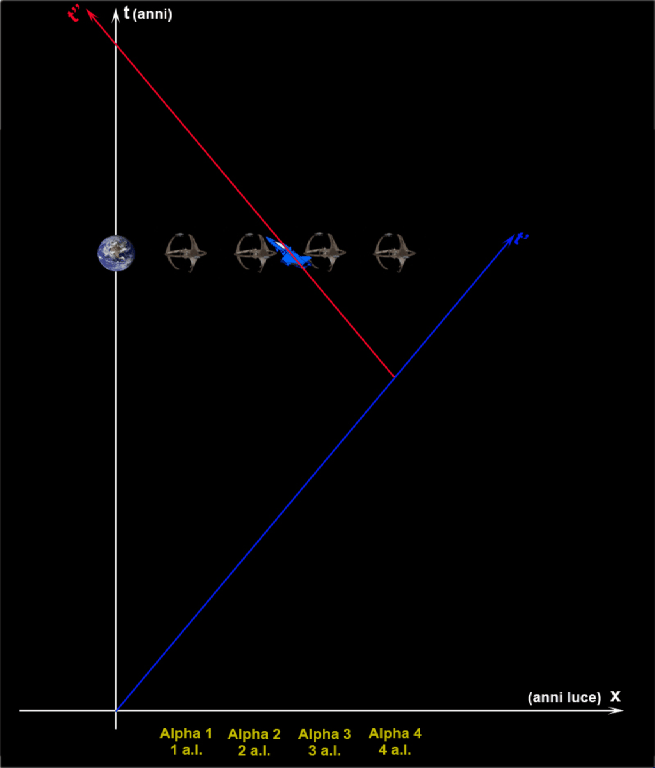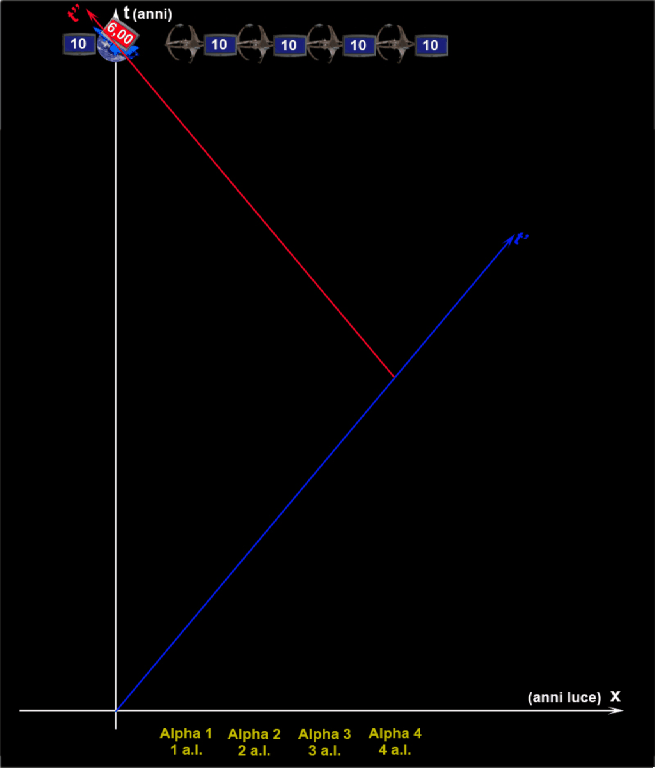
Dopo la spiegazione di Albert, i dati rilevati dalle varie stazioni spaziali durante il passaggio dell'astronave non appaiono più così misteriosi!
Albert però non ha finito.
Se cambia la misura del Tempo deve cambiare anche la misura dello spazio... d'altronde la velocità della luce è sempre la stessa per tutti i sistemi di riferimento.
Anche i dati della seconda tabella, dice Albert, non hanno nulla di misterioso.
Anche in questo caso è possibile applicare una semplice trasformazione per confrontare la misura della lunghezza (distanza) propria di un sistema di riferimento con la misura della lunghezza impropria di un altro sistema di riferimento.
La distanza tra la Terra e le stazioni spaziali è una Lunghezza propria dato che per la Terra ed il suo sistema di riferimento tale distanza non varia mai, mentre per l'astronave su cui viaggia Flash le stazioni spaziali si avvicinano a velocità pari all'80% di quella della luce, per cui la distanza si accorcia (lunghezza impropria) secondo la relazione:
L (lunghezza impropria) = Lo (Lunghezza propria) /γ = Lo x 0,6 (contrazione delle lunghezze)
Anche in questo caso, Albert ha una tabella da mostrare:
|
Stazione Spaziale |
Distanza dalla Terra misurata dal suo sistema di riferimento Lo (Lunghezza propria) |
Distanza misurata dall’astronave appena ha raggiunto alla partenza la velocità di crociera L (lunghezza impropria) = Lo x 0,6 |
|
Alpha 1 (Andata) |
1 anno luce |
1 x 0.6 = 0,6 anni luce |
|
Alpha 2 (Andata) |
2 anni luce |
2 x 0.6 =1,2 anni luce |
|
Alpha 3 (Andata) |
3 anni luce |
3 x 0.6 =1,8 anni luce |
|
Alpha 4 (Andata) |
4 anni luce |
4 x 0.6 =2,4 anni luce |
|
Stazione Spaziale |
Distanza da Alpha Centauri misurata dal sistema di riferimento terrestre Lo (Lunghezza propria) |
Distanza misurata dall’astronave appena ha raggiunto al ritorno la velocità di crociera L (lunghezza impropria) = Lo x 0,6 |
|
Alpha 3 (Ritorno) |
1 anno luce |
1 x 0.6 = 0,6 anni luce |
|
Alpha 2 (Ritorno) |
2 anni luce |
2 x 0.6 =1,2 anni luce |
|
Alpha 1 (Ritorno) |
3 anni luce |
3 x 0.6 =1,8 anni luce |
|
Terra (Ritorno) |
4 anni luce |
4 x 0.6 =2,4 anni luce |
Albert, ha anche rappresentato le diverse distanze rilevate dall’astronave, in una semplice figura.

Albert, non può fare a meno di rivolgersi a Stop: come vedi, oltre ad essere in perfetto accordo con i dati rilevati, nessuno ha viaggiato più veloce della luce... per l'astronave il tempo proprio di viaggio è più breve rispetto a quello improprio misurato del sistema terrestre, ma le distanze si sono accorciate.
L'aiuto controllore, un certo Sig. Lorentz, però non è molto soddisfatto dalla spiegazione fornita da Albert.
Mi sembra che manchi qualcosa, dice Lorentz.
Se non ricordo male, ogni sistema di riferimento dovrebbe misurare il tempo dell'altro come rallentato, ma allora come mai solo Flash al ritorno è più giovane?
Albert, non si scompone minimamente, poiché sa bene che Lorentz ha ragione.
Fortunatamente oltre all'astronave di Flash, ci sono molte altre astronavi in viaggio, che si muovono a velocità 0,8 c.
Tra queste Albert sceglie di contattare solo quelle che si muovono nella stessa direzione e verso dell'astronave su cui viaggia Flash.
In tal modo la distanza tra queste astronavi non cambia mai, per cui se gli orologi sono sincronizzati, queste rappresentano il sistema di riferimento di Flash, ovviamente diverso da quello della Terra (per il sistema Terra la distanza delle astronavi cambia continuamente).
Ora è il sistema di Flash che vede muovere spazialmente la Terra, le stazioni spaziali ed Alpha Centauri e che per misurare il loro moto deve usare orologi posti su astronavi diverse. Perciò, misura un tempo improprio con i suoi molteplici orologi posizionati sulle varie astronavi, mentre l'unico orologio della Terra misura un tempo proprio.
Quando l'astronave di Flash raggiunge Alpha Centauri, un'altra astronave del suo sistema di riferimento (stessa velocità in modulo direzione e verso) si trova in prossimità della Terra.
I loro orologi sono sincronizzati e la distanza tra queste astronavi non cambia mai, per cui entrambi gli orologi indicano che sono passati 3 anni dalla partenza.
Il pilota dell'astronave che si trova in prossimità della Terra vede chiaramente che mentre il suo orologio segna che sono passati 3 anni quello della torre di controllo terrestre indica che sono passati solo 1,8 anni dalla partenza.
Pertanto, per il sistema di riferimento delle astronavi solidali con Flash è il tempo proprio della Terra che si è dilatato (scorre più lentamente).
ΔT proprio = ΔT improprio/γ = ΔT proprio = ΔT improprio x 0,6 = 3 x 0,6 = 1,8 anni
Non a caso alla Torre di controllo terricola, durante il viaggio di andata, considerando i passaggi di Flash dalle stazioni spaziali, risultano i seguenti dati:
|
Stazione Spaziale |
Intervallo di Tempo improprio del sistema solidale con l’astronave di Flash (andata) |
Intervallo di Tempo proprio dell’unico orologio della Torre di controllo terricola ΔT proprio = ΔT improprio x 0,6 |
|
Alpha 1 (Andata) |
0,75 anni dalla partenza |
0,75 x 0,6 = 0,45 anni |
|
Alpha 2 (Andata) |
1,5 anni dalla partenza |
1,5 x 0,6 = 0,9 anni |
|
Alpha 3 (Andata) |
2,25 anni dalla partenza |
2,25 x 0,6 = 1,35 anni |
|
Alpha 4 (Andata) |
3 anni dalla partenza |
3 x 0,6 = 1,8 anni |
Albert, ha anche rappresentato in una semplice figura il viaggio di andata ed il confronto tra tempo proprio e tempo improprio, visto dal sistema delle astronavi solidali con Flash.
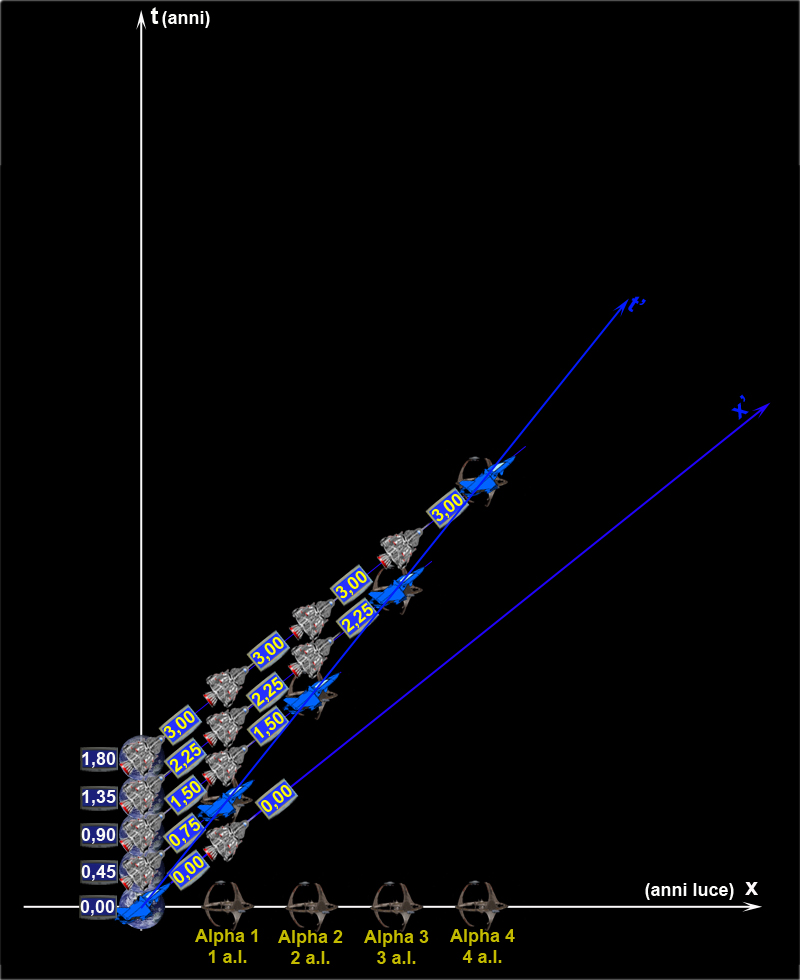
Una perfetta simmetria, afferma Albert: per il sistema di riferimento della Terra è il tempo dell'astronave che scorre più lentamente, mentre per il sistema di riferimento delle astronavi è il tempo della Terra che rallenta.
Una simmetria destinata a rompersi con l'inversione di rotta dell'astronave, esclama Albert!
Quando l'astronave di Flash inizia il viaggio di ritorno, cambia il suo sistema di riferimento.
E' un po' come un'autostrada in cui le macchine viaggiano tutte alla stessa velocità costante, ma mentre quelle che viaggiano su una corsia mantengono sempre la stessa distanza fra loro (stesso sistema di riferimento) quelle che viaggiano nell'altra corsia, in senso inverso, mutano continuamente la loro distanza rispetto a chi viaggia nella corsia opposta (altro sistema di riferimento).
Pertanto dopo l’inversione di rotta, sono le astronavi che viaggiano verso la Terra a velocità 0,8c che viaggiano in solido con Flash e che rappresentano il suo nuovo sistema di riferimento.
Quando l'astronave di Flash riparte da Alpha Centauri verso la Terra a velocità di crociera di 0,8c, tra le varie astronavi che appartengono al nuovo sistema di riferimento di Flash (ritorno) ve ne è una che si trova in prossimità della Terra.
Gli orologi di queste astronavi sono tutti sincronizzati e la loro distanza dall’astronave di Flash non cambia mai, per cui tutti gli orologi indicano che sono passati poco più di 3 anni dalla partenza.
Cambiando sistema di riferimento gli eventi che per Flash risultavano simultanei all’andata, non lo sono più al ritorno.
Infatti quando l’astronave di Flash raggiunge Alpha Centauri al termine del viaggio di andata, tra le astronavi appartenenti al primo sistema di riferimento (andata) i cui orologi sincronizzati segnano tutti 3 anni, quella in prossimità della Terra nota che l’orologio della Torre di controllo terrestre indica che sono passati 1,8 anni dalla partenza, mentre quando Flash inizia il viaggio di ritorno, tra le astronavi appartenenti al secondo sistema di riferimento (ritorno) i cui orologi sincronizzati segnano tutti 3 anni, quella in prossimità della Terra nota che l’orologio della Torre di controllo terrestre indica che sono passati 8,2 anni dalla partenza.
E’ un po’ come se durante la manovra di inversione di rotta, con il cambio di sistema di riferimento, per Flash il suo gemello rimasto a Terra sia invecchiato da 1,8 a 8,2 anni.
Un sorta di salto temporale!
Durante il ritorno, l'intervallo di tempo ΔT da considerare per il confronto tra tempo proprio (dell’orologio terricolo) e tempo improprio (degli orologi sincronizzati delle astronavi solidali con il percorso di ritorno di Flash) è quello che manca per raggiungere la Terra.
Quando Flash raggiunge la Terra, per la torre di controllo terricola sono passati 10 anni dalla partenza e questo è un evento certo.
Per l'astronave il percorso di ritorno non può che durare come quello di andata (visto che il modulo della velocità è lo stesso, ossia 0,8c), quindi per Flash mancano 3 anni per raggiungere la Terra.
Pertanto, usando il sistema di riferimento delle astronavi solidali con il percorso di ritorno di Flash, l’intervallo di tempo mancante per raggiungere la Terra è pari a 3 anni ed applicando la solita trasformazione, dove il tempo degli orologi del sistema delle astronavi è quello improprio e quello della torre di controllo sulla Terra è quello proprio, quest’ultimo risulta pari a:
ΔT proprio = ΔT improprio x 0,6 = 3 x 0,6 = 1,8 anni all’arrivo a Terra
Per ricavare il tempo che segna l’orologio della Torre di controllo terricola dalla partenza dell’astronave, e non quello che manca affinché l’astronave raggiunga la Terra, basta tener conto che quando Flash arriva a Terra, l’orologio terricolo deve segnare 10 anni.
Pertanto:
T proprio (dalla partenza) = 10 anni - ΔT proprio
T proprio (dalla partenza) = 10 anni – (3 x 0,6) = 8,2 anni dalla partenza.
Albert, mostra come tale indicazione sia in accordo con i dati rilevati:
|
Stazione Spaziale |
Intervallo di Tempo improprio del sistema solidale con l’astronave di Flash (ritorno) |
Intervallo di Tempo proprio dell’unico orologio della Torre di controllo terricola ΔT proprio = ΔT improprio x 0,6 T proprio (dalla partenza) =10 - ΔT proprio |
|
Alpha 4 (Ritorno) |
3 anni all’arrivo a Terra, 3 anni dalla partenza |
3 x 0,6 = 1,8 anni all’arrivo a Terra 10 - 1,8 = 8,2 anni dalla partenza |
|
Alpha 3 (Ritorno) |
2,25 anni all’arrivo a Terra, 3,75 anni dalla partenza |
2,25 x 0,6 = 1,35 anni all’arrivo a Terra, 10 - 1,35 = 8,65 anni dalla partenza |
|
Alpha 2 (Ritorno) |
1,5 anni all’arrivo a Terra, 4,5 anni dalla partenza |
1,5 x 0,6 = 0,9 anni all’arrivo a Terra, 10 - 0,8 = 9,1 anni dalla partenza |
|
Alpha 1 (Ritorno) |
0,75 anni all’arrivo a Terra, 5,25 anni dalla partenza |
0,75 x 0,6 = 0,45 anni all’arrivo a Terra, 10 - 0,45 = 9,55 anni dalla partenza |
|
Terra (Ritorno) |
0 anni all’arrivo a Terra; 6 anni dalla partenza |
0 x 0,6 = 0 anni all’arrivo a Terra 10 - 0 = 10 anni dalla partenza |
Albert, ha anche rappresentato in una semplice figura il viaggio di ritorno visto dal nuovo sistema delle astronavi solidali con Flash.
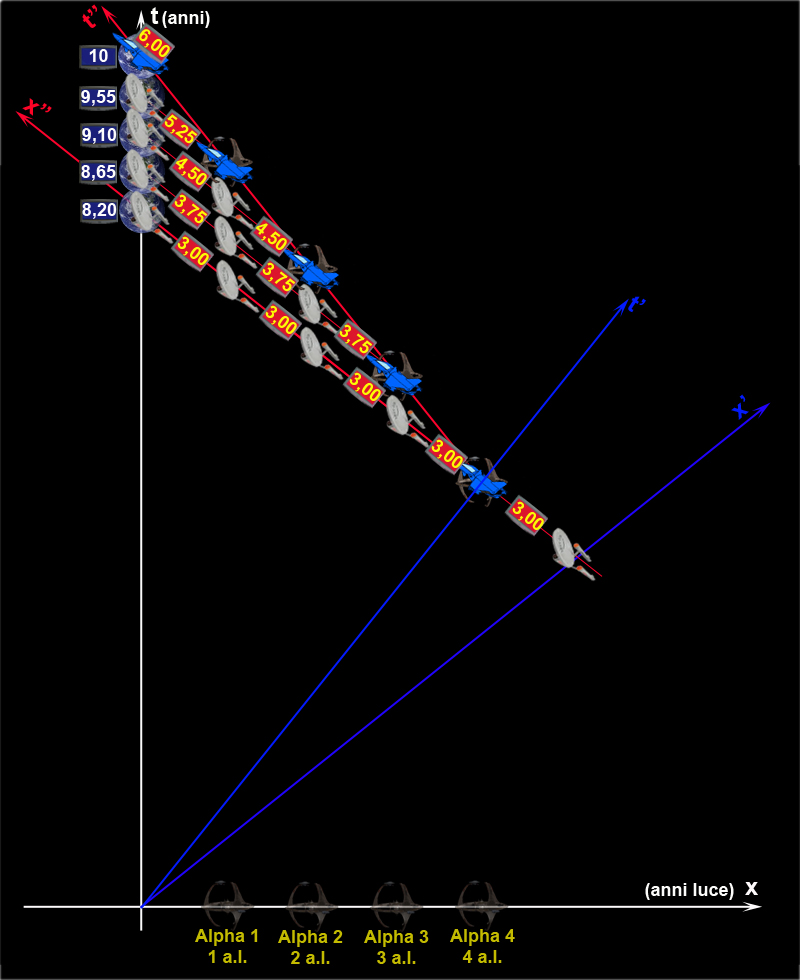
Infine, Albert mostra anche un’animazione che riproduce il viaggio, secondo il sistema delle astronavi solidali con Flash, sia all’andata, sia al ritorno con relativo cambio di sistema di riferimento.

Non è la velocità in sé che consente a Flash di tornare più giovane (anche perché se per la Terra è Flash che si muove, per Flash è la Terra che prima si allontana e poi si avvicina... non esistono sistemi di riferimento privilegiati), ma l'inversione di rotta ed il conseguente cambio del sistema di riferimento.
Ora anche Stop, nonostante i suoi pregiudizi, è costretto ad ammettere che se per lui sono passati 10 anni dalla partenza di Flash, per quest'ultimo ne sono passati solo 6!
L’andata e ritorno di Flash ha compiuto il miracolo di ottenere due gemelli, nati nello stesso giorno, ma che ora hanno ben 4 anni di differenza!
QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli






20 commenti
Il ragionamento è ben dettagliato e convincente.
Riprendendo l'affermazione conclusiva:
Non è la velocità in sé che consente a Flash di tornare più giovane (anche perché se per la Terra è Flash che si muove, per Flash è la Terra che prima si allontana e poi si avvicina... non esistono sistemi di riferimento privilegiati), ma l'inversione di rotta ed il conseguente cambio del sistema di riferimento.
è lecito affermare che se , invece di tornare indietro, l'astronauta Flash fosse atterrato su Alpha Centauri il suo sistema di riferimento sarebbe tornato a fissarsi con quello terrestre di Stop, e proprio in quell'istante, avrebbe incassato i 2 anni di ringiovanimento "potenzialmente" guadagnati durante il viaggio?
Aggiungerei che da quell'istante il suo tempo riprende a scorrere come quello del gemello sulla terra,essendo nel medesimo sistema di riferimento
Se poi, in un momento successivo, Flash decidesse di tornare, dovrebbe succedere la stessa cosa: arrivato sulla Terra, nel momento in cui abbandona il suo sistema di riferimento, fermandosi, guadagnerebbe altri due anni, accumulati nel percorso di ritorno.
caro Mau,
vi è sempre un cambiamento di sistema...
Certamente , è proprio quello che intendevo dire, sottolineando che di cambiamenti del sistema di riferimento se ne possono "vedere" addirittura due ( o forse un numero infinito se consideriamo le accelerazioni e decelerazioni nel loro divenire). In ogni caso il risultato resta quello, qualsiasi sia il numero di cambiamenti di sistema che immaginiamo abbia luogo.
Caro Mau, penso di aver capito cosa intendi.
Ti propongo, però, una variante inedita del cambio di sistema di riferimento.
Ammettiamo che Flash abbia appena raggiunto Alpha 4, che orbita intorno ad Alpherra.
Per lui sono passati 3 anni dalla partenza dalla Terra.
Per il suo sistema di riferimento (del percorso di andata), formato da infinite astronavi con gli orologi sincronizzati con quello di Flash (il gemello astronauta all'andata), l'astronave che passa dalla Terra ed il cui orologio segna 3 anni dalla partenza, vede il gemello Stop (quello rimasto a Terra) che è invecchiato di soli 1,8 anni.
Per Flash (o meglio per il suo sistema di riferimento all'andata) l'evento Stop invecchiato di 1,8 anni è simultaneo con lui che raggiunge Alpha 4 dopo essere invecchiato di 3 anni.
Mentre tale astronave passa dalla Terra, Stop si teletrasporta su questa astronave (cambia il suo sistema di riferimento).
Ora Stop è invecchiato di 1,8 anni, mentre Flash è invecchiato di 3 anni.
Per Flash è Stop che è più giovane (in questo caso è Stop che ha cambiato sistema di riferimento).
D'altronde in questo caso, Flash non ha cambiato sistema di riferimento (la sua velocità all'andate è costante, in modulo, direzione e verso), mentre Stop si.
Se ho detto qualche cavolata sono sicuro che Enzo mi correggerà.
Paolo
Secondo me si sta girando attorno a un non problema. Io posso anche teletrasportarmi (ma non è chiaro cosa questo significhi realmente) sull'astronave di un altro sistema, ma in quel momento divento parte dell'altro sistema e nulla cambia. Se in quel momento passa un altra astronave del sistema Flash vede Flash che è diventato Stop, tale e quale a quello che il nuovo stop (che prima era un flash) vedeva quando era un flash. Non mi sembra che sia cambiato niente... chi va con la Terra è sempre uno stop e chi va con Flash è sempre un Flash.
Se flash vero torna a terra e si ferma, diventa uno stop e non esiste più nessun sistema flash.
secondo me l'unica cosa da tenere ben presente è l'invariante. Qualsiasi giro si faccia spostandosi nello spazio si rimane sempre più giovani di chi si è mosso solo nel tempo. I salti temporali sono sempre qualcosa di fittizio.La RG risolve velocemente la questione: chi accelera sente un campo gravitazionale e il suo orologio non può più cambiare e riallinearsi tornando indietro. Nella RG la simmetria non esiste più... Tutto il resto è un modo per giungere a una conclusione simile senza entrare nella RG.
Egr. Prof. V. Zappala,
condivido il suo/vostro sentimento "i rudimenti della relatività dovrebbero essere una conoscenza introdotta nell'educazione di base" ma questo non è (stato, almeno per me). Adesso, in pensione, ho tempo libero e ho voluto colmare questa (mia) lacuna. Quindi sono un neofito e mi scuso per la banalità della domanda. Ho provato a vedere se il "salto temporale" (o, se preferisce, "il tempo AB inesistente" indicato in altro articolo) pari a 6,4 moltiplicato per l'inverso del fattore di Lorentz, nell'esempio uguale a 0,6, tra l'altro costante durante i viaggi di andata e ritorno) fosse uguale al tempo mancante all'orologio dell'astronauta (10-6=4). 6,4*0,6=3,84 ... quasi (scherzo). Dov'è il mio errore concettuale?
Grazie per la sua attenzione, cordiali saluti, Giacomo
caro Giacomo,
grazie per seguirci (guai a spegnersi con la pensione... io ho cercato di accendere tutte le lampadine possibili!)
il salto temporale di cui parli tu va calcolato nel seguente modo:
l'evento simultaneo all'arrivo dell'astronauta su Alpha risulta essere t = 1.8 anni nel sistema terrestre. Questo valore va diviso per 0.6 e ci dona proprio 3 anni che è uguale al tempo proprio impiegato dall'astronauta. L'evento arrivo è però identico a quello di inizio del ritorno da Alpha, ma in un sistema diverso, per il quale l'evento simultaneo risulta avere un t = 8.2, ossia 10 - 8.2 = 1.8 (perfettamente simmetrico all'andata). Se ne deriva un altro intervallo di tempo di 3 anni propri per giungere a Terra. Ne segue che per l'astronave il tempo passato è 3 + 3, mentre per la Terra è sempre 10.
Nell'articoletto in cui io avevo usato l'iperbole di calibrazione, si lavora sempre con tempi propri e quindi la differenza tra tempo terrestre proprio e somma dei tratti di andata e ritorno (propri) risulta proprio 4 anni. Lavorando con tempi propri non vi è bisogno di correzione, che è già tenuta in conto dall'iperbole che segna le unità di tempo proprio per qualsiasi velocità.
Ciao Vincenzo (sono passato al tu ... con qualche brontolio della mia educazione).
Grazie della risposta. Ho chiaro (almeno credo) l'uso dei tempi propri ed il fattore di Lorentz. La mia ambizione piuttosto era di cercare una relazione tra il salto temporale (4 anni) e la velocità dell'astronave che compie una rotazione istantanea. Io continuo a riflettere ma nel caso tu avessi già la risposta ... Saluti. Giacomo
Ciao Giacomo,
il prof. non può risponderti perché in questo periodo è assente (lo abbiamo scritto QUI), ma può darsi che possa farlo qualcuno dei collaboratori. Inoltro la tua domanda a chi di dovere, abbi solo un po' di pazienza... grazie.
Ciao Giacomo, spero di aver ben compreso la tua domanda.
4 anni non è altro che la differenza tra il tempo misurato dal gemello rimasto a Terra (10 anni) e i tempi di andata (3 anni) e ritorno (3 anni) misurati dal gemello astronauta (6 anni in tutto).
Tieni conto, però, che se il gemello astronauta invece di tornare indietro avesse proseguito nel viaggio di allontanamento da Terra, si sarebbe mantenuta la simmetria, ossia per entrambi i gemelli sarebbe stato il tempo dell'altro a dilatarsi.
In pratica, quando l’astronave raggiunge Alpha Centauri, per l’amico che si trova su Alpha 4, solidale con il sistema del terricolo, sono passati 5 anni, ma quando questo sbircia l’orologio dell’astronave si accorge che segna 3 anni (tempo proprio).
Cambiando sistema di riferimento, quando Alpha Centauri ha raggiunto l’astronave (per il gemello astronauta è Alpha Centauri che si avvicina), il gemello astronauta è costretto a rivolgersi ad un suo amico solidale per vedere cosa segna l’orologio della Terra e non a caso mentre gli orologi dei due amici solidali con l’astronave segnano 3 anni, quello in prossimità della Terra vede che l’orologio terrestre segna 1,8 anni (tempo proprio).
Il “salto temporale” (che non è la differenza di età tra i due gemelli al ritorno dell'astronave) invece, è legato all'inversione di rotta.
In pratica il gemello astronauta, quando inverte la rotta, cambia sistema di riferimento, ossia una volta giunto su Alpha Centauri per lui (il cui orologio segna 3 anni) risulta simultaneo l’evento corrispondente all’orologio terricolo che segna 1,8 anni, ma appena riparte, per il nuovo sistema di riferimento (ritorno) risulta simultaneo l’evento dell’orologio terrestre che segna 8,2 anni (10 – 1,8).
Volendo il “salto temporale” si può “diluire” mutando continuamente sistema di riferimento in caso di inversione di rotta, per cui cambia continuamente ciò che è simultaneo per il gemello astronauta, per il quale cambiano continuamente le linee di simultaneità, che mutano coprendo il salto temporale da 1,8 a 8,2 anni.
Qui trovi una rappresentazione di tale mutamento continuo.
Se ho mal compreso la domanda o se la risposta non è chiara chiedi pure…
Paolo
Dimenticavo, tieni conto che la figura che ho postato si riferisce ad una velocità di 0,9 c ed a una distanza di 4,13 anni luce, ma serve solo per mostrare cosa si intende per mutamento continuo delle linee di simultaneità in fase di inversione di rotta.
tieni conto che la figura che ho postato si riferisce ad una velocità di 0,9 c ed a una distanza di 4,13 anni luce, ma serve solo per mostrare cosa si intende per mutamento continuo delle linee di simultaneità in fase di inversione di rotta.
Paolo
Ciao Stefano,
Grazie! Illuminanti furono le parentesi! (4 anni) e (che non è la differenza di età tra i due gemelli al ritorno dell'astronave). Scusa ho sbagliato, il salto temporale è 6,4 anni. Avevo scritto giusto nella mia prima eMail. Invece, 4 anni è la differenza di età. Ovviamente non sono uguali e ... neppure legati dal fattore di Lorentz (troppo semplice). Avete ricavato la formula nel caso d'inversione istantanea dell'astronave? Ovviamente NON è importante, giusto una curiosità. Saluti. Giacomo.
Caro Giacomo, innanzitutto anche contraendo il nome Stefano è difficile ottenere il mio nome, ossia Paolo.
Ci sono molti modi per rispondere alla tua domanda.... e poi la curiosità è l'anima della conoscenza!
Tra i tanti modi ne ho scelto uno, che richiede un semplice ragionamento logico.
Facciamo finta di essere il gemello terrestre.
Ci sono due eventi che per il terricolo sono fissi, certi: la partenza del gemello astronauta e il suo ritorno.
Il gemello astronauta parte quando l'orologio del terricolo segna t=0 e torna quando il suo orologio segna t=10 anni.
Lascia perdere per un attimo quanto tempo passa per il gemello astronauta, ma anche per lui quando parte l'orologio della Terra segna t=0 e quando arriva segna t= 10 anni (quando si incontrano la realtà è quella per entrambi).
D'altronde, per il terricolo il gemello astronauta deve percorrere, tra andata e ritorno, 8 anni luce alla velocità di 0,8 c.
Basta la fisica classica per il gemello terricolo per calcolare quanto tempo impiega il gemello astronauta per percorrere tale distanza:
Δt = ΔS/V = 8/0,8 = 10 anni.
Un'ultima cosa, bisogna sempre ragionare per intervalli di tempo e di spazio!
Quando l'astronave raggiunge Alpha Centauri, per il gemello terricolo sono passati 5 anni:
Δt= ΔS/V =4 /0,8 = 5 anni.
Bene ora il terricolo usa il suo sistema di riferimento per capire quale intervallo di tempo segna l'orologio dell'astronave.
Per compiere questa operazione è costretto ad usare un suo amico su Alpha Centauri, il cui orologio è sincronizzato con quello del terricolo.
L'amico riferisce che quando l'astronave ha raggiunto Alpha Centauri l'orologio dell'astronave indicava un intervallo di tempo trascorso dalla partenza pari a 3 anni.
Perchè proprio 3 anni?
Semplice, basta applicare le trasformazioni di Lorentz.
Il terricolo, chiedendo aiuto al suo amico su Aplha Centauri per misurare il tempo di un altro sistema di riferimento, misura un tempo improprio (gli eventi simultanei per un sistema di riferimento non lo sono per l'altro), mentre l'orologio dell'astronave misura un tempo proprio.
Quindi:
ΔT proprio = ΔT improprio/γ = ΔT improprio x 1/γ
1/γ = √(1 – (v/c)2) = √(1 – 0,82) = √(1 – 0,64) = √0,36 = 0,6
ΔT proprio = 5 anni x 0,6 = 3 anni
In pratica il sistema di riferimento del terricolo misura la dilatazione del tempo dell'astronave.
A questo punto facciamo finta di essere il gemello astronauta.
Una volta che Alpha Centauri ci ha raggiunto (per noi è Alpha Centauri che ci viene incontro), il nostro orologio segna 3 anni (tempo proprio).
Tieni conto che per noi che vediamo Alpha Centauri avvicinarsi a v=-0,8c, la distanza non è di 4 anni luce (lunghezza propria misurata dal terricolo), ma di soli 2,4 anni luce (distanza misurata dall'astronave) e a dircelo è di nuovo il Signor Lorentz:
ΔL (distanza misurata dall'astronave) = ΔLo (Lunghezza propria)/γ
4 anni luce x 0,6c = 4 x 0,6 = 2,4 anni luce
Se vuoi puoi fare la prova del 9, ossia per l'astronave Alpha Centauri, che dista 2,4 anni luce (ΔS') ha impiegato 3 anni (Δt') per raggiungerci, ossia:
Δt' = ΔS'/V =2,4/0,8 = 3 anni.
Tornando al tempo, il gemello astronauta chiede aiuto ad un suo amico, solidale con lui il cui orologio è sincronizzato con quello dell'astronave, per cui segna Δt'=3 anni (quindi appartiene al suo sistema di riferimento, ossia per il gemello terricolo si muove verso Alpha Centauri con velocità v=0,8c) che si trova vicino alla Terra ed indica che l'orologio della Terra segna 1,8 anni.
Ora è il gemello astronauta che è costretto a rivolgersi ad un amico in prossimità della Terra, per cui misura un tempo improprio, mentre il terricolo misura un tempo proprio (quello del suo orologio)
A dircelo è sempre il Sig. Lorentz:
ΔT proprio = ΔT improprio x 1/γ = 3 anni x 0,6 = 1,8 anni
Ciò significa, che al termine del percorso di andata, per il sistema di riferimento del gemello astronauta è il tempo del terricolo che si è dilatato.
O meglio, per il gemello astronauta è passato un intervallo di tempo di 3 anni dall'evento certo partenza (t=0 e t'=0) ed il suo sistema di riferimento indica che invece per il terricolo sono passati solo 1,8 anni (dilatazione del tempo).
Per ora il gemello astronauta non ha ancora invertito la rotta.
Non resta che invertire la rotta e vedere cosa succede (consideriamo trascurabile il tempo impiegato dall'astronave per invertire la rotta... altrimenti vedi la figura postata prima che prova a diluire l'inversione...).
Se per l'astronave, prima dell'inversione di rotta Alpha Centauri si avvicinava a v=-0,8c, dopo l'inversione è la Terra che si avvicina alla medesima velocità v=-0,8c.
ΔL (distanza misurata dall'astronave) = ΔLo (Lunghezza propria)/γ
4 anni luce x 0,6c = 4 x 0,6 = 2,4 anni luce
La distanza misurata dall'astronave quindi è la stessa del percorso di andata, ossia la Terra dista 2,4 anni luce e si avvicina a v=-0,8c, quindi impiegherà un intervallo di tempo proprio di 3 anni per raggiungerci.
Ovviamente, dato che il modulo della velocità all'andata e al ritorno è lo stesso (cambia il verso), per il sistema di riferimento del gemello astronauta ad un intervallo di tempo improprio misurato grazie ai suoi solidali amici, corrisponde un intervallo di tempo proprio del gemello rimasto a Terra di 1,8 anni.
ΔT proprio = ΔT improprio/γ = ΔT improprio x 1/γ
ΔT proprio = 3 anni x 0,6 = 1,8 anni
Dunque a cosa corrispondono questi intervallo di tempo?
La soluzione è semplice.
Se c'è un evento certo è che quando l'astronave ritorna a Terra, l'orologio del gemello terricolo deve segnare t=10 anni (e questo vale per entrambi i gemelli).
Se per il sistema di riferimento del gemello astronauta mancano 3 anni per tornare da Alpha Centauri (3 anni andata e 3 anni al ritorno = 6 anni), a questo intervallo di tempo deve corrispondere un intervallo di tempo proprio terricolo di 1,8 anni:
ΔT proprio = ΔT improprio x 1/γ = 3 anni x 0,6 = 1,8 anni
Quindi per il terricolo mancano 1,8 anni affinché l'astronave torni a Terra.
Cosa segna l'orologio del Terricolo?
Semplice, se mancano 1,8 anni al ritorno dell'astronave, quando l'orologio terricolo segnerà 10 anni, non può che segnare che sono trascorsi 8,2 anni dalla partenza:
10 anni - ΔT proprio (terricolo) = 10 – 1,8 = 8,2 anni.
Ecco il salto temporale durante l'inversione di rotta...
Invertendo la rotta il gemello astronauta ha cambiato sistema di riferimento (cambia il verso della velocità, che è un vettore) e mentre il sistema di riferimento all'andata indicava che sulla Terra era trascorso un intervallo di tempo di 1,8 anni dalla partenza (tempo proprio terricolo), al ritorno indicava che sulla Terra mancava un intervallo di tempo pari a 1,8 anni al ritorno, per cui erano trascorsi 8,2 anni dalla partenza.
Come vedi il confronto tra l'età dei due gemelli rimane pari a 4 anni (10-6):
10 anni di tempo proprio per il gemello rimasto a Terra
6 anni di tempo proprio per il gemello astronauta
mentre il “salto temporale” misurato dal gemello astronauta durante il cambio istantaneo del suo sistema di riferimento durante l'inversione e di rotta è pari a 8,2 – 1,8 = 6,4 anni
Come vedi non c'è nulla di misterioso...
Spero così risulti più comprensibile... ma se rimangono dubbi, chieder non costa nulla...
Paolo
Caro Paolo (alias Stefano, scusa),
grazie, sì, sì tutto chiaro. Poi mi sono divertito un po':
durata viaggio = 2Г ; velocità = β = ν/c ; 1/γ = √(1 – β²) ; differenza età = Λ = 2 Г (1 - 1/γ)
asse tempi (t’): t β = x da cui Г β = X (spazio percorso a metà viaggio)
asse spazio (x’): t = β x + Y = ; Г = β X + Y ; Y = Г - Г β² = Г (1 - β²)
salto temporale = Ϫ =2 (Г – Y) = 2 Г β² ; ψ = fattore salto temporale
Ϫ ψ = Λ = 2 Г (1 - 1/γ) ; ψ = (1 – 1/γ) / β² = 1 / (1 + 1/γ) = γ / (1 + γ)
esempio n.1 : 2Г = 10 ; β = 3/5 ; 1/γ = 4/5 ; Λ = 2 ; ψ = 5/9 ; Ϫ = Λ / ψ = 18/5 = 3,6
esempio n.2 : 2Г = 10 ; β = 8/10 ; 1/γ = 6/10 ; Λ = 4 ; ψ = 5/8 ; Ϫ = Λ / ψ = 32/5 = 6,4
Non c'è presunzione nelle mie formule (d'altronde banali), solo un passatempo da pensionato. Errori?
Grazie ancora, buona giornata. saluti Giacomo.
Scusa Giacomo se rispondo solo ora.
Ti dirò che non mi è chiaro cosa intendi (magari è un mio limite ), soprattutto quando indichi che:
), soprattutto quando indichi che:
asse spazio (x’): t = β x + Y
Io preferisco legare le formule usate a specifici fenomeni fisici (tra l’altro parlare di rappresentazione dell’asse x’ e asse t in questo modo, a me crea qualche confusione con la descrizione dei due assi come rette nel diagramma di Minkowski, che non è proprio così… vedi qui: http://www.infinitoteatrodelcosmo.it/2015/10/01/lo-spaziotempo-di-minkowski-luniverso-in-un-foglio/).
Prima di iniziare vorrei fare una precisazione sulla dilatazione dei tempi.
Quando si dice che nella RR un sistema di riferimento misura il tempo di un altro sistema di riferimento come se questo rallentasse rispetto al suo (dilatazione dei tempi), è meglio chiarire che è cosa diversa da quello che vede un singolo osservatore.
Un sistema di riferimento consente di effettuare delle misure ed è formato da infiniti orologi sincronizzati fra loro (ma solo per quel sistema), posizionati a distanze conosciute, dato che tutto si muove in solido e le distanze non cambiano.
Usando un sistema di riferimento, per esempio, posso chiedere ad un altro osservatore solidale con me cosa segna l’orologio di un astronave che sta passando da quelle parti e confrontare cosa indicano i nostri orologi sincronizzati con quello che segna l’orologio dell’astronave.
Se proprio vuoi cerare una relazione matematica, ti propongo un metodo più semplice.
L’intervallo di tempo proprio, segnato dell’orologio terrestre, che indica la durata del viaggio di andata e ritorno è uguale a:
ΔT (Terra) = ΔX (andata)/β + ΔX (ritorno)/β = 2 ΔX/β
Dove ΔX è la distanza tra Terra ed Alpha Centauri
Nel nostro caso: ΔT (Terra) = 2 (4/0,8) = 10 anni
L’intervallo di tempo proprio che indica la durata del viaggio di andata secondo l’orologio dell’astronave, è uguale:
ΔT (astronave andata) = ΔT (Terra andata)/γ = (ΔX/β) 1/γ
Se aggiungo l’eguale percorso di ritorno ottengo:
ΔT (astronave) = ΔT (Terra andata)/γ + ΔT (Terra ritorno)/γ
ΔT (astronave) = (ΔX/β) 1/γ + (ΔX/β) 1/γ = (2 ΔX/β) 1/γ
Nel nostro caso: ΔT (astronave) = 2 (4/0,8) x 0,6 = 6 anni
Pertanto, al ritorno, quando i due gemelli si incontrano, la differenza di età è uguale alla differenza tra i due tempi propri:
ΔT (Terra) - ΔT (astronave) = 2 ΔX/β - (2 ΔX/β) 1/γ = 2 ΔX/β (1 - 1/γ)
Nel nostro caso:
Differenza di età = 2 (4/0,8) (1 – 0,6) = 10 – 6 = 4 anni.
Una piccola precisazione, cosa segna l’orologio dell’astronave al suo arrivo su Aplha Centauri (tempo proprio dell’astronave) ce lo dice l’osservatore solidale con il sistema terrestre che si trova su Alpha Centauri (attenzione che se per la Terra gli orologi del gemello terrestre e dell’osservatore solidale su Alpha centauri sono sincronizzati e segnano entrambi 5 anni, per l’astronave non lo sono).
Infatti, per il sistema di riferimento del gemello astronauta, quando alla fine del percorso di andata i suoi orologi segnano che è trascorso un intervallo di tempo di 3 anni, quello del gemello terrestre viene visto segnare un intervallo di tempo trascorso pari a 1,8 anni (dilatazione del tempo), mentre quello dell’osservatore solidale con la Terra che si trova su Alpha Centauri viene visto segnare 5 anni.
Ossia, misurato dal sistema del gemello astronauta, quando per lui è trascorso un intervallo di tempo di 3 anni (arrivo su Alpha Centauri), per il gemello terrestre ed il suo orologio è trascorso un intervallo di tempo di 1,8 anni:
ΔT(a) (Terra) = ΔT (astronave andata)/γ
E per l’intero percorso di andata e ritorno:
ΔT (a+r) (Terra) = ΔT (astronave andata)/γ + ΔT (astronave ritorno)/γ
ΔT (a+r) (Terra) = 2ΔT (astronave)/γ = (2 ΔX/βγ)/γ = 2 ΔX/βγ²
Questo intervallo di tempo è quello che segna l’orologio terrestre, visto primo dal sistema di riferimento dell’astronave all’andata e poi dal sistema di riferimento dell’astronave al ritorno (per cui a 3 anni misurati dal sistema di riferimento dell’astronave ne corrispondono 1,8 anni trascorsi sulla Terra ed in totale a 6 anni ne corrispondono 3,6).
Nel nostro caso: ΔT (ar) (Terra) = = 2 ΔX/βγ² =(2ΔX/β) 1/γ²= (2 x 4/0,8) x 0,6² = 3,6 anni
Ora non resta che calcolare il “salto temporale”, che non è altro che la differenza tra l’intervallo di tempo del viaggio di andata e ritorno misurato dalla Terra (ΔT (Terra)) e l’intervallo di tempo terricolo ΔT (ar) corrispondente alla dilatazione del tempo misurata dal sistema di riferimento del gemello astronauta (ΔT (astronave)).
ΔT (salto temporale) = 2 ΔX/β - 2 ΔX/βγ² = (2 ΔX/β) (1- 1/γ²)
Nel nostro caso: (2 ΔX/β) (1- 1/γ²)= 10 (1-0,36) = 6,4 anni
Il sistema sembra più lungo solo perché mi sono soffermato a legare ogni passaggio matematico ad un passaggio fisico.
Avrei potuto scrivere semplicemente:
ΔT (Terra) = 2 ΔX/β
ΔT (astronave) = (2 ΔX/β) 1/γ
Differenza di età = (2 ΔX/β) (1 - 1/γ)
ΔT (a+r) (dilatazione tempo terrestre misurato dal sistema astronave) = 2 ΔX/βγ²
ΔT (salto temporale) = (2 ΔX/β) (1- 1/γ²)
Paolo
PS: Ora che Enzo è tornato se ci sono imprecisioni sono sicuro che mi correggerà.
Giacomo, comunque, se vuoi prova a spiegare meglio da dove hai tirato fuori il ragionamento sull’asse x’ e t’ e su tutte quelle lettere greche che associ a dei parametri… così magari comprendo meglio quale procedimento hai usato.
Caro Paolo,
ti ringrazio della tua attenzione, ma non devi perdere troppo tempo con me. Mi sono divertito a costruire un po' di formulette e tutto è chiaro. Per soddisfare la tua curiosità:
I "miei" x' e t' sono proprio i due assi come rette nel diagramma di Minkowski,
Se scrivo t = β x + Y con la T maiuscola (T = β x + Y cioè l' asse dello spazio (x’) della figura 14 di http://www.infinitoteatrodelcosmo.it/2015/10/01/lo-spaziotempo-di-minkowski-luniverso-in-un-foglio/ come retta passante nel punto di metà viaggio, cioè il punto S2 dell'ultima figura di http://www.infinitoteatrodelcosmo.it/2018/01/11/soluzione-del-viaggio-alpha-centauri-del-paradosso-dei-gemelli-parte/ ) risulta più chiaro? L'incognita è Y e l'intersezione con l'asse dei tempi (t' uguale a T β = x) la determina univocamente. Poi ... semplici trasformazioni.
Domani studio bene le tue formule. Grazie ancora della tua attenzione. Saluti, Giacomo.
Caro Giacomo, penso di aver capito cosa hai fatto (anche se a me sembra che così si rendono le cose più complicate ).
).
Ammettiamo di usare la retta parallela all’asse x’ che passa per Alpha Centauri quando arriva l’astronave.
Tale retta indica gli eventi simultanei per il gemello astronauta, ossia rappresenta la sua linea di simultaneità quando “arriva” su Alpha Centauri.
L’equazione di tale retta, come mostra la figura 14 da te citata, è:
T = βx + T’/γ
Usando tale equazione è facile trovare quando la retta parallela all’asse x’ incrocia l’asse del tempo T, dato che tale asse è caratterizzato da punti aventi valore x =0.
T = β(0) + T’/γ
T = T’/γ
T’ non è altro che il tempo segnato dal sistema di riferimento del gemello astronauta quando “arriva” su Alpha Centauri, ossia 3 anni, pertanto:
T = T’/γ = 3 x 0,6 = 1,8 anni
Ossia, per il gemello astronauta, l’evento arrivo su Alpha centauri è simultaneo con l’evento orologio terrestre che segna 1,8 anni (questi due eventi giacciono sula stessa linea di simultaneità, quando gli orologi del sistema di riferimento del gemello astronauta all’andata segnano 3 anni).
Tu invece indichi T = βx + Y
Ma Y non è altro che T’/γ
Anche se alla fine arrivi alla stessa conclusione, mi sembra che così si complica il procedimento.
Tu ricavi Y (ossia T’/γ) sostituendo a x, la sua espressione ricavata dalla retta che descrive l’asse del tempo t’, ossia Tβ = x
T = βx + Y = β (Tβ) + Y = Tβ² + Y
Y = T - Tβ² = T (1 - β²) = 5 (1 – 0,8²) = 5 (1- 0,64) = 1,8 anni
Il “salto temporale” (Ϫ ) non è altro che la differenza tra la durata del viaggio misurata con il tempo proprio del gemello rimasto a Terra (10 anni) e l’intervallo di tempo terricolo corrispondente alla dilatazione del tempo misurata dal sistema di riferimento del gemello astronauta all’andata ed al ritorno (1,8 + 1,8 = 3,6 anni).
Ϫ = 2 (T – Y) = 2 (T – (T - Tβ²) = 2 (T – T + Tβ²) = 2 T β²
Ϫ = 2 x 5 x 0,8² = 6,4 anni
Λ = 2 Г (1 - 1/γ)
Ϫ ψ = Λ = 2 Г (1 - 1/γ)
In pratica ψ non è altro che il rapporto matematico (più che fisico) tra la differenza di età ed il “salto temporale”.
ψ = Λ/Ϫ
ψ = Λ/Ϫ = (2 Г (1 - 1/γ))/ 2 T β² = (1 - 1/γ)/β²
ψ β² = (1 - 1/γ)
ψ β² = (1 - 1/γ)….. moltiplico entrambi i membri per (1 + 1/γ)
ψ β² (1 + 1/γ) = (1 - 1/γ) (1 + 1/γ)…. è un prodotto notevole, ossia: (a+b) (a-b) = a² - b²
ψ β² (1 + 1/γ) = (1 - 1/γ²)
ψ β² = (1 - 1/γ²)/(1 + 1/γ)
0 = (1 - 1/γ²)/(1 + 1/γ) - ψ β²…. aggiungo ψ ad entrambi i membri
ψ = (1 - 1/γ²)/(1 + 1/γ) + ψ - ψ β²
ψ = (1 - 1/γ²)/(1 + 1/γ) + ψ (1- β²)
ψ - ψ (1- β²) = (1 - 1/γ²)/(1 + 1/γ) … ma (1- β²) = 1/γ²
ψ - ψ (1/γ²)= (1 - 1/γ²)/(1 + 1/γ)
ψ (1- 1/γ²)= (1 - 1/γ²)/(1 + 1/γ)
ψ = 1/(1 + 1/γ)
ψ = 1/(γ + 1)/γ
ψ = γ/(γ + 1)
Come dicevo, però, non assocerei un significato fisico a tale rapporto matematico.
Paolo
Caro Paolo,
tutto corretto (anche le osservazioni della tua ultima eMail).
Infatti, "traducendo la tua eMail di ieri" nei miei simboli:
ΔT (Terra) = ΔX (andata)/β + ΔX (ritorno)/β = 2 ΔX/β = 2 Г = durata viaggio
Differenza di età = (2 ΔX/β) (1 - 1/γ) = Λ = 2 Г (1 - 1/γ)
ΔT (salto temporale) = (2 ΔX/β) (1- 1/γ²) = 2 Г β² = 2 (Г – Y) = Ϫ
quindi: Ϫ ψ = Λ dove ψ = (1 – 1/γ) / β² = γ / (1 + γ)
E' vero, ero stato un po' sintetico ma ho solo cercato di usare le rette di simultaneità. ).
).
Nota: ho usato t (e non T) come ordinata dell'asse dei tempi vista la Figura 20 di http://www.infinitoteatrodelcosmo.it/2015/10/01/lo-spaziotempo-di-minkowski-luniverso-in-un-foglio/ (scusa, non so fare le figure con questo editor e non avevo modo di indicare 1/c come fece Minkowski ....
Certo, ψ è il rapporto tra la differenza di età e il “salto temporale” (cioè l'espressione cercata fin dalla mia prima eMail) e fornisce il "ringiovanimento" per unità di “salto temporale” . E' un significato fisico banale ma lo accetto volentieri.
ψ è anche un angolo sulla circonferenza di raggio β, essendo l'area del settore circolare individuata dalla metà della differenza delle unità di misura. ψ è un angolo normalizzato? Ulteriore significato fisico? Bohhh.
Grazie di tutto, al prossimo viaggio... Ciao, Giacomo.
Ciao, Giacomo.
Perfetto Giacomo, l’importante è capirsi.
Mi sono permesso di sviluppare il procedimento soffermandomi su ogni passaggio fisico e matematico per consentire a chiunque di seguire la discussione ed i ragionamenti…
Sicuramente si è persa la sinteticità, ma penso ne abbia guadagnato la comprensione.
A presto.
Paolo