Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento

 

In questo articolo cerchiamo di descrivere, in modo estremamente accurato, le condizioni che accompagnano il paradosso dei gemelli, basandoci essenzialmente sulla relatività della simultaneità e parlando soltanto di eventi. Assumiamo, ovviamente, come già dedotte le trasformazioni di Lorentz per passare da un sistema di riferimento a un altro e la rappresentazione nel diagramma di Minkowski. Abbiamo così in mano tutti i dati per poter risolvere, nel modo preferito, un paradosso che tale, in realtà, non è, ma deriva solo da una violazione della relatività ristretta. In particolare, si dimostra che una soluzione banale e ovvia si ottiene solo con almeno tre sistemi di riferimento (a meno di non passare alla relatività generale, dove il paradosso cessa di esistere).Vediamo, inoltre, come anche altri approcci trattati precedentemente abbiano pari valore e non si discostino molto uno dall’altro.

Consideriamo, in Fig. 1, come sistema “fermo” quello che contiene sia la Terra che Alpha Centauri.

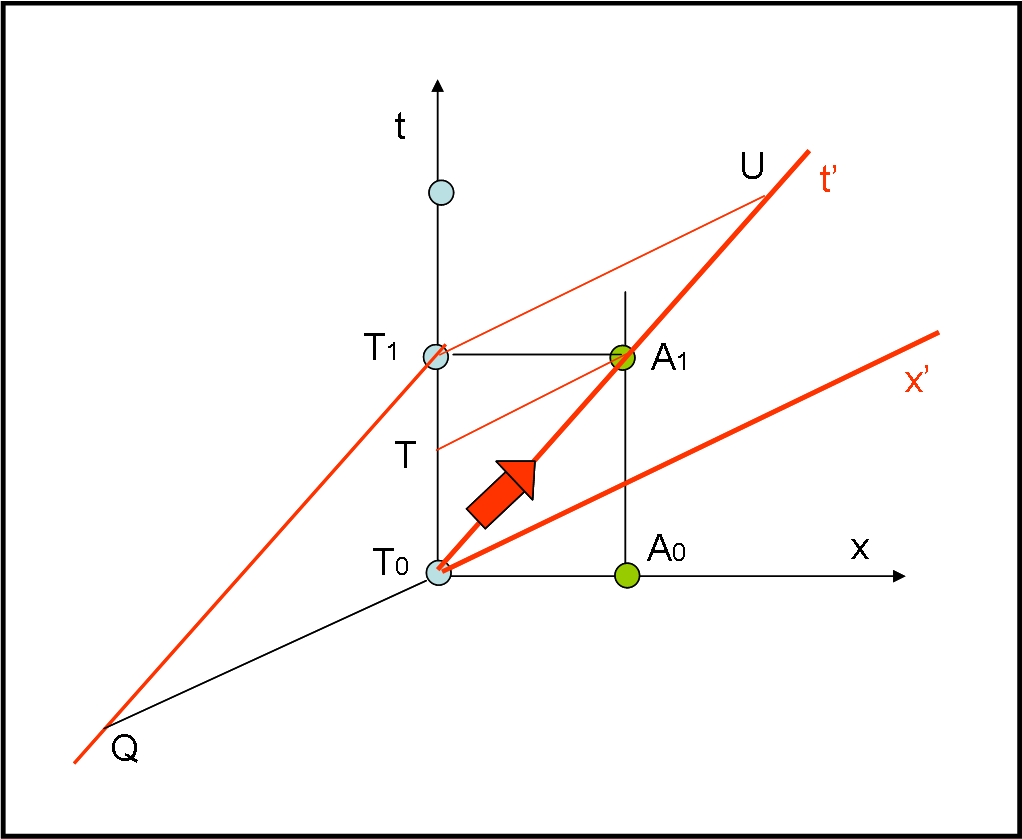
Le coordinate degli eventi in questo sistema S siano x e t. La Terra (azzurra) e Alpha (verde) sono, perciò separate solo da una distanza pari a 4 anni luce che si mantiene costante. I pallini azzurri sono eventi che hanno tutti la stessa distanza tra di loro (in particolare, 0) e quindi il tempo che si misura lungo l’asse t è un tempo proprio per questo sistema. Analogamente, i due pallini verdi sono eventi che mantengono la stessa distanza  (in particolare, 4 anni luce) e, quindi, anche la linea parallela a t che li unisce misura un tempo proprio. La differenza di tempo tra gli eventi T₁ e T₀ è un tempo proprio, così come la differenza di tempo tra gli eventi A₁ e A₀. Se l’evento T₁ ha la stessa t di A₁ gli eventi T₁ e A₁ sono simultanei, ad esempio t = 5 anni. Notiamo che abbiamo scelto come unità di misura, di x e t, l’anno luce e l’anno, in modo avere  c = 1.

Se volessimo andare da T₀ ad A₁ dovremmo impartire una certa velocità ad una ipotetica astronave, tale da percorrere (per esempio) i 4 anni luce in 5 anni, ossia tale da essere v = 0.8 c. Introduciamo, allora, un nuovo sistema di riferimento S’ solidale con l’astronave, di assi x’ e t’ (rossi). In questo sistema di riferimento il tempo si misura lungo t’ e le distanze lungo x’, per cui l’intervallo di tempo t’ che intercorre tra T₀ e A₁ diventa un tempo proprio. Notiamo, infatti, che la differenza di distanza tra gli eventi T₀ e A₁ rimane costante  (in particolare, 0).

Nel sistema S, la differenza tra i tempi t relativi agli eventi T₀ e A₁ è invece un tempo improprio, dato che i due eventi non hanno la stessa coordinata x (una è 0 e la seconda è 4). Analogamente gli eventi T₀ e T₁ non hanno la stessa distanza nel sistema S’ (la distanza si misura lungo l’asse x’): il primo ha x’ = 0, il secondo ha x’ = T₀Q = T₁U . Ne segue che la differenza di tempo t’ tra gli eventi T₁ e T₀ non è un tempo proprio. Lo sarebbe invece la differenza dei tempi  tra T₁ e Q oppure tra U e T₀

In maniera analoga si possono stabilire gli eventi simultanei nei vari sistemi. Nel sistema S l’evento T₁ è simultaneo all’evento A₁, mentre nel sistema S’ l’evento A₁ è simultaneo all’evento T, così come l’evento T₁ è simultaneo all’evento U e T₀ all’evento Q

In conclusione, impariamo una facile regola per riconoscere due eventi qualsiasi rappresentati in sistemi diversi: se in dato sistema la coordinata x (spazio) è la stessa, la differenza tra i due tempi corrispondenti misura un tempo proprio per tale sistema. Se, invece, i due eventi hanno la stessa coordinata temporale, i due eventi sono simultanei in tale sistema. In caso contrario, abbiamo tempi non propri o impropri ed eventi non simultanei.

Notiamo che stiamo parlando di sistemi riferimento, i quali sono caratterizzati da una miriade di orologi perfettamente sincronizzati dislocati per tutto lo spaziotempo, per cui non c’è bisogno, per un certo osservatore, di vedere direttamente un orologio di un altro sistema, distante spazialmente da lui (ossia attendere che la luce lo raggiunga), dato che c’è sempre un orologio del primo sistema vicino a lui.

Questa parte introduttiva è stata inserita per capire bene cosa s’intende per tempo proprio e tempo improprio: tutto dipende dalla differenza di coordinate misurate nei sistemi di riferimento. Detto in altre parole, tutto dipende dalla relatività della simultaneità degli eventi, la vera base di tutta la RR.

Fatte queste premesse fondamentali, possiamo cercare di affrontare il paradosso dei gemelli G (sedentario) e G’ (astronauta), basandoci solo e soltanto sulle coordinate dei vari eventi che caratterizzano il problema. Scoprendo presto che due sistemi non possono bastare, andiamo a calcolare tutte le coordinate degli eventi fondamentali in tre sistemi di riferimento, in modo da avere un quadro completo di tempi propri, impropri e di eventi simultanei. I sistemi sono S, quello terrestre e di Alpha; S’, quello relativo al viaggio di andata dell’astronave; S”, quello relativo al viaggio di ritorno dell’astronave sulla Terra.

Il sistema terrestre

Immaginiamo, allora. che un’astronave parta realmente per Alpha Centauri all’istante t = t’ = 0, così come rappresentato in Fig. 2 con una velocità di 0.8 c.

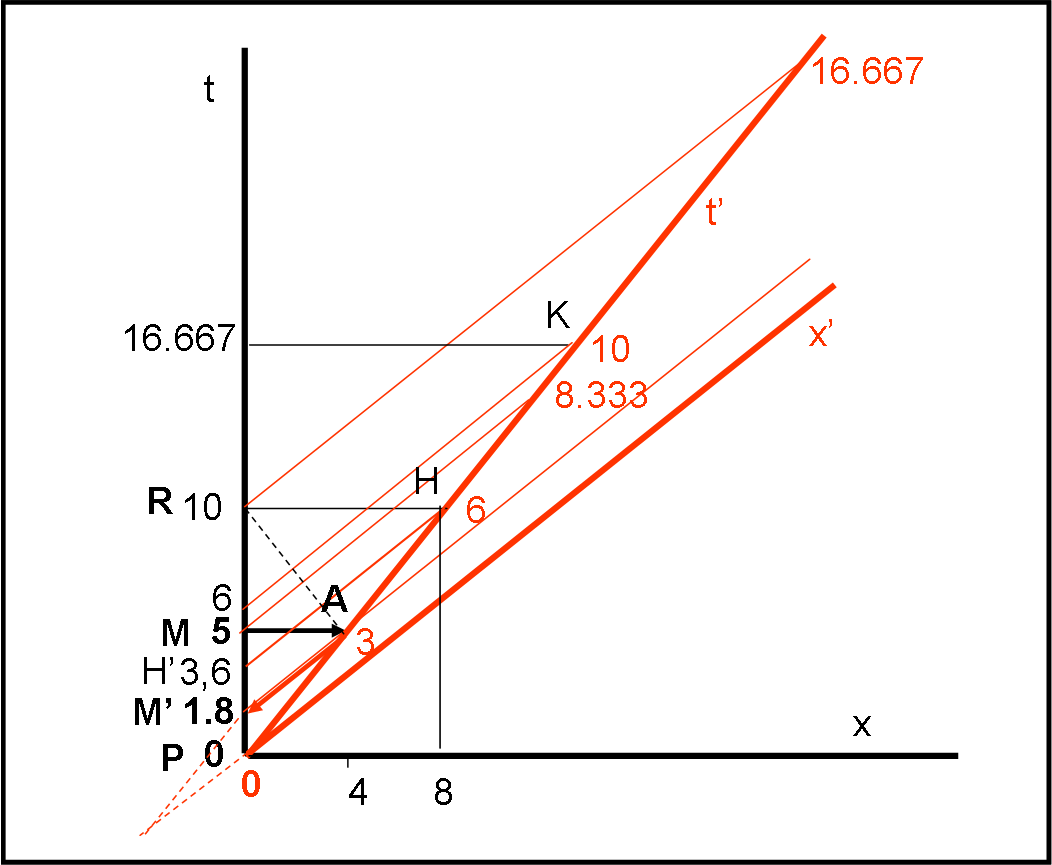
Calcoliamo subito il valore del fattore di Lorentz γ, che ci servirà presto e che ben conosciamo:

1/γ = √(1 – v²) = √1 – 0.8² = 0.6                  (c = 1)

Facciamo pure viaggiare l’astronave senza fermarla mai e cerchiamo di fare chiarezza sui vari eventi che ci possono interessare. I primi tre, i più ovvi, sono

L’evento P: partenza dell’astronave dalla Terra

L’evento A : arrivo dell’astronave su Alpha Centauri

L’evento R : ritorno dell’astronave sulla Terra

A questi ne aggiungeremo altri, un po’ alla volta

Richiamiamo le trasformazioni di Lorentz che permettono di passare dal sistema di riferimento S’ (viaggio di andata) al sistema terrestre S (e viceversa).

x’ = γ(x – vt)                                      …. (1)

t’ = γ(t – vx/c²) = γ(t – vx)                 …. (2)

Consideriamo gli eventi P, A, R nel sistema di riferimento terrestre S. Essi sono definiti dalle coordinate (x, t) e risulta, immediatamente:

P_S (0,0)

A_S (4,5)

R_S (0,10)

Esse si derivano facilmente, calcolando il tempo necessario all’astronave per raggiungere Alpha e per tornare indietro nel sistema S. La velocità è 0.8, per cui il tempo per arrivare su A che dista 4 anni luce, deve essere 5 anni. La stessa cosa succede per tornare indietro. Notiamo subito che il tempo che trascorre andando da R_S a P_S è un tempo proprio. Ci torneremo sopra molte altre volte, dato che vogliamo fare le cose in modo ultra accurato, calcolando anche coordinate non veramente necessarie, in modo da permettere approcci anche diversi.

Aggiungiamo subito l’evento mediano M (evento in cui da Terra si considera che l’astronave sia arrivata in A)

M_S (0,5)

Possiamo subito dire che, nel sistema, S l’evento M è simultaneo ad A (stesso tempo) e che tra lui e gli eventi di partenza e di arrivo, gli intervalli temporali sono ancora  tempi propri. In poche parole, potremmo già concludere che l’orologio unico della Terra segna 10 anni tra partenza e arrivo dell’astronave (o astronavi… ?) e che nel suo sistema l’astronave arriva su Alpha dopo 5 anni. Tuttavia, il tempo t trascorso per andare dall’evento P all’evento A non è un tempo proprio nel sistema S, dato che le rispettive x non sono uguali.

Spostiamoci, adesso, nel sistema S’ di coordinate x’ e t’

Il sistema del gemello astronauta

Calcoliamo gli stessi eventi di prima nel sistema di riferimento dell’astronave S’ utilizzando la (1) e la (2), dato che ormai conosciamo le loro coordinate x e t nel sistema S.

x’_P = γ(x_P – vt_P)

x’_P = (0 – 0.8·0)/0.6 = 0

t’_P = γ(t_P – vx_P)

t’_P= (0 – 0.8·0)/0.6 = 0

P_S’ (0,0)

Beh… questo era ovvio, dato che l’origine è comune ed è proprio P.

Passiamo all’evento A, le cui coordinate sono adesso calcolate nel Sistema S’

x’_A = (4 – 0.8·5)/0.6 = 0

t’_A= (5 – 0.8·4)/0.6 = 3

A_S’ (0, 3)

La differenza dei tempi tra gli eventi A e P nel sistema S’ è un tempo proprio, dato che la coordinata x’ è rimasta costante, in particolare 0. Ciò vuol dire, in altre parole, che basta un solo orologio dell’astronave per misurare l’intervallo di tempo trascorso.

Calcoliamo anche le coordinate dell’evento M (l’evento del sistema terrestre che corrisponde all’arrivo dell’astronave in A) in S’, ricordando che A e M sono simultanei nel sistema terrestre S.

x’_M = (0 – 0.8 ·5)/0.6 = - 6.6667

t’_M =  (5 – 0.8·0)/0.6 =    8.3333

M_S’ (- 6.6667, 8.3333)

 Se confrontiamo A_S’ (0. 3) con M_S’(-6.6667, 8.3333) ci accorgiamo subito che nel sistema S’ il punto A non è simultaneo a M. Ecco che compare il punto chiave di tutta la RR: non si mantiene la simultaneità tra due eventi le cui coordinate sono calcolate in sistemi inerziali diversi.  Nel sistema S’, l’evento simultaneo di A sull’asse del tempo t di S, deve avere la stessa t’ di A. Questo evento è sicuramente interessante e lo chiamiamo M’. Calcoliamo, innanzitutto, il suo t nel sistema terrestre (la x è zero per definizione)

Possiamo utilizzare la (2), ricavando la t corrispondente al valore t’ = 3

t’_M’ = γ(t_M’ – vx_M’)

3·0.6 = t_M’ - 0

t_M’ = 1.8

M’_S (0, 1.8)

Immediatamente, otteniamo le sue coordinate nel sistema S’, sapendo già che t’ = 3 (deve essere simultaneo ad A_S’)

x’_M’ = γ(x_M’ – vt_M’)

x’_M’ = (0 – 0.8·1.8)/0.6 = - 2.4

M’_S’ (- 2.4, 3)

Controlliamo, per sicurezza, gli eventi A e M’ nel sistema S’: A_S’ (0, 3) e M’_S’ (- 2.4, 3). Come previsto (e costruito) i due eventi hanno la stessa coordinata temporale e quindi sono simultanei.

Siamo giunti a un punto”imbarazzante”: L’astronave è arrivata su Alpha e tutto fila liscio con la RR che conosciamo, dato che stiamo lavorando con due sistemi inerziali. Non ci stupiamo di certo che il tempo proprio dell’astronauta sia risultato di 3 anni, mentre l’evento simultaneo al suo arrivo su Alpha, misurato nel riferimento S della Terra, sia di solo 1.8 anni. I due eventi P e M’ misurati in S’ non danno un tempo proprio (M’_S’(- 2.4, 3) e P_S’(0,0)), mentre è un tempo proprio per il sistema S, per il quale abbiamo M’_S (0,1.8) e P_S(0,0) (stessa coordinata x). La x’ dell’evento M’_S’ è individuata dalle linee sottili rosse tratteggiate.

L’astronave non può invertire la rotta

Non possiamo certo fare invertire la rotta della nostra astronave, dato che in questo caso passeremmo in un altro sistema inerziale dove le coordinate degli eventi cambierebbero nuovamente (per adesso almeno). Possiamo, però, tranquillamente continuare a far volare la nostra astronave lungo la sua traiettoria e vedere come misura, nel suo sistema S’, l’ultimo evento, calcolato precedentemente nel sistema S, ossia il punto R di ritorno dell’astronave previsto dalla Terra. La RR non può tradirci.

x’_R = (0 – 0.8·10)/0.6 = -13.3333

t’_R = (10 – 0.8·0)/0.6  = 16.6667

R_S’ (-13.3333, 16.6667)

Non stupiamoci queste strane coordinate. L’astronave se ne sta andando nello spazio e non può certo confrontare direttamente il suo orologio con quello del gemello rimasto sulla Terra, mentre noi volevamo che i due gemelli si incontrassero veramente. Risulta ovvio che il paradosso non ha senso se i sistemi di riferimento inerziali sono solo due: i due gemelli non si potranno mai incontrare. Tuttavia, potrebbero comunque confrontare i loro orologi! Ricordiamoci dei famosi orologi che dislocati ovunque in ogni sistema di riferimento.

Quello che potremmo fare è utilizzare un orologio solidale con la Terra che si trovi proprio lungo la traiettoria dell’astronave. Questo orologio misura lo stesso tempo di quelli terrestri. In altre parole, potremmo vedere che coordinate ha un evento H nel sistema S’ che sia simultaneo con l’evento R nel sistema terrestre: una specie di gemello terrestre “virtuale”

t_H = 10

x_H = 8

t’_H = γ(t_H – vx_H) = (10 – 0.8·8)/0.6 = 6 anni

Stupendo! Questo basterebbe a dirci che se l’astronauta percorresse due volte la distanza tra la Terra e Alpha (8 anni luce) (in fondo è del tutto equivalente ad andare e tornare) impiegherebbe solo 6 anni contro i 10 dell’orologio misurati dal sistema terrestre.  Purtroppo, questo ragionamento può essere immediatamente ribaltato…

Per capire che non abbiamo risolto un bel niente, basterebbe calcolare l’evento terrestre simultaneo all’evento H nel sistema di S’.

Per l’astronauta il punto H ha coordinate

H_S’(0, 6)

Qual è l’evento H’ simultaneo a H sull’asse t terrestre? Imponiamo che x_H’ = 0 (asse del tempo t)

t’_H’ = γ(t_H’ – vx_H’)

6 · 0.6 = t_H’

t_H’ = 3,6 anni

Accidenti! Se il sistema dell’astronauta avesse un orologio dei suoi, vicino a questo punto H’ si accorgerebbe che mentre per lui sono passati 6 anni, per l’orologio terrestre sarebbero passati solo 3.6 anni.

Ribadiamo che la RR funziona benissimo e che ogni gemello considera l’altro più giovane solo e soltanto per colpa di un diversa simultaneità. La faccenda è del tutto simmetrica: il tempo non proprio (ossia improprio) è legato a quello proprio corrispondente attraverso quel rompiscatole del fattore γ, che nasce proprio dalla simultaneità relativa degli eventi nei due sistemi

Lo possiamo vedere bene considerando l’evento K. Il tempo proprio dell’astronave vale 10, mentre l’orologio terrestre virtuale vicino a lui (sincronizzato con quello della Terra) segna 16.6667. Analogamente, però, quando l’orologio virtuale (sincronizzato con quello dell’astronave) è vicino a R (dove l’orologio terrestre indica 10) segna 16.6667. Nessuno dei due è più giovane dell’altro o, se preferite, lo sono tutti e due.

Un gemello in più

Non c’è niente da fare: per confrontare veramente l’età, gli orologi dei due gemelli devono venire a contatto: quelli virtuali seguono implacabilmente la RR e l’inerzia dei sistemi. Bisogna inventarsi qualcosa che non sia il solito cambio di direzione repentina che fa gridare allo scandalo molti lettori…

Dobbiamo far tornare l’astronauta sulla Terra per poter realmente vedere chi è il più vecchio, faccia a faccia. In qualche modo quei 3 anni che l’astronauta misura quando arriva su Alpha, devono conservarsi anche tornando indietro. Solo in questo modo potremmo concludere qualcosa di risolutivo.

In altre parole, l’astronauta dovrebbe misurare un tempo proprio di 6 anni tra andata e ritorno e verificare che, anche per lui, il gemello terrestre giungerebbe allo stesso evento dopo 10 anni di tempo proprio.

Il modo migliore è inserire un altro gemello G” che invece di partire dalla Terra, partisse da un luogo posto nel sistema Terra-Alpha, ma a 8 anni luce dalla Terra, con la stessa velocità del gemello viaggiatore G’. G” partirebbe nello stesso momento dell’altro (t” = t’ = 0) e arriverebbe su Alpha nello stesso momento di G’, con la stessa età.  Misurerebbe, però, tutti gli eventi posti sulla linea temporale della Terra in un sistema S”, anch’esso perfettamente inerziale.

La differenza fondamentale sarebbe che G” arriverebbe sulla Terra proprio al verificarsi dell’evento R. Potrebbe veramente confrontare il suo orologio con quello di G.

Cosa dovremmo fare in pratica? Considerare come gemello di partenza quello del sistema S’ (G’) e come gemello di arrivo quello del sistema S” (G”). Saremmo sicuri che, sostituendo G’ con G”, al loro arrivo simultaneo su Alpha, l’orologio del gemello G” misurerebbe veramente 6 anni nel momento dell’evento R. L’importante è verificare che per entrambi i gemelli viaggiatori il tempo passato sulla Terra sia veramente 10 anni. A quel punto il paradosso sarebbe risolto (con un piccolo trucco) e potremmo “fregare” la RR in modo truffaldino.

Non ce ne sarebbe nemmeno bisogno, ma per dare a tutti la possibilità di giocare con i vari eventi e riunirli in un unico schema, conviene ricalcolare tutti gli eventi del sistema Terra nel nuovo sistema S”. Nella Figura 3 il nuovo sistema è quello azzurro.

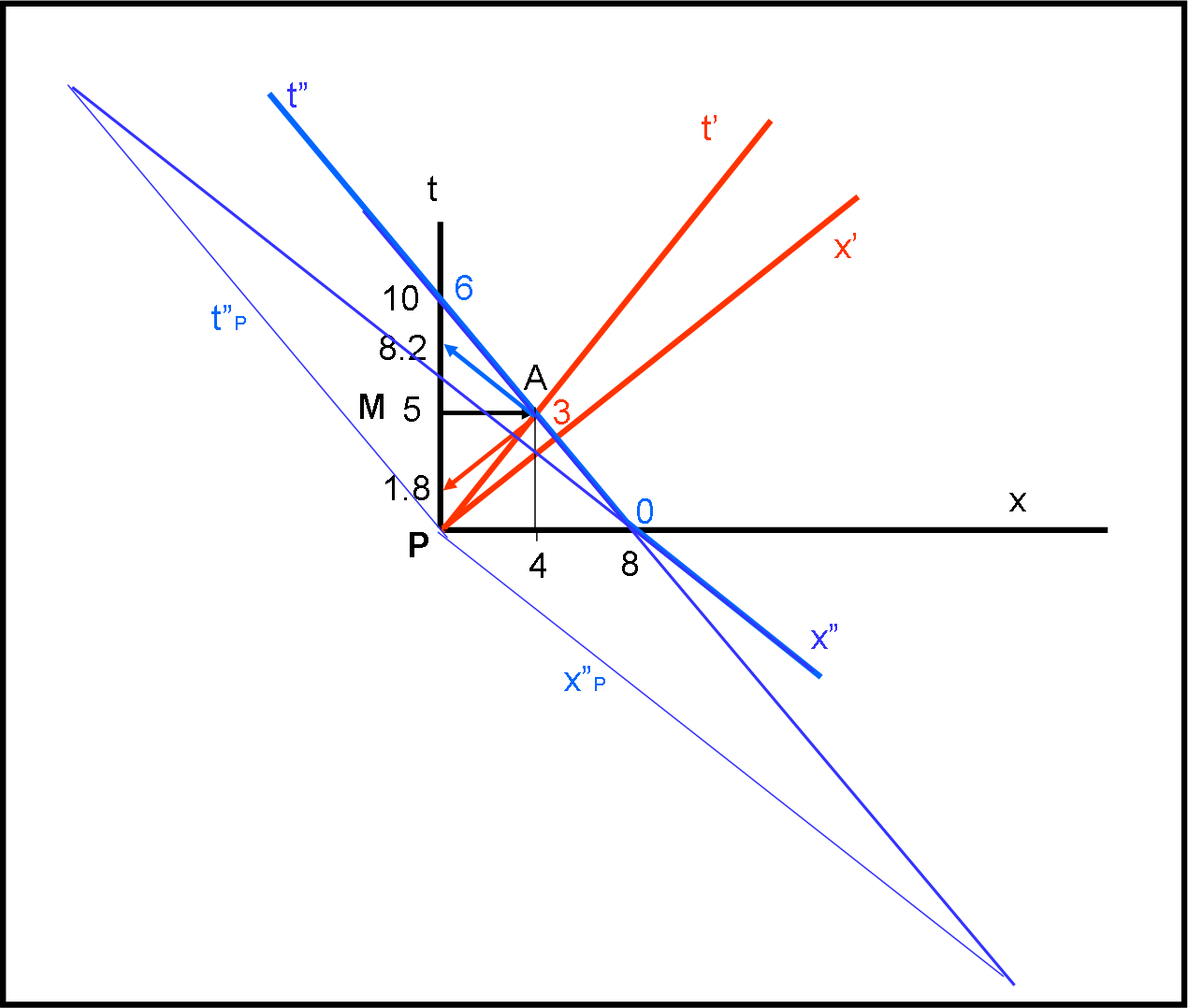
Le trasformazioni di Lorentz per passare da S a S” diventano:

x” = γ(x – 8 + vt)         …. (3)

t” = γ(t + v(x - 8))        …. (4)

Notiamo che x” = 0 per x = 8 e t = 0, così come t”, e la velocità ha, ovviamente segno invertito.

A questo punto possiamo ricalcolare tutte le coordinate degli eventi terrestri precedenti. Lascio a voi il compito (un lavoro di pura routine) e fatemi riportare solo i risultati finali:

P_S” (-13.3333, -10.6667)

M’_S”(-10.9333, -7.6667)

M _S”(-6.6667, -2.3333)

R _S” (0, 6)

A _S” (0, 3)

Abbiamo anche calcolato l’evento A e, come previsto, ci dice che il gemello G” arriva su Alpha con la stessa età e allo stesso istante di G’.

A questi aggiungiamo il punto M”, che altri non è che il punto dell’asse del tempo terrestre simultaneo ad A nel sistema di riferimento S” (analogo a M’ che è simultaneo ad A in S’). Lo calcoleremo anche in S e S’, per completezza.

M’’_S (0, 8.2)

M”_S’(- 10.9333, 13.6667)

M”_S”(- 2.4, 3)

Nella Fig. 3 sono indicate le coordinate di P_S”, per meglio comprendere come lavorare graficamente su sistemi non ortogonali… non è cosa molto banale e bisogna farci un po’ la mano (molto meglio fidarsi delle formule).

Il trucco

E’ giunta l’ora di fare una bella Tabella 1 con tutti gli eventi e le loro coordinate nei tre sistemi (ma non dite niente al gemello sedentario…), seguita dalla Fig. 4, che riporti i tempi calcolati nei vari sistemi di riferimento utilizzati.

 

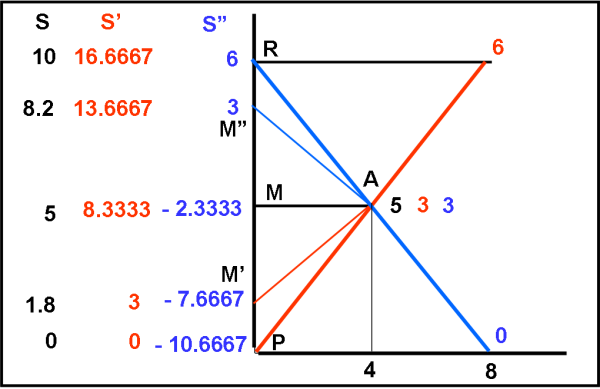
Innanzitutto, vediamo che quando G’ e G” si incontrano in A il loro orologio segna 3 ore. Questo vuol dire che, con un po’ di tecnologia avanzata, potrebbero scambiarsi gli orologi o, addirittura, cambiare astronave! G’, dopo aver fatto il viaggio fino ad Alpha, potrebbe spostarsi nell’astronave di G” e ritornare a Terra. Sarebbe proprio lui a confrontarsi con G e il trucco sarebbe solo quello di aver cambiato astronave (identiche, ovviamente). Purtroppo, G” se ne andrebbe nello spazio profondo. A voi (e a loro) la scelta.

Qualsiasi sia la decisione presa, il gemello (G' o G") che torna a Terra (evento R) è più che sicuro di avere impiegato 6 anni e il suo orologio lo dimostra (ha sempre calcolato un tempo proprio).

L’importante, adesso, è calcolare il tempo passato dal gemello G e verificare che sia proprio di 10 anni. Ma, deve essere 10 anni per tutti e tre i gemelli! Una garanzia fondamentale per concludere che essere rimasto più giovane è una realtà e non una strana magia.

Il gemello G fa in fretta a calcolare il suo tempo: i tempi dei vari eventi trascorsi sono stati tutti misurati con il suo orologio. Possiamo calcolare intervallo per intervallo o fare la differenza tra l’ultimo e il primo, ma il risultato non può che essere 10 anni.

Il gemello G’ (rosso) misura un intervallo di tempo tra R e P che risulta 16.6667. Però sa benissimo che è un tempo improprio rispetto a quello trascorso in S da G. Per trovare il tempo trascorso da G deve tener conto del fattore 1/γ. Ricordiamo che il tempo proprio si ottiene da quello improprio moltiplicandolo per 1/γ = 0.6. G’, quindi, per sapere il tempo proprio del gemello G non fa altro che scrivere:

t_RP = t’_RP 0.6 = 16.6667·0.6 = 10 anni

Perfetto, anche lui conferma che G è invecchiato di più.

Il gemello G” (azzurro) può fare lo stesso discorso e misurare la differenza di tempo tra R e P e poi moltiplicarla per 0.6. Il suo tempo improprio risulta

t”_RP = 6 - (- 10.6667) = 16.6667.

Com'era ovvio... è lo stesso misurato dal gemello G’. Facendo lo stesso calcolo di prima conferma anche lui che per il gemello G sono passati 10 anni.

Volendo essere ancora più raffinati, potremmo calcolare il tempo improprio di G’ da P ad A e trasformarlo in tempo proprio di G per arrivare a M. Non stupiamoci se esso risulta 8.3333 che diventa un tempo proprio di 5 anni. A questo punto lascia il campo al gemello G” (oppure lo calcola lui stesso se cambia astronave) e misura il tempo improprio per arrivare in R. Presto fatto: 6 - (-2.3333) = 8.3333. il che comporta un tempo proprio di G uguale nuovamente a 5 anni per andare da M a P. Ne segue, nuovamente, che anche per G” (o per G’ che ne ha preso il posto) il tempo trascorso da G è proprio 5 + 5 = 10 anni. Tutti sono d’accordo che il gemello viaggiatore che riabbraccia G rimane più giovane di ben 4 anni.

Conclusioni

Questo articolo è sicuramente un po’ strano… Vuole, in pratica, calcolare solo, in modo estremamente semplice, le coordinate di tutti gli eventi che possono essere utili per confrontare tre sistemi di riferimento inerziali. Non consideriamolo, quindi, difficile… dato che ci sono sempre due sole formulette da utilizzare. A questo punto abbiamo in mano tutti i dati per potere immaginare inversioni di rotta, salti temporali o quello che vogliamo. Io ho utilizzato un sistema un po’ truffaldino, ma non poi tanto se cambiamo astronave in A, per dimostrare che il paradosso si risolve solo e soltanto utilizzando tre sistemi di riferimento: siamo comunque riusciti a far incontrare i due gemelli iniziali e dimostrare che uno è realmente più vecchio. L’astronave che continua a viaggiare nello spazio dimostra, però, che con due soli sistemi di riferimento inerziali il paradosso non ha alcun senso, dato che la RR non perde affatto la sua simmetria.

Penso che possiate divertirvi a giocare con i  numeri che si sono ricavati nell’articolo e che i concetti di tempo proprio e di simultaneità siano stati (perfettamente) chiariti. Inoltre, visualizzare graficamente le coordinate che si ottengono facilmente con le trasformazioni di Lorentz è un esercizio che può dare molta soddisfazione (bravo Minkowski).

Possiamo considerare questa trattazione come quella iniziale o finale relativa al paradosso dei gemelli e forse quella che riesce a spiegare meglio tutte le stranezze che appaiono, cercando di non cambiare astronave.

Altri approcci

Tuttavia, il paradosso può essere affrontato in vari modi, come abbiamo già visto. Quello che io giudico più rapido e concettualmente più “professionale” è quello che si basa sull’invariante relativistico. Qualsiasi percorso si discosti da quello rettilineo che unisce due eventi, utilizzando un solo orologio (il tempo proprio), si effettua in un tempo minore. Nel caso dei gemelli, è quindi ovvio che il tempo proprio misurato dal gemello G sia più lungo di quello trascorso da una o due astronavi che vadano fino ad Alpha e poi tornino indietro. Addirittura, potremmo anche usare veramente una sola astronave tenendo conto di accelerazioni e decelerazioni e inversioni di marcia, integrando sul tutto il percorso e considerando sistemi di riferimento inerziali variabili continuamente (Fig. 5).

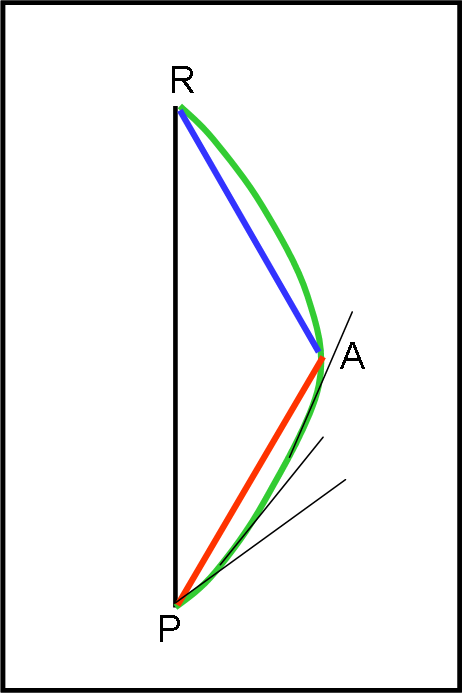
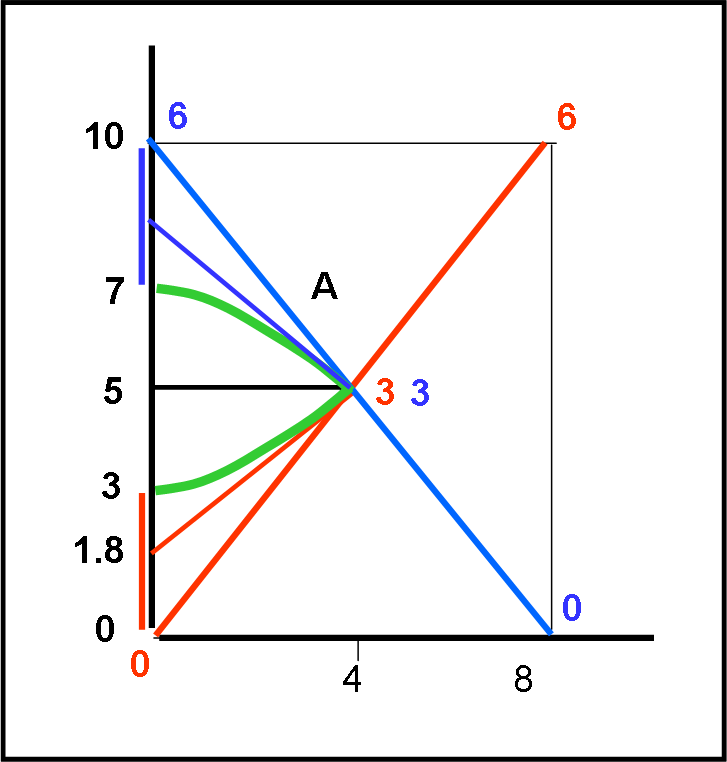
Nell’ambito dell’invariante relativistico non mi dispiace nemmeno la soluzione in cui si confrontano direttamente tempi propri utilizzando l’iperbole di calibrazione. Compare un salto temporale che sembra strano, ma che è il salto temporale effettivo lavorando solo con tempi propri (Fig. 6). In realtà, non è un salto temporale, ma il tempo proprio che manca al sistema "fermo" per pareggiare i due tempi propri del viaggiatore, In pratica è un semplice confronto di "distanze" spaziotemporali.

Come già detto, mi piace meno la soluzione che fa uso di … telescopi per vedere l’orologio del l’altro gemello. E’ sicuramente efficace, ma utilizza più che altro la velocità finita della luce e l’effetto doppler relativistico. In qualche modo mischia due effetti e non può assolutamente evitare che la RR entri in ballo in qualche modo. In ogni modo lo abbiamo usato anche noi, per non farci mancare niente.

I più teorici potrebbero dire: tutte approssimazioni o trucchi, il vero metodo è tenere in conto la relatività generale. Tutto si spiega durante l’inversione di marcia dell’astronave. Durante quella fase l’astronave decelera e accelera e quindi subisce una deformazione spazio temporale non simmetrica. L’orologio del terrestre che fino a un certo momento andava più lentamente, si mette a girare come un forsennato dato che quello dell’astronave sembra quasi fermarsi. Ma, come detto varie volte, è del tutto inutile infilarsi nelle equazioni della RG per un problema che si delinea molto bene anche senza di lei.

Infine, non trascuriamo nemmeno la favola di Muo1 e Muo2. In fondo, potremmo lavorare solo sulla contrazione delle distanze e ottenere la soluzione, non preoccupandoci più di tanto se la particella inverte la rotta. In fondo, si “raddoppia” la vecchia favola di Muo.

Direi che possiamo veramente chiudere con il paradosso dei gemelli. Cercheremo di mettere assieme gli articoli più indicativi e preparare un approfondimento il più esaustivo possibile.

 

QUI tutti (o quasi) gli articoli riguardanti il paradosso dei gemelli