Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Nella prima puntata di questa serie di articoli abbiamo parlato di spazi metrici, di bolle,di insiemi aperti e continuità. Il risultato più importante è stato quello di aver dimostrato l' equivalenza fra due distinte definizioni di continuità fra spazi metrici:la prima, che è la più conosciuta ed è la seguente:

Diremo che una funzione fra due spazi metrici f: X-->Y è continua in un punto p, se comunque prendiamo una Bolla di raggio ε e centro f(p) in Y , troviamo una bolla di raggio σ e centro p in X, tale che la sua immagine sia contenuta nella bolla scelta in Y:

detto in termini più formali:

Sia f:X-->Y una funzione fra spazi metrici; diremo che f è continua in  se per ogni >0 esiste un σ>0 tale che . Diremo poi semplicemente che f:X-->Y è una funzione continua se è continua in ogni punto p di X.

Ebbene, siamo riusciti a dimostrare che la definizione di continuità fra spazi metrici può essere data anche senza parlare di bolle e distanza, ma solo usando gli insiemi aperti:

Una funzione f: X-->Y fra  due spazi metrici è  continua se e solo se per ogni aperto A di Y,   è un aperto di X.

Il bello di questa definizione è che ci fa sganciare completamente dalla necessità di avere una distanza per definire la continuità, e di poterlo fare solamente avendo a disposizione delle famiglie di aperti. Ricordiamo che proprietà hanno gli aperti negli spazi metrici:

1.  (insieme vuoto) e X sono aperti
2. 2 se A1 e A2 sono aperti anche A1 U A2  è un insieme aperto; in generale se gli insiemi  al variare dell'indice i sono aperti , anche  è un insieme aperto
3. 3 Se A1, A2 sono aperti, anche l'intersezione  è un insieme aperto

Ebbene, se uniamo questi concetti possiamo arrivare alla definizione assiomatica di spazio topologico,che avevamo già anticipato nel primo articolo:

Una struttura topologica, o topologia su X è una famiglia t di sottoinsiemi di X tale che valgano le seguenti proprietà:

1. l’insieme vuoto e X appartengono a t;
2. l’unione di una qualunque famiglia di elementi di t appartiene ancora a t;
3. l’intersezione di un numero finito di elementi di t appartiene ancora a t.

Gli elementi di t sono detti  aperti della topologia , e gli elementi di X sono chiamati punti di X

La coppia (X,) si chiama spazio topologico.

Bene, adesso  siamo in grado di capire meglio questa definizione; gli spazi metrici sono spazi metrici ,e in essi possiamo definire gli aperti tramite le bolle; nella topologia abbiamo una struttura in un certo senso più povera, però molto più vasta; per dare una topologia ci basta dare questi insiemi che devono però soddisfare le proprietà 1,2,3 degli aperti. Ogni spazio metrico è uno spazio  topologico, non è però vero il contrario. Un paio di esempi per verificare quanto appena detto:

Primo esempio :

L'insieme delle parti P(X), ovvero l'insieme di tutti i sottoinsiemi di X è una topologia. Identifichiamo dunque i sottoinsiemi di X come nostri aperti.

1  (insieme vuoto) e X  sono sottoinsiemi di X

2 L'unione di qualsivoglia sottoinsiemi di X è ancora un sottoinsieme di X

3 L'intersezione di due qualsiasi sottoinsiemi di X è un sottoinsieme di X (che può essere anche vuota)

Secondo esempio :

Mettiamoci su R e consideriamo questa famiglia di insiemi:

={ (a,) ,con a} 

anche detta topologia la topologia delle semirette positive.

Vediamo che abbiamo  aggiunto   e R per soddisfare la prima proprietà.

Ma vediamo la seconda,  ovvero quella dell'unione:

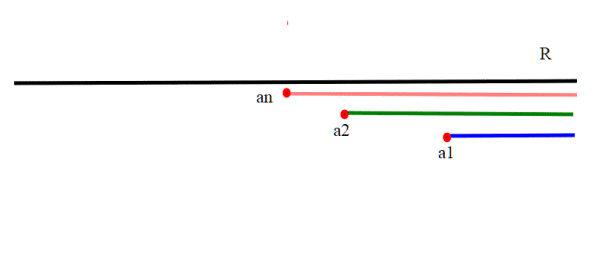
se devo infatti fare l'unione delle semirette colorate, mi  basta prendere quella con ai più piccolo (in questo caso an) per ottenere il risultato. Se invece devo fare l'intersezione sulle due semirette a1 e a2, basta prendere la semiretta con a1, che è il più grande dei due. In simboli: . In entrambi i casi otteniamo ancora delle semirette positive.

Topologia indotta

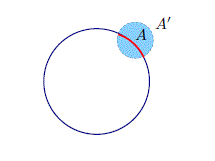
Quando si fanno delle trasformazioni, non sempre si prende tutto l0 spazio topologico, ma si considera solo un certo sottoinsieme. Esempio: più avanti tratteremo il cerchio e il quadrato, che sono sottoinsiemi del piano . Essi sono detti sottospazi topologici, ma con qual topologia? Sia X un insieme e S un suo sottoinsieme prendiamo come aperti l'intersezione dei sottoinsiemi  A di S con gli aperti A' di X. Esempi di aperti su un cerchio sono archi  con gli estremi esclusi, che possono essere ottenuti intersecando il cerchio con una bolla in 

Continuità negli spazi topologici

Come detto sopra, basta estendere quello che abbiamo visto per gli spazi metrici agli spazi topologici:

Una funzione f: X-->Y fra  due spazi topologici è  continua  se per ogni aperto A di Y,   è un aperto di X.

 Possiamo vedere con degli esempi che la continuità dipende strettamente dalla topologia, ovvero da come sono fatti gli aperti;

per esempio: sappiamo che la funzione  considerata in R-->R con la metrica usuale e quindi la topologia che da essa deriva, è una funzione continua; consideriamo invece la stessa funzione in  con la topologia delle semirette positive, definita sopra. Ebbene, con tale topologia la funzione non è continua. Infatti : che non è una semiretta positiva. Questo deriva semplicemente dal fatto che tutti i numeri minori di -1 o maggiori di 1 elevati al quadrato danno un numero maggiore di uno. Ma l'insieme di destra,, non è una semiretta positiva.

Nel prossimo articolo uniremo i concetti visti per arrivare agli oggetti più importanti della topologia: gli Omeomorfismi.