Categorie: Matematica
Tags: geometria monete quiz rotazione rotolamento
Scritto da: Vincenzo Zappalà
Commenti:51
Una moneta che rotola... non solo un QUIZ ***
In attesa di far rientrare in gioco Pippo e Pappo con il loro nuovo amico-nemico, dedichiamoci a cose un po' più astronomiche o, almeno, geometriche. Anche questo articolo sembra solo un quiz... In realtà lo è, ma ci permette di affrontare un argomento geometrico di grande interesse con chiari risvolti astronomici. Affrontiamolo con attenzione e ci sarà pane per tutti i tipi di denti. Tutto è partito pensando al simbolo del giorno di San Valentino... Scusate l'ermetismo, ma...
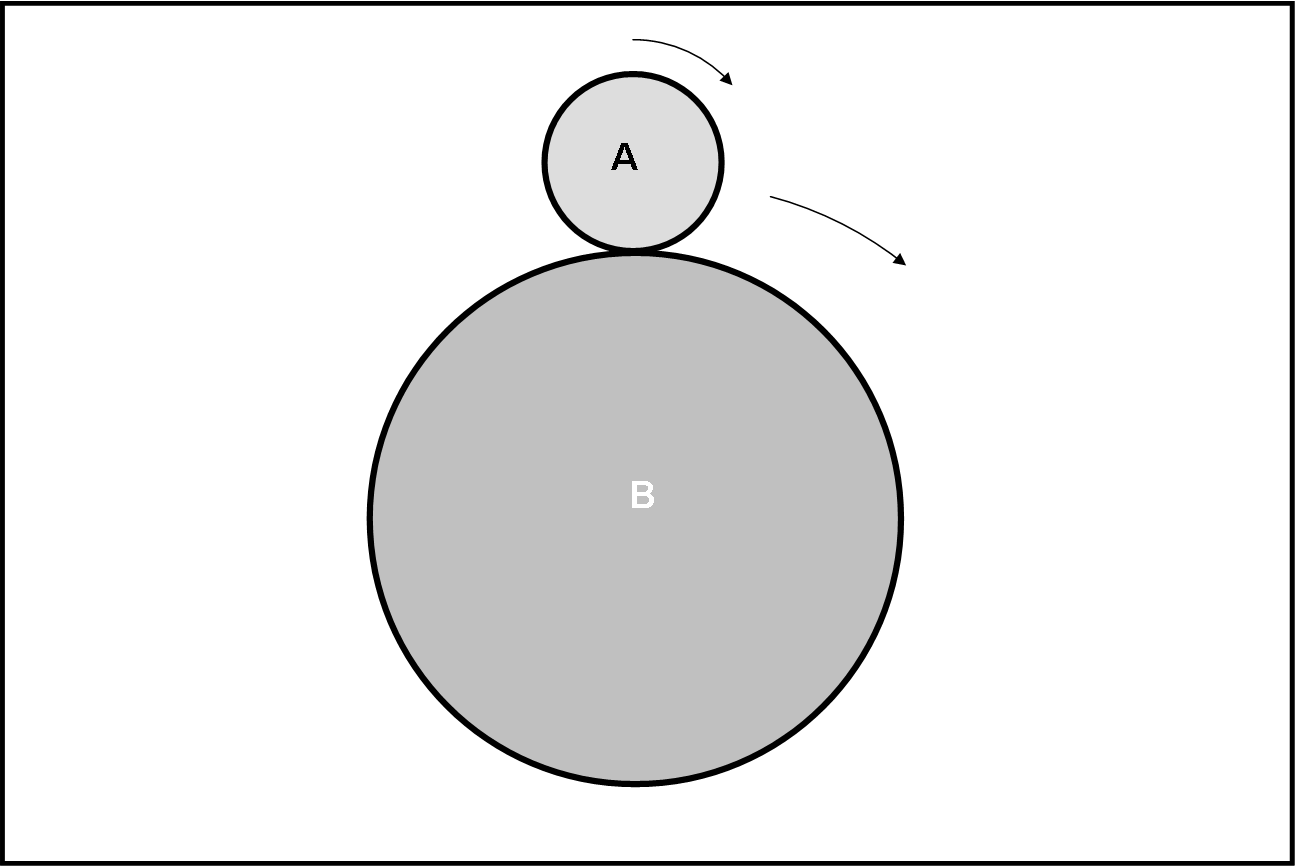
Il problema è estremamente semplice. Una moneta A ha il raggio che è 1/3 di quello della moneta B. La moneta A rotola senza strisciare attorno alla moneta B, che è fissa. Quante rotazioni esegue la moneta A dopo essere tornata al punto di partenza. Per rotazione si intende, ovviamente, il moto completo di un punto di una circonferenza attorno al centro della stessa. E' gradita anche la spiegazione e non solo un numero...
Per adesso nessun aiuto... ma pensate comunque all'Universo!
QUI la seconda parte del quiz
QUI la soluzione






51 commenti
Se la moneta piccola strisciasse senza rotolare compirebbe una rotazione completa. In più rotola pure, quindi ne fa 3 perché tale è il rapporto con la circonferenza fissa. Quindi, alla fine, di rotazioni complete ne fa 3 +1 = 4.
Anche la terra in un anno fa un giro in più su se stessa per il fatto di girare intorno al sole.
Temo di aver frainteso la domanda, visto che mi sembra troppo semplice... oppure c'è un tranello?
Comunque, se la domanda è: quante rotazioni compie la moneta A intorno alla moneta B per tornare al punto di partenza, la mia risposta è 3.
chissà se qualcuno mi fa vedere qualche bel disegnino e mi dice che argomento stiamo introducendo?
Credo proprio che Oreste abbia ragione... non ho pensato all'Universo (colpa gravissima!)
cara Dany,
la faccenda è un po' più complicata... pensa alla Luna...
Oreste, che è uomo di mondo, conoscerà sicuramente la ruletta (non quella del casino', anche se...)... Ne vedremo delle belle... Penso che Arturo ci vada a nozze!
L'avevo detto io che c'era il tranello...
Ok, ci penso, ma in questo contesto non si deve tenere conto del baricentro del sistema, giusto? Oppure sì?
metti il baricentro nel Sole e pensa solo all'orbita lunare ...
oppure -meglio ancora- pensa solo alla Luna e alla Terra. La moneta Luna cosa fa?
"oscilla" o qualcosa del genere... mi ricordo un quiz dedicato all'argomento e sto cercando di ritrovarlo nei meandri del blog (quello sfaticato di Scherzy si è preso un giorno di ferie e non mi vuole aiutare!).
Intanto, tra una ricerca e l'altra, ho trovato questa bella pagina di poesia, che non c'entra niente col quiz, ma vale la pena leggerla lo stesso
http://www.infinitoteatrodelcosmo.it/2014/04/16/dialogo-della-terra-e-della-luna/
Siamo tornati ai tempi antichi... deferenti ed epicicli. Ma ci interessano i casi particolari in cui l'epiciclo rotola esternamente al deferente. Dico bene Oreste???????
Veramente vuoi tirare in ballo i profili di "base" , "rulletta", i centri istantanei di rotazione etc etc, tutte quelle robe lì della meccanica razionale per descrivere i moti di rotazione ?
Sperando che non sia così, direi che una cosa che era implicita nella canzone di Modugno "selene ene ah" oltre al peso sulla luna (troppo approssimativo), poteva essere il fatto che la luna rivolge sempre la stessa "faccia" alla terra, quindi non rotola, semplicemente gira, e se fosse a contatto con la superficie terrestre questo giramento senza rotolamento lo chiameremmo strisciamento. Naturalmente lasciamo da parte i molti e complessi moti lunari e il loro influsso sul movimento della Terra. Il quiz dice che Il problema è estremamente semplice.
Oh mamma mia! Da un lato detesti Pippo e Pappo e adesso non vuoi nemmeno che parli di epicicli, epicicloidi e cose del genere... Uffa... ma allora di che parlo??!!!
Dai... non si trova spesso il moto della Luna descritto con tanto di deferente ed epiciclo, al pari di Tolomeo...
Per adesso siamo al primo passo: Luna e Terra. Ma se ci portiamo sul Sole... E io che pensavo mi dessi una mano.....

La deferenza è una cosa molto apprezzabile. Il deferente va ammirato e non bisogna rotolargli sopra, soprattutto con l'epiciclo,( ma neanche con il ciclo ). E più educato stare a una certa distanza, rotolargli esternamente, questo sì. Insomma sono d'accordo.
Argomenti alternativi di cui parlare, Enzone caro, ce ne sono tanti: per esempio potresti portare avanti la storia del calcolo della distanza Sole-Terra (ferma al viaggio di Cook nel XVIII secolo), oppure parlare di qualche altro corpo planetario "minore" che minore non è, oppure, per non impegnarti troppo, puoi sempre prendertela con riscaldamento globale e materia oscura...
ma se ti diverti di più a torturarci con i quiz che sono semplici solo nel tuo sistema di riferimento, fai pure poi, però, non stupirti quando un corteo organizzato dalla CGILAB (Confederazione Generale Italiana del Lavoro di Autori Blog) occuperà il tuo bel giardino e calpesterà quel rigoglioso cespuglio di salvia
poi, però, non stupirti quando un corteo organizzato dalla CGILAB (Confederazione Generale Italiana del Lavoro di Autori Blog) occuperà il tuo bel giardino e calpesterà quel rigoglioso cespuglio di salvia 
Va beh... mentre aspetto che mi passi a prendere il pullman della CGILAB, darò una rispolverata al sistema tolemaico
http://www.infinitoteatrodelcosmo.it/2016/08/10/i-racconti-di-ciccio-e-astericcio-appendice-alla-5-puntata-1-parte-la-nascita-della-ricerca-scientifica/
Bello il brano sul dialogo terra-luna. C'è anche un esempio di come si dovrebbe essere discreti, rispettare la praivasi e non fare pettegolezzi, con quella bellissima frase della Luna.... "Luna. Delle tue corna io non so che dire.."
Anche se ha delle informazioni si capisce che le tiene per sé. Brava Daniela!
L'articolo di ciccio e astericcio è, come sempre, delizioso, e alla fine parleremo sicuramente di Tolomeo marameo. Ma tornando per un momento alle monete (oggi quello che conta sono i soldi), se disegniamo le tre posizioni in figura ( la cicloidina 'n coppa al deferente è tracciata a sentimento e rappresenta la traiettoria del punto della monetina in contatto iniziale con la monetona - andrebbe ridisegnata altre 2 volte), vediamo che alla fine la monetina ha fatto 4 giri su se stessa. Oppure c'è un errore nel disegno e/o nel ragionamento?
Un bel sistema di riferimento per far vedere la quarta rotazione? E un puntacchio sulla monetina girovaga, nemmeno?
Hai mica avuto la vaga idea che di queste cose a Daniela non fr... interessa niente? Va bene, tornerò a Pippo e Pappo....
Più che vaga idea, l'ho ribadito più volte molto chiaramente sia a te che a Oreste che i quiz mi fanno venire il mal di stomaco, ma voi non ci credete
Almeno apprezza il tentativo (anche se puerile) di dare una risposta, con tanto di formulette Latex. Ti sei già dimenticato il mio primo commento???
Be' di Puntacchi sulla monetina ne ho disegnati non uno, ma infiniti, perché ho tracciato addirittura un raggio in colore blu che collega il centro con il punto iniziale di contatto. Questo raggio di colore blu n nel mentre che la monetina rotola su un terzo della monetona compie una rotazione di un giro completo PIU' una rotazione che vale 1/3 di angolo giro, dovuto al fatto che segue la curvatura della circonferenza della monetona.
Se la monetona avesse diametro infinito, la sua circonferenza sarebbe una linea retta e il raggio si allineerebbe nella posizione iniziale, senza alcuna rotazione addizionale. Ma non è così. C'è anche quel terzo di giro in più perchè il binario si è curvato di 120 gradi.
Se torni subito a Pippo e Pappo mi metto in malattia.
Sì, mi metto in malattia anche io. Bòja fàuss!
https://torino.diariodelweb.it/torino/articolo/?nid=20160311_377073
pfuiii... un bel sistema cartesiano fa vedere bene che il puntacchio sta anche ruotando una volta in più... ma tu sei sempre ermetico .... Ti meriti Pippo-Pappo-Nobody!!!!
E, per favore, cerca di dire a Dany di non strapparmi le lacrime...
Che ne direste di far vedere l'epicicloide della Luna per distanze diverse Luna-Terra.... che belle figurine!!!!! Mi ricorderebbero Tolomeo....
Va bene, va bene... vi lascio stare... prima che non rimanga più nessuno in questo Circoletto e Epocircoletto o cose del genere...
Ma come si fa a dire di no a questo professore... ?!?
Dai, MauPau, tu cerca di capire cosa vuole e se hai bisogno di supporto morale conta su di me!
(Per la serie "armiamoci e partite!" )
)
Caro Enzo,
io, senza sapere né leggere né scrivere, ho fatto questo ragionamento:
considero la circonferenza di raggio AB con
AB=(1+1/3)R=(4/3)R C=2π(4/3)R=(8/3)πR
quindi A (centro della monetina) ruotando rispetto a B (centro della monetona) compie un giro completo di lunghezza pari a (8/3)πR ;
il punto di contatto tra monetina e monetona compie un giro completo intorno ad A disegnando una circonferenza di lunghezza pari ad 2(1/3)πR = (2/3)πR e rapportando le due circonferenze:
[(2/3)πR]/[(8/3)πR]= 1/4
che significa che ad 1/4 di giro del punto A intorno al punto B, la monetina ha compiuto un giro completo intorno al suo centro A, quindi per ritornare nella posizione iniziale, la monetina compie 4 giri, con la condizione che la monetina giri intorno al proprio centro A e la monetona sia ferma rispetto al proprio centro B.
Perdona se ho scritto baggianate parziali o tutto lo scritto è una baggianata!
non mi convince tanto Andy (o forse non ho capito bene io). Sembrerebbe che quando A compia 1/4 di rotazione intorno a B (90°), la moneta piccola abbia completato il suo primo giro. In realtà non è vero, perché la monetina compie un giro completo dopo 120 gradi di rotazione di A attorno a B.
La faccenda si spiega meglio pensando alla Luna che non rotola, ma striscia soltanto, eppure...
secondo me se si disegna qualcosa sulla moneta (una faccia da schiaffi?) si vede meglio la quarta rotazione....
Basta prendere due monete vere uguali. Se si fa rotolare per mezzo giro una attorno all'altra si vede che ha fatto un giro completo. 180 gradi propri e 180 per il fatto che il binario si è curvato di mezzo giro
Pienamente d'accordo, ovviamente.... la formula è sempre giri = n + 1. Per la Luna: 0+1
Che ne dici della soluzione di Andy? Forse, forse ha ragione pure lui....
Va bene questa? (Intendo la faccia da schiaffi )
)
Nota bene: l'idea è di Mau che me l'ha commissionata perché non è casa in questo momento, ma io la sottoscrivo al 100% !!!
Concordo sul fatto che dopo 1/4 di giro la monetina ha compiuto 3/4 di giro di suo e, per via del binario che si è curvato di 90 gradi, si riallinea alla posizione iniziale. La cosa si ripete altre 3 volte fino a completare il giro
Caro Andy,
ti chiedo SCUSA! Ragionavo solo in modo geometrico e quel quarto di giro non mi piaceva... ma la formula è giusta. Prendiamo il caso generale:
Un cerchio di raggio 1/n del cerchio maggiore
R/n + R = R (n + 1)/n -->C = 2π(n+1)R/n
circonferenza cerchio piccolo CP =2πR/n
Il rapporto è proprio n + 1
Funziona
Concordo anche sulla faccia da schiaffi!!!!
Il quarto di giro di Andy torna con una posizione identica della faccia da schiaffi rispetto alla situazione originaria. E questa situazione si ripete 4 volte! Bravo ANDY!!!
Direi proprio che la mia faccia da schiaffi dia la soluzione "visiva" migliore. La curva da percorrere anticipa sempre il momento della riproduzione della faccia iniziale!
Ho provato a disegnare un cerchio di 3 cm di raggio ed uno, rotante intorno al primo e tangente ad esso, di 1 cm di raggio (grosso modo come una moneta da 10 centesimi di €). Ed in effetti, ad 1/4 di rotazione del raggio AB, corrisponde una rotazione completa della monetina. Ho cercato di estrapolare una legge generale:
se R è il raggio del cerchio fisso e R/n è il raggio del cerchio rotante, il raggio AB sarà pari a R + R/n =
= R(1+1/n) = R[(n+1)/n].
La circonferenza di centro B e raggio AB sarà pari a: 2πR[(n+1)/n] ;
la circonferenza di centro A e raggio R/n sarà pari a: 2πR(1/n) ;
il rapporto 2πR[(n+1)/n] / 2πR(1/n) sarà pari a: n+1, che indica il numero di giri che compie il cerchio rotante intorno al cerchio fisso per ritornare alla posizione iniziale, sulla base del rapporto {raggio del cerchio fisso} / {raggio del cerchio rotante};
nella fattispecie 3:1 ---> n=3, n+1=4, 4 giri della monetina per ritornare alla posizione iniziale.
Seguendo l'indicazione di Maurizio, ho provato con 2 monete da 50 centesimi, il rapporto tra i raggi come descritto prima è 1:1, n+1=2, ed in effetti i 50 cent. rotanti compiono 2 giri intorno ai 50 cent. fissi per ritornare alla posizione iniziale.
Magari ho sbagliato tutto io, Pippo e Pappo + Nobody hanno tartassato quei pochi neuroni che ho a disposizione

un 10 e lode ad ANDY !
Caro Enzo,
pensavo che la disavventura (poi a lieto fine) di Pippo e Pappo + Nobody mi avessero bollito il cervello!

no, no, ha bollito il mio!!!!!
L'importante è divertirsi
Sì, però adesso scendi da lì, se no a ogni giro ti va per quattro volte il sangue alla testa...
Va bene sacrificarsi per la scienza, ma non occorre fare il martire....
Parole sante, Enzone caro, parole sante...
Mi scuso con il Circolo, ma ogni tanto (sempre più spesso) divento un po' idiota.... vi prometto che tornerò (un po') più serio....
Comunque, ci siamo avvicinati agli epicicli e possiamo passare a rivalutare Tolomeo (almeno per quanto riguarda Terra-Luna-Sole...)
Un piccolo corollario per chi non ne ha avuto abbastanza....
Invece di avere due monete, abbiamo un anello e una moneta. La circonferenza dell'anello è tre volte quella della moneta.
Disponiamo l'anello sul piano verticale e ci mettiamo sopra la moneta (disco verde) la situazione è la medesima che conosciamo, la monetina verde, rotolando esternamente all'anello, farà quattro giri su se stessa e finirà per posizionarsi come alla partenza.
Adesso, leviamo la monetina blu e mettiamone una rossa, appesa (magneticamente) all'anello, come la vediamo nella figura.
Ovviamente la domanda è : quanti giri compirà la moneta, rotolando all'interno dell'anello, prima di riposizionarsi come si trovava all'inizio?
Infine, tolta di mezzo la monetina rossa, sdraiamo l'anello sul piano orizzontale ( lo vedete come una ellisse) poi posiamo in verticale la monetina gialla. Ora è chiaro che la monetina nel fare il giro dell'anello, (come la ruota di un trenino sul binario circolare) farà una giravolta su se stessa, come una ballerina. Ma quanti giri completi avrà fatto questa volta ?
Adesso che avete tutte le risposte la domanda per la lode. se il piano della monetina non è coincidente nè perpendicolare al piano su cui giace l'anello, cosa succede?
Scusate ma la regola ormai è che su queste cose bisogna metterci la faccia (da schiaffi)
mio piccolo contributo grafico/geometrico
https://ggbm.at/tuErteNj
secondo me la faccia da schiaffi è sempre la cosa migliore perché ti permette di vedere quando la moneta è ruotata rispetto a una direzione fissa (un po' come il periodo sinodico e quello siderale....). Vedete quanta astronomia c'è??!!!!
ok Prof, ho provveduto alla modifica. L'hai voluto tu...
caro Artù, sarebbe bello bloccarlo ogni volta che la faccia da schiaffi si ripresenti nelle stesse condizioni iniziali rispetto a un sistema fisso. Si vedrebbero bene le 4 rotazioni.... in accordo con il quarto di giro ricavato da Andy...
non so perché il testo non sia stato automaticamente convertito in link. Riprovo ora:
https://ggbm.at/thw7ZKeN
Fantastico Arturo! Proprio quello che avevo chiesto... sei veramente un mago . Ricordati che lo metteremo nella soluzione finale
Splendida dimostrazione che rende concretamente visibile tutto il meccanismo, Bravo Arturo !
Però, andando a rileggere il primissimo commento, ora che tutto è evidente a tutti, direi che anche nella affermazione di Oreste c'era una certa logica...
Mau & co..... vi pregherei di continuare con i commenti nel secondo articolo, dove ho anche riportato l'animazione di Arturo e tante altre belle facce da schiaffi!