Categorie: Fisica Fisica classica Matematica
Tags: Club dei Maghi quiz
Scritto da: Club dei Maghi
Commenti:23
Quiz: La settimana bianca di Achille e la Tartaruga
La settimana bianca di Achille e la Tartaruga
Dopo quasi 2.500 anni passati a correre di qua e di la, in tutti gli stadi del mondo alimentando le scommesse clandestine e lasciando nel dubbio milioni di appassionati, Achille e la Tartaruga decidono di prendersi una settimana di meritato riposo.
Per ossigenarsi scelgono la montagna, una bella meta sciistica di cui non divulgheremo la localizzazione per evitare che i nostri eroi vengano importunati da giornalisti e paparazzi.
La mattina del primo giorno decidono di avviarsi agli impianti di risalita per raggiungere la sommità della pista, perfettamente innevata.
Durante il percorso la tartaruga continua ad osservare il paesaggio che sfila sotto i loro occhi borbottando tra sé: “ ma guarda , guarda....chi l'avrebbe mai immaginato.....davvero perfetta....ma che forza ! “
Dopo un po' Achille, incuriosito chiede “Ma che stai dicendo? Di cosa parli?”.
La tartaruga non si sbottona più di tanto “ Niente, niente, osservavo questa pista...molto bella” poi aggiunge “Sai, Achy, visto che mi dicevi che non sei pratico di sci, potresti affittare uno slittino, tanto per cominciare a prendere confidenza con la neve, e posizionarti a metà della pista, dove il pendio è meno ripido, per scivolare verso il traguardo.”
Achille ci pensa su e risponde “ E tu dove ti metti? Di fianco a me?” E la tartaruga: “ No, io parto dalla sommità con i miei sci, mi metto nella posizione a uovo (di tartaruga) e vengo giù come una bomba. Scommetto che, partendo contemporaneamente, arrivo al traguardo insieme a te.”
Achille si mette a ridere scompostamente “ Figuriamoci se mi prendi, farò in tempo a farmi la doccia, prima che arrivi”. E aggiunge “Cosa intendi esattamente dicendo che mi devo mettere a metà della pista? Ad una altezza di metà del dislivello totale, oppure a metà della distanza tra partenza e arrivo misurata in orizzontale, oppure a metà della lunghezza della pista misurata sul manto nevoso?”
La Tartaruga non esita un istante e risponde “Sai che ti dico Achy? Mettiti pure dove ti pare, per me non fa differenza.”
Riuscirà veramente quella sbruffona a vincere la scommessa? Quale ragionamento le è frullato in testa per sfidare Achille con tanta sicurezza? Cosa c'è di così particolare nel profilo di quella pista?
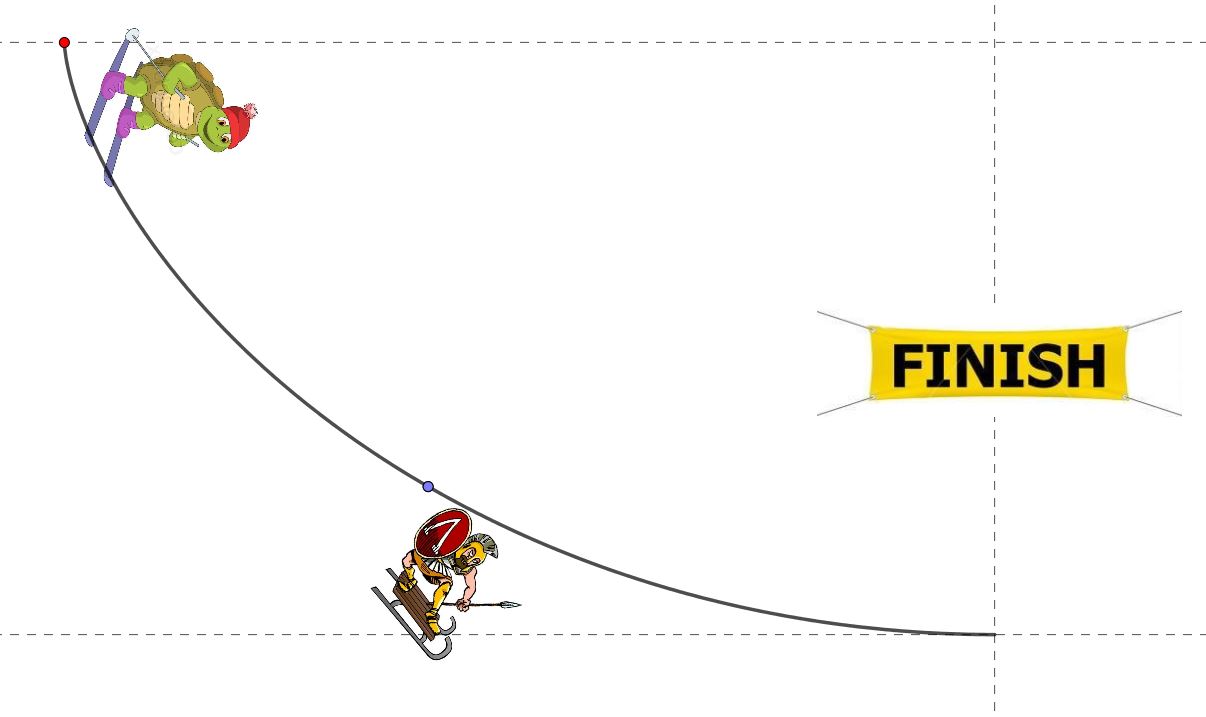
Ipotesi e suggerimenti
Il moto avviene senza dissipazione di energia: non ci sono attriti nei punti di contatto con la pista, l'impatto dell'aria non è da considerare (come se il moto avvenisse nel vuoto), i concorrenti vanno considerati come corpi rigidi (privi di movimenti interni, non possono neppure tossire) , non c'è alcun rotolamento ma solo scivolamento (strisciamento senza attrito).
Come origine del sistema di riferimento conviene impostare il punto del traguardo, nella parte più bassa della pista.
Alla fine della pista, oltre il traguardo, il profilo della superficie prosegue in salita con una simmetria speculare
QUI la soluzione del quiz
QUI tutti i quiz dei Maghi
QUI tutti i quiz del blog
QUI altri percorsi da calcolare!
23 commenti
Se fosse una curva di equazione y = 1 - [(1 - x^2)]^(½), per intenderci un semicerchio di raggio unitario con concavità rivolta verso l'alto e tangente nel punto del traguardo
(origine degli assi [0, 0], coordinate del centro [0, 1]),
il punto Tartaruga e il punto Achille si troverebbero su un arco di tale cerchio e alla stessa distanza (pari al raggio) dal centro del cerchio, simulando un movimento oscillatorio vincolato, come in un pendolo dove il filo è lungo quanto il raggio, disegnando un arco di cerchio durante una oscillazione.
Nel caso del pendolo, il filo rappresenta il vincolo del movimento oscillatorio;
qui, per le condizioni enunciate nel quiz, il vincolo è rappresentato solo dal "filo di rasoio" della curva stessa.
Ora, siccome il periodo di oscillazione di un pendolo è pari a:
T = 2π [(L / g)]^(½)
e dipende quindi solo dalla lunghezza del filo (essendo g e π costanti), il tempo per raggiungere il traguardo sarà pari a mezzo periodo:
T = π [(L / g)]^(½), uguale sia per la Tartaruga che per Achille (in questo caso L è pari al raggio unitario), e, come nel pendolo, non dovrebbero dipendere le masse relative della Tartaruga e di Achille.
Entrambi sono sottoposti alla stessa accelerazione gravitazionale rivolta verso il centro di massa della Terra, ma la Tartaruga si trova ad una quota, rispetto al piano di terra (la retta tangente alla curva nell'origine), superiore alla quota di quella di Achille, e quindi dotata di una maggior quantità di energia potenziale che si trasforma in maggior energia cinetica durante il moto, rispetto ad Achille (la Tartaruga deve compiere un percorso più lungo di Achille nella stessa quantità di tempo: deve "correre/scivolare" più velocemente).
Sempre che si tratti di questa particolare curva
Ci provò anche Galileo ma non centrò la soluzione. eh eh eh
Ci vuole una intera notte di lavoro per risolvere il problema.
Il problema è stato perfettamente inquadrato da Andy , ma la soluzione non è data da un profilo ad arco di cerchio. Il paragone con il pendolo è una buona idea ma le oscillazioni di un pendolo hanno periodi diversi se la loro ampiezza è diversa. Solo entro i limiti di un arco molto piccolo ( mezzo decimo di radiante) i punti di partenza sono praticamente ininfluenti e i periodi sono (quasi) uguali.
In altri termini, nel caso del profilo circolare ( tipo pendolo) solo se la differenza tra i punti di partenza dei due concorrenti è molto piccola i due tempi saranno molto vicini, seppure non uguali, ma nel nostro caso questa differenza può essere qualsiasi, anche molto grande, e il tempo sarà sempre lo stesso.
In realtà, come dice Leandro, anche Galileo pensò ad un cerchio, quindi c'è di che essere soddisfatti della compagnia.
Comunque la notte è passata... quindi?
Non basta una notte, c vuole anche l'artiglio del leone.
Sì, Leandro, hai ragione è un bel problemino.
Sembra che per l'ultima nevicata, il pendio si sia ulteriormente innevato, cambiando completamente forma... Uno degli addetti è perfino rotolato fino in fondo...
Caro Oreste,
parole sacrosante le tue circa i tempi di oscillazione di un pendolo relativi ad angoli di oscillazione non superiori ad un determinato (e piccolo) intervallo.
Ciò che hai scritto più l'intervento "tra le righe" del grande Enzo mi hanno dato degli ottimi input:
sapete che faccio? Cambio pendio, anzi no, cambio curva!
Allego dei disegnini (sono più rapido scrivere a mano che non a tastiera!)
1) https://i.imgur.com/ZJsvvKQ.jpg
2) https://i.imgur.com/Rk8MdXM.jpg
3) https://i.imgur.com/Thx6rIr.jpg
Eh eh per conquistare la bella Elena ci vuole una guerra...
Eh già Leandro,
come per dimostrare la convergenza ad un valore di una serie divergente come nel tuo avatar,
ci volle il geniale matematico indiano Srinivasa Ramanujan (che poi più che una convergenza è una distribuzione media di valori oscillante rispetto ad un valore di riferimento)
Assolutamente in tema, Leandro, il commento sulla bella Elena (e sulla guerra).
Achille dovrebbe saperlo bene...proprio lui.
Andy, il profilo non è quello di una parabola. La velocità va calcolata lungo la traiettoria, sulla coordinata curvilinea del profilo cercato.
Direi che nel cercare la soluzione si può procedere in due modi.
Avanzare una ipotesi sul tipo di curva, ragionando sulle sue caratteristiche geometriche, come la specularità rispetto all'asse verticale (vedi cerchio o parabola) e verificando poi che il moto che si manifesta sulla curva ipotizzata abbia le caratteristiche dinamiche osservate.
Oppure costruire la risposta considerando le caratteristiche dinamiche del moto che si osserva sulla curva sconosciuta e, dalla sua equazione dinamica risalire alla equazione geometrica della funzione (non necessariamente in forma cartesiana, ma ad esempio in forma parametrica). Poi si tratterà di inventare un nome per questa funzione o di riconoscerla tra quelle che un nome già ce l'hanno.
Sappiamo che, nel caso di Achille e la Tartaruga, il moto è periodico, ma non è solo periodico, è un moto che prescinde dalla ampiezza della oscillazione. Ha un nome particolare, questo moto. E' lo stesso moto che si ottiene in un sistema costituito da una molla e da un peso. Spostando il peso dalla posizione di equilibrio la molla si tende e si comprime alternativamente producendo una oscillazione periodica e ..... quell'altra parola.
Ciao Maurizio,
dovrebbe trattarsi di un moto armonico, come il moto della proiezione di un punto di una circonferenza su un proprio diametro fisso.
Se i due punti partissero con le proprie altezze da due curve come quella in figura, perfettamente uguali e parallele, uno su una curva, l'altro sull'altra curva, passerebbero nello stesso istante dal punto di minimo, per collocarsi alla stessa altezza ma dall'altra parte rispetto all'asse di simmetria della curva e continuare all'infinito, dato che è stato ipotizzato nullo il contributo di qualsiasi attrito, nessuna dissipazione di energia, nessun movimento "intrinseco" dei corpi scivolanti, considerati perfettamente rigidi.
Intuisco che sia applicabile il principio della conservazione dell'energia, con trasformazione istante per istante della quantità di energia potenziale in energia cinetica dei due corpi e viceversa, dopo il passaggio dal punto di minimo della curva.
Tradurre matematicamente tutta 'sta pappardella è un'altra storia.
Come diceva Obi Wan Kenobi.... Usa la forza , Andy....
Andy non dire niente a nessuno... ssshhh....
Invece di lasciare libero il filo del pendolo, fai in modo che il filo tracci l'evolvente di qualcosa che già conosci bene...
Io non ho detto niente... Il mio orologio a pendolo funziona così....
Che mal di denti con questi evolventi!
Vabbè, visto che se ne è parlato tanto in questi ultimi giorni di monete che rotolano, epicicli, cicloidi e deltoidi vari, son giunto alla conclusione che la figura rappresentata nel quiz non è né parabola né semicerchio, bensì mezza cicloide a pancia all'aria.
E siccome i due punti Tartaruga e Achille scivolano in modo armonico in condizioni ideali (assenze di attrito varie, dissipazione di energia nulla) lunga tale curva, mi riaggancio al pendolo (senza appendermi):
nel pendolo, il tempo necessario per raggiungere il punto di minimo è T = π [(L / g)]^(½) valido solo per piccole oscillazioni; bene, e se nell'equazione sostituisco la lunghezza del pendolo con il raggio r del cerchio generatore della cicloide T = π [(r / g)]^(½), annullo la dipendenza del tempo di oscillazione dalla lunghezza del filo a dai piccoli angoli di oscillazione ed essendo ugual costante la misura del raggio r, da qualunque posizione si scivoli, il tempo necessario a raggiungere il punto di minimo sarà sempre T = π [(r / g)]^(½).
Sempre in buona compagnia, Andy. Leggi un po' qui...
Nella notte del 23 novembre 1654 dalle ore 10.30 alle ore 12.30 Pascal ebbe un'estasi mistica che lo indusse ad abbandonare la scienza e la matematica per dedicarsi alla teologia .
Ma una notte del 1658 un terribile mal di denti gli impediva di dormire e per distrarsi e dimenticare il dolore rivolse di nuovo la sua attenzione allo studio della cicloide : miracolosamente il dolore cessò e questo fu interpretato da Pascal come un segno del Cielo che dovesse continuare ad interessarsi alla matematica.
Immaginiamo di disegnare due cerchi e la cicloide (che ipotizzi sia la curva misteriosa).
Prima disegniamo il cerchio generatore della cicloide, di raggio L . Direi di disegnarlo con il centro sull'asse y, al disopra del punto origine ( il traguardo)
Poi tracciamo un cerchio di raggio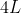
, sempre con il centro sull'asse y di sopra della posizione del traguardo.
Infine abbiamo la cicloide con la concavità verso l'alto, posizionata simmetricamente rispetto l'asse verticale, quindi con il punto più basso coincidente con l'origine.
Il pendolo di lunghezza L che descrivi nel tuo commento, che per piccole oscillazioni ha periodo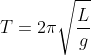
, ha il punto di sospensione nel centro del cerchio piccolo. Un quarto di questo periodo è il tempo per coprire la distanza dalla posizione superiore al punto di minimo e vale quindi 
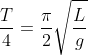La traiettoria è un arco (piccolo) di cerchio.
Pensiamo ad un secondo pendolo con punto di sospensione nel centro del cerchio grande. La lunghezza del pendolo sarà il raggio di questo cerchio, e varrà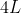
. Di conseguenza, sempre e solo per piccole oscillazioni, il suo periodo sarà 
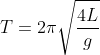e il quarto di periodo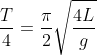 
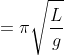
La distanza da quest'ultimo centro alla cicloide varia da un valore minimo di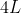
(considerando la distanza dall'origine, il punto di arrivo, in verticale) ad un massimo che corrisponde alla distanza tra il centro di sospensione e il punto di partenza fissato sulla cicloide. Per fare percorrere al peso del pendolo una traiettoria che non segua un arco di cerchio ( raggio fisso) ma un arco di cicloide ( raggio variabile), occorrerebbe, come nell'orologio di Enzo, interferire nel movimento del filo del pendolo con "adeguati" profili . In tal modo il periodo sarà sempre uguale per piccole o grandi oscillazioni.
Ma quale sarà questo periodo? E' davvero deducibile da quello di un pendolo con lunghezza costante?
Come si diceva, è possibile fare l'ipotesi che la curva sia una tra quelle note. In questo caso ne conosceremo l'equazione e potremo fare delle verifiche. Però potremmo anche non trovare, a tentativi, la curva giusta.
Allora possiamo procedere in altro modo, dimentichiamoci delle curve che conosciamo, cerchiamo di costruire una relazione tra posizione e velocità e accelerazione che rappresenti il moto (generato da una o più forze) e da questa relazione risaliamo alla equazione della traiettoria. Solo alla fine, osservando questa equazione, potremo dire se la riconosciamo o meno e se sappiamo quale nome le sia stato attribuito (da Galileo).
Comunque il quiz non chiede di calcolare quale sia il valore del tempo di discesa, o la sua espressione matematica, ma chiede quale sia la curva per la quale , indipendentemente dalla posizione di partenza, il tempo di discesa sia sempre lo stesso.
Vai, che vai bene... in ogni caso, per male che vada, c'è sempre la Teologia
Quella curva arcuata, sono piu’ di cinquant’ anni che mi venne in mente il descriverla, e l’ammirai per una curvita’ graziosissima per adattarla agli archi di un ponte.
G.Galilei
Probabilmente, per calcolare le equazioni del moto dei due, bisogna tener conto della conservazione dell'energia meccanica come insieme di energia potenziale ed energia cinetica, della forza di richiamo esercitata dall'azione della accelerazione gravitazionale sui due corpi armonizzata dal particolare profilo della curva, delle componenti radiali e trasversali di accelerazione e velocità dei due durante il moto acciocché si possa poi ricavare l'equazione di tale curva, meglio in forma parametrica che cartesiana perché più complessa.
Ma io mi fermo qui perché le mie (poche) conoscenze di matematica e fisica si fermano alla maturità scientifica conseguita poco più di tre decadi fa e su tali conoscenze prevalgono di più i ricordi sbiaditi che non quelli netti.
Però la curva è una cicloide, isocrona, tautocrona e sinanco brachistocrona in un campo di gravità:
perché lo disse Huyghens, e di lui mi fido.
Penso prenderò un breve pausa per dedicarmi non alla teologia, bensì alla teosofia
Mentre l'amico Andy rispolvera e tira a lucido i ricordi di scuola (una faccenda domestica che riguarda quasi tutti) abbiamo deciso di lasciare un paio di giorni di tempo ad altri volenterosi che desiderino aggiungere i loro commenti .
In assenza di nuovi interventi procederemo a pubblicare la nostra soluzione.
....che si tratti forse della brachistocrona?
Si tratta proprio di una brachistocrona!
C'è un interessantissimo video al riguardo, ma attendo la soluzione del quiz per proporlo in modo da non rovinare la sorpresa ;)
Caro Pievani, vedremo con piacere il video e ti ringraziamo per attendere la soluzione che verrà data.
La brachistocrona è il cammino più veloce per andare da un punto A ad un punto B sottostante e non allineato. La curva che descrive tale cammino ha però una ulteriore caratteristica, quella su cui è focalizzato questo quiz, ossia la identità dei tempi necessari a raggiungere il punto B partendo da punti sovrastanti A e A' comunque diversi tra loro.
E questa caratteristica conferisce alla curva il nome di .... (puntini , puntini)