Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"

Tutti dovrebbero ricordare le formule che ci regalano le aree e i volumi delle forme geometriche più comuni. Ma, probabilmente, non tutti sanno come e chi è riuscito a ricavarli. In realtà, oggi vi sono metodi matematici estremamente efficaci, ma come la mettiamo per gli antichi? Eppure, anche senza integrali, derivate, trigonometria, limiti, algebra, ecc., ecc., erano già riusciti a determinarne i valori attraverso incastri geometrici di rara genialità e, soprattutto, eleganza. In particolare merita un posto d’onore il grande Archimede, l’uomo della “sfera e del cilindro”, colui che usava la leva per calcolare aree, volumi e centri di gravità.

Il metodo meccanico

Nel corso di matematica (QUI) abbiamo già trattato i metodi che gli avevano permesso di arrivare a un valore approssimato del pi greco e alla determinazione dell’area del cerchio. A quest’ultimo riguardo vale la pena ricordare il suo fantastico enunciato: “L’area di un cerchio è equivalente a quella di un triangolo rettangolo che abbia per cateti il raggio e la circonferenza”.

Tuttavia, è bene non dimenticare mai che a quei tempi non esisteva ancora l’algebra (né tantomeno gli integrali) e che le sue deduzioni erano basate prevalentemente sull’empirismo e su una eventuale ricerca posteriore di una conferma geometrica, spesso data in modo “moderno” da scienziati e studiosi nei secoli successivi. Il suo “metodo” è ben sintetizzato da lui stesso:

“… alcune cose si manifestarono prima per via meccanica, e poi le dimostrai geometricamente; perché la ricerca fatta con questo metodo non importa una vera dimostrazione. Però è certamente più facile, dopo avere con tal metodo acquistato una certa cognizione delle questioni, trovarne la dimostrazione, anziché cercarla senza averne alcuna cognizione preliminare.”

Per determinare le caratteristiche di una figura di cui non si conosce l’area, il volume o la posizione del baricentro, Archimede usa una o più figure di cui si conoscono previamente queste caratteristiche. Archimede immagina che queste figure siano sezionate da un piano, in tal modo che una superficie sia ridotta ad un segmento oppure un solido sia ridotto ad una superficie. Partendo da osservazioni esclusivamente geometriche sulle figure considerate, Archimede determina proporzioni tra segmenti oppure tra segmenti ed aree. Si attribuiscono ai segmenti e alle aree, pesi distribuiti in modo uniforme. In particolare, il peso di un segmento lineare è proporzionale alla sua lunghezza, il peso di una figura piana è proporzionale alla sua area, mentre il peso di un solido è proporzionale al suo volume. Archimede introduce la leva e cerca gli equilibri delle varie figure. I risultati nascono, quindi, attraverso equivalenze misurate direttamente.

Raggiunto lo scopo, la dimostrazione pratica cessa di essere fondamentale e diventa solo “un di più”. Tuttavia, solo attraverso le sue equivalenze tra figure è stato possibile trovare metodi basati su nozioni allora sconosciute. In qualche modo, le dimostrazioni che noi daremo non sono realmente di Archimede, ma sono state trovate solo e soltanto basandosi sulle sue geniali deduzioni.

Il caso della sfera e delle sue relazioni con il cilindro è uno dei più illuminanti e vale la pena affrontarlo con particolare attenzione. Seguiremo i metodi che meglio si avvicinano alle conclusioni estremamente complesse ottenute dal grande siracusano. Ricordiamo che lui stesso fu molto fiero dell’ostacolo enorme che aveva superato e che chiese espressamente di porre una scultura con una sfera e un cilindro vicino alla sua tomba.

Tomba che sembra essere stata individuata, anche se delle figure geometriche non è rimasto alcun segno. E’ interessante, a questo riguardo, richiamare le parole di Cicerone nelle sue Discussioni Tusculane:

“… dalla stessa città (Siracusa) risveglierò dalla polvere [...] un piccolo uomo umile che visse molti anni dopo, Archimede. Quando ero questore scopersi il suo sepolcro, tutto circondato e rivestito di rovi e di pruni, di cui i Siracusani ignoravano l’esistenza, anzi escludevano che ci fosse. Ricordavo alcuni versi di poco conto, che sapevo trovarsi iscritti sulla sua tomba: dicevano che sulla sommità del sepolcro era posta una sfera con un cilindro. Un giorno scrutavo ogni angolo con lo sguardo (fuori della parta sacra a Ciane c’è un gran numero di sepolcri) e scorsi una colonnetta che non sporgeva molto dai cespugli, su cui stava l’effigie di una sfera e di un cilindro. Subito dissi ai Siracusani (si trovavano con me i più ragguardevoli cittadini) che pensavo si trattasse proprio di ciò che cercavo. Si mandò molta gente con falci e il luogo fu ripulito e sgombrato. Quando fu aperto l’accesso, ci avvicinammo al lato frontale del piedestallo: si vedeva un’iscrizione quasi dimezzata, in cui i versi erano corrosi verso la fine di ciascuno. Così una delle più celebri città della Magna Grecia, e una volta anche fra le più dotte, avrebbe ignorato l’esistenza della tomba del suo più geniale cittadino se non gliela avesse fatta conoscere un uomo di Arpino”.

Bene, partiamo dalla superficie sferica, attraverso uno svolgimento di una semplicità e di una eleganza disarmante, da lui stesso ispirato. La deduzione della superficie di una sfera è stata una delle imprese che più lo ha esaltato, soprattutto per i due enunciati che ne seguirono: “La superficie di una sfera equivale alla superficie di quattro cerchi di uguale raggio” e “La superficie di una sfera equivale alla superficie laterale di un cilindro che abbia come base la circonferenza di raggio uguale a quello della sfera e come altezza il diametro”. Non stupiamoci, perciò, di cominciare calcolando le superfici di altre figure geometriche: cono, tronco di cono e cilindro.

La superficie laterale di un cono retto

Consideriamo un cono retto di vertice A che abbia per base un cerchio di raggio r (Fig. 1).

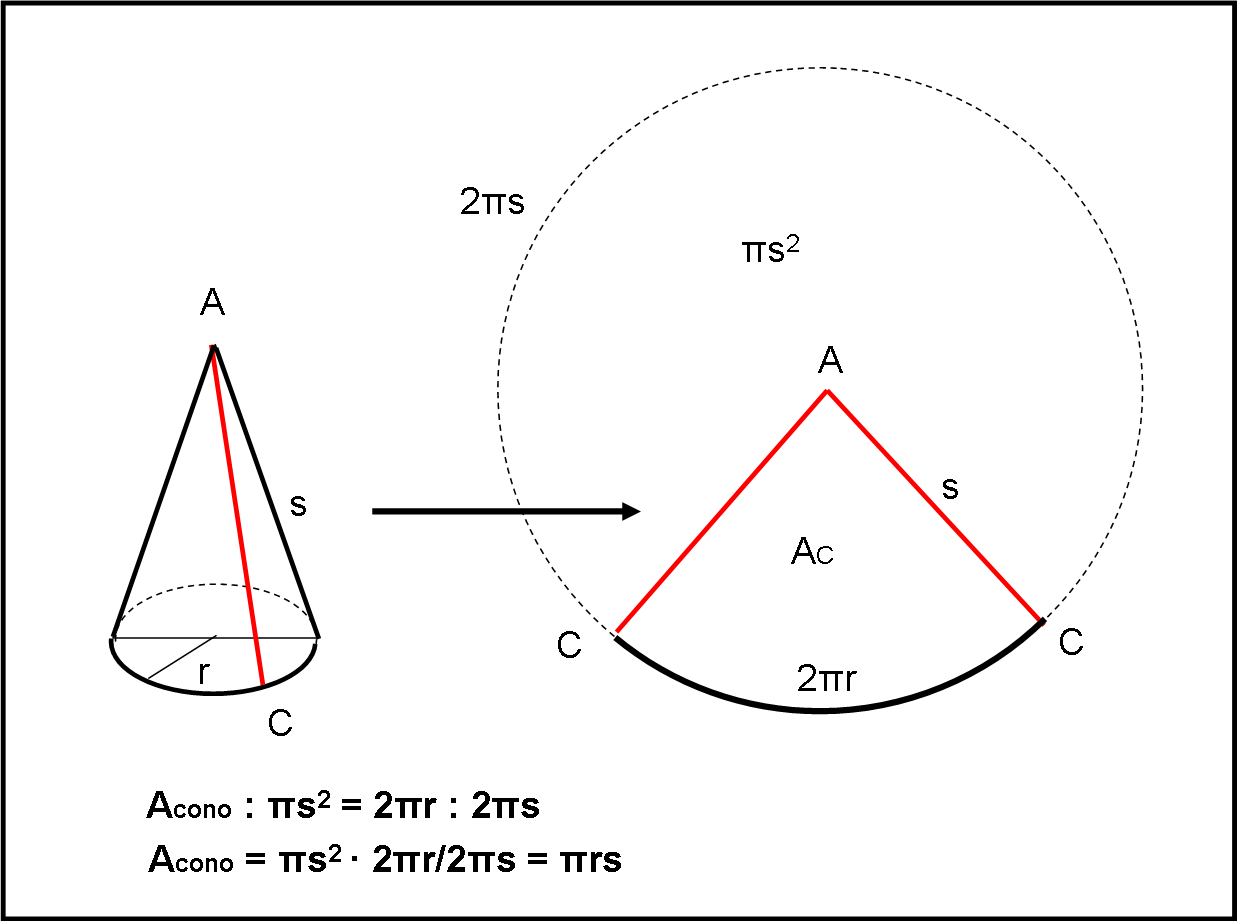
Qualsiasi piano passante per il vertice A e perpendicolare al cerchio di base, individua il lato (apotema) AC del cono e chiamiamolo s. Ritagliamo il cono lungo AC (può essere qualsiasi) e apriamo la figura che diventa piana. Ciò che risulta è un settore circolare di un cerchio di raggio s, il cui arco è pari alla circonferenza di base del cono di partenza. Basta solo imporre una semplice proporzione:

l’area del settore circolare (il cono di partenza) sta all’area dell’intero cerchio di raggio s, come l’arco del settore sta all’intera circonferenza di raggio s. In parole matematiche:

A_cono : πs² = 2πr : 2πs

A_cono  = πs²·2πr/2πs = πrs           …. (1)

Ovviamente, abbiamo considerato solo l’area della superficie laterale, escludendo quella del cerchio di base.

La superficie laterale di un cilindro retto

I cerchi di base abbiano nuovamente come raggio r e h sia l’altezza del cilindro (Fig. 2).

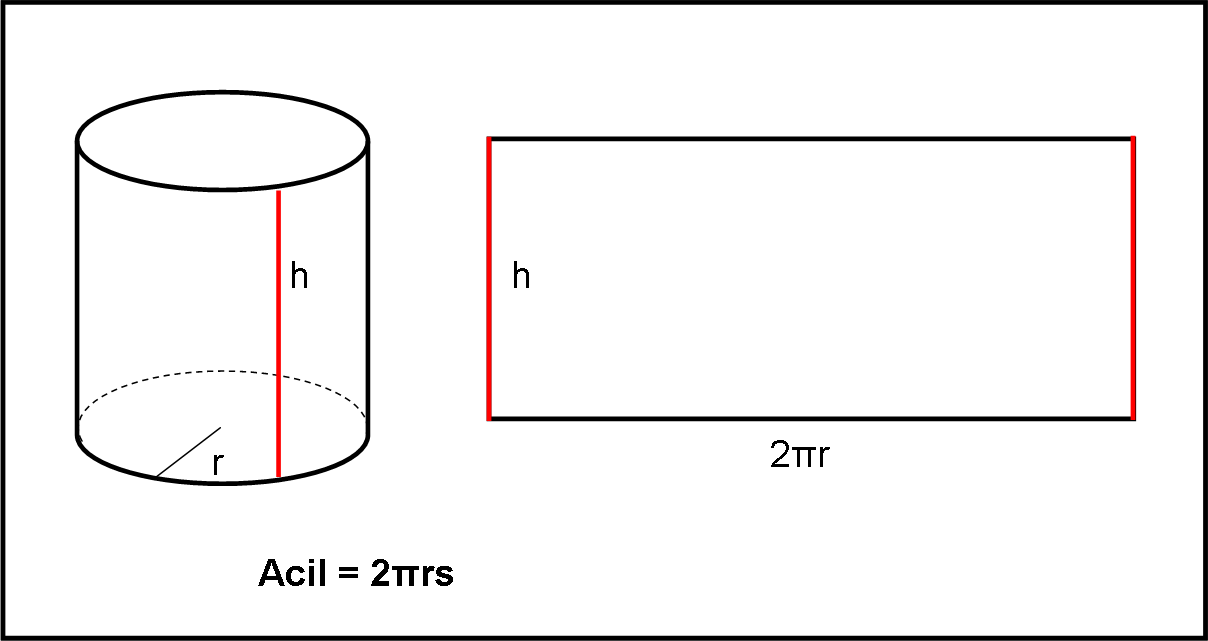
Ritagliamo il cilindro lungo una linea perpendicolare al cerchio di base e apriamo la figura. Essa diventa un rettangolo che ha come base la circonferenza di base del cilindro e come altezza h. Si ha subito:

A_cil = 2πrh            …. (2)

A titolo di curiosità (si fa per dire) possiamo concludere che la superficie laterale di un cono retto è la metà di quella di un cilindro retto di uguale base, che abbia come altezza il lato del cono.

La superficie laterale di un tronco di cono

Conoscendo l’area della superficie laterale di un cono retto, bastano pochi semplici calcoli per determinare l’area della superficie laterale di un tronco di cono retto. Facciamoci aiutare dalla Fig. 3.

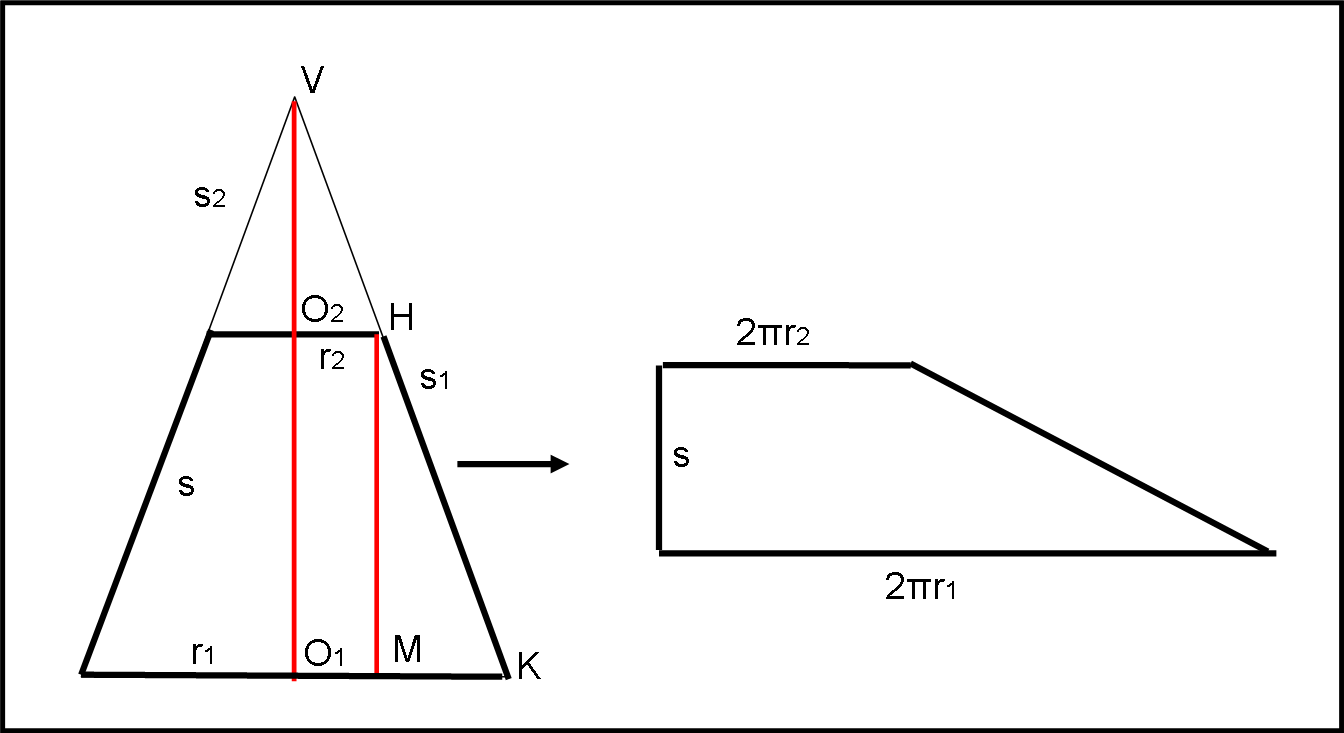
Si parte da un cono di lato (apotema) s₁ e cerchio di base di raggio r₁. Si taglia poi questo cono con un piano perpendicolare all’altezza del cono e si ottiene un cono più piccolo di apotema s₂ e raggio di base r₂.

Segue immediatamente che la superficie del tronco di cono è data dalla differenza tra la superficie del cono più grande meno quella del cono più piccolo.

Da quanto sappiamo sulla superficie laterale di un cono retto, possiamo scrivere:

A_tr.cono = πr₁s₁ - πr₂s₂         …. (3)

Sappiamo anche che s (apotema del tronco di cono) vale:

s = s₁ – s₂

s₁ = s + s₂

inseriamo s₁ nella (3)

A_tr.cono = πr₁(s + s₂) - πr₂s₂

A_tr.cono = πr₁s + πr₁s₂ - πr₂s₂

A_tr.cono = πr₁s + πs₂ (r₁ - r₂)             …. (4)

La Fig. 3  ci mostra anche che i triangoli VO₂H e HMK sono simili, per cui vale:

s₂/r₂ = s/(r₁ – r₂)

s₂ =  r₂s/(r₁ – r₂)

Inseriamo s₂ nella (4) e otteniamo:

A_tr.cono = πr₁s + πr₂s (r₁ - r₂)/(r₁ – r₂)

A_tr.cono = πs(r₁+ r₂)              …. (5)

Il che vuol dire che l’area della superficie laterale di un tronco di cono è equivalente a quella di un trapezio avente come basi le due circonferenze di base e per altezza l’apotema s.

Due tronchi di cono, due coni e una ... sfera

La Fig. 4 ci permette di costruire una figura geometrica molto interessante.

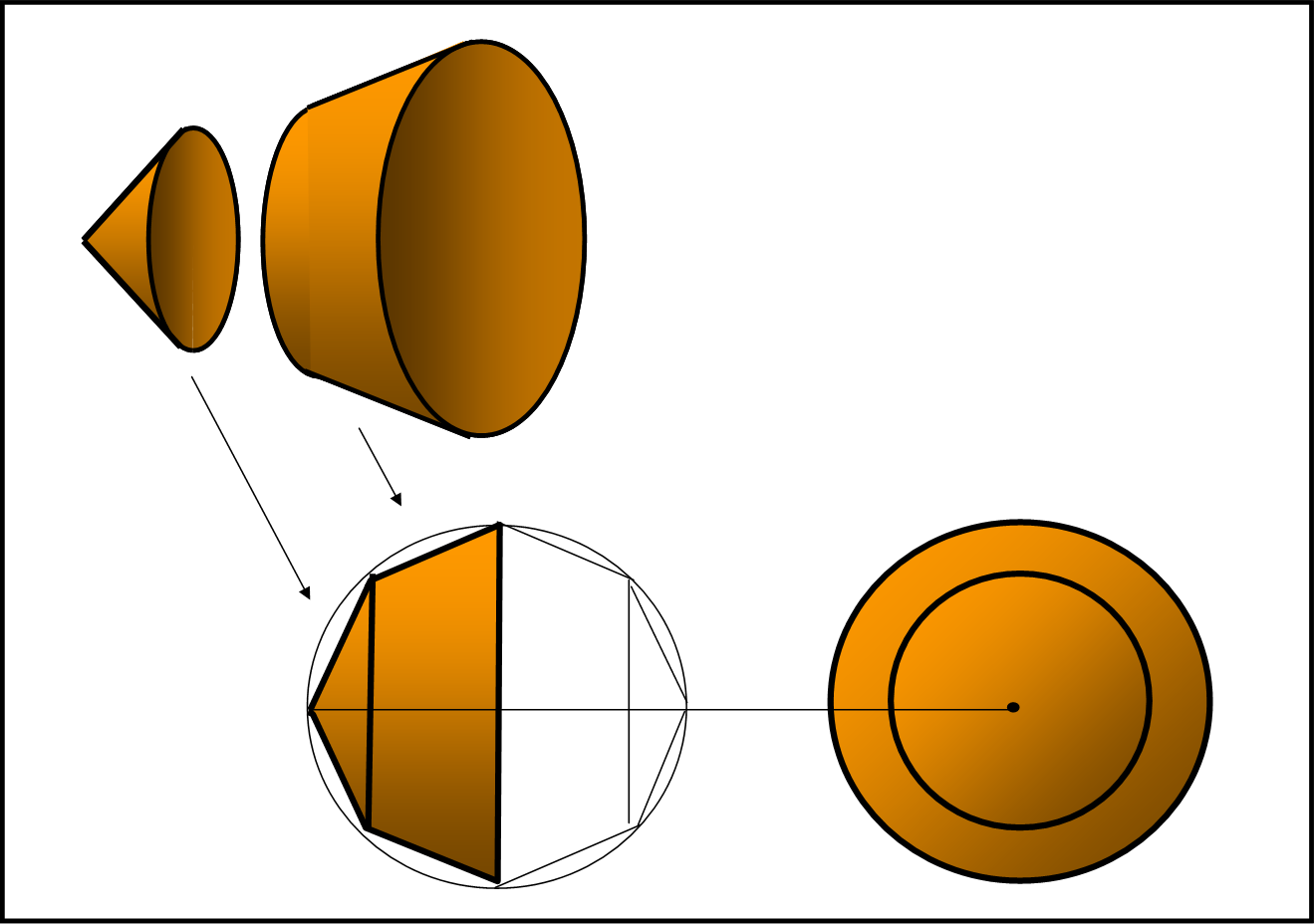
Giocando correttamente con le dimensioni, si considerano un tronco di cono (senza le basi) e un cono (anch’esso senza la base) in modo che il cerchio piccolo del tronco sia uguale a quello del cono. Le dimensioni delle due figure sono tali che la loro unione può essere iscritta in una sfera (parte bassa a sinistra). La vista frontale si ha in basso a destra. Basta raddoppiare la figura così costruita e inserirla nell’altra semisfera. Vista di taglio risulta chiaro che la sezione della figura è un ottagono regolare e proprio su questa sezione noi andiamo a lavorare.

Notiamo che avremmo ottenuto lo stesso risultato prendendo un ottagono regolare e facendolo ruotare attorno al diametro orizzontale della sfera in cui è iscritto. Notiamo anche che l’utilizzo di due tronchi di cono e di due cilindri è un’approssimazione semplicistica, dato che avremmo potuto avvicinarci sempre più alla sfera aumentando il numero dei tronchi di cono e ridurre a dimensioni irrisorie i due coni. Un metodo che ci mostrerebbe un chiaro passaggio al limite o addirittura un integrale. Noi vogliamo invece dimostrare che il risultato finale si può ottenere giocando semplicemente con il nostro ottagono e con pochi triangoli simili.

Passiamo, perciò, alla Fig. 5, dove il nostro ottagono è di vertici ABCDEFGH e il cento del cerchio circoscritto è O.

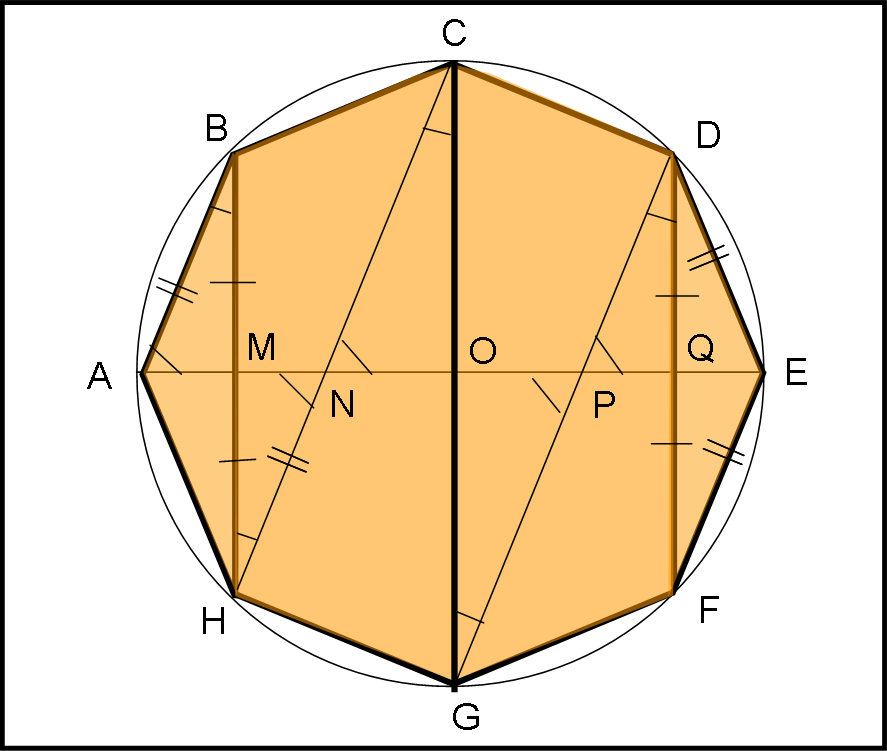
Tracciamo qualche linea e segniamo qualche angolo. Le ovvie simmetrie che esistono in una figura così regolare ci permettono di dedurre con gran facilità che i triangoli rettangoli ABM, MHN, PDQ, QDE sono tutti uguali tra loro. Chiamiamo d i segmenti AM = MN = PQ = QE.

Risulta anche immediato il fatto che il triangolo HMN è simile al triangolo NCO e che quest’ultimo è uguale a OGP. L’importante è poter dire che i segmenti ON e OP sono uguali e li poniamo uguali a d’.

Utilizziamo, adesso, la Fig. 6 che evidenzia meglio i triangoli che ci interessano (verdi e azzurro) e i loro lati. Dalle uguaglianze e dalle similitudini notate precedentemente possiamo scrivere che il rapporto dei loro cateti è costante.

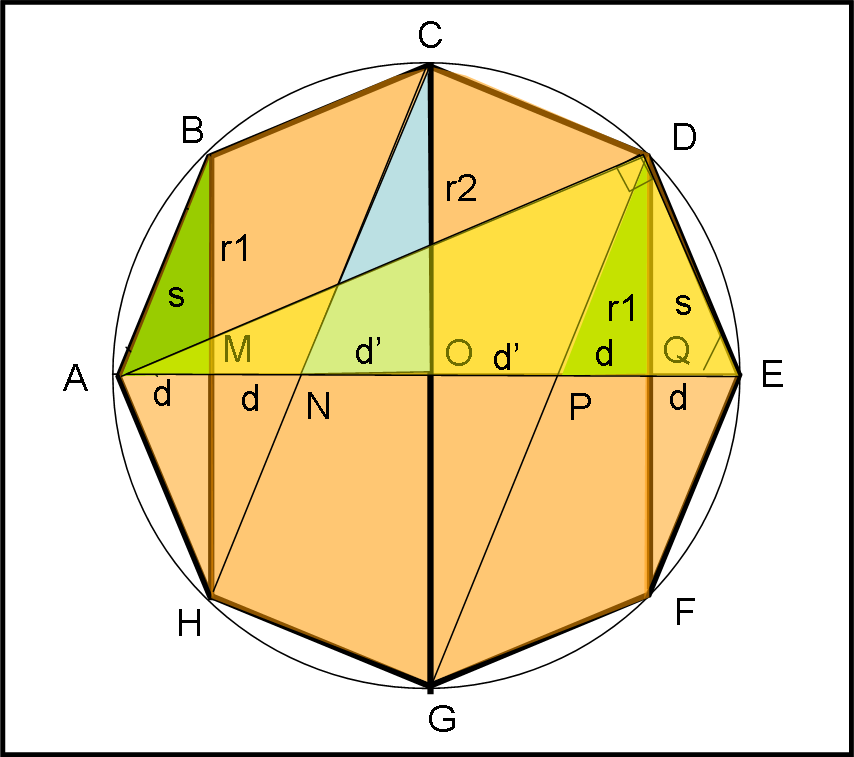
r₁/d = r₂/d’ = r₁/d  = cost.             …. (6)

L’ideale sarebbe collegare la costante ad altre lunghezze più “significative”. La faccenda è semplicissima, considerando il triangolo giallo ADE. Esso ha per lato il diametro della sfera circoscritta e quindi l’angolo alla circonferenza ADE è un angolo retto. Inoltre l’angolo QED è in comune con quello del triangolo QED. Ne segue che i triangoli ADE e QED sono simili, per cui vale la relazione:

r₁/d = s/AD

Ma dalla (6), possiamo scrivere:

r₁/d = r₂/d’ = r₁/d  = s/AD

o, ancora:

r₁/d = s/AD

r₂/d’= s/AD

r₁/d  = s/AD

sr₁ = AD d

sr₂ = AD d’

sr₁ = AD d

sommiamo le tre relazioni:

sr₁ + sr₂ + sr₁ = AD d + AD d’ + AD d

r₁ + r₂ + r₁ = AD(d + d’ + d)/s                    …. (7)

Guardando la Fig. 6 si ricava subito che

d + d + d’ = AE/2

Sostituendo nella  (7) si ha:

r₁ + r₂ + r₁ = AD·AE/2s        …. (8)

Teniamoci “calda” questa formula  e passiamo a calcolare le aree delle superfici esterne dei tronchi di cono e dei coni che ci sono serviti a costruire la figura geometrica precedente (vedi Fig. 4), utilizzando la sezione di Fig. 7

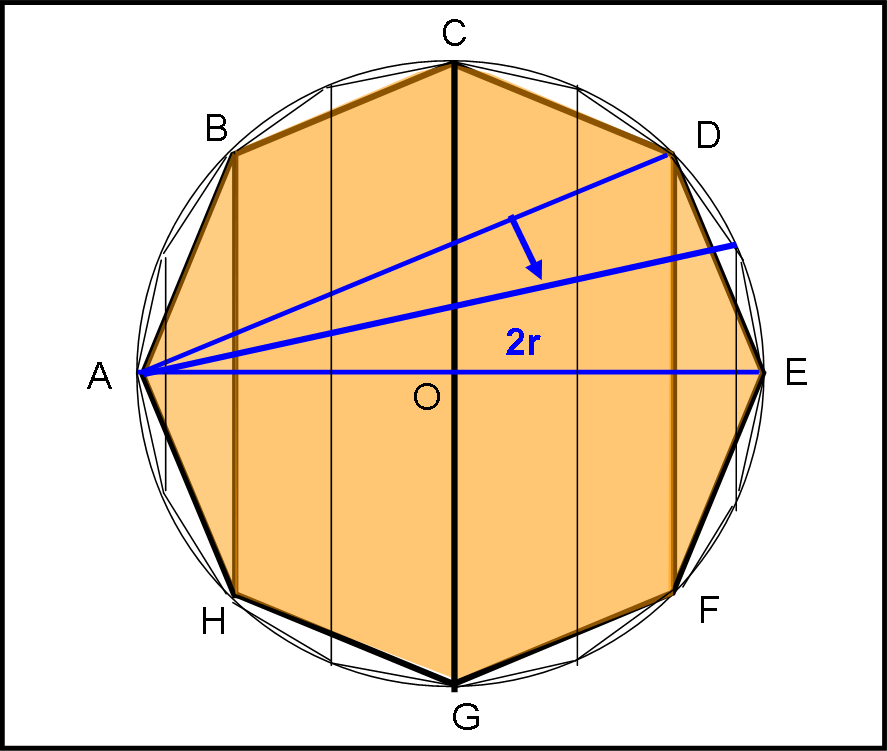
A_{cono ABH} = πr₁s = A_{cono DEF}

A_{tr.cono BCGH}  = π (r₁ + r₂)s = A_{tr.cono CDFG}

L’area totale A_tot è data da:

A_tot = 2πr₁s + 2π(r₁ + r₂)s = 2πs(r₁ + r₂ + r₁)

Ricordando la (8):

A_tot = 2 πs AD·AE/2s

A_tot = π AE·AD = 2πr·AD

Come abbiamo già accennato, la stessa identica formula l’avremmo potuta ottenere aumentando il numero di lati della sezione ottagonale, ossia aumentando il numero di tronchi di cono e diminuendo le dimensioni dei due coni finali. L’unica cosa che sarebbe cambiata sarebbe stato il segmento AD (la congiungente il vertice del cono sinistro con il bordo del cono destro). Tutto il resto della trattazione sarebbe stata solo più lunga, con molti più triangoli simili, ma sempre con l’angolo ADE retto, dato che continua a insistere su mezza circonferenza.

Aumentando, quindi, il numero di poligoni si arriverebbe a far coincidere AD con AE. Ma AE è proprio il doppio del raggio e, quindi, la formula finale della superficie sferica diventa:

A_sfera = 2πr2r

A_sfera = 4πr²               …. (9)

Probabilmente, Archimede aveva già considerato un numero molto più alto di poligoni, ma il succo del discorso non cambia. Mamma mia! Che genio e che eleganza …

Tuttavia, la faccenda ha dei risvolti ancora più generali e esaltanti per il genio siracusano.

Ricordiamo quanto vale l’area della superficie laterale di un cilindro:

A_cil = 2πrh

Se prendiamo come altezza del cilindro il diametro del cerchio di base, otteniamo:

A_cil = 4πr²

Si può concludere che l’area di una superficie sferica di raggio r è del tutto equivalente a quella della superficie laterale di un cilindro che ha la base con lo stesso raggio e l’altezza uguale al diametro. In poche parole vale la Fig. 8.

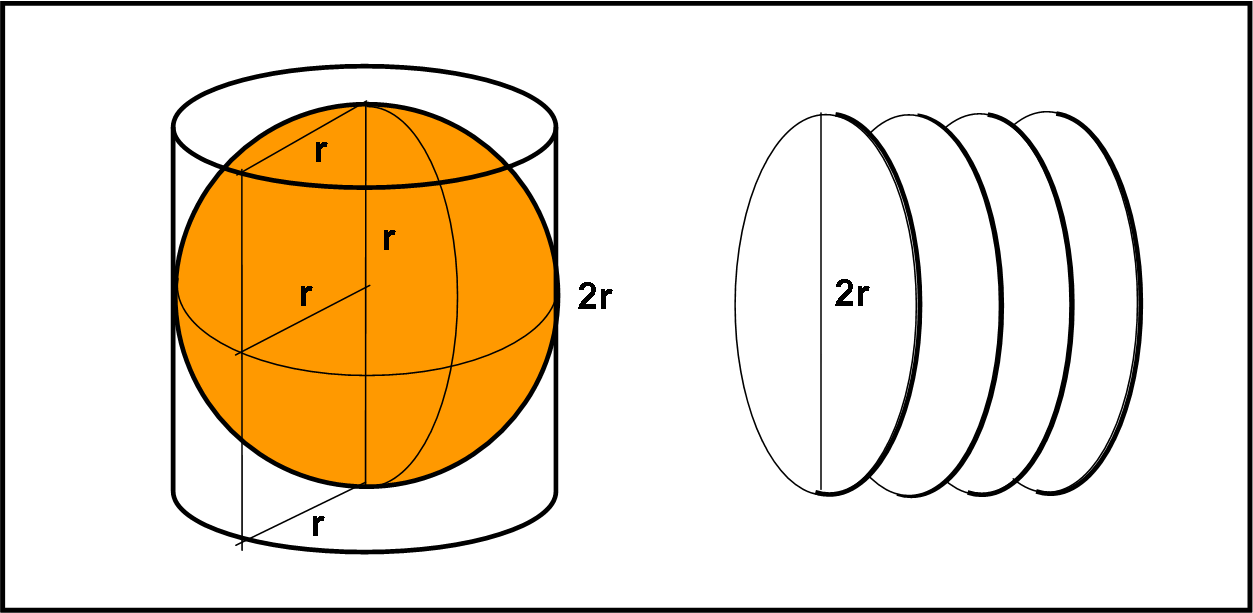
Ma non basta…

Quanto vale l’area di un cerchio di raggio r?

A_cer = πr²

Il che vuol dire che l’area della superficie di una sfera equivale all’area di quattro cerchi massimi della stessa sfera.

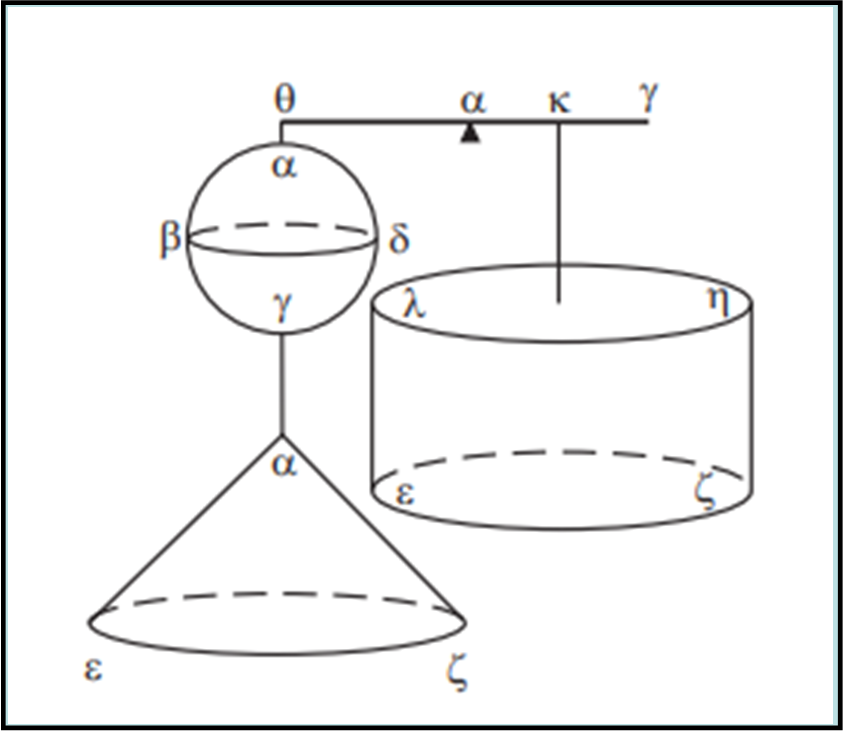
Per capire meglio quanto questi calcoli puramente geometrici fossero importanti per Archimede e i suoi tempi, basta utilizzare una bilancia (non quella di Pippo e Pappo!) e pensare che sfera, cerchi e cilindro siano fatti dello stesso materiale (Fig. 9).

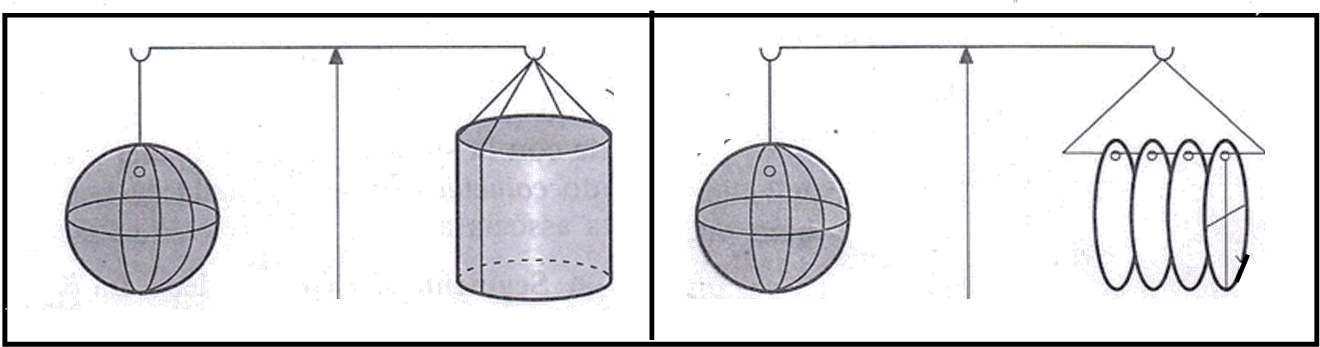
Il volume di una sfera

Sarebbe quasi impossibile seguire tutti i passaggi basati su pesate e  baricentri vari per arrivare al volume della sfera nello stesso modo di Archimede. Ci vorrebbe quasi un libro... Tuttavia, la cosa veramente importante per lui (e per la Scienza successiva) rimane il fatto che lui sia riuscito a calcolarlo attraverso equivalenze a dir poco geniali. Molti "colleghi" provarono in seguito ad arrivare al suo risultato utilizzando da prima l'algebra e poi, in seguito, gli integrali.

Noi abbiamo scelto il metodo di Luca Valerio, matematico dell'inizio del '600, che si dice sia stato usato anche da Galileo Galilei. Notiamo che la determinazione segue passo passo la determinazione "empirica" di Archimede e il suo "metodo" meccanico legato all'equivalenza di solidi.

Anche questo procedimento è di grande eleganza e semplicità. Al punto da sembrare quasi un'ovvietà... Consideriamo la Fig. 10 e occupiamoci della parte sinistra.

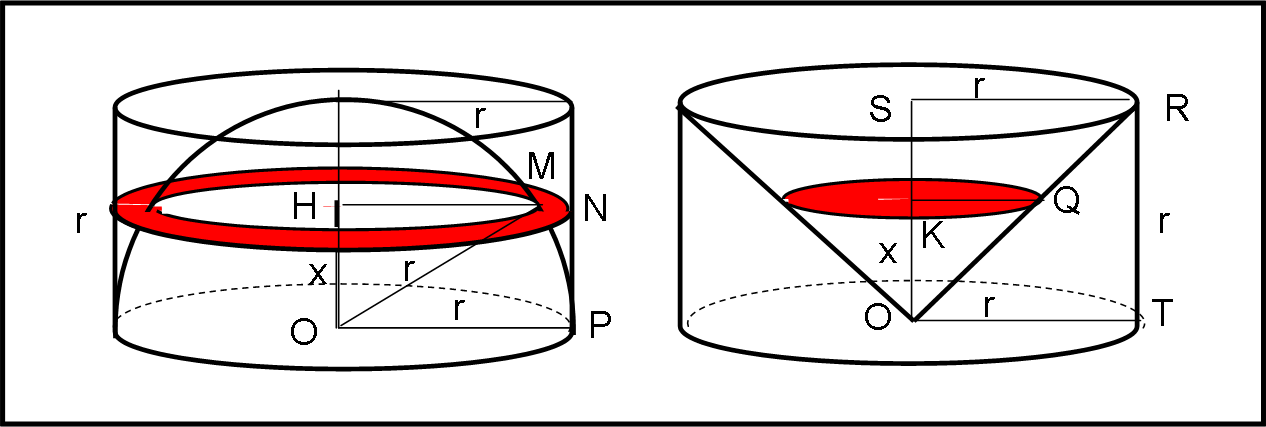
Abbiamo inserito metà sfera all'interno di un cilindro che ha per base il cerchio massimo della sfera e per altezza il suo raggio r. Quello che si vuole fare è calcolare il volume della differenza tra cilindro e sfera. Tracciamo un piano perpendicolare all'altezza del cilindro a un'altezza qualsiasi x (che non sia proprio zero o r). Tra cilindro e sfera si evidenzia molto bene l'anello che abbiamo colorato in rosso. Determiniamone l'area che altri non è  che l'area della sezione del cilindro meno l'area della sezione della sfera. E' facile scrivere:

A_anello = πr² - π HM² = πr² - πr² + πx² 

avendo applicato il teorema di Pitagora al triangolo rettangolo OHM.

Ne segue:

A_{anello = πx²}   

Passiamo, adesso, alla parte destra della figura. Abbiamo sempre lo stesso cilindro di sinistra, ma, questa volta, consideriamo il cono "rovesciato" che ha per base il cerchio superiore del cilindro e come vertice  il centro del cerchio di base. Tagliamo anche questo solido con un piano perpendicolare all'asse del cono e limitiamoci soltanto alla sezione conica che dista nuovamente x dalla base.

Consideriamo i due triangoli  OSR e OKQ. Essi sono simili per costruzione e, di conseguenza, possiamo scrivere:

SR/KQ = SO/OK

Inoltre, i triangoli sono anche isosceli, per cui:

x = KQ = OK

Ne segue subito che l'area della sezione del cono vale:

A _s.cono  = πx² 

Concludiamo, quasi con meraviglia, che l'area dell'anello e l'area della sezione di cono sono uguali.

L’uguaglianza vale, ovviamente, per qualsiasi x, per cui il volume del cono è uguale al volume della differenza tra cilindro e mezza sfera. Risultato in pieno accordo con quanto già trovato da Archimede in modo meccanico.

L'uguaglianza si traduce in poche banali formule.

V_cil - 1/2V_sfera = V_cono

V_sfera = 2V_cil - 2V_cono

V_sfera = 2πr³ – 2/3 πr³ = 4/3 πr³

O, se vogliamo imitare ancora di più Archimede, basta considerare il cilindro che contiene l'intera sfera e scrivere:

V_sfera = 2/3 2πr³ = 2/3 V_cil

Il volume di una sfera è uguale a 2/3 del volume di un cilindro che ha come base un cerchio massimo della sfera e per altezza il suo diametro.

Con pochi passaggi si trova subito che: il volume del cono è uguale a 1/3 del volume di un cilindro di pari base e altezza.

Questa ulteriore conferma dei risultati di Archimede, pone i volumi del cono, della sfera e del cilindro in perfetta successione 1, 2 e 3, ossia il volume del cono equivale a 1/3, quello della sfera a 2/3 e quello del cilindro a 3/3 di se stesso.

Certo, amici miei, se non erano geni persone come Archimede... muniti solo di leve, qualche specchio ustore e rudimentali bilance...

 

...per non parlare di Eratostene di Cirene che, con un bastone, un dromedario e un servitore molto affidabile, 2300 anni fa calcolò con buona approssimazione la misura della circonferenza terrestre!

Vi siete mai chiesti cosa avrebbe potuto fare Archimede con una bilancia moderna? Noi lo abbiamo fatto e ci siamo dati questa risposta QUI.