Quiz: Un Topo-Logico.
Ritorna il nostro amico topo, sempre abile a sfuggire alle grinfie del gatto.
Il gatto malefico prende lezioni da Wile Coyote per organizzare una trappola al nostro amico.

Si procura poi del formaggio, e si reca nell'abitazione preferita dal topo, per organizzare una trappola.
In un solaio ricco di cunicoli che partono dai quattro angoli, pratica dei fori in tali cunicoli, facendo un ponte con il formaggio.
La sua idea è che il topo mangerà il formaggio e cadrà di sotto nelle sue braccia, nella stanza sottostante.
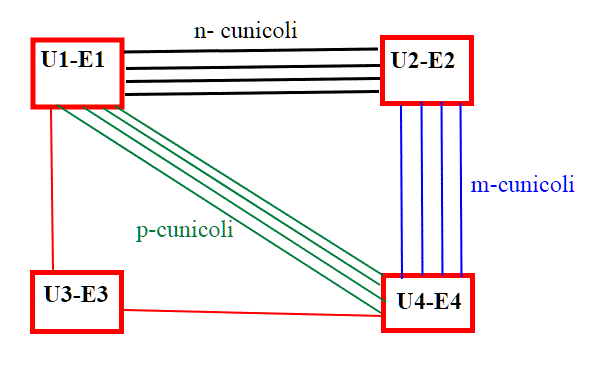
Ma il topo è furbo, riesce ad esempio ad entrare da sinistra, passare sopra e mangiare quasi tutto il formaggio, e uscire da destra(non può più tornare indietro). Oppure potrebbe entrare da destra, mangiare e uscire da sinistra. Fatto sta che essendosi creato un buco, tale cunicolo non sarà più percorribile. Ma vediamo lo schema dei cunicoli, che in linguaggio matematico numeriamo con Ui-Ei (che significa entrata-uscita):
Per essere completamente sicuro, il gatto però, sempre sotto i consigli di Wile Coyote, assolda due aiutanti (di più non può, perchè deve spartire una preda già troppo piccola) e, una volta che il topo è entrato, li mette di guardia su due delle quattro entrate-uscite.( I gatti naturalmente sono troppo grandi per entrare nei cunicoli).
I due gatti guardiani, Mau1 e Mau2:


Abbiamo quattro entrate-uscite , due di esse però presidiate , i numeri n,p,m sono numeri qualsiasi, che non conosciamo. Il topo ha capito che quello stupido gatto ha messo del formaggio in ogni cunicolo. Potrebbe accontentarsi ed uscire dalla via più comoda dopo averne mangiato un po', ma essendo ingordo vuole mangiarlo tutto. Sa che dopo aver tolto un pezzo di formaggio da un cunicolo, non potrà percorrere lo stesso cunicolo . Il suo obbiettivo è quindi di percorrerli tutti una sola volta. Le domande del quiz sono due:
- E'possibile che il topo riesca a mangiucchiare tutti i pezzi di formaggio, ovvero a percorrere tutti i cunicoli?
- Nel caso il gatto riesca nell'intento di percorrere tutti i cunicoli,è possibile posizionare i due gatti-guardiani in modo che il topo sia catturato, oppure non riesca più ad uscire?(i gatti vedono da dove entra il gatto all'inizio).
PS. In un recente articolo del blog potete trovare le indicazioni per risolvere il problema, che altrimenti risulterebbe molto difficile.
Se qualcuno lo risolvesse in autonomia completa potrebbe infatti pubblicarlo direttamente su https://arxiv.org/ !
In Aggiunta al testo; particolare dei cunicoli:
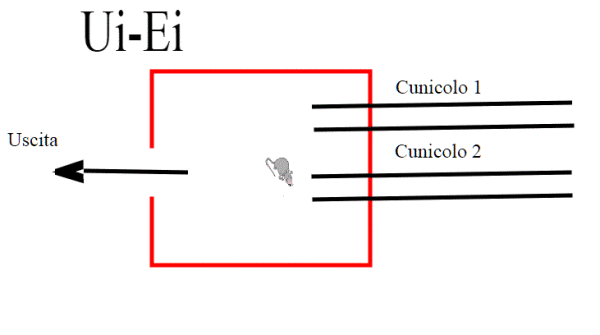
se non fosse chiaro, il topo può uscire dal cunicolo1 ed entrare nel cunicolo2 senza uscire dal solaio.






38 commenti
Non sono sicuro di avere ben compreso. La posizione del topo e dei due gatti di guardia , all'inizio del gioco, è a piacere ? In ogni caso, provando a mettere i gatti secondo le varie possibilità (2 gatti in 4 entrate-uscite), mi sembrerebbe che non sia possibile al topo percorrere tutti i cunicoli una sola volta. Per esempio, se i gatti sono in U2-E2 e U3-E3 e il topolino inizialmente è, per esempio, in uno degli n cunicoli tra U1-E1 e U2-E2 ed è entrato da U2-U2, allora il topo potrà percorrere tale cunicolo arrivando in U1-E1, poi da qui andrà verso U4-E4 su e giù verso U1-E2 fino a percorrere una sola volta tutti i p cunicoli. A questo punto, tornato necessariamente in U1-E1, avrebbe due possibilità: prendere un cunicolo non ancora percorso verso U2-E2, oppure prendere un cunicolo verso U3-E3. Ma in entrambi i casi finirebbe mangiato da uno dei gati, posizionati appunto uno in U2-E2 e uno in U3-E3.
Il quiz chiede per caso se esiste una configurazione iniziale topo/gatti tale che alla fine il topo riesce nel suo intento ?
So che possono esserci delle incomprensioni. I gatti si trovano fuori dall'entrata-uscita dei cunicoli; il topo può raggiungere tranquillamente qualsiasi EI-Ui; se un gatto è davanti il topo torna indietro(se può farlo) .
La domanda principale del quiz è però: il gatto riesce a mangiare tutti i pezzi di formaggio? Questo può farlo restando riparato nei cunicoli. Dopodichè, quando raggiunge la posizione finale, si pone il problema se può uscire o restare intrappolato. Ma se anche i gatti sono topologici, a seconda da dove è entrato il topo potranno capire da dove esce.
le due domande :
sono sequenziali. Nella seconda domanda è sottointeso che si sia verificata la prima condizione.
L'ho specificato meglio anche nel testo originale
Se il topo si accontenta, anche sapendo da dove entra non è possibile sapere da dove uscirà. Ma se il topo mangia tutti i pezzi allora si. In tal caso sarebbe vittima della sua ingordigia. Altra cosa che potrebbe creare confusione: Se arriva in un punto d'uscita che ha più cunicoli collegati, il topo non deve uscire e rientrare; i cunicoli sono collegati internamente agli estremi.
Alla fine della soluzione del quiz Nove ponti a Venezia vengono citate le parole del Grande Eulero ...
"Un qualsiasi grafo è percorribile se e solo se ha tutti i nodi di grado pari, o due di essi sono di grado dispari; per percorrere un grafo "possibile" con due nodi di grado dispari, è necessario partire da uno di essi, e si terminerà sull'altro nodo dispari."
Iniziamo a ragionare come se non ci fossero i gatti guardiani Mau1 e Mau2
Nel grafo dei cunicoli in solaio, i numeri m,n,p non sono definiti, possono essere pari o dispari.
Se assumiamo che m,n,p siano tutti pari, ci troviamo nella classica situazione in cui il grafo è interamente percorribile. Anche se due dei tre numeri m,n,p sono dispari , il grafo sarà interamente percorribile a patto di iniziare da un nodo dispari e terminare il percorso sull'altro nodo dispari.
Senza i guardiani, nelle ipotesi dette, il topo riuscirebbe nell'intento di percorrere tutti i cunicoli una sola volta e mangiare tutti i pezzi di formaggio.
Conseguenze della interferenza dei gatti guardiani
le due domande erano queste
Se ci sono due nodi dispari e i due guardiani li presidiano il topo non potrà più uscire.
Se i nodi sono tutti pari il topo ha delle vie di uscita non presidiate.
Temo di non essere ancora sicuro della correttezza della mia interpretazione
Adesso, avendo letto le aggiunte, mi sembra troppo facile, sempre se ho capito bene, appunto. Questa che segue, infatti, mi pare una soluzione , cioè il tipo riesce a mangiarsi tutti i bocconcini di formaggio, percorrendo una sola volta ciascuno degli m+n+p+2 cunicoli (restando però all'ipotesi della figura, cioè m=n=p=4, o comunque pari):
Mi dispiace Arturo , ma non potevo fare un disegno in altro modo:
"Abbiamo quattro entrate-uscite , due di esse però presidiate , i numeri n,p,m sono numeri qualsiasi, che non conosciamo."
Il topo se ha davanti alle uscite un gatto è destinato o al suicidio, o a restare dentro il solaio. Importante è il fatto che la seconda domanda è condizionata dal fatto che il topo abbia percorso tutti i cunicoli una sola volta.
Maurizio, sei sulla buona strada, ma ricordati che m,n,p possono assumere qualsiasi valore
Direi che resta da vedere il caso in cui dei tre numeri m n p ce ne siano 2 pari.
Avendo un solo nodo dispari , la risposta alla prima domanda sarà: il topo non riuscirà a percorrere interamente il grafo, quindi non riuscirà a mangiarsi tutti i pezzi di formaggio.
Non essendo verificata la prima condizione non si pone la seconda domanda.
Ma i gatti non avrebbero fatto meglio a mangiarsi direttamente il formaggio?
mi rendo conto di essere stato un po' troppo ermetico, e mi dispiace. La domanda principale del quiz resta la prima: É possibile che il topo riesca a percorrere tutti i cunicoli una volta solo?
la seconda parte del quiz va interpretata così: I gatti guardiani all inizio non sono davanti a nessun entrata, altrimenti il topo mangerebbe la foglia e scapperebbe subito. Quando il topo entra e vedono da dove, allora decidono dove mettersi.
Maurizio, le combinazioni di una proprietà che può assumere due valori applicate a tre numeri sono ben di più. Comunque bisogna ragionare sui nodi
Perché il topo possa percorrere tutti i cunicoli una sola volta, ossia perché il percorso del topo sia un sentiero Euleriano, il numero di cunicoli m, m e p deve essere tale che alla fine, nel grafo, il numero dei nodi dispari (qui rappresentati dalle entrate-uscite) sia al massimo 2. Uno dei 4 nodi (l'entrata-uscita U3-E3) è sicuramente di grado pari. Restano gli altri 3 nodi. Di questi , al massimo 2 possono essere dispari. La figura riportata nel quiz indica che i cunicoli m sono 4 e così anche per i cunicoli n e p. Sicuramente è un caso particolare, poiché nel quiz si dice che m, n e p non sono noti ma possono assumere valori qualsiasi. Proprio per questo, se guarda caso m=4, n=4 e p=4, ricadiamo nel caso in cui il grafo ha due nodi di grado dispari (le entrate-uscite U1-E2 ed U4-E4). Quindi, nel caso particolare rappresentato dalla figura, il topo riesce a mangiarsi tutto il formaggio. Alla fine del suo percorso, se parte da U4-E4, si troverà in U1-E1. A quel punto, se anche i gatti saranno stati topologici e uno dei due si sarà posizionato su U1-E1, il gatto resterà intrappolato, non potendo né uscire dal solaio né tornare indietro.
Si tratterebbe a questo punto di generalizzare il discorso, andando a mettere delle condizioni su m, n e p in modo tale che alla fine il numero dei nodi dispari sia al massimo 2.
m può essere pari o dispari. Idem per n e per p. Analizzo le possibili combinazioni.
Caso m pari, n pari, p pari ---> ricadiamo nel caso in figura --> il topo si mangia tutto il formaggio
Caso m pari, n pari, p dispari ---> U2-E2 di grado pari (m+n) ; U4-E4 di grado pari (m+p+1); U1-E1 di grado pari (n+p+1); U3-E3 di grado pari (1+1) ---> tutti i nodi del grado sono di grado pari, quindi il topo riesce a mangiarsi tutto il formaggio
Caso m pari, n dispari, p dispari ---> U2-E2 di grado dispari (m+n) ; U4-E4 di grado pari (m+p+1); U1-E1 di grado dispari (n+p+1); U3-E3 di grado pari (1+1) ---> il grafo ha due nodi di grado dispari, quindi il topo riesce a mangiarsi tutto il formaggio
Caso m dispari, n dispari, p dispari ---> U2-E2 di grado pari (m+n) ; U4-E4 di grado dispari (m+p+1); U1-E1 di grado dispari (n+p+1); U3-E3 di grado pari (1+1) ---> il grafo ha due nodi di grado dispari, quindi il topo riesce a mangiarsi tutto il formaggio
Caso m dispari, n pari, p dispari ---> U2-E2 di grado dispari (m+n) ; U4-E4 di grado pari (m+p+1); U1-E1 di grado pari (n+p+1); U3-E3 di grado pari (1+1) ---> il grafo ha un solo nodo di grado dispari, quindi il topo riesce a mangiarsi tutto il formaggio
Caso m dispari, n dispari, p pari ---> U2-E2 di grado pari (m+n) ; U4-E4 di grado pari (m+p+1); U1-E1 di grado pari (n+p+1); U3-E3 di grado pari (1+1) ---> il grafo ha tutti i nodi di grado pari, quindi il topo riesce a mangiarsi tutto il formaggio
Caso m pari, n dispari, p pari ---> U2-E2 di grado dispari (m+n) ; U4-E4 di grado dispari (m+p+1); U1-E1 di grado pari (n+p+1); U3-E3 di grado pari (1+1) ---> il grafo ha due nodi di grado dispari, quindi il topo riesce a mangiarsi tutto il formaggio
Caso m dispari, n pari, p pari ---> U2-E2 di grado dispari (m+n) ; U4-E4 di grado pari (m+p+1); U1-E1 di grado dispari (n+p+1); U3-E3 di grado pari (1+1) ---> il grafo ha due nodi di grado dispari, quindi il topo riesce a mangiarsi tutto il formaggio
Se non mi stanno sfuggendo altre possibili combinazioni, mi pare che in ogni caso la risposta alla prima domanda è si.
si Arturo, il tuo é un sistema valido, che però può essere" condensato". Resta aperta la seconda domanda.. Se i gatti vedono da dove entra il gatto possono determinare da dove uscirà? E bloccarne l uscita?
sempre nel caso che il gatto abbia percorso tutti i cunicoli.Continuo a dimenticarmi di dirlo.
Mi sembra che il numero di combinazioni "distinte" per i nodi siano solo 4.
Mnp. 3 pari
Nodi 2p e 2d
Mnp. 2 pari un dispari
Nodi 2p e 2d
Mnp 2 dispari un pari
Nodi 2d e 2p
Mnp 3 dispari
Nodi 2p e 2d
Sembra che sia sempre possibile il percorso completo.
E smettila di scrivere "gatto" per dire "topo"...
hai ragione; topo!
Dato che ci sono sempre due nodi di grado dispari il topo deve iniziare e terminare con essi. In tal modo mangerá tutto.
Però se i gatti si piazzano inquei nodi non potrá più uscire.
Aspettiamo domani Maurizio; siamo già avanti, non mangianomoci subito tutto il quiz. In fin dei conti è passato solo un giorno.. É questione di audience ..ricordati comunque il discorso di Arturo.. Le variabili libere dono n, m, p. Dobbiamo dimostrare che comunque varino otteniamo al massimo due nodi dispari
Ok Umberto, lasciamo tranquillo il topo, vuol dir che per stasera mangerò il formaggio...
Mau
e grazie mille a tutti delle idee..chissà che non arrivi qualcun altro.
Nel mio precedente commento c'e' un errore nel caso m dispari-n pari-p dispari. Infatti anche in questo caso ho due nodi di grado dispari , e non solo 1.
Per la "condensazione", prendendo il nodo U1-E1 è chiaro che ai fini del suo grado è indifferente scegliere tra il caso n pari-p dispari e il caso n dispari-p pari. Infatti la somma dei cunicoli confluenti in tale nodo sarà sempre n+p+1. Analogamente, per il nodo U2-E2 è indifferente scegliere tra il caso m pari-n dispari e il caso m dispari-n pari. La somma dei cunicoli confluenti in tale nodo sarà sempre m+n. Stesso ragionamento per il nodo U4-E4, per esso è indifferente scegliere tra il caso m pari-p dispari e il caso m dispari-p pari. La somma dei cunicoli confluenti in tale nodo sarà sempre m+p+1.
Quindi, nel complesso, i casi possibili si riducono di numero.
Per la seconda domanda, se m, n e p sono tali che il numero dei nodi di grado dispari è due, allora, per le proprietà del sentiero euleriano, che parte da uno dei nodi dispari e finisce nell'altro, sapendo da quale nodo parte il topo i gatti avranno la possibilità di determinare da quale nodo verrà fuori. Se, invece, m, n e p sono tali che tutti i nodi del grafo sono di grado pari, allora , poiché in questo caso i percorsi dovrebbero iniziare e finire nello stesso nodo, i gatti , vedendo da quale nodo parte il topo, sapranno anche in questo caso dove piazzarsi per bloccarlo all'uscita.
ok Arturo, aspettiamo anche gli altri.
Ricordo che il quiz è aperto a Tutti. Da quando Maurizio a Introdotto il teorema di Eulero e Arturo scritto l'ultimo commento siamo in grado di risolvere matematicamente e senza ombra di dubbio la prima parte del quiz. Sostanzialmente Arturo ha già risolto la prima parte ma possiamo fare anche in altri modi.Basta un po' di aritmetica, un po' di logica , e saper esprimere un numero pari e un numero dispari in forma generica. Il quiz è ancora aperto! Poi aspetto anche la seconda parte, ma per adesso risolviamo bene questa.
cari Tutti,
avrei voluto partecipare... ma ho per amico molto stretto un "bombo", quelle grosse api che saettano da un fiore all'altro, e lui questi problemini li risolve come fare uno più uno... Non per niente è capace di risolvere continuamente il problema del commesso viaggiatore... e dico poco http://www.infinitoteatrodelcosmo.it/2016/03/30/ma-cose-lintelligenza/
C'è chi può contare su Pautasso e chi su un bombo ... così è la vita

Questo schema mostra le 8 configurazioni possibili per i tre canali m n p (pari o dispari ) .
Il numero di canali dei tre lati superiori m n p è segnato con un tratto (dispari) o 2 tratti (pari).
I 2 lati inferiori sono comunque costituiti da un solo canale
I gatti sono indicati dalle lettere M.
Nei 2 casi in cui tutti i nodi sono pari, i gatti potrebbero scegliere di presidiare i nodi con maggior numero di collegamenti. Li ho segnati con un punto di domanda.
d accordo Vincenzo, ma il quiz ed Eulero stesso chiede solo se il.problema è possibile. Di certo non chiede di trovare il percorso euleriano.
ma io stavo scherzando, ovviamente... (parlo piano perché se mi sente il bombo mi prede in giro... )
)
"Vadi" per il bombo...ma torniamo a bomba!
Un piccolo suggerimento: G1,G2,G3,G4 rappresentano i gradi dei quattro nodi; come detto già da Arturo, possiamo esprimere tali gradi in funzione di n,m,p che ricordiamocelo, sono numeri interi positivi qualsiasi.
Ora, come dicono Maurizio e Eulero affinchè tutti i cunicoli siano percorribili tutti solo una volta, dobbiamo avere al massimo due nodi di grado dispari. C'è un modo per dimostrarlo in modo semplice, senza analizzare tutti i casi di parità-disparità per m,n,p?
Facendo riferimento alla figura del commento precedente, il grado di ciascun nodo risulta dalla somma del numero di canali in ciascun lato che lo collega.
G1= 1+p+n
G2= n+m
G3= 2
G4= 1+p+m
I numeri pari li esprimo con 2I (I numero intero >0)
I numeri dispari li esprimo con 2I+1
Dato che G3 è sempre pari, resta da stabilire come variano G1, G2, G4 al variare di m,n,p.
se p è pari vale 2I, se è dispari vale 2I+1
se P è pari (=2I)
G1= 2I+1 + n dispari se n pari
G2= n+m dispari se n e m non sono ambedue pari o ambedue dispari
G3= 2
G4= 2I+1 + m dispari se m pari
In ogni caso i nodi di grado dispari sono zero, oppure due perché:
se G1 e G4 sono dispari, allora G2 è pari, mentre, se uno è pari e l'altro e dispari, allora G2 è dispari.
se P è dispari (=2I+1)
G1= 2I+2 + n dispari se n dispari
G2= n+m dispari se n e m non sono ambedue pari o ambedue dispari
G3= 2
G4= 2I+2 + m dispari se m dispari
In ogni caso i nodi di grado dispari sono zero, oppure due perché:
se G1 e G4 sono dispari, allora G2 è pari, mentre, se uno è pari e l'altro e dispari, allora G2 è dispari.
Però anche con questo ragionamento vengono analizzati i vari casi...
Premesso che G3 è sempre pari, analizziamo la somma G1+G2+G4
G1+G2+G4 = (p+n +1) +(n+m) + (p+m +1) = 2p + 2n +2m + 2 è sempre un numero pari.
Significa che i nodi G1 G2 G4 hanno tutti grado pari oppure due di essi hanno grado dispari
mi piace di più la seconda opzione, quella di Mau. Se é valida e anche più immediata della mia soluzione . Non sono sicuro se tu abbia fatto confusione con le lettere
Sì, avevo messo un G3 invece che un G4... ora ho corretto il commento, comunque lo riscrivo qui sotto:
Premesso che G3 è sempre pari, analizziamo la somma G1+G2+G4
G1+G2+G4 = (p+n +1) +(n+m) + (p+m +1) = 2p + 2n +2m + 2 è sempre un numero pari.
Significa che i nodi G1 G2 G4 hanno tutti grado pari oppure due di essi hanno grado dispari
Grazie Mau.rendiamoci conto della semplicità della soluzione; se non ci fosse stato Eulero.. Ma adesso pensiamo alla seconda domanda, anche se è. Un po' ambigua.
Ipotesi : il topo decide di fare il percorso completo per mangiare tutto.
Se tutti i nodi hanno grado pari deve uscire da dove è entrato e i gatti lo aspettano li
Se ci sono 2 nodi dispari entra da uno e esce dall'altro. I gatti si piazzano sul nodo dispari da cui non è entrato.
Quello che dici è vero Maurizio; però adesso sì avere nodi tutti pari o due dispari dipende dai valori di m,n,p ovvero dal fatto se sono pari o dispari m,n,p, ma m,n,p non li conosce nessuno, nè il topo, nè i gatti , nè noi. Sono arbitrari. Quindi..
Però quando il gatto-capo ha messo il formaggio ha visto quanti pezzi ha usato per ciascun collegamento. Lui conosce i valori di m n p. Immagino che ne abbia informato i soci.
Invece il topo potrebbe conoscere quei valori da prima che il gatto ci mettesse le trappole mangerecce.
Altrimenti, se nessuno sa nulla il risultato è casuale. Il topo entra senza sapere se riuscirà a fare il giro completo e i gatti non hanno indizi su dove mettersi in agguato.
O forse non ho ben chiaro il quesito...
No, ti ho detto che è ambiguo. Il gatto capo potrebbe anche saperlo, ma magari non riesce a tradurre in numeri i mao-mau. L'importante è che sia emerso che mentre la fattibilità sia sempre possibile, la partenza -arrivo dipenda da come sono fatti n,m,p. era questo che volevo mettere in luce
Ok ora mi è chiaro