QUI il testo del quiz

Una pizza dai tagli flessuosi e curvilinei che Maurizio ha gustato fino in fondo. Noi cerchiamo di darle anche un risvolto astronomico e non solo g-astronomico, richiamando addirittura Apollonio di Perga e i sui epicicli.

La nostra pizza richiama uno dei grandi astronomi greci: Apollonio di Perga. Sicuramente un genio, ma anche una specie di “assassino” della dinamica planetaria. E’ stato lui a introdurre il deferente (orbita circolare) descritto dal centro di un’altra orbita più piccola, sempre circolare (epiciclo), che viene descritta da un pianeta (Fig. 1).

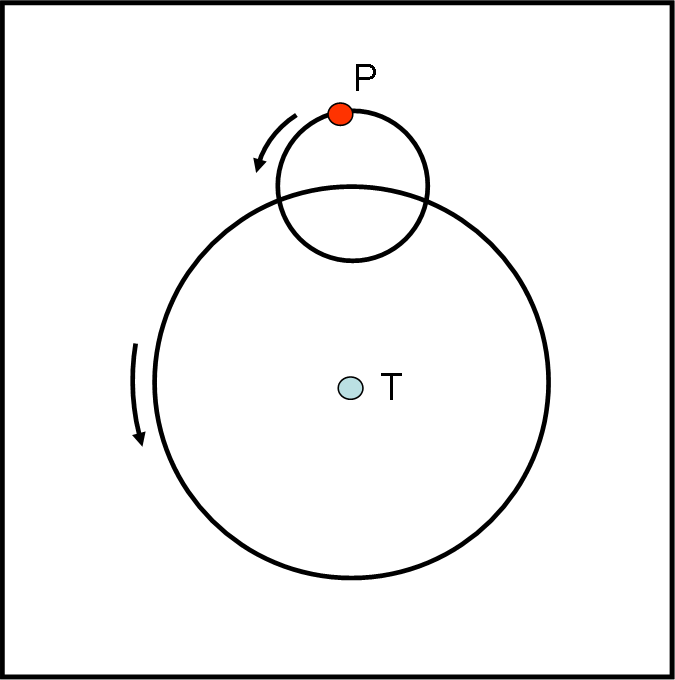
Idea meravigliosa che riesce a spiegare piuttosto bene gli stani movimenti dei pianeti visti dalla Terra (supposta fissa) e la loro luminosità variabile: un moto "quasi" ellittico ottenuto attraverso la combinazione di moti circolari. Sappiamo quanti secoli ci siano voluti per distruggere questa splendida approssimazione (ne abbiamo parlato QUI e QUI), fatta sua e migliorata da Tolomeo e –purtroppo- presa come un dogma dalla chiesa, e quanto terrore abbia creato il cercare di smontarla. I nostri Pippo e Pappo la usano solo per tagliare una pizza… glielo possiamo concedere!

Bene… consideriamo la Fig. 2.

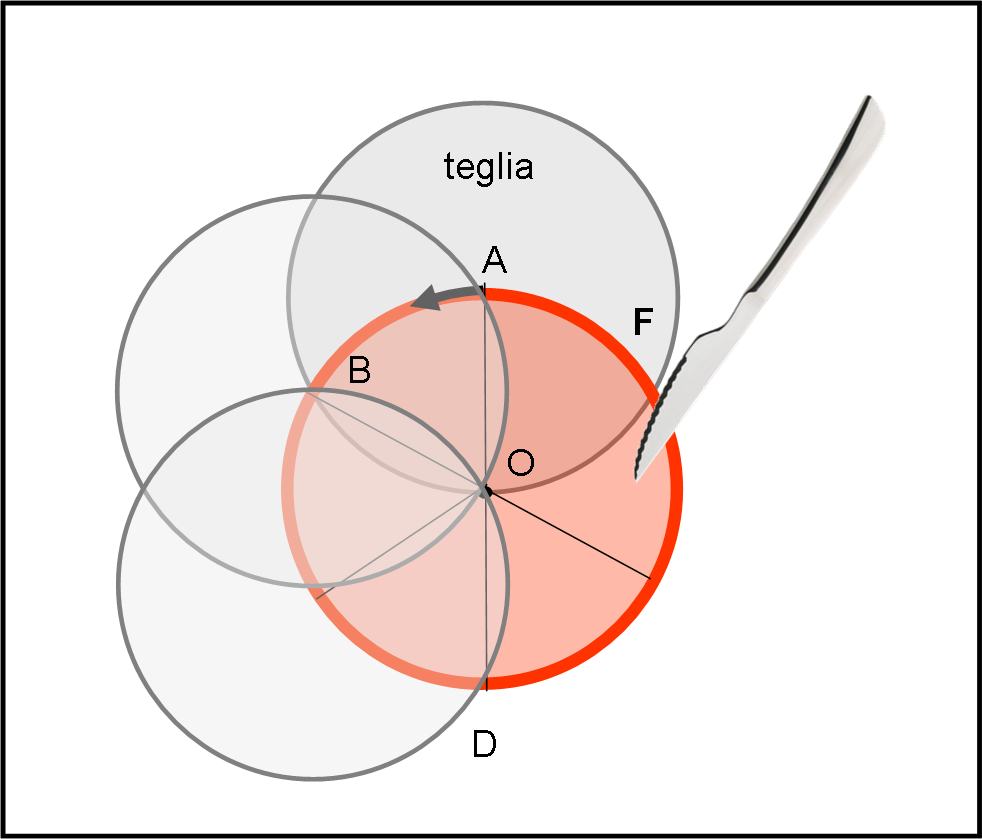
Il deferente è la pizza e la teglia è l’epiciclo. Una configurazione un po’ particolare, dato che l’epiciclo ha lo stesso raggio del deferente e non vi è niente che si muove su di lui. O, meglio,si muove -saltuariamente e per brevi tratti, un pianeta-coltello.

Poco importa, dato che noi vogliamo che la teglia acquisti posizioni particolari rispetto alla pizza… ops... deferente. Sia O il centro della pizza (magari basta un bel cappero per segnalarlo). Facciamo coincidere il centro della teglia (forato) con A, sul bordo della pizza.  Pippo tiene ferma la teglia e Pappo usa il coltello speciale per segnare la pizza lungo il tratto OF. Si sposta la teglia lungo il suo deferente-pizza fino a che il suo centro cada in B. Posizione facile da ottenere dato che in quella posizione la teglia deve passare da A e O. Altro segno ben marcato da O ad A e il primo “sesto” di pizza è stato segnato (AOF). Con grande abilità e sicurezza l’epiciclo viene portato in basso in modo da passare per O e D e si segna il tratto OB. E via dicendo come mostrato in Fig. 3.

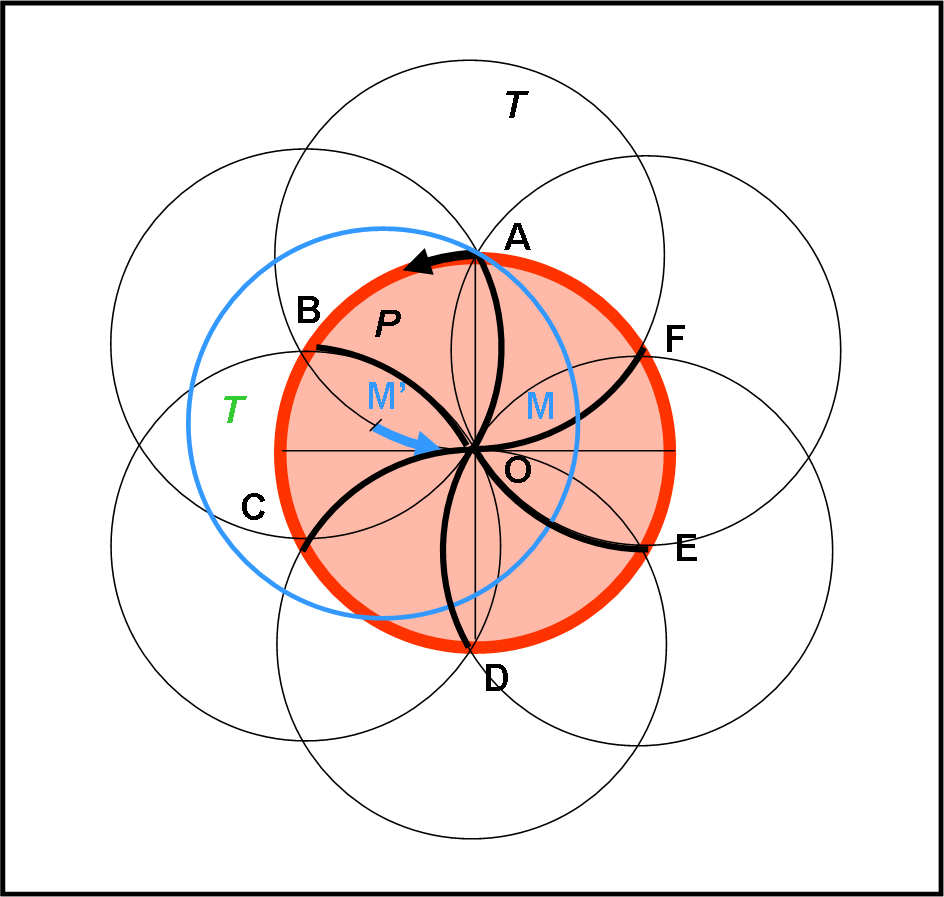
Per proseguire con i tagli, basta ora considerare come deferente la teglia nella posizione in cui il suo centro è A (basta tracciarlo con la matita) e come epiciclo la teglia vera e propria (segnata in azzurro), il cui centro si sposta da M' verso M, percorrendo il deferente di centro A. Con il metro da sarta piegabile è facile determinare il punto di mezzo M del primo “sesto” di pizza e tracciare con il coltello il segno AM azzurro. Il sesto si è trasformato in due dodicesimi.

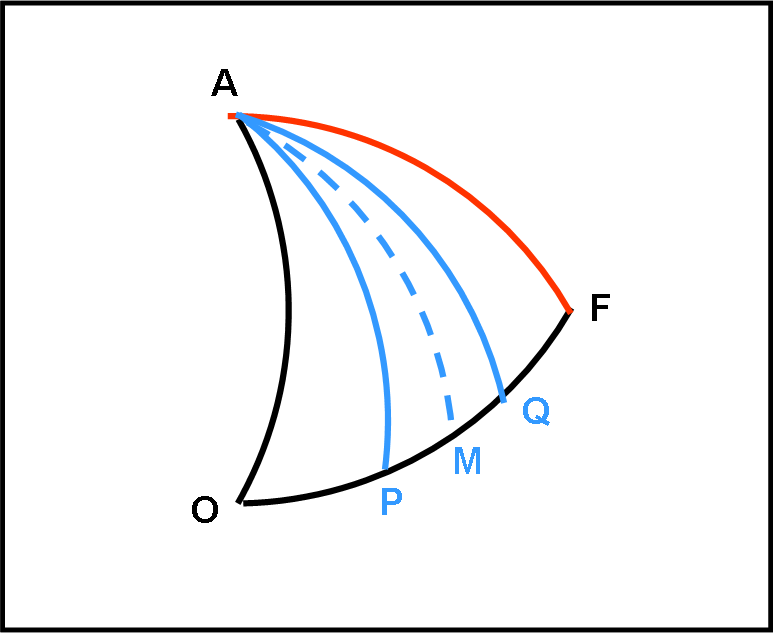
L’operazione non viene, però, conclusa, dato che giungono i sei inaspettati amici. Poco male! Basta dividere in tre parti uguali l’arco OF (OP, PQ e QF) e il sesto di pizza AOF si divide in tre diciottesimi, lasciando sempre solo un pezzo con il bordo, come mostrato in Fig. 4.

Per vedere il risultato finale, preferisco utilizzare la più rozza, ma appetitosa immagine mostrata da Maurizio nei commenti (Fig. 5)

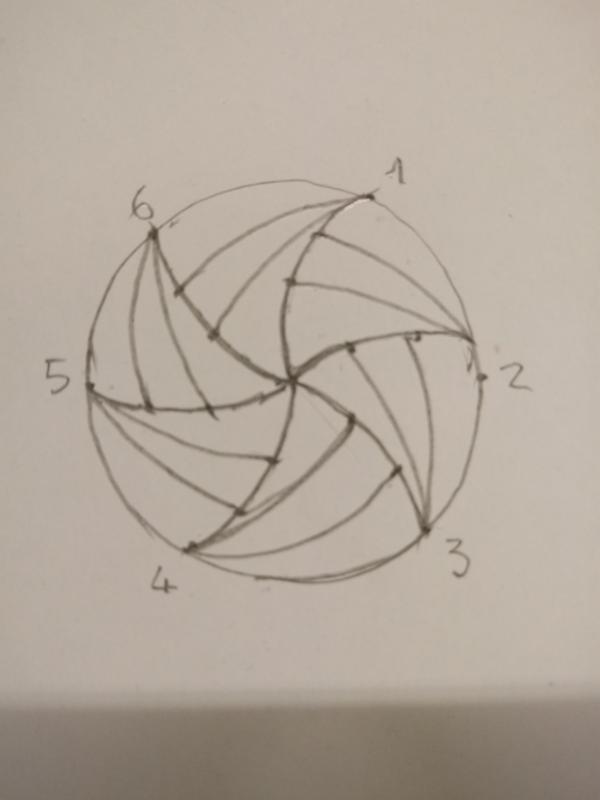
Notiamo che potevamo ottenere anche 24 o 30 pezzi di pizza, tutti perfettamente uguali, anche se sarebbero diventati sottilissimi…