Categorie: Matematica
Tags: aree geometria piana parallelogramma
Scritto da: Vincenzo Zappalà
Commenti:10
QUIZ geometrico: un parallelogramma tagliuzzato **
In attesa che Peppa faccia la sua tanto attesa ricomparsa (si sta facendo bella...), beccatevi questo quiz geometrico. Qualsiasi strategia è accettata, ma l'eleganza è sempre premiata...
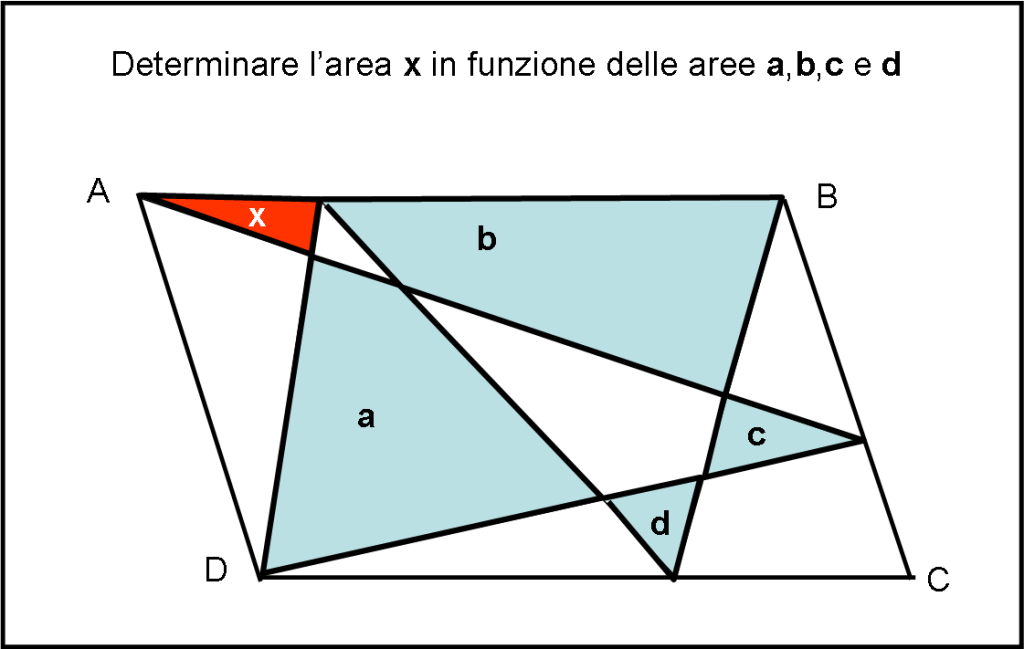
Il quiz è molto semplice e viene espresso chiaramente dalla figura che segue, dove abbiamo un parallelogramma qualsiasi che è stato tagliuzzato da molte linee. Esse individuano alcune parti colorate in azzurro le cui aree sono state chiamate a, b, c, d e sono considerate note. Si chiede semplicemente di esprimere l'area incognita x (del triangolo colorato in rosso) in funzione delle quattro aree note (a,b,c,d).
Qualsiasi tipo di approccio (algebrico, trigonometrico o puramente geometrico è ammesso).
Eleganza, però, eleganza....
QUI la soluzione






10 commenti
Suppongo che la posizione dei vertici dei triangoli c e d sui lati DC e BC sia casuale, come pure il vertice del triangolo rosso sul lato AB. Giusto ?
giusto!
Indico con:
B' il punto tra A e B
C' quello tra B e C
D' quello tra C e D
Posiziono ad hoc uno di questi punti in modo da azzerare alcune aree e valuto ogni volta l'area incognita che chiamo x.
1 . solo B' va in B : azzero le aree b,d
X=a+c Due triangoli opposti ad un vertice, di uguale area
2 . solo C' va in B: azzero b,c
X=0 = a-d
3. Solo D' va in D: azzero a,d
X+b=c. da cui x=c-b
Conosco ora i segni dei singoli contributi che danno x
X= a-b+c-d
Parto da +a , ruotando in senso orario e alternando i segni + e -
Al momento non posso inserire immagini ma penso si capisca il ragionamento.
Più velocemente, indico con C' il punto tra B e C.
L'area di AC'D è pari all'area esterna ad AC'D
La somma delle aree interne equivale alla somma delle aree esterne.
Interne: a,c Esterne: x,b,d
Quindi, a+c =x+b+d da cui ho x
X= a+c-b-d
Aree rosse R . Gialle G . Verdi V . Blu B
R+G = V+B. evidente
R-V=B-G . e inoltre...
R+V=B+G . sommando...
2R=2B. Quindi . R=B . e . G=V
V . vale X+ b +d . G vale .a+c
X+b+d = a+c . X= a+c -b-d
Caro Sig. Mau,
sarebbe così gentile da spiegare perché certe aree sono uguali... cerchi di essere più terra-terra...
E nel caso in cui il parallelogramma fosse un quadrilatero qualsiasi?
e perché no? provaci Leandro...
Aree Rosse R .Verdi V .Gialle G . Blu B
R+G = V+B. Perchè....
AC'D ha area uguale alla somma di BAC'+ C'DC perchè le altezze sono uguali e la base AD =BC'+C'C.
R-V=B-G . semplice algebra...
e inoltre...
R+V=B+G . Perchè....
I due triangoli. Rosso-verdi hanno la stessa altezza dei due triangoli giallo-blu ed inoltre le due coppie hanno come basi due lati orizzontali (identici) del parallelogramma.
sommando... membro a membro
R-V .+R+V .= B-G .+B+G . Ossia...
2R=2B.
Quindi . R=B .
e , dato che .R+G = V+B , risulta. G=V
V. vale X+ b +d . e G vale a+c
Sostituendo questi valori, ottengo:
X+b+d = a+c
Ricavo quindi x in funzione di abcd...
X= a+c -b-d
grazie mio caro... sempre molto gentile...