QUI il testo del quiz

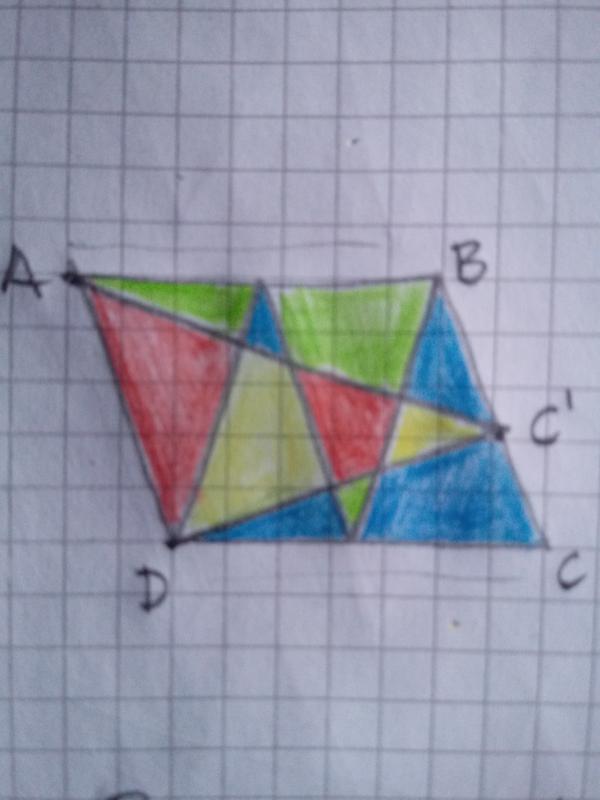
Approfitto della figurina colorata di Maurizio (come sono democratico io…) per aggiungere un paio di concetti che aiutino nel comprendere la soluzione trovata dal nostro “mago”. Tutto il gioco sta nel determinare due insiemi di “pezzi” che siano entrambi uguali alla metà dell’area del parallelogramma. In tal modo possiamo uguagliare i due insiemi e ricavare la parte x, dato che tutto il resto è noto, oppure si semplifica.

L’area di un parallelogramma è uguale a base per altezza. Dobbiamo ricavare qualcosa che sia uguale a base per altezza diviso due.  Riproduciamo la figura mauriziana e guardiamo bene le parti gialle e le parti azzurre, messe assieme…Otteniamo esattamente due triangoli tali che la somma delle loro basi è proprio la base del parallelogramma, mentre l’altezza è la stessa. Nel segue che l’area delle parti gialle e azzurre è proprio la metà dell’area del parallelogramma.

Tuttavia la stessa cosa capita per i due triangoli composti dalle parti verdi e rosse, anche loro sono nelle condizioni dei due precedenti.

Per non farci mancare niente, nel nostro parallelogramma si è abbondato… Vi sono anche altre due parti che sono uguali a metà dell’area del parallelogramma: i due triangoli composti dalle parti verdi e azzurre e il triangolo singolo composto dalle parti gialle e rosse.

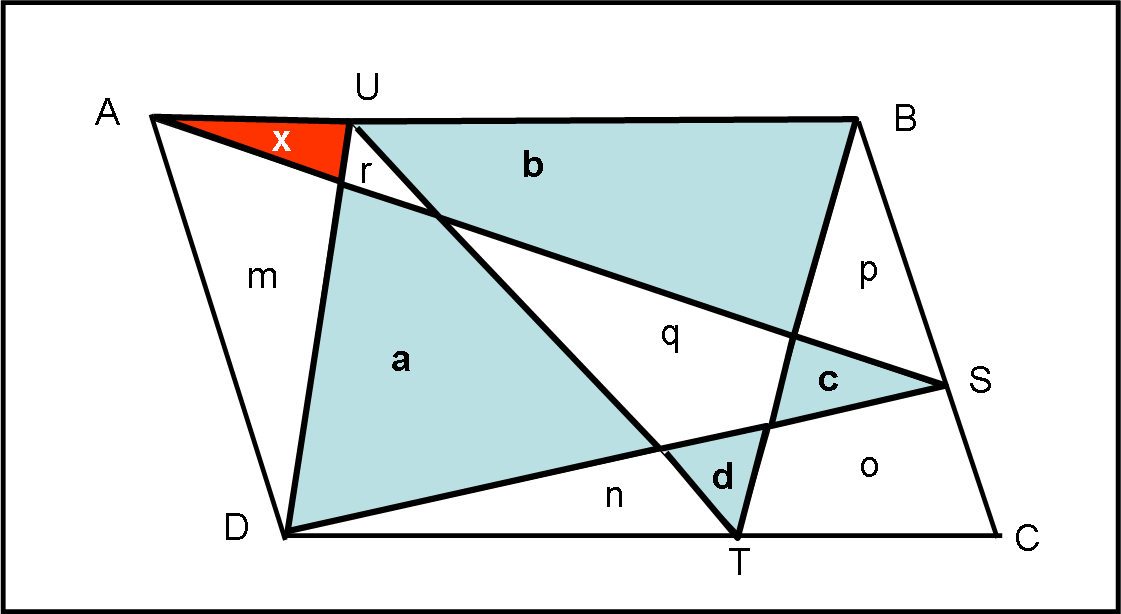
Uguagliando due di queste parti pari a metà parallelogramma (potete scegliere quelle che preferite), dove almeno una contenga la parte incognita x, vedrete (come ha fatto Maurizio QUI) che le parti non note si semplificano tra di loro e alla fine rimane proprio:

x = a + c - b - d

Ad esempio, possiamo considerare l'area dei due triangoli ABS e SCD  e uguagliarla all'area dei triangoli DUT e TBC

p + b +r + x + o + d + n  = a + n + r + o + c + p

x = a + c - b - d

C.V.D.

Ah… questi maghi… ne sanno una più del diavolo!