Sarò sintetico, visto che nei commenti al quiz potete trovare ampie discussioni sul problema. Il quiz lo trovate qui   .

La soluzione si basa interamente sul teorema di Eulero, che trovate in questo articolo , nove ponti a Venezia , ed è stato subito citato da Maurizio:

"Un qualsiasi grafo è percorribile se e solo se ha tutti i nodi di grado pari, o due di essi sono di grado dispari; per percorrere un grafo "possibile" con due nodi di grado dispari, è necessario partire da uno di essi, e si terminerà sull'altro nodo dispari.", mentre Arturo aveva già intuito che il tutto dipendeva dalle combinazioni di m,n,p, che producono nodi pari o dispari. Bisognava però arrivare ad una forma più sintetica, del tutto.

Se ci basiamo sul disegno:

G1,G2,G3,G4 rappresentano i gradi dei quattro nodi; come detto già da Arturo, possiamo esprimere tali gradi in funzione  di n,m,p che ricordiamocelo, sono numeri interi positivi qualsiasi.

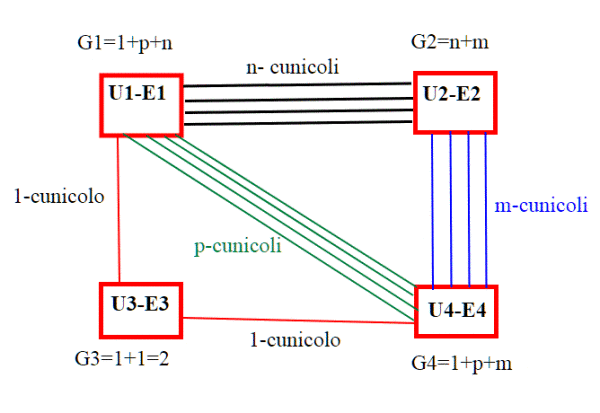
Ora, come dicono Maurizio e Eulero affinchè tutti i cunicoli siano percorribili  tutti solo una volta, dobbiamo avere al massimo due nodi di  grado dispari. C'è un modo per dimostrarlo in modo semplice, senza analizzare tutti i casi di parità-disparità per m,n,p? Si, cito direttamente quello di Maurizio, che è ancora più immediato del mio.

"Premesso che G3 è sempre pari, analizziamo la somma G1+G2+G4

G1+G2+G4 = (p+n +1) +(n+m) + (p+m +1) = 2p + 2n +2m  + 2       è sempre un numero pari.
Significa che i nodi G1 G2 G4 hanno tutti grado pari  oppure due di essi hanno grado  dispari"

Quindi, qualsiasi siano m,n,p il  problema ha sempre soluzione. Ma veniamo alla seconda domanda:

Nell'ipotesi che il topo faccia il percorso completo e i gatti vedano da dove entra, è possibile prevedere da dove uscirà?

Dice Maurizio:

"Se tutti i nodi hanno grado pari deve uscire da dove è entrato e i gatti lo aspettano li.

Se ci sono 2 nodi dispari entra da uno e esce dall'altro. I gatti si piazzano sul nodo dispari da cui non è entrato."

E questo è vero; la domanda però era un po' ambigua; i gatti non conoscono i valori di m,n,p, ma mentre se il percorso fattibile è indipendente da essi, non lo è da dove parte e da dove arriva il topo. Per esempio se p,n.m sono pari,G1 è dispari,G2 è pari, G4 è dispari. G2 sappiamo che è pari, essendo G2=2. Quindi può partire da G1 e arriva in G4. Ma non è più indipendente dai valori di m,n,p. Lascio a voi verificare per quali valori di m,n,p abbiamo quattro nodi pari.