Questo articolo è stato inserito nella pagina d'archivio dedicata all'Astronomia Classica

 

Questo racconto è una incursione nel mondo delle meridiane, che vi darà la risposta alla domanda che mai avete osato fare: cosa è mai quella specie di otto che campeggia sotto lo stilo in corrispondenza della linea del mezzogiorno? Forse la firma del pittore che ha disegnato il quadrante? Oppure una raffigurazione magica il cui significato è andato perduto? Serve forse a qualche scopo pratico? Quali sono i criteri con cui viene tracciato?

Ebbene, se avrete un po' di pazienza e leggerete fino in fondo questo lungo articolo (che raggruppa quelli già pubblicati a suo tempo), nonostante si rida e si scherzi con il nostro semplice e saggio Oreste, alla fine avrete tutte le risposte (serie) a questi interrogativi.

Colgo, in questa occasione, l'opportunità di esprimere un doveroso ringraziamento, a nome mio e dei personaggi di questa storia, a Daniela, per la sua paziente e preziosa revisione e per i consigli con cui ha efficacemente contribuito a rendere più leggibile il testo e più complete le figure.

Grazie a lei, alla fine, sono riuscito anche io a capire cosa avevo scritto.

 

Oreste Pautasso da Cuneo alle prese con l'Analemma

 

Capitolo 1

Anche senza la neve era un Natale fantastico.

Un sole sfolgorante illuminava ogni cosa, infondendo ottimismo e voglia di fare.

Oreste Pautasso uscì di casa per fare due passi nella bellissima piazza Galimberti, il “salotto di Cuneo”.

La Piazza Tancredi Galimberti, già famosa da tempo, è destinata a diventare ancora più famosa perché Wikipedia ci “informa” (potete verificare) che ha una superficie di 24 milioni di metri quadrati.

Pensate che un quadrato di 5 Km di lato ha una superficie di 25 Km quadrati o, se preferite, 25 milioni di metri quadrati, proprio come Piazza Galimberti-Wiki.

Dato che la superficie di tutto il comune di Cuneo è circa 120 Km quadrati, questa piazza, da sola occuperebbe un quinto del territorio comunale!

Meno male che nella stessa pagina di Wikipedia, meno in evidenza, c'è anche il vero valore della superficie della piazza, mille volte più piccola, 24.000 metri quadrati. ( questo evidente errore è stato finalmente corretto ed ora nella pagina di Wikipedia compare solo il valore esatto).

In ogni caso uno spazio enorme, in cui Pautasso avvertiva sempre un senso di assoluta libertà, come quello che ispira il mare aperto.

Il mare... Lo aveva visto solo poche volte. Si era fermato a Venezia la prima volta quando era andato al matrimonio di sua sorella, che aveva sposato uno di Oderzo, un certo Mattia. Il paese era a un'ora di macchina dalla laguna così, ogni volta che andava a trovare i parenti, già che era sulla strada, si fermava qualche ora a guardare il mare.

“Questo cognato Mattia mi sembra un po' fanatico della piazza di Oderzo, l'hanno chiamata piazza Grande” pensava Pautasso. “mi fa proprio ridere, piazza Grande... la mia piazza Galimberti, a Cuneo, è cinque volte più grande.”

E aveva proprio ragione, matematicamente.

“Però nella piazza di mio cognato hanno fatto una bella meridiana che ti avvisa che è mezzogiorno. Si capisce quando è mezzogiorno perché l'ombra della punta della guglia del duomo finisce su un punto particolare. E ogni giorno questo punto cambia! Così, per sapere dove si trova quel giorno lì, hanno fatto un disegno per terra, una specie di grande “otto” sbilenco, che mio cognato (che è astronomo, ma gli voglio bene lo stesso) ha provato a spiegarmi cinque o sei volte, che alla fine gli ho detto che avevo capito, anche se non era vero, giusto per farla finita.”

Il ricordo della meridiana gli fece venire un'idea.

“Oggi, che tanto è Natale e non devo andare al CAC , il Centro Archeofili di Cuneo, dove svolgo la mia missione di lavoratore a pagamento, a fare le fotocopie per gli archeologi, potrei costruire una meridiana come quella della piazza di Oderzo. Prima ne faccio una piccola, poi, se mi viene bene, la faccio vedere al presidente del CAC, Vinicio Barbareschi, che essendo amico del sindaco, magari gliela mostra e gli inculca l'idea di fare una meridiana uguale, ma più grande, in piazza Galimberti, così i turisti impazzano e mio cognato crepa di invidia.”

Detto fatto, tornò a casa e si mise all'opera.

Pautasso non sapeva che il giorno di Natale, oltre ad essere importante per tutti i motivi che ben sappiamo: i doni di Babbo Natale, i canti natalizi, il panettone, il presepe e l'albero, i saldi nei negozi, etc… etc... è un giorno speciale anche per le meridiane.

Suo cognato avrebbe potuto spiegarglielo molto bene, avrebbe potuto dirgli che, proprio quel mezzogiorno, l'ombra del pinnacolo del duomo andava a cadere nel punto estremo della figura a “otto” disegnata sul selciato davanti alla chiesa di Oderzo, ma si erano già scambiati gli auguri per telefono la mattina presto, così non si sentirono.

Per prima cosa Pautasso scelse il posto studiando la mappa di Cuneo. Doveva essere un posto soleggiato per tutta la giornata, in tutte le stagioni. Un posto pianeggiante come la piazza Galimberti, senza case attorno che facessero ombra, né alberi o macchine parcheggiate. Alla fine trovò uno spiazzo adatto allo scopo, proprio dove la circonvallazione scavalca il torrente Gesso e gira attorno al cimitero, mettendosi parallela a “via Madonna della riva”.

Non era molto lontano da casa sua, e poi i dintorni del cimitero erano proprio un luogo tranquillo, senza traffico, che si animava solo in occasione della ricorrenza dei defunti. “Bravo Pautasso” disse tra sé. “questo bel campo che hai trovato in quell'angolino dietro al cimitero, alla curva di Ponte Vecchio, è proprio ad'OK, un vero campo-santo” e si mise a ridere di gusto per la battuta che gli era venuta involontariamente.

Prima che arrivasse mezzogiorno, si portò nella zona con una palina da topografo bianca e rossa, lunga un metro che gli era rimasta in casa da quando avevano misurato i confini del giardino, con l'intento di piantarla ben diritta per terra in mezzo al campo.

“Neh, che non sei mica stupido, Pautasso” si disse mentre procedeva con le operazioni, “A chi sarebbe venuto in mente di portarsi due fili a piombo per essere sicuri che la palina è diritta diritta? Con uno solo non si sa mai... E se smette all'improvviso di funzionare? Invece con due non devi preoccuparti, c'è sempre quello di riserva.”

Con immensa cura piantò lo stilo, lo verificò molte volte per essere sicuro che risultasse proprio perpendicolare al terreno, che aveva reso pianeggiante come un tavolo da biliardo, e attese il mezzogiorno. “Sei proprio una volpe, Pautasso! Questa idea della sveglia, che ti avverte un minuto prima di mezzogiorno, è geniale, così fai in tempo a trovare il punto preciso dove va a cadere l'ombra della punta della palina e puoi trafiggere il terreno per lasciare traccia.” In effetti aveva portato con sé anche dei chiodi topografici per segnare con precisione il punto.

Fece tutte le operazioni programmate, compresa la foto con cui avrebbe documentato data e istante preciso della prima rilevazione e se ne tornò a casa soddisfatto, dopo avere gettato il seme per questa eccitante avventura nel mondo delle meridiane.

Per tutti i mesi successivi, ogni quindici giorni, Pautasso, con una precisione svizzera, continuò a piantare chiodi con la testa di un bel giallo canarino, nei punti in cui l'ombra dello stilo andava a cadere a mezzogiorno preciso. Ebbe solo una esitazione quando, a fine marzo, si passò all'ora estiva. “Adesso il mio orologio segna le 13, però sono le dodici. Come fa il sole a saperlo? Allora mi dico: Pautasso, pianta un bel chiodo con la testa di un colore diverso, che tanto ce li hai, un bel rosso papavero, che fa tanta allegria e serve a ricordarti che l'orologio segna un'ora in più .”

E così fece per aprile, maggio e via via fino ad ottobre,

A novembre riprese a piantare chiodi gialli e così fece anche a dicembre.

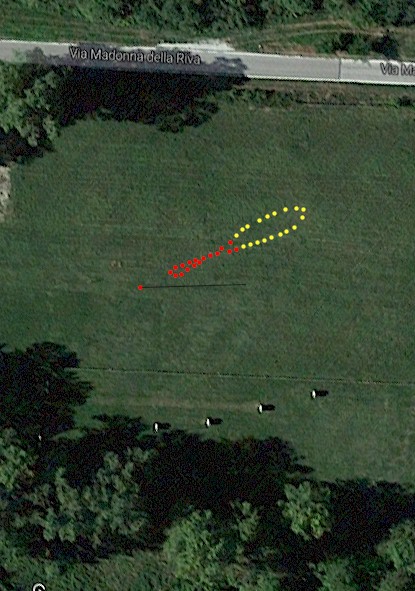
A Natale il simbolo dell'analemma, finalmente completato, metà giallo e metà rosso, appariva in tutta la sua arcana bellezza e Pautasso se ne compiacque molto. Scatto un'ultima fotografia e se la spedì al suo indirizzo mail: oreste.pautasso@gmail.com

Ne parlò con grande entusiasmo alla sorella e al cognato, che erano venuti a trovarlo proprio durante le feste di fine anno. Volle a tutti i costi portarli al cimitero, anche se loro non sembravano entusiasti, perché vedessero il suo capolavoro.

Il cognato Mattia osservò l'analemma e commentò. Questi chiodi non segnano proprio il mezzogiorno locale, perché l'ora del tuo orologio è quella del fuso orario nazionale, non quella di Cuneo.

Pautasso lo guardò sconcertato. “Ma ci sarà una differenza di poco conto, no?”

Mattia rispose semplicemente “basta fare due calcoli...”

Sarà in grado il nostro Pautasso di fare i calcoli a cui ha accennato Mattia? Lo scoprirete leggendo la prossima puntata! Intanto, se vi fa piacere, prima di continuare a leggere, potete dargli un aiuto ad’OK  e scriverlo nei commenti o inviarglielo per e-mail, lo farete felice!

 

Capitolo 2

Calcoli ? Pautasso si guardò intorno, come per cercare un aiuto da un inesistente compagno di banco, come ai tempi della scuola. Ma non c'era nessuno a suggerirgli una risposta, qualunque potesse essere.

“Non è che magari è colpa dell'orologio, questa differenza?” chiese solo per guadagnare tempo.

Mattia lo fissò divertito. “ Oreste, il tuo orologio va benone, la questione è un'altra...”

A salvare Pautasso arrivò il lamento della sorella Sofia. “Sentite un po', voi due, invece di discutere sugli orologi giusti o sbagliati, vedete di riportarmi a casa. Non voglio passare il Natale al cimitero, e poi queste scarpe mi fanno male ai piedi! Quando mai mi sono lasciata convincere dalla Nina che erano perfette per me!”

Arrivarono a casa. Mattia chiese “Hai mica una cartina d'Italia?” Pautasso si sentì preso in trappola e rispose precipitosamente “No che non ce l'ho, perché dovrei averla?” Mattia emise un breve sospiro e rispose “Con la cartina potrei farti vedere qual è il problema e quali sono i calcoli da fare...”.

L'idea che i calcoli non toccassero a lui rianimò Pautasso. “Vediamo un po', magari in qualche numero della Gazzetta dello Sport, dove parla del Giro, te la trovo.” Si mise a rovistare in un cumulo di vecchi giornali impilati su uno scaffale. “ Ecco! Giro d'Italia 2016, lo sapevo che era qui dentro..” e così dicendo porse al cognato la pagina con il disegno.

Mattia non perse un secondo, con una biro apparsa magicamente nelle sue mani, tracciò velocemente delle righe sulla cartina e la mostrò, tutto soddisfatto, al cognato.

“Ma perché me l'hai rigata tutta?”

“Adesso te lo spiego... Guarda !

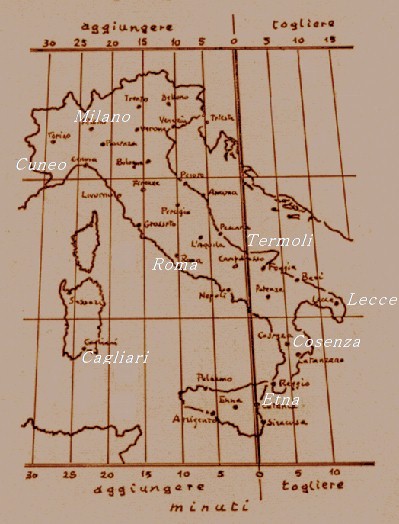
Quella linea più spessa, che dalla Sicilia, proprio dove c'è il vulcano Etna, sale verso il Gargano, passando “esattamente” per Termoli... ti ricordi vero di Termoli? Ci siamo stati nell'estate del 2012, un posto incantevole, un mare splendido, la cucina poi... Ma non divaghiamo. Innanzitutto dobbiamo distinguere il mezzogiorno solare, ovvero il momento in cui il Sole raggiunge il punto più alto sull’orizzonte, detto “culminazione”, dal mezzogiorno convenzionale, ovvero il momento in cui il Sole raggiunge il punto più alto nel meridiano centrale del fuso orario.

Quella linea che ho disegnato più spessa delle altre e che continua e continua, facendo il giro della Terra, è proprio il meridiano centrale del fuso orario del nostro Paese, e anche di altri, naturalmente. Quando diciamo che è mezzogiorno, per convenzione è mezzogiorno in tutta Italia, ma, dal punto di vista astronomico, questo è esatto solo per tutti i luoghi del paese che incontri lungo il meridiano centrale. Nelle altre città il mezzogiorno ovvero, ripeto, il momento in cui il Sole giunge nel punto più alto dell’orizzonte, deve ancora arrivare o è già passato. Chiaro? Devi pensare che tutte le città che si trovano sullo stesso meridiano vedono culminare il sole nello stesso istante. Guarda per esempio Milano e Cagliari, vedi?”

Pautasso ebbe la vaga sensazione di avere già sentito quel discorso in tempi remoti, chissà da chi.

“Vediamo, allora... se adesso il Sole è al culmine a Termoli, quando lo sarà a Cuneo?” chiese, prima che Mattia lo chiedesse a lui.”

“Innanzi tutto pensa che il cammino apparente che il Sole compie nel cielo va da Est verso Ovest. Quindi dal meridiano di Termoli si sposta in un certo tempo per arrivare a Cuneo. Quando è alla massima altezza a Cuneo, a Termoli si è già abbassato, quindi non è più mezzogiorno da un punto di vista astronomico ma è più tardi, proprio del tempo che il Sole ha impiegato per “spostarsi” sopra Cuneo.”

“E quanto è questo tempo, Mattia? Dimmelo...” Pautasso ricominciava a sentirsi in ansia per la questione dei calcoli.

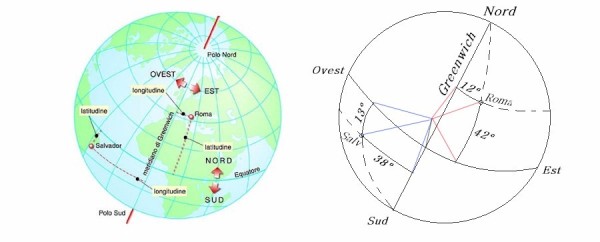
“Cominciamo col dire che ogni 4 minuti il Sole si sposta di un grado di longitudine, andando verso Ovest. Poi sappiamo che Termoli si trova a 15,00° Est, mentre Cuneo si trova a 7,53°... i gradi si contano sempre dal Meridiano di Greenwich... come sai.”

“Sì, sì, Greenwich... l'ho visto anche nel film di Robin Hood...”

Mattia fece finta di non aver sentito e continuò il suo ragionamento.

“Dunque, il calcolo è presto fatto: 15° – 7,53° = 7,47°. Adesso, se moltiplichi per 4' questa differenza, la convertirai nei minuti di ritardo da sommare all'ora ufficiale dell'orologio.”

Pautasso tirò fuori il cellulare e fece il conto: 7,47 x 4 schiacciò il tasto = e lesse con grande compunzione: 29,88. “Accidenti, mezz'ora di ritardo! Il Sole ci ha messo mezz'ora da Termoli a qui!”

Mattia sorrise rilassato.

“E’ proprio così, Oreste, puoi credermi! Ciò significa che quando in Italia gli orologi segnano mezzogiorno (quello convenzionale) a Cuneo manca ancora mezz’ora prima che il Sole raggiunga il punto più alto sull’orizzonte, quindi i cuneesi a mezzogiorno vedono il Sole alla stessa altezza a cui lo vedono i termolesi alle 11,30.”

“Mezz'ora...mi ricordo che noi ci avevamo messo otto ore di macchina, nel 2012...”

“Ma il Sole non segue le autostrade, Oreste, e non si sposta neppure come un aereo da un punto all'altro. Devi pensare solo ai gradi tra i due meridiani, la distanza sulla superficie terrestre dipende da dove ti trovi: se ti sposti lungo l'equatore, un grado di longitudine equivale 40.000 km / 360, cioè a ...”

“111 Km !” gridò Pautasso che, col cellulare in mano, si sentiva un leone.

“Già, 111 Km, anche facile da ricordare. Se invece ti muovi lungo il parallelo di Cuneo, che ha un raggio più piccolo, diciamo il 70% circa, allora...”

“7 Km! No! Aspetta... questi decimali! Un grado lungo il parallelo di Cuneo è quasi 78 Km!” strepitò Pautasso ormai incontenibile.

“E' così. Quindi lo spostamento di 7,47 ° corrisponde a poco più di 580 Km, percorsi in 30 minuti.”

Pautasso armeggiò ancora un attimo con il cellulare. Aveva un'espressione perplessa.

“Cosa stai calcolando?” domandò, incuriosito, Mattia.

“Ecco, mi sembra che, se per fare 580 Km il Sole ci mette mezz'ora, vuol dire che la sua velocità è di 1.160 Km all'ora. Ma io mi ricordo che la velocità della luce è 300.000 Km all'ora... Come mai va così piano?”

“Ma bene!” esclamò scandalizzato Mattia. “Innanzi tutto la velocità della luce è 300.000 Km AL SECONDO, e non all'ora. Poi, la velocità dello spostamento apparente del Sole non c'entra nulla con la velocità della luce che emette.”

“Ah ecco! Mi sembrava strano...”

“Va bene Oreste, adesso che hai capito (?) torniamo a vedere la cartina.

Ti ho disegnato le linee dei meridiani a intervalli di 5 minuti, in anticipo e in ritardo rispetto al centro del fuso orario.

Come vedi i conti tornano, la culminazione del sole a Cuneo è 30 minuti in ritardo rispetto al mezzogiorno convenzionale, è uno dei posti più ritardati, mentre, ad esempio Roma, è in ritardo di solo 10 minuti. Se poi guardi a Ovest di Termoli vedi che a Cosenza il Sole passa in anticipo di 5 minuti e a Lecce di una dozzina di minuti. C'è solo una cosa che non ti ho spiegato del tutto. Come si calcola la lunghezza del parallelo su cui si trova Cuneo.

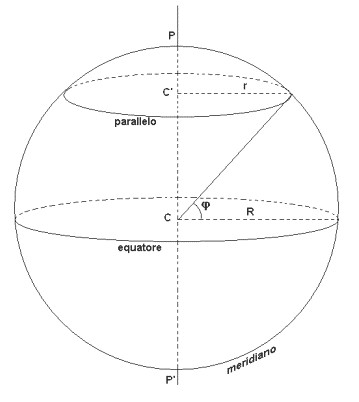
Perché ti ho detto che è circa il 70% della lunghezza dell'equatore...? Se guardi attentamente questa figura lo capirai. Considera che quell'angolo φ rappresenta la latitudine, che a Cuneo è circa 45°.”

Riuscirà Pautasso a sciogliere l’enigma? Continuate a leggere e lo scoprirete! Da parte sua ha promesso un premio speciale (davvero!) a quel lettore che riuscirà a dare la risposta giusta prima di lui e sarà ancora più speciale se riuscirà anche spiegare perché l'angolo di un grado viene coperto in un tempo di 4 minuti d'orologio. Se volete provare a vincere il premio, non dovete fare altro che dare la risposta nei commenti o per e-mail a oreste.pautasso@gmail.com

 

Capitolo 3

Ancora calcoli, accidenti, che idea balorda coinvolgere Mattia in quella faccenda! Pautasso aggrottò la fronte cercando di concentrarsi.

"Dunque, la circonferenza della Terra all'equatore è di 40.000 km, quindi il raggio è di 40.000/2π=6.366 Km. Dato che la latitudine di Cuneo è circa 45°... devo calcolare cos'è il raggio. Ma guarda un po'! Sulla calcolatrice c'è giusto questo tasto, con scritto “cos” proviamo...cos'è 45 ? Dice che è 0,707. Funziona ! È proprio il 70% ! Adesso basta moltiplicare 6.366 per questo 0,707 e poi per 2π e trovo la circonferenza del parallelo di Cuneo. Poi divido per 360° e ottengo 78 Km/° . Forte! Guarda un po'..."

“Oreste, guarda che “cos” non vuol dire “cos'è”, ma vuol dire “coseno”, cioè la funzione trigonometrica che ti dice quanto vale la proiezione del raggio del cerchio, inclinato di un certo angolo, rispetto l'asse orizzontale.”

“Quante storie ! Cos'è o Coseno, l'importante è che sia giusto !”

“Va bene, torniamo alla questione della rotazione terrestre. Hai capito perché un grado di rotazione si compie in 4 minuti d'orologio, vero?”

“Certamente Mattia, se in un giorno, che è di 24 ore, la Terra fa un giro completo, basta fare 24 x 60 minuti e trovo che in 1.440 minuti la Terra fa in tempo a girare 360° quindi, dividendo 1440 per 360° trovo in quanti minuti gira di un grado.”

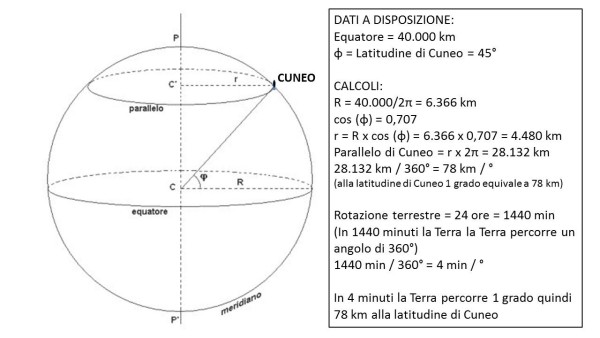
“Va bene, vedo che su questo non ci sono dubbi... Adesso che abbiamo capito che l'orologio non segna l'ora della culminazione locale per via della convenzione dei fusi orari, una convenzione e nulla più, come quella dell'ora estiva, dobbiamo capire se, per caso, non ci sia qualche altra cosa di “artificiale” nel modo in cui dividiamo le ore della giornata. Insomma domandiamoci fino a che punto il movimento della Terra rispetto al Sole, il suo riallinearsi giorno per giorno all'ora della culminazione, è rispecchiato dal movimento delle lancette degli orologi.”

“Domandiamocelo...” ripeté, con scarso entusiasmo, Pautasso, che pensava già di aver finito.

“Vi ho preparato il caffè...” Sofia era arrivata dalla cucina, portando un vassoio con le tazze fumanti, lo zucchero, il latte e un piattino colmo di Krumiri di Casale Monferrato. Pautasso accolse il suo arrivo con lo stesso sollievo che un pugile in difficoltà prova al suono del gong. Ma la pausa durò poco; bevuto il caffè, Mattia tornò all'attacco.

“Il tuo orologio, e anche il mio naturalmente, tutti gli orologi, “pensano” che la Terra ruoti su se stessa in un tempo sempre uguale. E fin qui niente da dire, anche se, a voler essere precisi, ci sono piccolissime variazioni per svariate interferenze di altri corpi celesti. Il punto è un altro: gli orologi credono anche che la Terra si muova attorno al Sole secondo un'orbita circolare, un cerchio al cui centro si trova, appunto, la nostra stella.”

“E no!” interruppe di botto Pautasso. “Questo non è vero. Lo sanno tutti: la Terra descrive un'orbita a forma di ellisse, il Sole non è nel centro ma in un punto vicino che si chiama fuoco, credo proprio per via del calore del Sole.”

“Già, vedo che lo sai...”

“Si, mi ricordo benissimo, l'ellisse è una curva comica, ce ne sono anche altre...”

“CONICA, Oreste, conica… come iperbole e parabola!! Valle a studiare QUI dalla lezione 14 alla 18. Ma andiamo avanti... Dunque, se l'orbita non è circolare, ci sarà una conseguenza pratica, no? Sarà ancora vero che il riallineamento con il Sole del nostro meridiano locale richiede sempre il medesimo tempo?”

“Credo di no, Mattia, altrimenti non mi avresti fatto questa domanda...”

“Infatti. Ma come avviene? Facciamo un disegnino dell'ellisse con i suoi fuochi, naturalmente dovremo esagerare un po' con l'eccentricità, che in realtà è molto più piccola, altrimenti vedremmo quasi un cerchio”.

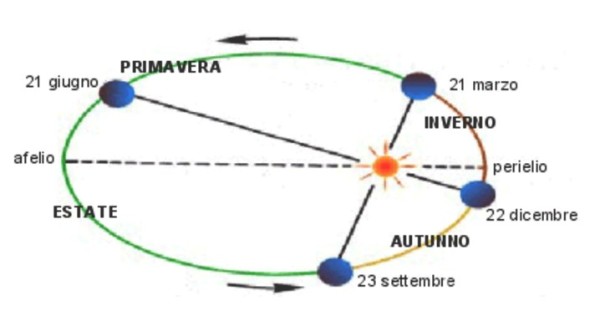
“Esageriamo... esageriamo”.

“Vedi bene, Oreste, che la distanza tra Terra e Sole cambia continuamente percorrendo l'orbita. Nel punto di minimo distano 147 milioni di Km e nel massimo 152.”

“Certo, e si capisce benissimo quando succede: se sono vicini fa caldo, se sono lontani fa freddo. Se l'orbita fosse circolare farebbe sempre tiepido.”

“No, Oreste, vedi... quando la Terra è vicina al Sole, si dice “al Perielio”, è proprio il momento più freddo dell'inverno. Questo perché l'inclinazione dell'asse terrestre in quel momento fa sì che i raggi del Sole arrivino più obliqui, l'irraggiamento è più debole, il giorno più corto e il calore accumulato nel mese precedente non è molto. Viceversa, quando il Sole, è più lontano, “all'Afelio”, succede il contrario, i raggi arrivano più verticali, le ore di luce sono molte e il calore già accumulato è notevole. E' proprio durante l'estate, che il Sole è più distante.”

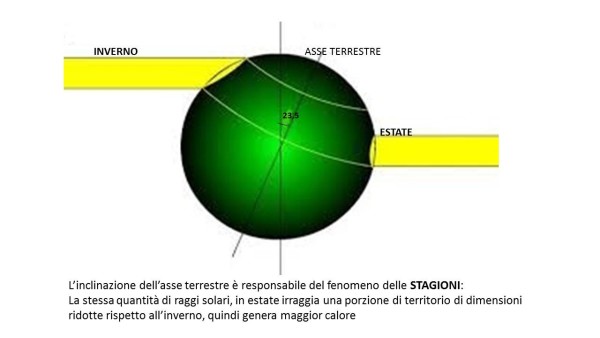
“Però quando da noi fa così caldo, nell'altro emisfero fa freddo ! Allora ?”

“E' proprio il fatto che ci sia questa differenza tra i due emisferi a farci capire che la distanza dal Sole non è rilevante, i due emisferi sono alla medesima distanza, eppure le situazioni sono opposte.”

Pautasso si rigirò sulla sedia, un po' a disagio. Questo fatto che la distanza dal Sole non contasse nulla non lo convinceva affatto. Intanto Mattia proseguiva, implacabile.

“La differenza tra le due distanze è di 5 milioni di km, mica poco... Vuol dire che il fuoco in cui si trova il Sole dista 2,5 milioni di Km dal centro. L'eccentricità pertanto vale 2,5/(152-2,5) = 0,0167 un numero davvero piccolo che, come dicevo, fa sembrare l'orbita circolare. Ma circolare non è.”

Pautasso deglutì a vuoto. Come poteva una ellisse così “rotonda” provocare differenze significative nella dinamica dei riallineamenti. Be' non è che avesse formulato la domanda proprio in questo modo, ma il senso era proprio quello.

“Dunque, per il momento non curiamoci del fatto che l'asse terrestre sia inclinato rispetto all'orbita, anche se lo è in realtà. Immaginiamo che l'asse sia ben verticale e che ci sia solo questa ellitticità a rendere diverso il modello da quello con cui ragionano gli orologi.

“Cosa pensi che vedremmo ogni giorno, osservando il cielo, in questa ipotesi?”

“Allora, per prima cosa il Sole sarebbe sempre alla stessa altezza ad ogni ora, in ogni giorno dell'anno, insomma non ci sarebbero le stagioni, e ogni notte durerebbe come il giorno...”

“Bravo Oreste! Continua...”

“Poi, vediamo, all'equatore farebbe un caldo bestia perché il Sole sarebbe sempre a picco sopra la testa per 12 ore al giorno, dalla mattina alla sera.”

“Giusto, e poi...”

“Che altro, non so... sei tu l'Astronomo della famiglia, Mattia! Io ne so molto menissimo di te.”

“Va bene, va bene… Allora ti dico che ci sarebbe anche una variazione del tempo del passaggio del Sole al meridiano locale perché, quando la Terra è al Perielio, (vicina al sole) si muove più velocemente, come se temesse, andando piano, di cadere sul Sole, e per questo in un giorno percorre un tratto di orbita più lungo della media. Così il meridiano si riallinea un po' in ritardo rispetto al tempo medio. Al contrario, quando...”

“Quando la Terra è lontana dal Sole, all'Afelio correrà di meno, l'angolo descritto in un giorno sarà più piccolo della media e la Terra dovrà “recuperare” di meno, così il riallineamento si realizzerà in un tempo più breve di quello medio.”

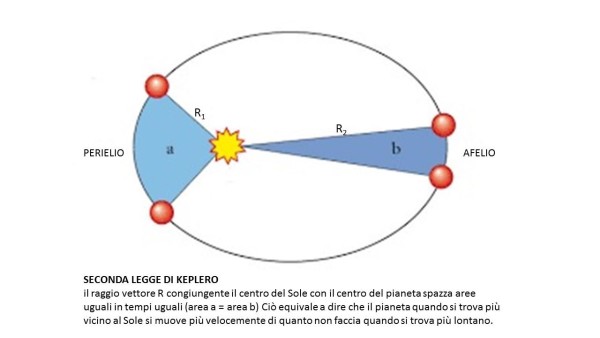
Mattia gli lanciò un'occhiata, sorpreso da quella insolita e inattesa eloquenza.

“Benissimo quindi, riassumendo, gli orologi dividono i 360 gradi, percorsi in un anno, in archi tutti uguali a 360°/365 giorni. In realtà, invece, gli archi sono tutti diversi e i loro valori si susseguono alternando ritardi e anticipi, tranne che in quei due giorni in cui non c'è né ritardo né anticipo.”

Pautasso si alzò e si diede una stiracchiata.

“Facciamo una pausa nee, Matteo? Mi sento un po' stanchino...”

“Va bene Oreste, Più tardi cercheremo di disegnare la posizione del Sole mentre transita al meridiano, a seconda del punto dell'orbita in cui, in quel giorno, si trova la Terra, sia secondo l'opinione degli orologi, che credono che l'orbita sia circolare, sia nella ipotesi che abbiamo appena discusso, di un'orbita ellittica.”

“Hai capito, vero, Oreste? La domanda a cui rispondere è questa ...

"Se da inizio anno, ogni 90 giorni, fotografassimo a mezzogiorno la zona di cielo centrata sul meridiano locale, memorizzando la posizione del sole al suo passaggio, quale immagine otterremmo?”

Egregissimo lettore, ti scongiuro di non lasciarmi solo nelle mani del cognato. Se avessi saputo che prendeva questa brutta piega stavo taciturno. Comunque ormai la frittata è fatta, come diciamo qui a Cuneo. Se mi puoi dare una mano tu, o magari hai un nipote che studia queste cose qui....

Con ossequiosi ringraziamenti,

oreste.pautasso@gmail.com

P.S. Ho firmato con la mia mail di Cuneo, così, se preferisci, puoi dare un suggerimento segreto.

 

Capitolo 4

Quella sera non se ne fece nulla. Quando Mattia, dopo cena, propose di riprendere il discorso, la risposta di Pautasso fu: “Mi è venuto un mal di testa, ma un mal di testa, che è meglio che me ne vada subito a letto...” E così fece.

Solo la mattina seguente, dopo colazione, Mattià tornò alla carica.

“Se te la senti, possiamo riprendere il discorso di ieri. Sai, ho pensato di rifare tutto il ragionamento in un modo che porti facilmente a rispondere alla domanda su cui ci eravamo fermati.”

Pautasso sentì un vago formicolio dietro le orecchie, mentre udiva la sua voce che rispondeva alla proposta. “Benissimo, sono pronto, adesso sì che comincia il bello!” Ma in cuor suo provava una sensazione di smarrimento all'idea di dover riprendere il combattimento con quei capricciosi movimenti terrestri: un po' in ritardo, un po' in anticipo, mai regolari, per i quali Mattia provava tanto entusiasmo.

“Oggi però vedremo le cose dal nostro punto di vista, da qui dove ci troviamo...”

“A Cuneo !”

“Sì, Oreste, a Cuneo. Dicevo, se guardiamo verso sud, lì c'è il nostro meridiano, è lì che il Sole passa a mezzogiorno.”

“Quando a Termoli sono le 12 e 30...”

“Certo, l'orologio segna le 12 e 30... Devi pensare che quando guardiamo il Sole e lo vediamo muoversi, il suo movimento è la combinazione di due diversi movimenti. Il Sole si sposta verso est, di circa un grado al giorno, in realtà in certi periodo è più veloce e in altri è più lento. Poi c'è il movimento dovuto alla rotazione della Terra che in un giorno fa un giro su se stessa.”

Pautasso si era fatto attento e voleva dire la sua.

“Quindi il movimento della Terra è molto più veloce di quello del Sole e questo è il motivo per cui vediamo il Sole andare a Ovest”

Mattia proseguì, stava arrivando il punto cruciale.

“Certo, ma ricordiamoci che il Sole ha una velocità variabile...Ecco, vediamo questo disegno che ho fatto per noi, ieri sera:”

 

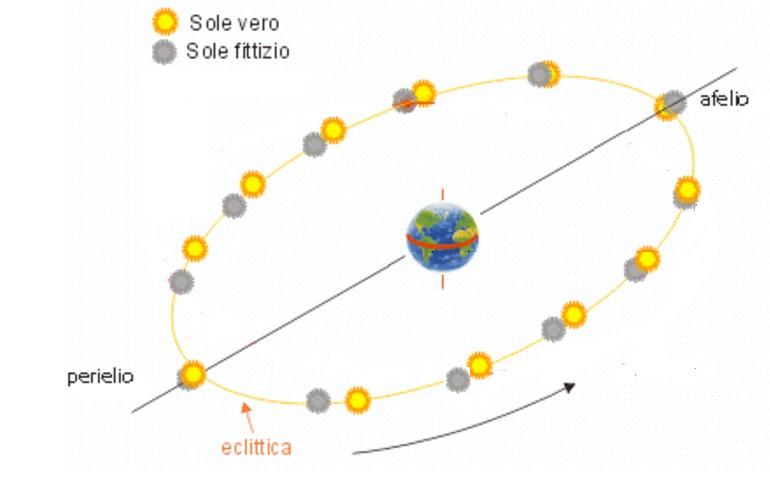
Facciamo finta che sull'orbita ellittica ci siano due Soli: uno è quello vero che si muove più velocemente quando è più vicino al Perielio e più lentamente quando è nel punto opposto, all'Afelio.

L'altro Sole, finto, che vedi rappresentato in grigio, si muove con una velocità invariabile, qualunque sia la sua posizione. Misureremo il ritardo o l'anticipo del Sole vero su questo Sole finto, che ragiona come gli orologi.

“Forte!” A Pautasso brillavano gli occhi.

“Vediamo un po': i due Soli partono insieme, Il Sole vero, vedendo che il perielio è proprio lì vicino si mette a correre e distacca il Sole finto, che procede al suo passo costante. Ora dimmi, come vediamo passare i due Soli dal nostro punto di osservazione locale?”

“Qui, a Cuneo, siccome la Terra gira anche lei in senso antiorario, vediamo passare prima il Sole finto e, con un certo ritardo, il Sole vero.”

“Bene, questa situazione si ripete ogni giorno, ma via via che il perielio è più lontano, il Sole vero rallenta, come sappiamo, finchè si metterà al passo con il Sole finto che, imperturbabilmente, non ha mai cambiato ritmo.”

“E questo lo possiamo capire dal fatto che ogni giorno il ritardo del passaggio del Sole vero su quello finto si riduce.”

“Appunto, e dove si ritroveranno appaiati, secondo te?”

“Ma all'afelio, no?”

“Proprio all'afelio, ai primi di luglio, quando non avremo alcun ritardo nel passaggio del Sole.”

“E adesso, Mattia cosa succede?”

”Succede che il Sole vero, vedendo che l'afelio è vicino se la prende comoda e si lascia superare dal Sole finto. Quello lì l'afelio non lo guarda neanche!”

“Eh sì, Oreste, come vedi nella figura, in questo periodo il Sole finto, con il suo passo costante, cadenzato, prende un bel vantaggio, mentre il Sole vero resta indietro e dal nostro punto di osservazione lo vediamo passare prima di quello finto”

“Vero, ma ogni giorno riduce un po' questo distacco, perché l'afelio è più lontano e il perielio è più vicino!”

“Sì, infatti, quando il perielio è più vicino, il Sole vero riprende a correre, il suo ritmo accelera e supera quello del Sole finto finché, in un finale travolgente, lo raggiunge proprio sul traguardo. A questo punto sono di nuovo pari e li vediamo passare insieme.

“Quasi quasi non ci credo, ma ho capito tutto!” Pautasso si era davvero entusiasmato.”Non vedo l'ora di andare al CAC (Circolo Archeofili di Cuneo, ndr) per raccontare questa meraviglia al presidente.”

“Adesso che abbiamo visto tutto quanto, non ci resta che rispondere alla domanda di ieri sera...”

Se da inizio anno, ogni 90 giorni, fotografassimo a mezzogiorno la zona di cielo centrata sul meridiano locale, memorizzando la posizione del sole al suo passaggio, quali immagini otterremmo?

Aggiungiamo il particolare che, essendo a Cuneo, il “mezzogiorno” corrisponde alle ore 12.30. Inoltre, per tutto il periodo in cui è in vigore l'ora legale, corrisponderà alle 13.30.

Pautasso prese la matita che era sul tavolo e fece questo disegno...

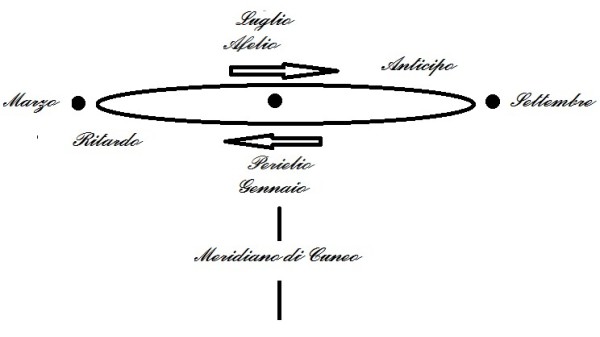
Siete d'accordo con lui?

Se non siete d'accordo diteci per quale motivo.

Le ipotesi su cui Mattia e Oreste hanno ragionato sono di una Terra con il piano equatoriale complanare al piano dell'eclittica, in altre parole con l'asse di rotazione perpendicolare al piano dell'orbita di forma ellittica.

 

Capitolo 5

Mattia osservò il disegno tracciato da Pautasso con evidente soddisfazione.

“Benissimo, Oreste, questo diagramma rappresenta proprio gli anticipi e i ritardi, che ciclicamente si verificano esclusivamente a causa della ellitticità dell'orbita. Infatti se l’orbita fosse circolare, la Terra si muoverebbe di moto circolare uniforme e gli orologi andrebbero d’amore e d’accordo con il Sole vero. Se rappresentiamo questi anticipi e ritardi con un grafico, mese dopo mese, abbiamo una curva che parte da zero, raggiunge un massimo, ripassa da zero e raggiunge un minimo e, infine, torna a zero chiudendo il ciclo. In pratica è una sinusoide.”

Pautasso annuì. “Eh sì, la sinusoide è una brutta bestia, io l'ho avuta da piccolo, un mal di testa, ma un mal di testa...”

“Oreste, non ho detto sinusite, ma sinusoide. E' una curva che sembra una S sdraiata, parte da zero arriva al massimo, poi scende, ripassa da zero, quindi tocca il minimo e torna a zero. Guarda, te la disegno...”

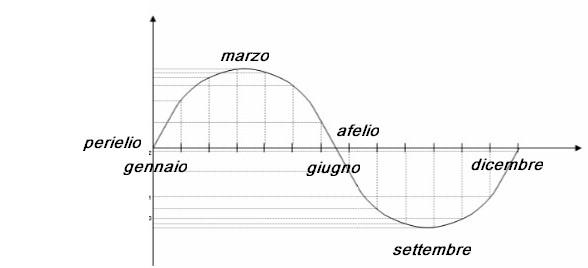
“Ho capito, una S sdraiata, però sarebbe più una Z sdraiata, e “arrotondata”, secondo me.”

“Va bene, andiamo avanti. Gli scostamenti massimi nella culminazione sono dell'ordine di alcuni minuti. Da da gennaio a marzo i ritardi si accumulano fino ad un massimo di 7 minuti a fine marzo. Poi iniziano i giorni con anticipi che riducono il ritardo raggiunto e, a fine giugno, lo riportano a zero. Gli anticipi proseguono ad accumularsi fino a settembre, raggiungendo il massimo di 7 minuti. Da questo punto in poi tornano in gioco i ritardi che, un po' per volta, fanno diminuire sempre di più l'anticipo, fino ad annullarlo alla chiusura del ciclo.”

“Ma come facciamo a “vedere” la curva? Fino ad ora abbiamo solo i ritardi e gli anticipi...”

“Certo, fin qui abbiamo analizzato gli effetti di un’orbita ellittica e di un asse terrestre perpendicolare al piano orbitale. Per questo motivo l'altezza del Sole è sempre la stessa. Ma sappiamo che l’asse terrestre è inclinato rispetto al piano orbitale, ricordi? E’ per questo che abbiamo le stagioni ed è per questo che nella stagione invernale il sole è più basso sull’orizzonte e in quella estiva è più alto. Aggiungiamo questa informazione al diagramma che avevi tracciato per indicare gli spostamenti in anticipo e in ritardo e, invece di una semplice linea orizzontale, vedremo una curva a forma di ellisse. “

Mattia disegnò la curva qui sotto.

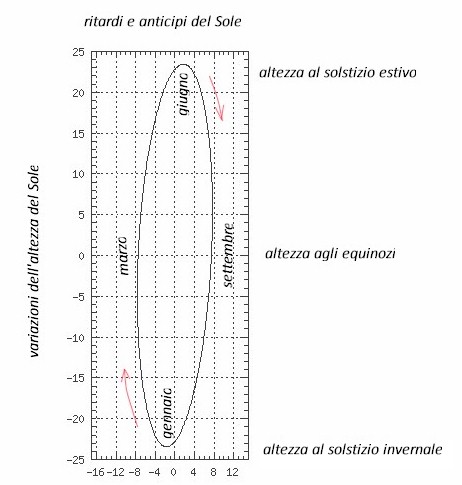
“Non abbiamo ancora finito, Oreste, la realtà è più complicata e adesso viene la parte più difficile...”

Il sorriso che fino a quel momento aveva illuminato la faccia di Pautasso si smorzò. Ma come, sembrava tutto risolto... Aveva anche capito al volo l'ultimo disegno di Mattia, con quella ellisse birbacciona (certo che queste ellissi non finiscono mai...). E, proprio adesso, salta fuori che la parte difficile deve ancora cominciare, oh basta là...

“Scusa Mattia ma non basta così? Cosa c'è ancora da dire?”

“Adesso faremo il contrario, cioè studieremo il caso di un'orbita circolare, con il Sole nel centro, e vedremo come influirà, sull'istante di culminazione, il fatto che l'asse terrestre risulti inclinato come è in realtà.”

“Ma non l'abbiamo appena visto..?”

“Solo in parte, Oreste, solo in parte...”

“Oh basta là!”

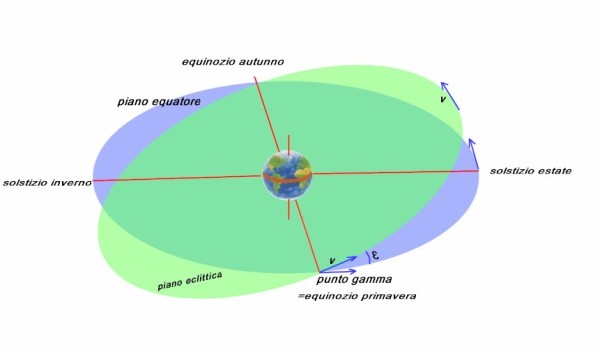
“Dai, Oreste ! Abbi ancora un po' di pazienza... Ecco, guarda questa figura, rappresenta la situazione dal punto di vista della Terra (al centro). Il Sole è visto muoversi sul piano della eclittica (verde), che non coincide con il piano equatoriale (azzurro), data l'inclinazione dell'asse terrestre.

Sul piano dell'eclittica il movimento del Sole descrive un cerchio (abbiamo detto che non teniamo conto della eccentricità ). Ma sul piano dell'equatore, che è inclinato di 23,5° questo cerchio appare come una ellisse”

Pautasso alzò gli occhi al cielo.”Ancora una ellisse !...”

“”Già, nota anche che i due piani si intersecano lungo una retta che passa per il centro della Terra. Vedi, in primo piano, quel “punto Gamma” , che coincide con l'equinozio di primavera? Ebbene è proprio da quel punto che incominciamo a valutare come il Sole si sposta apparentemente lungo l'ellisse nel piano equatoriale.”

“Però in realtà il Sole gira con una velocità costante lungo l'orbita circolare sul piano verde...”

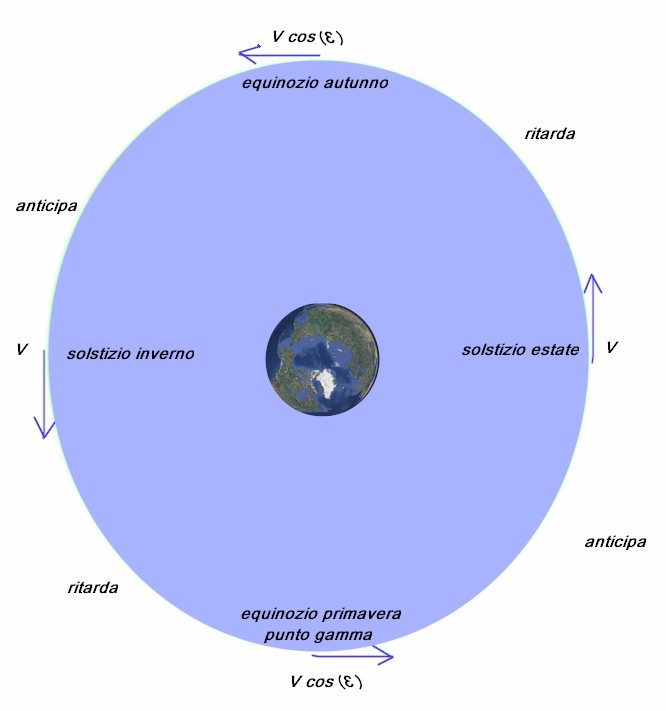
“Vediamo meglio, in pianta, la proiezione dell'orbita sul piano equatoriale, quello azzurro. Nota che siamo al di sopra del polo Nord terrestre” Disse Mattia. “Ebbene, mentre il movimento circolare, regolare, si svolge sul piano verde, contemporaneamente il Sole, che vediamo sul piano equatoriale qui sopra, azzurro, si muove lungo l'orbita ellittica. Quando i due piani si intersecano (agli equinozi) la proiezione della velocità sul piano equatoriale sarà V cos(ε), dove ε vale 23,5°, al suo valore minimo. Invece, al passaggio ai solstizi, l'orientamento della velocità proiettata sul piano equatoriale ed il suo valore (massimo), coincideranno con quelli sul piano dell'eclittica.”

“Ma allora, Mattia, la velocità della proiezione del Sole sul piano equatoriale non è mai superiore a quella del Sole? Se è così come avviene il recupero dei ritardi?”

“Bravissimo Oreste! Infatti ci resta ancora una cosa da dire... La velocità di cui abbiamo parlato è quella tangenziale e non quella angolare! Se le due velocità tangenziali sull'eclittica e sulla sua proiezione sono uguali, come avviene ai solstizi, la velocità angolare sarà superiore sul piano della proiezione, perché in quei punti, dove l'ellisse è più “schiacciata” il raggio dell'orbita è più piccolo e, a parità di velocità tangenziale, la velocità angolare sarà più grande.

* (vedi nota a fine pagina)

"Allora, Mattia, appena il Sole “proiettato” parte da questo punto gamma e si dirige verso il punto del solstizio estivo, comincerà a muoversi lentamente e poi andrà accelerando. Quindi all'inizio vedrò il sole "vero" in anticipo ma poi l'anticipo si ridurrà e al solstizio si sarà annullato.”

“Proprio così , Oreste. Superato poi  il punto del solstizio, alla massima velocità,  il sole "proiettato" comincerà a rallentare. Quindi, osservando il sole "vero",  noteremo  un ritardo iniziale che poi calerà fino ad annullarsi all'equinozio di autunno, diametralmente opposto al punto gamma. E così via.”

 

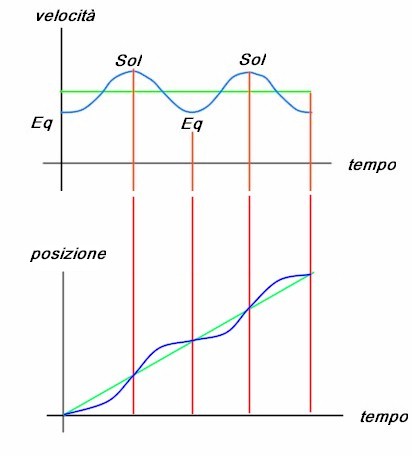
“Allora ci saranno quattro punti in cui non abbiamo né ritardo né anticipo? Cioè gli equinozi e i solstizi?”

“Precisamente, ci saranno due massimi e due minimi, due cicli completi della sinusoide, Solo ai solstizi e agli equinozi non avremo ritardi o anticipi.

“Ho capito, la sinusoide dell'eccentricità, la prima che abbiamo disegnato, ovvero quella generata dalla forma ellittica dell’orbita terrestre, è semplice, questa invece è doppia.”

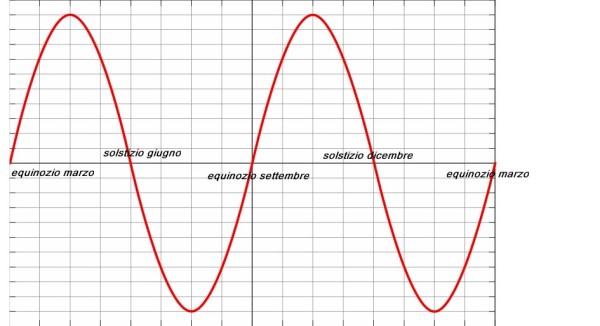
“E' proprio così, due cicli completi”

“E il disegno della posizione del Sole, come lo faccio, adesso?”

“Oh, Oreste, per questo devi solo abbinare ad ogni giorno i suoi due valori di altezza sull'orizzonte e di anticipo o ritardo, dovuto solo all'effetto dell'inclinazione dell'asse, alla sua obliquità. Ti posso ancora dire che nei momenti di maggiore scostamento il Sole ritarda o anticipa di circa 10 minuti.”

“Cari amici lettori, cosa posso dirvi.... Aiuto!!! Il cognato mi chiede di fare un disegno, come quell'altro di ieri, ma che tenga conto che in inverno il sole è basso, che in estate è alto che in primavera e autunno è giusto. In più bisogna pensare che ritarda tanto o anticipa tanto tra equinozi e solstizi ma poi, proprio in quei momenti lì, è zero ! Ma, insomma, cosa pretende? Aiutatemi voi che a me è tornato il mal di testa come quando avevo la sinusoide!”

 

Capitolo 6

 

 

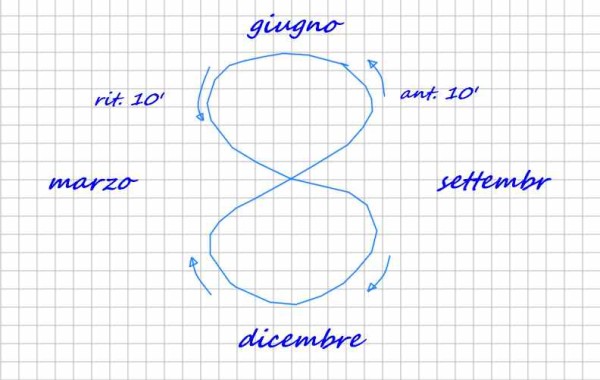
La luce del mattino entrava dall'ampia finestra del soggiorno, illuminando il disegno su carta a quadretti che Pautasso aveva tracciato con il pennarello blu, quello portafortuna, che il CAC distribuiva alle conferenze.

Mattia stava osservando il disegno, mentre Sofia, dopo aver portato in tavola la colazione, si dava da fare attorno alla stella di Natale che cominciava già a perdere qualche foglia.

“Forse l'ho bagnata troppo? O troppo poco? Questa pianta, non si sa mai come trattarla! Ieri sera le ho dato un bicchiere d'acqua...”

“Anche tu? Le chiese Mattia, perché l'ho bagnata anch'io...”

“Come, l'avete bagnata anche voi?! Ma se ho detto che ci pensavo io...” interloquì Pautasso che era appena entrato in cucina.”

Si guardarono e nessuno disse niente, neanche la pianta.

“Va bene, vediamo qui... Allora sei riuscito a fare il disegno che dicevamo. Vedi che non era poi così difficile?” Disse allegramente Mattia.

“Eh sì, caro cognato, questo disegno dell'altalena mi ha fatto penare un bel po', ma alla fine ho capito come dovevo fare”.

“Analemma, Oreste, analemma, non altalena. Va bene che è una parola greca....”

“Insomma, perché non lo chiamano “otto”... Io non capisco questa mania dei nomi stranieri.”

“In ogni caso il disegno va bene, ma come già avrai capito non è quello che corrisponde alla figura che hai costruito nel campo, perché questa tiene conto solo di una delle due cause, l'effetto della inclinazione dell'asse.”

“Quindi la faccenda non è chiusa?”

“Manca poco, Oreste, dobbiamo solo mettere insieme i risultati che abbiamo ottenuto fino ad ora.

Seguimi...”

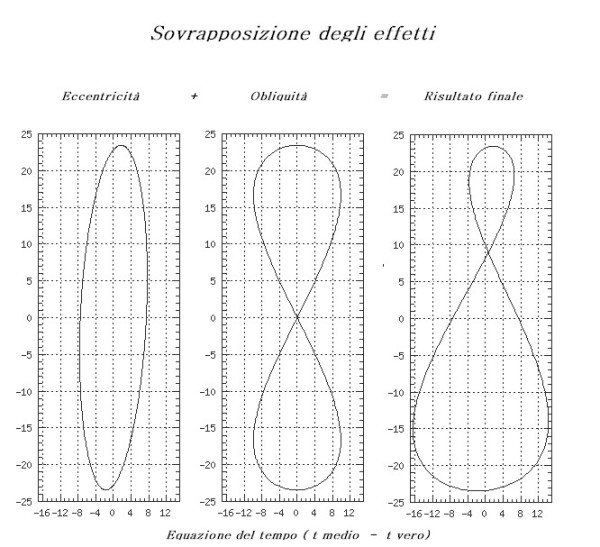
“Per un certo giorno conosciamo il valore dello scostamento dell'altezza del Sole al momento in cui passa al meridiano, rispetto alla linea dell'equatore celeste preso come riferimento. Quindi abbiamo la coordinata verticale.

Per determinare l'altra coordinata, quella orizzontale, basterà sommare gli effetti dei ritardi e degli anticipi causati da eccentricità e obliquità. Avremo così individuato il punto cercato sul nostro diagramma”

“Già, e ripetendo per i vari giorni questa operazione, troviamo gli altri punti...” Soggiunse pensieroso Pautasso.

“Ecco qui, riprese Mattia, vediamo… ad esempio, quando la declinazione è -20° rispetto alla linea dell'equatore celeste, l'effetto della eccentricità è di ritardare circa 5' e l'effetto della obliquità è di ritardare 9', quindi riporto sul diagramma complessivo 5+9=14 minuti di ritardo. Segniamo questi punti con un pallino rosso.

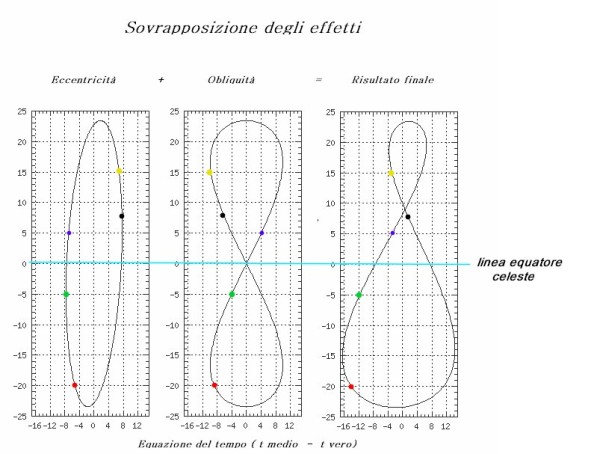
Ora saliamo lungo le curve fino ad un punto in cui la deviazione dalla linea dell'equatore sia, diciamo, -5°. L'eccentricità fa ritardare di 8' e l'obliquità di 4', totale 12' di ritardo. Questo lo vediamo osservando i pallini verdi. Con valori di declinazione al di sopra della linea dell'equatore, come +5° (e questo lo vediamo osservando i pallini blu) troviamo un ritardo di 7' per l'eccentricità e, questa volta, un anticipo per l'obliquità pari a 4'. Così il risultato complessivo sarà un ritardo di 3'.

Oltrepassato il punto di massima elevazione, le curve iniziano il tratto di ritorno, scendendo. Quando ripassano sulla linea a +15, vediamo i pallini colorati in giallo: per l'eccentricità ora abbiamo un anticipo di 7', mentre per l'obliquità abbiamo un ritardo di 10'. Conclusione: sovrapponendo i due effetti otteniamo il ritardo di 3'.

Ti faccio l'ultimo esempio, perché credo che a questo punto non avrai più dubbi... I pallini neri ci dicono che, quando le due curve scendendo, raggiungono l'elevazione + 8° sopra l'equatore, l'effetto della eccentricità è di causare un anticipo di 7' mentre l'effetto della obliquità è di causare un ritardo di 6'. Quindi l'effetto combinato è un ritardo di 2'.”

“Già! E ripetendo per i vari giorni questa operazione, troviamo gli altri punti...” Soggiunse pensieroso Pautasso “E quando li avremo individuati tutti, avremo disegnato l’ANALEMMA, ovvero quella curva geometrica a forma di otto allungato, che descrive la posizione del Sole nei diversi giorni dell'anno, alla stessa ora e nella stessa località.” Esclamò Mattia.

“Adesso ho proprio capito bene, Mattia, però, questo fatto del ciclo che si ripete due volte ad ogni giro non mi è del tutto chiaro... Se l'asse terrestre fosse verticale non ci sarebbe per niente questa oscillazione, ma se fosse orizzontale...?”

“Sai che c'è un pianeta che presenta proprio questa caratteristica? E' Urano, il penultimo pianeta del sistema solare, molto lontano, quasi 20 volte la distanza Terra-Sole. Come pensi che sarà il suo analemma? ”

Pautasso si concentrò, una ruga verticale apparve tra le sue sopracciglia.

“Se l'asse del pianeta è parallelo al piano dell'orbita... quando si trova allineato con il Sole uno dei due poli è totalmente illuminato. I raggi lo colpiscono perpendicolarmente e dovrebbe fare molto caldo, in quel momento, invece all'equatore i raggi arrivano molto radenti. L'emisfero di quel polo sarebbe illuminato per 24 ore mentre nell'emisfero opposto sarebbe totalmente buio.”

“Bene, vai avanti, cosa succederebbe poi?”

“Dopo un po' di giorni l'asse non punta più verso il Sole e quel polo non riceve più i raggi proprio verticali come prima, l'emisfero non sarà più totalmente illuminato e il Sole, invece di occupare sempre lo stesso punto descriverà, nel corso delle 24 ore, un cerchio in alto nel cielo, piccolo se siamo al polo, più grande andando verso l'equatore. All'equatore i raggi saranno meno radenti e ci saranno 12 ore di luce e 12 ore di buio (anche se un po' di luce arriverà ancora finché il sole non è sceso troppo sotto l'orizzonte)”

“E nell'emisfero opposto?” incalzò Mattia visibilmente soddisfatto.

“Nell'emisfero opposto, vicino all'equatore, ci saranno 12 ore di luce con il sole basso sull'orizzonte, ma la luce andrà aumentando, man mano che il Sole salirà nei giorni successivi. A un certo punto il polo che prima era illuminato, comincerà ad essere in ombra qualche ora al giorno, finché, dopo avere percorso un quarto del cerchio dell'orbita, il Sole sarà perpendicolare all'equatore e i suoi raggi arriveranno radenti ai due poli. E' una situazione in cui tutti hanno 12 ore di luce e 12 ore di buio.”

Pautasso respirò profondamente.

“Perfetto, poi tutto si ripete simmetricamente nei tre mesi successivi, alla fine dei quali il polo che inizialmente era al buio si ritrova in piena luce. Negli altri sei mesi quindi la situazione si ribalterà.”

“Insomma, Mattia, ci sarebbero dei momenti di grandissimo caldo e dei momenti di grandissimo freddo, altro che stagioni e mezze stagioni... Ma a parte questo, come sarebbe l'analemma?”

“Ebbene, se la Terra avesse un asse inclinato di 90°, invece di avere questa oscillazione di 23,5°gradi in più o in meno nella declinazione, avremmo una oscillazione molto più ampia, di 90°, quindi tutta la volta visibile.

Per quanto riguarda gli anticipi e i ritardi, invece di 10 minuti, per effetto di questa estrema inclinazione, arriveremmo ad avere 39 minuti di ritardo o di anticipo del passaggio al meridiano.

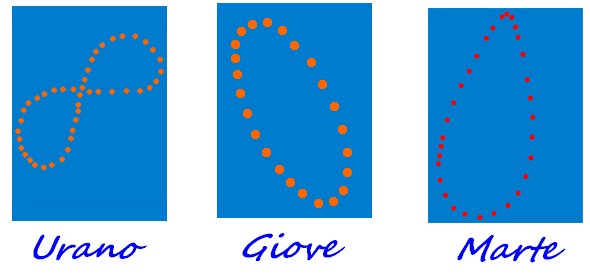
La curva formerebbe comunque un otto, di forma e proporzioni diverse, come accade del resto anche per Urano.”

“Quindi l'analemma è sempre una specie di otto? Per tutti i pianeti?”

“No, dipende da qual è l'effetto prevalente. Per esempio nel caso di Giove, che ha un'orbita più eccentrica della Terra e un asse di rotazione quasi perpendicolare al piano, prevale l'effetto della eccentricità e l'analemma ha la forma di un'ellisse...”

“Ancora un'altra ellisse... oh basta là!”

“Invece, nel caso di Marte, che ha un asse di rotazione inclinato poco più di quello terrestre, ma una eccentricità molto superiore, l'ellisse si restringe e assume la forma di una goccia, come fosse la parte inferiore dell'“otto”, senza l'anello superiore.”

“Bene! Adesso so proprio tutto...”

“Eh, Oreste, non farti illusioni, abbiamo solo sfiorato questo argomento, ci sarebbe ben altro da dire e da approfondire, ma diciamo che è già qualcosa. Adesso hai almeno un'idea del motivo per cui si forma quella strana figura, niente di più.”

“Si Mattia, ti devo proprio ringraziare. Sai cosa facciamo adesso? Diciamo a Sofia di preparare un buon caffè extra per tutti e poi spiego anche a lei questa cosa dell'analemma, scommetto che non ne sa niente.”

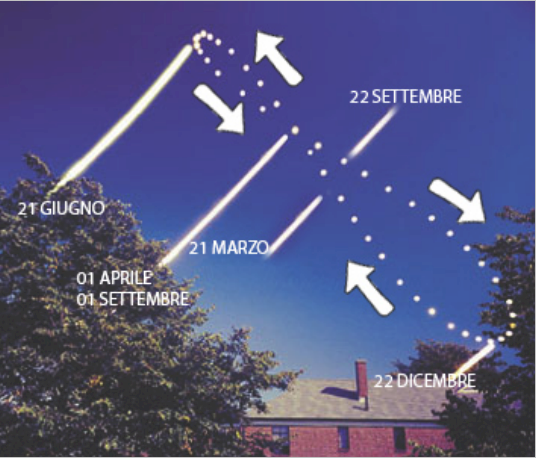
Qui sotto potete vedere immagini che abili fotografi hanno realizzato, con ammirevole costanza, sovrapponendo gli scatti eseguiti nel corso di un intero anno delle posizioni del sole.

L'ultima immagine è la simulazione di come apparirebbe l'analemma dalla superficie di Marte.

 

 

Cari lettori, a questo punto starete pensando che la storia è conclusa, vero?

Invece no, c'è ancora una piccola sorpresa che vi attende, come in quei film che poi salta fuori all'ultimo momento che l'assassino è un altro, che sembrava una brava persona.

Allora vi dico: seguitemi nel backstage del teatro, non mancate nee?

 

Capitolo 7

(ovvero il backstage o, meglio, il bechsteig, come direbbe Oreste)

Il giorno di carnevale, sotto un sole splendente, la piazza di Santa Maria Maggiore di Mondovì era piena di turisti. Tra la folla c'era anche Oreste Pautasso che, armato di cellulare, stava fotografando da ogni possibile punto di vista l'artistica meridiana che abbelliva la facciata del palazzo dei Conti di San Quintino.

“Che splendida facciata, guarda, Maria, c'è anche una meridiana...”Il distinto signore, a due passi da Pautasso, stava indicando con ammirata meraviglia alla sua compagna il quadrante solare che spiccava al centro dell'edificio, proprio sopra la balconata.

“Oh, sì è proprio bellissima. Ma come mai hanno disegnato quel brutto otto? Non saranno mica stati dei vandali eh?”

“Permettete? Il mio nome è Pautasso, Oreste Pautasso... Adesso vi spiego. Avete presente che la Terra gira, neh? Ebbene, dovete sapere...”

Mezz'ora più tardi, al centro del nutrito capannello che gli si era formato intorno, Pautasso concludeva la sua spiegazione tra gli appalusi degli astanti.

“... E così ora l'analemma non avrà più misteri per voi. Se poi qualcuno fosse interessato a portarsi a casa qualcosa di più di un fugace ricordo... avrei qui qualche opuscolo che ho fatto stampare e sarei lieto di consegnare a chi è interessato, chiedendo in cambio solo un piccolo contributo per le spese di stampa, diciamo 7 Euri... Oppure, se preferite, con 2 Euri lo potete scaricare in formato ebook da Amazon.”

“Faccia un po' vedere... professore”

“Per carità, non sono professore, sono solo un... simpatizzante, non mi attribuisca un titolo che non mi spetta.”

“Va bene, signor simpatizzante, ma vediamo questo opuscolo...”

“Ecco qua, sono vari esempi di analemmi che ho voluto studiare. Alcuni casi sono proprio esagerati, altri, invece, sono molto vicini alla realtà. C'è di tutto...” E così dicendo, Pautasso sciorinò un pieghevole ampiamente illustrato che noi stessi abbiamo acquistato per potervelo mostrare (per fortuna a noi ha fatto il 20% di sconto in quanto affiliati ad un noto sito di divulgazione astronomica!).

*************************************************

ALCUNI CASI NOTEVOLI DI ANALEMMI – A cura di Oreste Pautasso - Cuneo

Premessa

La figura un po' misteriosa dell'analemma, che sovente correda le belle meridiane dipinte sulle facciate di antichi palazzi o di chiese o, talvolta, anche di semplici case dei nostri borghi, non manca mai di suscitare la curiosità del passante che si sofferma davanti a questo simbolo, chiedendosi quale sia il suo significato e il suo utilizzo.

Potremmo dire che l'analemma è una porta di comunicazione tra due mondi, tra due visioni di uno stesso fenomeno. Un mondo è quello artificiale degli orologi che scandiscono meccanicamente (o elettronicamente) lo scorrere del tempo, secondo un ritmo costante, immutabile; l'altro è quello delle leggi naturali che hanno loro dinamiche, la cui armonia è stata svelata da immensi pensatori che si sono succeduti nel corso dei secoli, riuscendo a far luce sulle regole che governano i moti dei corpi celesti, raggiungendo, passo dopo passo, una comprensione sempre più profonda.

Ebbene, l'orologio che hai al polso, gentile turista, è convinto che la Terra si muova secondo una musica banale, una monocorde e ripetitiva battuta, istante dopo istante. L'orbita su cui la Terra conduce il suo moto è pensata perfettamente circolare, la velocità di percorrenza, assolutamente costante, il piano del suo equatore, giacente sul piano dell'orbita stessa e l'asse, l'asse di rotazione, assolutamente perpendicolare all’eclittica.

Ora, ben più ricca è l'armonia del Creato, come le coreografie di un balletto classico sono più complesse di un saltarello popolare. L'orbita della Terra è ellittica, il Sole non è nel centro, ma in uno dei fuochi, la velocità del nostro pianeta, nel suo moto di rivoluzione, è variabile da istante a istante, l'inclinazione tra piano equatoriale e piano dell'eclittica determina una mutevolezza nella elevazione del sole sull'orizzonte. In ogni momento, i raggi del Sole lambiscono la superficie terrestre con un moto a spirale, dall'equatore verso nord e poi di nuovo giù verso l'equatore e ancor più giù, verso sud, per poi risalire di nuovo, con una altalena che ciclicamente si ripete ogni anno.

Così, nell'impero meccanico che abbiamo creato, il tempo “vero”, quello che gli orologi neppure immaginano possa esistere, il tempo che una volta ci donava ore disuguali, e giorni più lunghi e più brevi, infine è stato deposto e sostituito da quello sintetico e “falso”, eufemisticamente chiamato “medio”. E si parla di “correzione” per dire che l'ora del Sole va adeguata a quella delle macchine.

In realtà le cose stanno proprio all'opposto: la correzione è qualcosa che riporta la menzogna a divenire verità. Questo è, l'analemma: un giustiziere che sa quale quota di bugia vi sia in ogni istante, nel tempo dichiarato da un orologio, che mai indovinerà, di suo, a quale ora precisa, il Sole giungerà all'apice del suo quotidiano cammino.

 

Analisi di casi particolari di analemma - Caso n.1

Posizionamento a terra: Coordinate 0° Nord, 0° Est (Equatore, Greenwich) a 500 Km Sud dalla costa della Guinea.

Ipotesi: Orbita della Terra circolare, il Sole si trova sul piano equatoriale.

Conseguenze: non esistono i Tropici, niente frutti tropicali o vacanze alle Seychelles, Arthur Miller avrebbe dovuto trovare altri titoli per i suoi romanzi, niente stagioni e… niente analemma.

(I Tropici  sono i paralleli di latitudine 23°26'16" N e S, corrispondenti all'angolo di inclinazione dell'asse terrestre rispetto alla perpendicolare al piano dell' orbita.  Essi rappresentano la massima latitudine, a nord e a sud dell equatore, alle quali il Sole  può raggiungere il suo Zenit; per entrambi gli emisferi ciò avviene in occasione dei rispettivi  solstizi estivi, intorno al 21 giugno per l'emisfero Nord e al 21 dicembre per l' emisfero sud. Dal punto di vista climatico-geografico i tropici separano la fascia intertropicale da quelle temperate delle medie latitudini. La fascia di terra tra essi compresa è detta appunto fascia torrida o fascia tropicale.

L'appena citato Zenit  è , invece, il punto di intersezione tra la linea perpendicolare al piano  dell'orizzonte passante per l'osservatore, con la superficie dell'emisfero celeste visibile. In sintesi è il punto immaginario che sta esattamente sopra la testa dell'osservatore. Il punto diametralmente opposto allo Zenit invece, è detto Nadir. Zenit e Nadir sono anche chiamati poli dell'orizzonte.)

Il motivo per cui non abbiamo alcun analemma, lo si capisce osservando la figura.

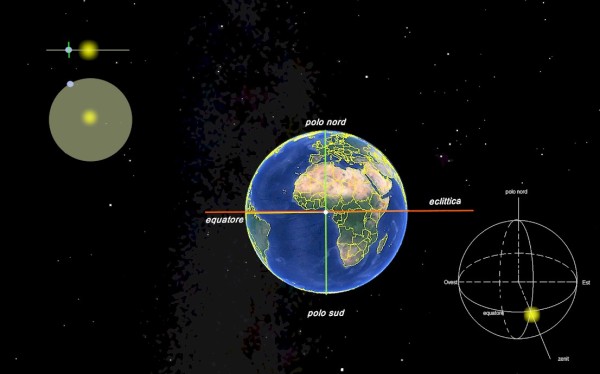
Sulla sfera celeste il sole percorre la circonferenza dell'equatore ed è costantemente perpendicolare all'equatore terrestre. La rotazione della Terra su se stessa la riporta in 24 ore ad allineare il meridiano locale con il Sole, sempre al culmine. Non vi sono ritardi né anticipi nel passaggio al meridiano in nessun giorno dell'anno. Al momento del passaggio il sole si trova sempre allo Zenit.

Quindi l'analemma si riduce ad un preciso unico punto, sulla verticale dell'osservatore.

Nella figura in alto a sinistra sono evidenziate le caratteristiche: l'orbita circolare, l'asse terrestre perpendicolare al piano dell'equatore che è coincidente con il piano dell'eclittica.

Nella figura al centro si nota la posizione dell'osservatore terrestre, all'incrocio tra il meridiano di Greenwich e l'Equatore. Il puntino bianco all'intersezione è il punto analemmatico, l'unico di questo caso particolare.

 

Analisi di casi particolari di analemma - Caso n.2

Posizionamento a terra: Coordinate 0° Nord, 0° Est (Equatore, Greenwich) a 500 Km Sud dalla costa della Guinea.

Ipotesi: Orbita della Terra circolare, il Sole si trova sul piano della eclittica, inclinato di 23,5°

Conseguenze: in questo caso i Tropici esistono e anche le stagioni. Il tracciato dell'analemma è simmetrico perché il raggio di curvatura dell'orbita è costante e tale è pure la velocità di percorrenza nel moto di rivoluzione della Terra.

Il motivo lo si capisce osservando la figura.

 

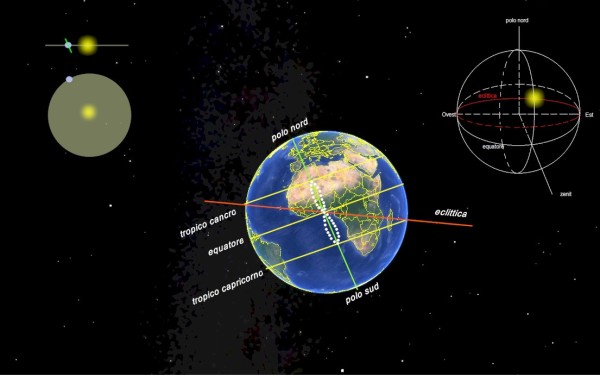
Sulla sfera celeste il sole percorre la circonferenza dell'eclittica e si troverà sopra l'equatore formando un angolo con la verticale verso lo Zenit che varia giorno per giorno, oscillando tra i limiti di 23.5° in più o in meno. La posizione evidenziata in primo piano sulla sfera celeste lo mostra a Nord dell'Equatore, ma sei mesi dopo si troverà sull'altro lato, verso Sud. Questo fatto comporta la diversa posizione del Sole sull'analemma per ciò che riguarda l'elevazione sopra l'orizzonte. Esiste contemporaneamente un effetto di ritardo e anticipo di culminazione dovuto al fatto che la misura del tempo avviene non sull'eclittica, ma sulla sua proiezione sul piano equatoriale. Quindi la percorrenza a velocità costante del Sole sull’eclittica si traduce in una percorrenza a velocità variabile sulla sua proiezione, che non ha più forma circolare ma ellittica. La modulazione della velocità che viene così a prodursi è quella di una sinusoide con periodo semestrale, che non presenta ritardi o anticipi unicamente in corrispondenza di equinozi e solstizi. Al momento del passaggio al meridiano, in un generico giorno, il Sole si trova ad una elevazione specifica, con scostamenti nell'allineamento al meridiano che raggiungono valori di quasi 10 minuti.

Nella figura in alto a sinistra sono evidenziate le caratteristiche: l'orbita circolare, l'asse terrestre perpendicolare al piano dell'equatore, che è inclinato di 23,5° rispetto al piano dell'eclittica.

Nella figura al centro si nota la posizione dell'osservatore terrestre, all'incrocio tra il meridiano di Greenwich e l'Equatore. La figura dell'analemma è simmetrica, a forma di otto, centrata sul punto in cui si trova l'osservatore e si estende da un tropico all'altro in direzione Nord-Sud.

 

Analisi di casi particolari di analemma - Caso n.3

Posizionamento a terra: Coordinate 0° Nord, 0° Est (Equatore, Greenwich) a 500 Km Sud dalla costa della Guinea.

Ipotesi: Orbita della Terra ellittica, il Sole si trova sul piano equatoriale.

Conseguenze: non esistono i Tropici né tutto il resto già elencato ma l'analemma, sia pure molto semplice, non è un punto isolato come visto nel caso n.1

Il motivo lo si capisce osservando la figura.

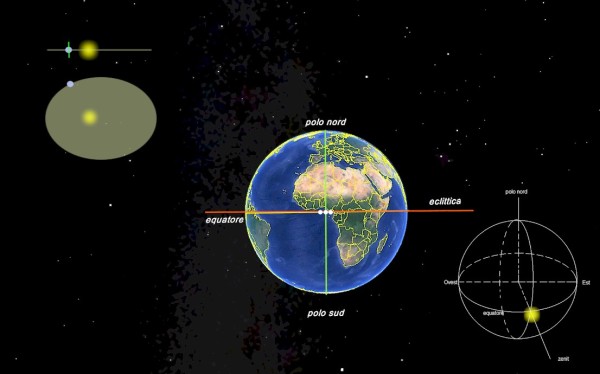
Sulla sfera celeste il sole percorre la circonferenza dell'equatore ed è costantemente perpendicolare all'equatore terrestre. La rotazione della Terra su se stessa la riporta in 24 ore ad allineare il meridiano locale con il Sole, sempre al culmine. A causa della forma ellittica dell'orbita terrestre in alcuni momenti la velocità è superiore alla media ed in altri momenti è inferiore. Questo fatto, ben spiegato dalla seconda legge di Keplero, determina ritardi ed anticipi nell'allineamento al meridiano che si susseguono secondo una legge sinusoidale con periodo annuale. Al momento del passaggio al meridiano il sole si trova sempre allo Zenit ma in generale in una posizione attardata o anticipata, quindi l'analemma è costituito da un segmento allineato alla direzione Est-Ovest, sulla verticale dell'osservatore.

Nella figura in alto a sinistra sono evidenziate le caratteristiche: l'orbita ellittica, l'asse terrestre perpendicolare al piano dell'equatore che è coincidente con il piano dell'eclittica.

Nella figura al centro si nota la posizione dell'osservatore terrestre, all'incrocio tra il meridiano di Greenwich e l'Equatore. Il puntini bianchi allineati sull'equatore, in corrispondenza all'intersezione, rappresentano l'analemma per questo caso particolare.

 

Analisi di casi particolari di analemma - Caso n.4

Posizionamento a terra: Coordinate 0° Nord, 0° Est (Equatore, Greenwich) a 500 Km Sud dalla costa della Guinea.

Ipotesi: Orbita della Terra ellittica, il Sole si trova sul piano della eclittica, inclinato di 23,5°

Conseguenze: in questo caso i Tropici esistono e anche le stagioni. Il tracciato dell'analemma non è simmetrico perché il raggio di curvatura dell'orbita è variabile e tale è pure la velocità di percorrenza dell'orbita nel moto di rivoluzione della Terra.

Il motivo lo si capisce osservando la figura.

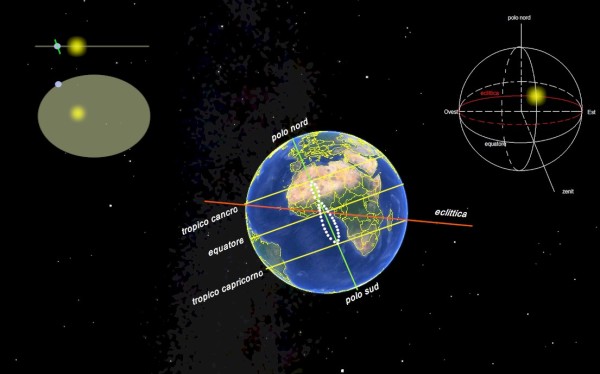
Questo caso è quello che, pur con semplificazioni e approssimazioni, per fenomeni secondari che vengono trascurati, si avvicina più degli altri alla situazione reale.

Sulla sfera celeste il sole percorre la circonferenza dell'eclittica e si troverà sopra l'equatore formando un angolo con la verticale verso lo Zenit che varia giorno per giorno, oscillando tra i limiti di 23.5° in più o in meno. La posizione evidenziata in primo piano sulla sfera celeste lo mostra a Nord dell'Equatore, ma sei mesi dopo si troverà sull'altro lato, verso Sud. Questo fatto comporta la diversa posizione del Sole sull'analemma per ciò che riguarda l'elevazione sopra l'orizzonte. Esiste contemporaneamente un effetto di ritardo e anticipo di culminazione dovuto al fatto che la misura del tempo avviene non sull'eclittica, ma sulla sua proiezione sul piano equatoriale. Quindi la percorrenza a velocità costante del Sole sull’eclittica , si traduce in una percorrenza a velocità variabile sulla sua proiezione, che non ha più forma circolare ma ellittica. La modulazione della velocità che viene così a prodursi è quella di una sinusoide con periodo semestrale, che non presenta ritardi o anticipi unicamente in corrispondenza di equinozi e solstizi.

Ma a questo effetto va a sommarsi quello prodotto dalla intrinseca eccentricità dell'orbita di rivoluzione, già visto studiando il caso n.3, quindi la simmetria dei due “lobi” dell'analemma verrà alterata per l'apporto di questi ulteriori scostamenti.

Al momento del passaggio al meridiano, in un generico giorno, il Sole si trova ad un’ elevazione specifica, con un ritardo/anticipo nell'allineamento che può raggiungere, per l'effetto congiunto delle due cause, valori estremi da 14 a 16 minuti. Neanche i passaggi al meridiano senza ritardi o anticipi avverranno più nei giorni degli equinozi, come nel caso di orbita circolare, ma con sfasamenti di circa due settimane in ritardo, in primavera e tre settimane in anticipo, in autunno.

Nella figura in alto a sinistra sono evidenziate le caratteristiche: l'orbita ellittica, l'asse terrestre perpendicolare al piano dell'equatore, che è inclinato di 23,5° rispetto al piano dell'eclittica.

Nella figura al centro si nota la posizione dell'osservatore terrestre, all'incrocio tra il meridiano di Greenwich e l'Equatore. La figura dell'analemma è asimmetrica a forma di otto, con il lobo più ampio verso Sud, centrata sul punto in cui si trova l'osservatore e si estende da un tropico all'altro in direzione Nord-Sud.

Prima di passare all'esame dei casi che seguono vorrei invitarvi a fare una considerazione generale. La sfera celeste che nelle figure viste fin qui ci è apparsa dall'esterno, immersa nel buio dello spazio, la vediamo in realtà in ogni momento della nostra vita, dall'interno, con il colore, appunto celeste, del cielo, grazie agli infiniti microscopici specchi che diffondono la luce e altro non sono che le molecole dei gas che compongono la nostra atmosfera.

Se abbiamo visto, dall'alto, il punto dell'equatore su cui si sviluppava la sinuosa curva analemmatica, ora vedremo da “dentro”, che questa curva non fa altro che abbassarsi sul nostro orizzonte quanto più risaliamo dall'equatore verso il polo Nord. Per ogni grado della nostra risalita, l'analemma scenderà di altrettanto, fino ad immergersi ad un certo punto dietro la curvatura dell'orizzonte terrestre. Continueremo a vederlo integralmente finché, la nostra latitudine non sarà divenuta così elevata che l'orizzonte eroderà un pezzetto di analemma, quello ormai troppo basso per essere visibile dal circolo polare artico.

Poi, verso il Polo, supponendo che il periodo ci porti dalla stagione primaverile a quella autunnale, continueremo a vederne una parte che si ridurrà sempre più, fino a dimezzarsi.

Ripercorriamo ora i quattro casi già visti, modificando solo la nostra postazione a Terra. Ciò che si può dire, se il nostro movimento verso Nord si sviluppa lungo il meridiano di riferimento di Greenwich, lo si può dire per qualsiasi altro meridiano. Ciò che conta è, semplicemente, la latitudine.

Allora immaginiamo di trovarci a Cuneo.... vedrete che si è gia radunata una piccola folla.

 

Rassegna dei casi già studiati, con il nuovo Posizionamento: latitudine di Cuneo 45° Nord

Nel CASO 1, ricorderete, le ipotesi erano: Orbita della Terra circolare, il Sole si trova sul piano equatoriale.

Conseguenze: non esistono i Tropici, niente frutti tropicali o vacanze alle Seychelles, Arthur Miller avrebbe dovuto trovare altri titoli per i suoi romanzi, niente stagioni e … niente analemma.

Nulla cambia sulla sfera celeste tracciata nella figura. Siamo noi che ci siamo spostati.

I raggi del sole che all'equatore giungono perpendicolari (90° - 0° )= 90°, alla nostra latitudine avranno l'inclinazione di (90°- 45°) = 45°, certo, siamo proprio a metà strada tra l'Equatore e il Polo Nord.

Quindi il Sole lo vedremo 45° sopra l'orizzonte, e per via delle ipotesi ora formulate, sul nostro meridiano e con quella elevazione, il Sole passerà ogni giorno alla stessa ora, senza mai tardare o anticipare. Se volessimo fotografarlo per avere una traccia dell'analemma, mentre all'equatore avremmo dovuto puntare l'obiettivo allo Zenit, ora lo dobbiamo puntare verso Sud con una inclinazione di 45° e centreremo proprio quel bersaglio.

Dall'interno della sfera celeste quello che potremo vedere, disegnando con un visore le linee delle coordinate nel cielo sarebbe quanto è rappresentato nella figura che segue.

Nel CASO 2...

Ipotesi: Orbita della Terra circolare, il Sole si trova sul piano della eclittica, inclinato di 23,5°

Conseguenze: in questo caso i Tropici esistono e anche le stagioni. Il tracciato dell'analemma è simmetrico perché il raggio di curvatura dell'orbita è costante e tale è pure la velocità di percorrenza nel moto di rivoluzione della Terra.

Dalla Piazza vedremo l'analemma simmetrico ed il suo centro sarà ad una elevazione di 45°.

Siamo giunti al CASO 3.

Ipotesi: Orbita della Terra ellittica, il Sole si trova sul piano equatoriale.

Conseguenze: non esistono i Tropici né tutto il resto già elencato ma l'analemma, sia pure molto semplice, non è un punto isolato come visto nel caso n.1

Ecco come vedremo dalla Piazza il segmento che ora è allineato all'altezza di 45° sull'orizzonte.

Ricordiamo infine le ipotesi alla base dell'ultimo CASO 4, quello “reale”.

Ipotesi: Orbita della Terra ellittica, il Sole si trova sul piano della eclittica, inclinato di 23,5°

Conseguenze: in questo caso i Tropici esistono e anche le stagioni. Il tracciato dell'analemma non è simmetrico perché il raggio di curvatura dell'orbita è variabile e tale è pure la velocità di percorrenza dell'orbita nel moto di rivoluzione della Terra.

Anche ora dobbiamo avere ben in mente che la disposizione del Sole, la velocità di rotazione sull'orbita, tutto quanto concorre a definire l'analemma, è qualcosa che non dipende dal nostro girovagare sulla superficie terrestre. Quello che riusciamo a cambiare con il nostro spostamento è solo la nostra visibilità di qualcosa che è tale e quale ovunque. Questo è particolarmente vero quando parliamo dell'analemma osservato al momento della culminazione, ma anche se scattassimo le fotografie, anziché verso Sud, verso Est, troveremmo sempre la medesima figura. Unica differenza l'obliquità del suo asse, che sarebbe inclinato come la latitudine del luogo.

Ovviamente, quando osserviamo verso Sud, abbiamo una vista frontale della figura quindi, in ogni caso, ci appare sempre in posizione verticale.

Nella figura seguente possiamo osservare come, puntando la nostra macchina fotografica con inclinazione di 45°, verso il meridiano locale e scattando pose opportunamente intervallate nel corso dell'anno, ci apparirebbe la ormai familiare figura a forma di 8 asimmetrico.

 

Non ci resta che l'ultima tappa del nostro viaggio verso Nord: il Polo Nord

Posizioniamoci quindi, ben protetti da adeguati abiti e con una scorta di caffè bollente, al Polo Nord e osserviamo cosa rimarrà da vedere dell'analemma a quella latitudine estrema. Naturalmente, in due casi, ciò che vedremo si riferisce solo ai sei mesi, da marzo a settembre in cui il polo del nostro emisfero è illuminato. Sarebbe davvero curioso riuscire a fotografare il Sole “di notte”.

 

Caso n.1

Ipotesi: Orbita della Terra circolare, il Sole si trova sul piano equatoriale.

Conseguenze: non esistono i Tropici, niente frutti tropicali o vacanze alle Seychelles, Arthur Miller avrebbe dovuto trovare altri titoli per i suoi romanzi, niente stagioni e… niente analemma.

I raggi del sole giungono radenti al suolo. In questo primo caso nessuno dei due poli resta al buio: tutto l'anno il Sole circolerà lungo l'orizzonte scaldando comunque ben poco, proprio per via della sua incapacità di colpire, in quella posizione, il terreno con i suoi raggi.

 

La situazione cambia nel caso n.2

Ipotesi: Orbita della Terra circolare, il Sole si trova sul piano della eclittica, inclinato di 23,5°

Conseguenze: in questo caso i Tropici esistono e anche le stagioni. Il tracciato dell'analemma è simmetrico perché il raggio di curvatura dell'orbita è costante e tale è pure la velocità di percorrenza nel moto di rivoluzione della Terra.

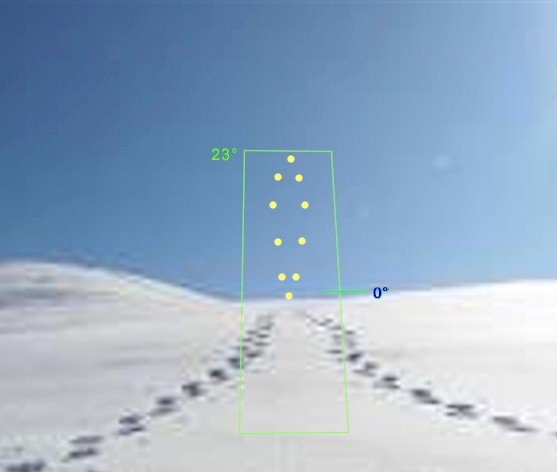
Nel corso dei sei mesi di luce è possibile scattare le foto, con la macchina che punta all'orizzonte, cogliendo le varie posizioni che ci fanno riconoscere la “mezza elica simmetrica” tipica di questo caso che ormai conosciamo.

Il punto di maggiore elevazione del Sole raggiunge i 23,5° (attenzione, non stiamo parlando di temperature...) e ciò avviene in corrispondenza del solstizio estivo, quando l'irraggiamento è massimo.

 

Passiamo quindi al caso n.3

Ipotesi: Orbita della Terra ellittica, il Sole si trova sul piano equatoriale.

Conseguenze: non esistono i Tropici né tutto il resto già elencato ma l'analemma, sia pure molto semplice, non è un punto isolato come visto nel caso n.1

Questa configurazione ci riporta in un mondo senza stagioni, con i poli costantemente illuminati con una luce orizzontale e ombre infinite. Quello che possiamo aspettarci di vedere, a causa dei ritardi e anticipi introdotti dalla ellitticità dell'orbita terrestre, è solo un segmento orizzontale laddove, nella ipotesi 1, vedevamo un punto, niente di più.

 

Infine il caso 4, sempre al Polo Nord...

Ipotesi: Orbita della Terra ellittica, il Sole si trova sul piano della eclittica, inclinato di 23,5°

Conseguenze: in questo caso i Tropici esistono e anche le stagioni. Il tracciato dell'analemma non è simmetrico perché il raggio di curvatura dell'orbita è variabile e tale è pure la velocità di percorrenza nel moto di rivoluzione della Terra.

Ciò che vediamo è comunque metà dell'analemma. Non lasciamoci ingannare dal fatto che il lobo superiore, essendo più piccolo dà la sensazione di vederne una parte maggiore. Per i sei mesi da settembre a marzo, in questo luogo inaccessibile, regnerà il buio della lunga notte artica.

Non resta a questo punto che ringraziare tutti coloro che sono arrivati a leggere fin qui, (non metto mai i ringraziamenti a metà della storia) nella speranza che riescano a diffondere a loro volta queste conoscenze.

Provate con parenti e amici, cominciando con quelli a cui tenete meno...