Questo quiz puramente geometrico appare, a prima vista, piuttosto difficile. Esistono sicuramente vari metodi per giungere alla soluzione. Tuttavia, ve n’è uno estremamente elegante e decisamente alla portata di tutti. Un bell’esercizio da proporre alle scuole superiori…

Disegniamo un triangolo equilatero ABC e prendiamo un punto qualsiasi O al suo interno. Congiungiamo questo punto con i tre vertici del triangolo. Otteniamo i tre segmenti rosso, azzurro e verde AO, BO e CO. Immaginiamo di conoscere gli angoli AOB e AOC e li chiamiamo α e β.

Non ci resta adesso che costruire un nuovo triangolo, i cui lati siano proprio AO, BO e CO (che sicuramente esiste dato che qualsiasi suo lato DEVE essere minore della somma degli altri due).  Si può agire in vari modi.

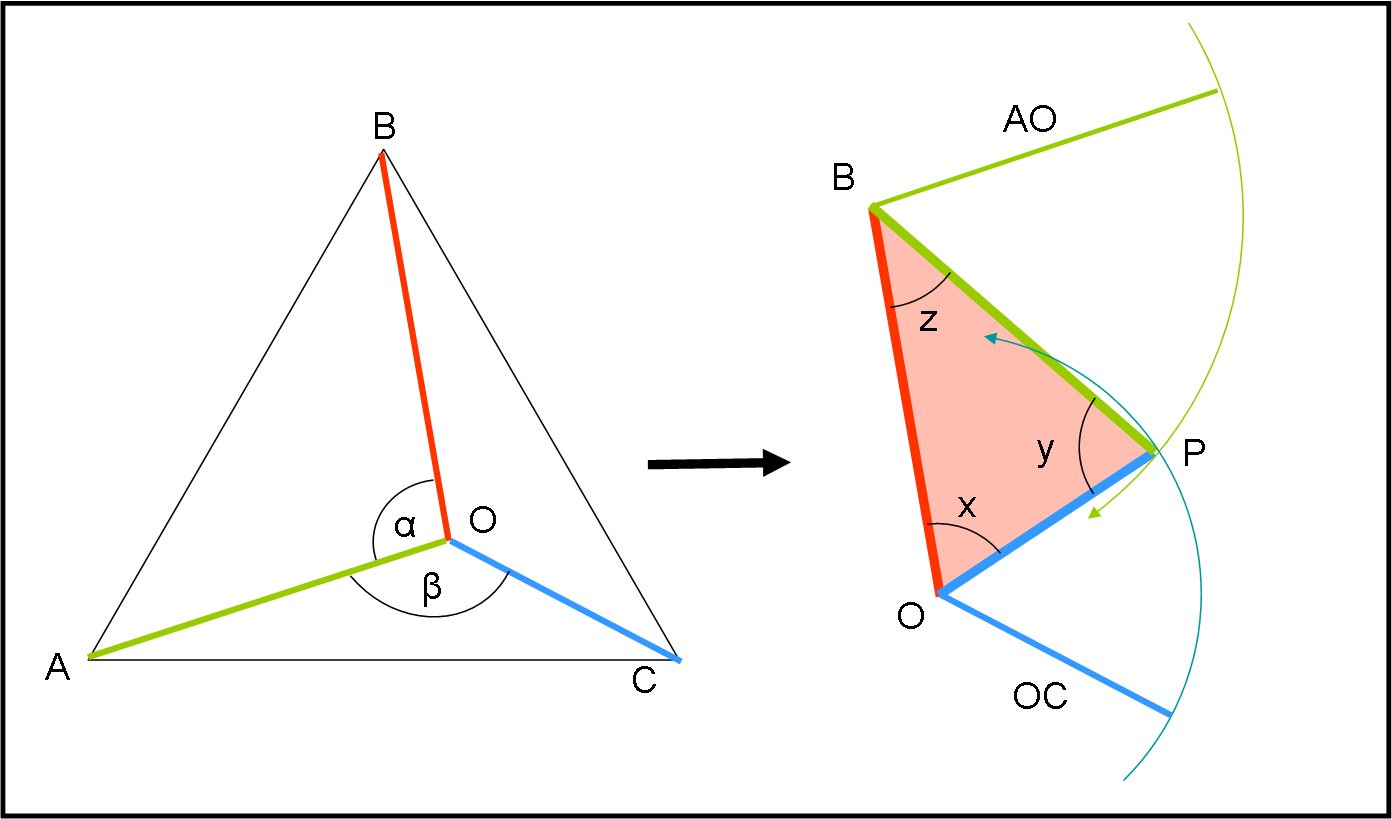
Nella Fig. 1 abbiamo spostato il lato rosso e inserito il lato verde e quello azzurro ai suoi due vertici O e B. Facendo centro in questi vertici basta descrivere due cerchi di raggio uguale ai due segmenti verde (AO) e azzurro (OC) e trovare il loro punto di intersezione P. Tracciando i segmenti che uniscono questo punto con i due vertici si ottiene il triangolo rosa cercato, di lati OB, BP = AO, PO = OC.

Notiamo che esiste un solo triangolo “costruibile”, dato che avere i tre lati uguali implica l’uguaglianza (terzo criterio). Io sono all’antica e uguaglianza e congruenza li vedo praticamente come la stessa cosa.

Si vogliono determinare gli angoli x, y e z del triangolo OBP.

Soluzione QUI