Questo articolo è stato inserito nella pagina d'archivio dedicata all'Astronomia Classica

 

Una semplice meridiana

Cominciamo, per una volta, dalla fine....

Ecco cosa otterrete, con una spesa modestissima, in un tempo ragionevolmente breve, riuscendo (forse ) a coinvolgere i vostri ragazzi: una vera meridiana, funzionante nelle giornate soleggiate, calcolata esattamente per il luogo in cui vivete. Elegante, ecologica, economica e precisissima.

 

Vi occorrerà, oltre alla pazienza di eseguire le varie operazioni, anche un piccolo corredo di materiali e utensili, quasi tutti di uso comune e già in vostro possesso. Questi:

 

L'unica cosa che non avete in casa è il rocchetto di filo di rame, ma potete farne del tutto a meno o utilizzare un filo di rame recuperato da un pezzo di cavo elettrico, che va benissimo. In quanto agli occhiali, a me sono serviti, ma forse voi non ne avrete bisogno.

Quello che dovrete probabilmente acquistare è una lastra di metallo (3 o 4 Euro), per la base della meridiana. Da un solo foglio di lamiera potrete ricavare ben quattro meridiane, posizionate ai quattro angoli, facendo contenti anche amici e parenti. Nei centri di materiale per bricolage si trovano facilmente lastre in lamierino di alluminio di piccole dimensioni (40*50 cm) da cui si possono ricavare facilmente 4 supporti di 24*16 cm, avanzando materiale in abbondanza per realizzare i triangoli gnomonici.

La foto di una lastra da cui è stato ricavato un rettangolo di supporto.

Una raccomandazione da non sottovalutare è di sbordare con una lima dolce a taglio fine, subito dopo il taglio con le cesoie, tutto il perimetro della lamiera per rimuovere le sbavature che inevitabilmente si saranno formate a causa delle caratteristiche meccaniche dell'alluminio.

Per realizzare il disegno delle linee orarie e del triangolo chiamato "gnomone" che, proiettando su di esse la sua ombra, fungerà da "lancetta" dell'orologio solare, possiamo  avvalerci  di un supporto di calcolo e di tracciatura dei grafici che consente di realizzare facilmente il quadrante solare con tutti gli elementi necessari.

Il programma, scaricabile gratuitamente è shadows 4.1 , di facile installazione e uso.

Nella Figura  vediamo la pagina iniziale.

Scegliendo l'opzione in alto a sinistra realizzeremo la meridiana orizzontale.

I dati da fornire successivamente saranno semplicemente la città o le sue coordinate, l'opzione per la numerazione delle ore con le consuete cifre o quelle romane, la rappresentazione dell'analemma e il suo posizionamento in funzione dello scarto di longitudine del luogo, l'eventuale motto da scegliere in un elenco o da personalizzare a piacere.

L'esplorazione del programma è veloce e intuitiva e da esso otterremo le due cose essenziali per la nostra costruzione: il quadrante con le rette orarie e il triangolo gnomonico. Vediamole in faccia...

Questo è il quadrante, calcolato per la città di Milano. Se preferite le cifre romane per indicare le ore non avete che da dirlo durante l'esecuzione del programma. La suddivisione scelta è di mezz'ora in mezz'ora e  il buffo scarabocchio a forma di otto, richiesto in fase di scelta dei parametri, cliccando sull'icona corrispondente, non è altro che la correzione oraria stagionale, il famoso "analemma".

Questo , invece è lo "Gnomone" di cui parlavamo. Va fissato con grande cura e precisione sulla linea AB tratteggiata sopra al quadrante.

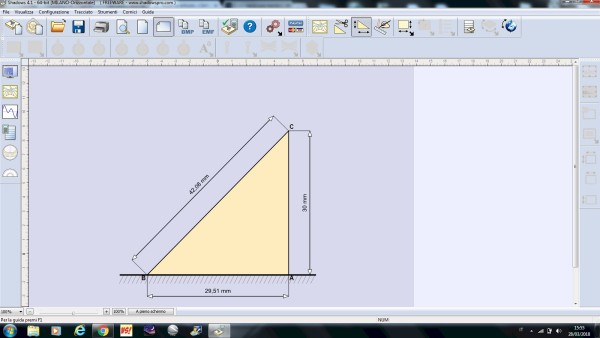
Una volta prodotta la figura del quadrante solare e del triangolo gnomonico in scala, resta il problema di trasferire questi elementi su un supporto che non sia un semplice foglio di carta.

Se la base rettangolare di lamierino di alluminio l'abbiamo già predisposta, senza problemi, dobbiamo solo avere qualche accortezza in più per lo gnomone. Se ritagliassimo il triangolo come ce lo propone la figura, non disporremmo di una base di contatto con cui fissarlo, in verticale, sopra il quadrante. Occorre quindi un piccolo accorgimento, illustrato in questo disegno.

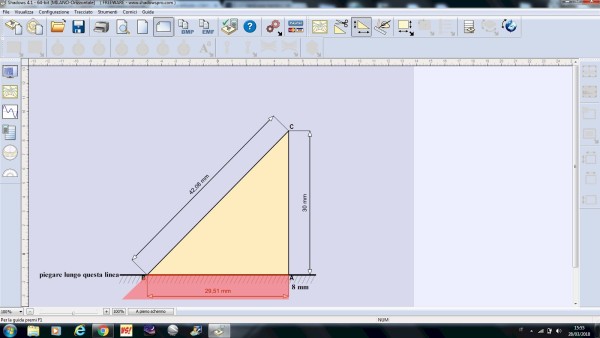
Si tratta solo di prolungare di 8 mm la figura del triangolo verso il basso , ritagliare questo triangolo maggiorato nella lamiera rimasta dopo avere ricavato i rettangoli delle basi, e piegare con cura, a 90° , lungo la linea orizzontale, in modo da realizzare la base di contatto.

La plasticità del metallo consentirà una facile piegatura del piede di sostegno, come vediamo nella foto.

Non resta che mettere insieme il tutto...

Questo disegno, che raffigura il quadrante, va poggiato sulla base rettangolare che abbiamo ritagliato prima,  senza per ora incollarlo.

Con il punteruolo segniamo i punti A e B lasciando una traccia sul sottostante metallo.

Rimuoviamo il disegno e applichiamo un sottile velo di colla Attak sotto il piede del triangolo gnomonico, posizionando la sua base in modo preciso tra i due punti segnati, facendo attenzione che l'altezza del triangolo si elevi sopra il punto A. Esercitando un forte pressione sulla parte da incollare, si otterrà rapidamente una presa soddisfacente. Ecco il risultato:

Ora, con il taglierino, pratichiamo una incisione sulla carta lungo il segmento AB e, posizionando il foglio sopra la punta del triangolo appena fissato, facciamolo scendere con precisione fino al piano di supporto in modo che i punti A e B vadano a corrispondere agli estremi della base del triangolo. Passiamo infine un filo di colla attorno al perimetro del foglio e fissiamolo al perimetro del supporto senza lasciare ondulazioni o grinze.

Volendo possiamo applicare il sottile filo di rame, ricavato da un cavo elettrico, per la lunghezza necessaria, circa 25 cm, lungo l'iperbole del giorno che ci interessa evidenziare. L'iperbole si può disegnare semplicemente  interpolandola da quelle contigue. Utilizzando una punta sottile applicheremo una piccola goccia di colla istantanea nei punti di intersezione dell'iperbole con le rette orarie e faremo aderire il filo al foglio in questi punti.

Ecco fatto! Il lavoro è concluso e non resta che collaudare il risultato.

La meridiana va posta in modo che l'ipotenusa dello gnomone punti alla stella Polare. La cosa si ottiene automaticamente allineando la linea meridiana (quella delle ore 12) alla direzione nord sud. Come farlo senza bussola? Semplice: la posizione del Sole a mezzogiorno indica il sud, ma attenzione... se è in vigore l'ora legale è alle 11 che il Sole indica il sud.

L'altezza del triangolo sarà rivolta a Nord, come nella foto. E' anche fondamentale che il piano della base sia perfettamente orizzontale,  una cosa che si può facilmente verificare con una semplice livella a bolla d'aria.

Se non siamo certi della direzione del nord (e non vogliamo attendere che sia mezzogiorno per individuare il sud), la cosa migliore da fare è  semplicemente ruotare la meridiana in modo che l'ombra segni l'ora dell'orologio. Poi valutiamo quale correzione vada applicata (utilizzando l'analemma) e ruotiamo ancora la meridiana in modo che, applicando l'entità della correzione, risulti l'ora dell'orologio. In questo modo la direzione del triangolo indica il Nord. In pratica abbiamo creato una bussola, percorrendo in senso inverso le operazioni di posizionamento.

Da quel momento possiamo monitorare il progredire delle indicazioni e valutare la precisione della nostra realizzazione. Un test preciso lo potete organizzare il 15 di aprile. In quel giorno la correzione stagionale vale zero, e potete verificare facilmente se avete posizionato correttamente la direzione della meridiana. Quando il vostro orologio segnerà le ore 13 + i minuti che tengono conto dello scostamento della vostra località dal meridiano del fuso orario (per Milano sono 23 o 24 minuti , dall'estremo est all'estremo ovest della città), l'ombra dello gnomone dovrà indicare le ore 12 precise. Se così non fosse la ruoterete di quel tanto che basta affinché segni le 12, e in quella posizione dovrà stare sempre. Quindi, se la dovrete rimuovere, segnatevi dei riferimenti per riposizionarla successivamente

Il programma che vi ha fornito il disegno del quadrante e dello gnomone consente di avere anche il grafico della "equazione oraria" cioè la curva che vi indica , giorno per giorno, quanti minuti dovete sommare per via della posizione geografica della vostra città e per la variabilità stagionale. Potete stampare anche questo diagramma che vi sarà utile per controllare la precisione delle letture.

E non dimenticate che da fine marzo a fine ottobre è in vigore l'ora legale...

Non è detto che si debba costruire una meridiana solo per il luogo in cui ci troviamo.

Possiamo benissimo costruirne una, stando in città, per un luogo al mare o in montagna dove pensiamo di trascorrere le vacanze. Oppure, per regalarla ad un amico che abita in un'altra città, addirittura in un'altra nazione. Il procedimento è il medesimo e il programma può realizzare disegni per qualsiasi luogo anche sperduto, fornendone le coordinate.

Ma se dobbiamo trasportare il nostro regalo in un luogo lontano non converrebbe trovare un modo per proteggere un oggetto così delicato e preciso?

Certamente!

Ecco un suggerimento per realizzare un contenitore che protegga la nostra opera durante il trasporto o, semplicemente, ci consenta di allinearla su uno scaffale tra i nostri libri preferiti, in attesa di utilizzarla in una bella giornata di sole.

Da uno scatolone di cartone ritagliamo il modello illustrato, con le misure riportate.

Piegando i margini laterali e poi seguendo il tracciato degli intagli realizzeremo in brevissimo tempo una scatola delle giuste proporzioni in cui infilare senza problemi la meridiana. Utile accorgimento per evitare schiacciamenti è inserire uno spessore di polistirolo, (come quello che vedete nella precedente foto della lastra di alluminio)  in prossimità del lembo di apertura, facendolo penetrare verso l'interno. Questo proteggerà il triangolo gnomonico da possibili pressioni e deformazioni.

Sulla costa della scatola possiamo mettere un'etichetta che individui la città per cui è stata realizzata la meridiana ed eventualmente l'indicazione di quanti minuti in più o in meno corrispondono allo scarto di latitudine di quella località.

Nella figura 12 alcuna meridiane in attesa di essere distribuite agli amici di Firenze, La Spezia, Asti...

 

Per chi volesse un risultato più solido e definitivo, suggeriamo di utilizzare il disegno applicato alla basetta come modello per trasferire le linee orarie, le iperboli, l'analemma, le numerazioni e le diciture, direttamente sulla lastra di alluminio. Basterà segnare i punti di riferimento e copiare le tracce incidendo delicatamente con una punta la superficie, dopo aver rimosso la carta.

Con un pennarello permanente a punta sottile sarà poi facile riempire i solchi, eventualmente con colori diversi per ottenere l'effetto desiderato e non rischiare che, avendo dimenticato sul tavolo in giardino la meridiana, un temporale notturno la possa danneggiare, disintegrando il disegno su carta.

Non vi resta che provare... Se avete dubbi , le istruzioni vi appaiono poco chiare, vi occorre qualche spiegazione in più, non esitate a inserire le vostre osservazioni in un commento. Potrà essere utile anche ad altri lettori. Se poi avete voglia di inserire nel commento la foto della "vostra" meridiana, saremo lieti di ammirarla.

 

Appendice per i più curiosi.

La costruzione di una meridiana, avendo le necessarie istruzioni, si risolve, come abbiamo visto, nella esecuzione di una semplice sequenza di operazioni manuali. Ma è certo più interessante capire cosa c'è dietro quella costruzione grafica e come nascono quelle curve che vengono disciplinatamente percorse dall'ombra dello stilo nel corso delle varie ore del giorno e delle stagioni.

Con un piccolo numero di figure, senza calcoli matematici, ma solo con elementari ed intuitive considerazioni geometriche sarà possibile tracciare correttamente tutte le linee che ci interessano.

 

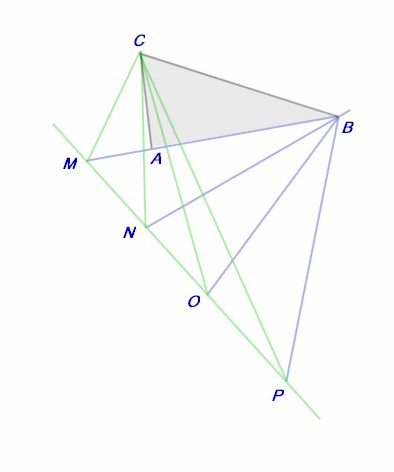
In questa Figura 1 ho rappresentato il triangolo rettangolo ABC. Pensiamolo costituito da una lastra solida fissata in verticale con il lato AB posato di costa sul piano orizzontale. L'angolo in A è retto e il segmento AC è lo stilo che proietta l'ombra del sole sul piano orizzontale.

Il punto B è allineato con A in modo che la direzione AB punti a Sud.

L'angolo ABC è dato dalla latitudine del luogo in cui ci troviamo. In questo modo l'ipotenusa del triangolo, da B verso C, punta alla stella Polare, direzione Nord e elevazione pari alla latitudine,

Questo triangolo “gnomonico” è il nostro punto di partenza.

Immaginiamo di osservare l'ombra del sole nel giorno dell'equinozio di primavera (20 marzo) nel momento in cui transita al meridiano locale, cioè a Sud.

In questo giorno particolare i raggi del sole giungono perpendicolari all'asse di rotazione della Terra. L'ipotenusa BC è parallela a questo asse. Pertanto il vertice C del triangolo proietterà la sua ombra nel punto M. La retta che passa da B e da M si chiama “linea meridiana” ed è proprio la direzione in cui, al mezzogiorno locale, viene proiettata, di taglio, l'ombra del triangolo.

La direzione dell'ombra lungo la congiungente CM è quindi perpendicolare all'ipotenusa.

Il piano che contiene CM ed è perpendicolare a CB è il piano che nel giorno dell'equinozio contiene tutti i raggi del sole in un qualsiasi momento della giornata. La traiettoria che il sole descrive su questo piano non è altro che l'arco dell'equatore celeste.

Pertanto, volendo disegnare l'ombra del triangolo gnomonico ad un ora precedente il mezzogiorno, basta individuare la direzione dei raggi solari a quell'ora. Dato che in 24 ore viene coperto un angolo di 360°, al trascorrere di un'ora l'angolo varierà di 15°. la proiezione dell'ombra del punto C, un'ora prima del mezzogiorno, andrà ad intersecare il piano orizzontale nel punto N. Analogamente, andando all'indietro di ora in ora, avremo i punti O, P etc, mentre, avanzando di ora in ora avremo specularmente altri punti dal lato opposto nel corso del pomeriggio.

L'ombra della ipotenusa BC si formerà sul piano orizzontale lungo le linee BM (a mezzogiorno), BN, BO, BP rispettivamente, nelle ore antecedenti

Tutti i punti M,N,O,P sono allineati sulla linea degli equinozi, che altro non è che l'intersezione del piano orizzontale con il piano equatoriale.

Le rette ottenute collegando il punto B con i punti della linea equinoziale sono le “Rette Orarie”.

Qualunque sia il giorno dell'anno ad una determinata ora l'ombra della ipotenusa sarà sovrapposta alla corrispondente retta oraria.

Abbiamo quindi ottenuto il primo risultato: individuare la linea equinoziale e le rette orarie. La meridiana ci fornisce così l'ora locale per un qualsiasi giorno.

La direzione dell'ombra dell'ipotenusa ci fornisce l'ora ma ci sono altre cose che l'ombra ci può dire, oltre l'ora. Per esempio: alla medesima ora in giorni diversi la lunghezza dell'ombra è diversa. Ciò dipende dal fatto che la “declinazione” del Sole varia di giorno in giorno. Mentre agli equinozi il sole si trova sul piano equatoriale, nei giorni precedenti e successivi, si troverà su un piano differente ed i suoi raggi risulteranno più inclinati o meno inclinati.

Nei mesi invernali il sole è “più basso” sull'orizzonte, on quelli estivi è “più alto”.

La linea che congiunge il punto C con il Sole tenderà ad essere più verticale in estate, raggiungendo la massima inclinazione al solstizio estivo (21 giugno) e più orizzontale in inverno, con l'inclinazione minima nel giorno del solstizio invernale (21 dicembre).

Gli scostamenti dalla inclinazione agli equinozi sono +23,5° e -23,5° valori che dipendono dalla inclinazione dell'asse terrestre rispetto al piano equatoriale.

Come cambierà allora la traccia delle ombre, ad esempio nel giorno del solstizio estivo, rispetto alla linea equinoziale? Ebbene l'ombra ad una determinata ora del giorno sarà sempre più corta, perché il Sole è più in alto. Ma la linea che viene percorsa dall'ombra del punto C non sarà una retta.

Proviamo a capire perché.

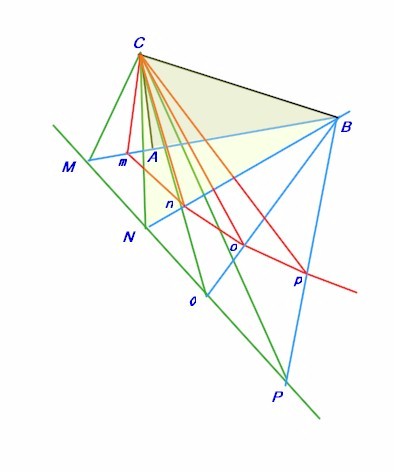
In questa figura 2 ho rappresentato il “seguito” della figura 1. Riconoscerete le linee verdi che

ogni 15°, cioè ogni ora risalendo dal mezzogiorno all'alba, ci hanno permesso di individuare i punti M,N,O,P.

Se consideriamo che al solstizio estivo i raggi del sole provengono da una direzione che è di 23,5° “più verticale” rispetto a quanto era al 21 marzo, e rappresentiamo il percorso dell'ombra con linee rosse, vediamo che a mezzogiorno l'ombra invece di cadere nel punto M sarà arretrata nel punto “m” e sarà più corta di una quantità Mm. Insomma M è retrocesso verso il punto B, centro delle rette orarie. Naturalmente la retta oraria è rimasta la stessa.

La stessa cosa avviene per i punti N che recede in “n”, O, che va in “o”, P che va in “p” eccetera.

Se consideriamo il triangolo CPB, esso individua il piano su cui scivola l'ombra della ipotenusa. Su questo piano la diversa direzione dei raggi del Sole al solstizio forma il triangolo CpB. L'angolo compreso tra CP e Cp è di 23,5°, cioè la “declinazione” del Sole in quel giorno. Naturalmente il ragionamento vale per ciascuna della altre ore in quello stesso giorno.

Per questo motivo la linea che otteniamo congiungendo i punti m,n,o,p non è una retta. Allora di che linea si tratta. Ebbene se pensiamo di rappresentare tutte le “generatrici” come mC, nC, oC, pC,

esse, avendo la medesima inclinazione rispetto al piano equatoriale, costruiranno un cono con il vertice nel punto C.

L'intersezione di tale cono con il piano orizzontale è semplicemente una iperbole, luogo dei punti di tutte le estremità delle ombre del punto C.

Questa iperbole è la linea solstiziale estiva. In modo del tutto simmetrico potremo ottenere la linea solstiziale invernale. Basterà costruirle con i punti ottenuti a fronte di una declinazione di -23,5°.

E' evidente che l'allungamento delle ombre nella stagione invernale darà origine ad una iperbole simile a quella estiva ma situata più distante dalla base del triangolo gnomonico, in direzione opposta.

In ogni giorno il Sole ha una declinazione diversa, che può essere facilmente calcolata. Per comodità possiamo utilizzare la semplice formula di Cooper che definisce, per il giorno N, a partire dal primo giorno dell'anno, il valore dell'angolo di declinazione.

Delta = 23,45° * sen ( 360° * (284+n)/365))

Fissato un giorno si può trovare l'angolo di declinazione corrispondente e tracciare l'iperbole che verrà percorsa in quel giorno dalla estremità dell'ombra.

Avremo così dal quadrante solare non solo l'informazione relativa all'ora, ma anche al giorno dell'anno. In realtà rimane una ambiguità per il fatto che la stessa iperbole vale per due giorno all'anno, tranne nel caso dei solstizi. Pensate semplicemente alla linea equinoziale. Essa è il luogo dei punti dell'ombra al 21 di marzo, ma anche al 22 di settembre, e la stessa cosa vale per ciascuna delle altre linee che possiamo tracciare. Le ombre che vediamo una settimana prima di un solstizio le rivedremo uguali una settimana “dopo”. Quando la declinazione solare, raggiunto il suo valore estremo, ritorna “indietro”.

Occorre ora trasferire questi ragionamenti qualitativi sul piano quantitativo. Un esempio ci consentirà di vedere tutti i passi necessari per costruire graficamente la meridiana.

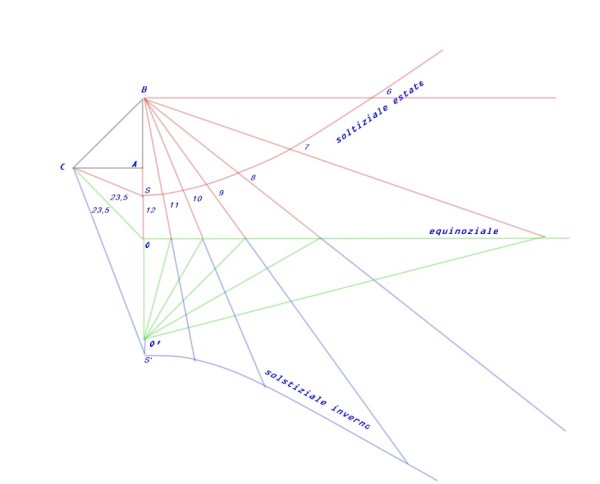
Iniziamo a considerare questa Figura 3, ma presto avremo bisogno anche di un'altra figura per aiutarci a completare la costruzione.

In alto a sinistra appare il triangolo gnomonico ABC. L'angolo in A è retto e quello in B corrisponde al valore della latitudine (nel disegno è quella di Milano: 45,5°).

Disegniamo il segmento CO (verde) che è perpendicolare all'ipotenusa CB ed interseca il prolungamento del segmento BA. La linea verticale che parte da B è la linea meridiana.

La linea orizzontale che parte dal punto O è la linea degli equinozi.

A questo punto riportiamo la distanza OC sulla linea meridiana individuando il punto O'.

Da questo punto disegniamo con intervalli di 15 gradi il “ventaglio” di linee verdi che vanno ad intercettare la linea equinoziale.

Siamo così in grado di tracciare le linee orarie, semplicemente collegando questi punti con il polo B, centro delle rette orarie. Nel disegno è indicata la numerazione dell'ora su ciascuna retta.

Viene ora la parte più difficile, ma non molto. Vediamo quindi la Figura 4.

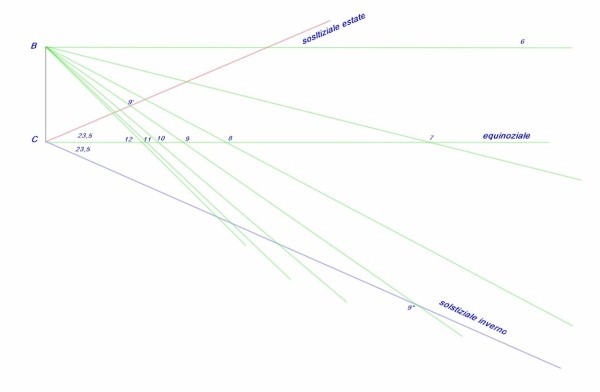
Nella parte alta a sinistra riportiamo in verticale il segmento BC, ipotenusa del triangolo gnomonico.

Partendo da C tracciamo una retta orizzontale che corrisponde alla linea equinoziale. Su questa linea riportiamo ordinatamente (dalla figura 3) le distanze da O' alla linea equinoziale.

Iniziamo con la distanza O'O che riportiamo nella figura 4 da C a ”12”, proseguiamo con la distanza successiva che riportiamo da C a “11” , e così via.

In pratica abbiamo “adagiato” tutti i triangoli su un unico piano vincolandoli sul lato sinistro alla ipotenusa. Sono ovviamente tutti triangoli rettangoli.

A questo punto tracciamo dal punto C una linea che formi un angolo di 23,5° con la linea equinoziale (si tratta dell'angolo di declinazione massimo in estate). Tutti i triangoli verranno “tagliati”da questa retta individuando la misura di cui l'ombra regredisce, a ciascuna ora, nel giorno del solstizio estivo. Ci basterà misurare la distanza, lungo ciascuna retta verde, tra i punti di intersezione con la linea equinoziale e quella solstiziale estiva e riportarla sulla Figura 3 sulla corrispondente retta oraria partendo dalla linea equinoziale risalendo verso il punto B. Collegando tutti i punti così individuati troveremo l'iperbole del solstizio estivo, su cui come si vede sono state riportate le ore locali corrispondenti.

Eseguendo la stessa operazione con un angolo di declinazione di -23,5° potremo costruire l'altra linea solstiziale, per l'inverno, pervenendo infine a tracciare l'iperbole del solstizio invernale.

Questa iperbole è speculare rispetto a quella precedente ed è facile trovare il punto intermedio tra i due vertici. La linea orizzontale che passa per questo punto intermedio ( non rappresentato nella Figura 3) è l'asse di simmetria. Dalla espressione di Cooper si può ricavare il valore di declinazione per un dato giorno e ripetere le operazioni descritte per ottenere nuove iperboli.

Ad esempio, un mese prima dell'equinozio di primavera avremo una declinazione negativa di un certo valore e un mese dopo avremo una declinazione della stessa entità ma di segno positivo. I due rami dell'iperbole saranno speculari e li potremo disegnare con il metodo già visto.

Per una maggiore facilità di lettura si possono tracciare anche le linee orarie intermedie, semplicemente graduando il ventaglio di rette ogni 7,5° invece che ogni 15° come abbiamo visto.

Così potremo contrassegnare le ore e le mezze ore.

A questo punto ci possiamo porre il problema di come correlare l'ora locale, indicata dalla meridiana, all'ora segnata dagli orologi.

Un prima considerazione riguarda la latitudine del luogo rispetto al riferimento dell'ora civile, ossia la latitudine del meridiano centrale del fuso orario.

Se il luogo si trova più ad est del meridiano di riferimento, diciamo al margine estremo,quando la meridiana segna mezzogiorno, l'ora dell'orologio segnerà le 11.30 e solo dopo mezz'ora segnerà mezzogiorno. Viceversa, se il luogo si trova all'estremo margine ovest, l'ombra del mezzogiorno locale apparirà solo quando l'orologio segnerà le 12.30.

Queste differenze sono invariabili nel corso dell'anno, essendo legate unicamente alla differenza di latitudine tra i luoghi e il meridiano di riferimento.

Esiste però anche una fluttuazione stagionale nella indicazione dell'ora locale dovuta alla geometria del sistema solare. I due principali fattori che concorrono nel determinare le variazioni nel momento di culminazione del sole sono la ellitticità dell'orbita terrestre e l'inclinazione dell'asse di rotazione. rispetto al piano dell'eclittica.

Volendo rappresentare sul quadrante della meridiana, in modo sintetico, gli scostamenti che si verificano, quotidianamente, in termini di minuti, basta tracciare una particolare curva detta analemma, posizionata in modo da tener conto anche dello scostamento in longitudine del luogo rispetto al meridiano centrale.

La costruzione dell'analemma parte da una relazione chiamata “equazione del tempo” che esprime, in funzione della posizione della terra sull'orbita, in un determinato giorno, quanti minuti occorre aggiungere o sottrarre all'ora indicata dall'ombra sulla meridiana.

In alternativa possiamo avere una tabella che giorno per giorno da la medesima informazione in termini numerici anziché grafici.

Supponiamo di avere tracciato le rette orarie con intervalli di 30 minuti e la linee delle iperboli per il giorno 21 di ciascun mese. Sarà sufficiente aggiungere una retta oraria posizionata in ritardo o anticipo rispetto al mezzogiorno, di tanti minuti quanti sono quelli dovuti allo scarto di longitudine.

Ad esempio: Milano si trova alla longitudine di circa 9° est mentre il meridiano centrale si trova a 15° est. Aggiungeremo, nella figura 3, a sinistra del primo raggio che individua il punto della retta delle ore 12 (inclinato di 15°) un nuovo raggio inclinato di 9° (longitudine di Milano) per intercettare sulla linea equinoziale il punto della retta oraria corrispondente a 24 minuti prima di mezzogiorno, ossia il momento in cui l'orologio segna le dodici, mentre a Milano mancano proprio 24 minuti alla culminazione.

I punti da riportare attorno a questa retta si troveranno sulle iperboli dei vari mesi con questi valori:

 dicembre -2'

 gennaio +11'                 novembre -14'

febbraio +13'                     ottobre -15'

    marzo +7'                   settembre -7'

    agosto +3'                           aprile -2'

      luglio +6'                        maggio -3'

   giugno +2'

Anche senza costruire ulteriori rette orarie, è possibile posizionare questi punti proporzionando le distanze ai valori, avendo come riferimento le rette già disegnate in prossimità del mezzogiorno.

Basta poi collegare i punti tra loro seguendo lo schema dei mesi nella tabella per avere il tracciato a forma di 8 dell'analemma.

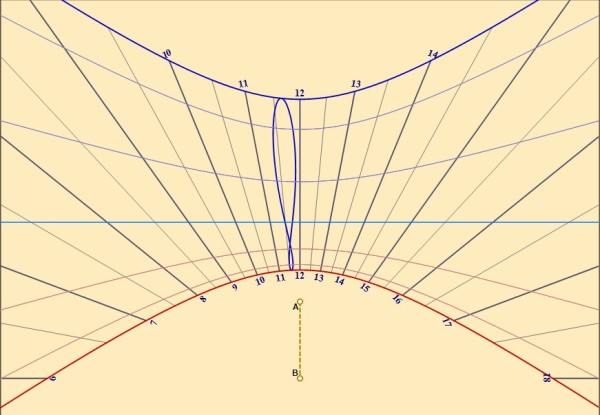
Nella foto qui sotto  vediamo il risultato finale.

Da notare il tratto di linea blu che collega l'indicazione fornita dall'ombra alla linea del mezzogiorno. In questo caso il tratto appare quasi rettilineo, ma in generale sarà curvo, interpolando l'andamento delle iperboli contigue. Il tratto di colore rosso indica i minuti da sommare , in questo giorno alla lettura dell'ora locale.

Il giorno 28 marzo ai 24' dovuti alla longitudine, vanno sommati 5' per l'equazione del tempo.

L'ombra segna le 13.45 ma l'orologio segnerà 29' in più ossia le 14.14. Per la verità, a causa dell'entrata in vigore dell'ora estiva, dovremo aggiungere un'ora in più, quindi saranno le 15.14.

L'iperbole al di sopra della linea equinoziale, delineata da un sottile filo di rame smaltato, è stata aggiunta per indicare un giorno particolare, in questo caso si tratta del giorno 1 ottobre, data di esordio, nel 2013 del blog L'Infinito Teatro del Cosmo. Analogamente si può decidere di segnare in questo modo una data particolare, un compleanno, una ricorrenza, una festa speciale.

 

QUI Oreste Pautasso ci racconta un'avventura estiva che ha per protagonisti una meridiana costruita in giardino grazie ad un nipotino particolarmente sveglio e... un cinghiale!

QUI, invece, il "solito" Oreste applica alle meridiane le fantomatiche matrici di rotazione

QUI, invece, il suo amico Maurizio ci parla di come potrebbe apparire una meridiana realizzata da chi vive sull'equatore.