Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

Prerequisiti:

MATEMATIZZIAMO IL NASTRO DI MÖBIUS ,PARTE 1° : GLI SPAZI METRICI

MATEMATIZZIAMO IL NASTRO DI MÖBIUS ,PARTE 2° : GLI SPAZI TOPOLOGICI,

Dopo aver ridefinito ridefinito la continuità tramite gli aperti ,eccoci arrivati al concetto più importante della topologia:

Gli Omeomorfismi

Una funzione f: X--->Y fra spazi topologici è un omeomorfismo se f è continua, biettiva e la sua inversa  : Y → X è  anch'essa continua.

Due spazi topologici X e Y si dicono omeomorfi e scriviamo  se esiste un omeomorfismo f : X → Y .

Si richiede quindi l'esistenza di una corrispondenza biunivoca f fra X e Y; per quello che abbiamo visto sulle funzioni, se è biunivoca allora la funzione f è invertibile. Si richiede inoltre che anche l'inversa,, sia continua.

Come si può intuire dalla definizione, il concetto di omeomorfismo offre molta libertà;  le trasformazioni indotte sono molto più  sconcertanti di quelle che siamo abituati a vedere, che conservano la "forma" dell'oggetto come l'abbiamo sempre intesa (pensiamo alle traslazioni, rotazioni, simmetrie; un quadrato resta un quadrato e un cerchio anche).

Gli esempi che faremo sono all'interno di spazi metrici che sono quindi anche spazi topologici.

ESEMPIO 1

Un omeomorfismo può “allungare” o “accorciare” a piacere un segmento
Consideriamo degli intervalli  chiusi di r, [a,b], [c,d]. Questi intervalli sono degli insiemi, e sono degli spazi topologici considerando gli aperti generati dalla metrica euclidea. Consideriamo la funzione :

f:[a,b]----->[c,d] così definita:; questa funzione rappresenta una retta, e quindi è continua. La funzione inversa è anch'essa una retta, e quindi è continua. Inutile poi dire  che è una applicazione biettiva. Quindi è un omeomorfismo che trasforma un segmento allungandolo (o accorciandolo).

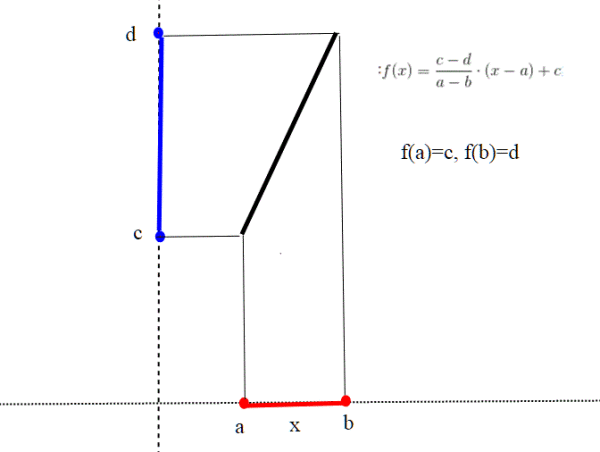
ESEMPIO 2:

Una considerazione preliminare sugli aperti del quadrato.

Se consideriamo un quadrato nello spazio euclideo, esso eredita la topologia del piano, che è fatta di bolle (cerchi nel nostro caso) gli aperti del quadrato sono quelli che si ottengono intersecando tali cerchi(aperti) con il quadrato.

Come aperti avremo dunque segmenti o l'unione di piu segmenti, con dei punti in comune.

Un cerchio è omeomorfo a un quadrato.

Ricordo qui la definizione equivalente di continuità, che ci servirà appena sotto.

Una funzione f: X-->Y fra  due spazi metrici è  continua se e solo se per ogni aperto A di Y,   è un aperto di X.

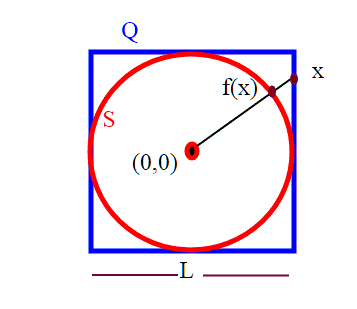
Consideriamo un cerchio S di centro (0,0) e raggio 1,  e il quadrato Q ad esso circoscritto, quindi di lato 2. Siamo nel piano euclideo. Consideriamo la funzione f: Q--->S data da  f(x)=;.Tale funzione è la restrizione della f(x)= considerata in tutti i punti del piano fuorché il punto (0,0).  Attenzione che con x intendiamo la coppia x=(x1,x2), con |x|= la distanza del punto (x1,x2) dall'origine, o se volete, il modulo del vettore x.

Osserviamo intanto che tale funzione    ha modulo unitario; infatti |f(x)|=; quindi tutti i suoi punti stanno sulla circonferenza.

Senza addentrarci in conti analitici che riguardano inoltre le funzioni di due variabili, cerchiamo di  capire un po' intuitivamente questa funzione. Ovviamente è biunivoca: unendo punti diversi sui lati del quadrato, otteniamo punti diversi sulla circonferenza; inoltre la funzione  f: Q--->S  è anche suriettiva; preso un qualunque punto P sul cerchio, prolunghiamo il segmento OP fino a raggiungere il quadrato. Sappiamo poi, per quanto visto nell'articolo precedente sulla topologia indotta, che gli aperti sul cerchio sono gli archi, estremi esclusi; sul quadrato sono invece dei segmenti, o l'unione di segmenti con un estremo in comune. Se adesso consideriamo la controimmagine di un arco su S (definizione di continuità): tale controimmagine è un segmento o un unione di segmenti, che sono gli aperti di Q. Quindi  f è continua.

due esempi di archi (aperti del cerchio) e della loro controimmagine:

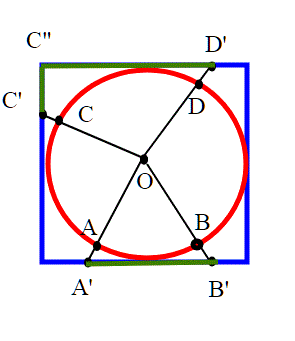
Lo stesso discorso possiamo evidentemente fare per l'inversa ; essa manda gli aperti di Q (segmenti o unione di segmenti) in  archi di cerchio.

Quindi il quadrato è omemorfo al cerchio. Questo mostra che un omeomorfismo può deformare una curva, creando anche degli spigoli.

Il cono è omeomorfo alla sfera senza poli

Che il quadrato sia omeomorfo al cerchio è già una cosa ben strana, ma che il cilindro sia omeomorfo ad una sfera..

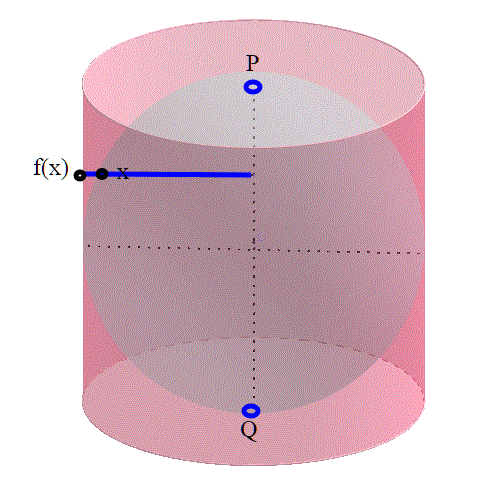
Il trucco sta nel togliere i due poli! La costruzione  grafica dell'omeomorfismo è simile a quello precedente, ma è tridimensionale.

E in sezione:

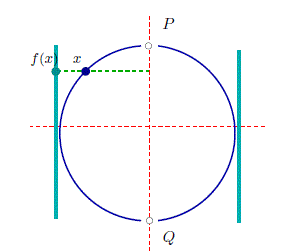
si tratta di proiettare ogni punto della sfera ortogonalmente alla superficie del cilindro; non possiamo farlo in P o Q perchè la funzione avrebbe due valori diversi; ma questo non è possibile per una funzione. Per questo motivo alla sfera sono stati tolti quei due punti.

Quando ho scritto il primo articolo su questi argomenti, avevo promesso ai lettori che sarebbe stato sufficiente conoscere solo i concetti base sugli insiemi, applicazioni, e  relazioni di equivalenza. Voglio mantenere questa promessa ; se esprimiamo la funzione del disegno esplicitamente,(assieme naturalmente alle equazioni di sfera e cilindro) si può dimostrare che f è un omeomorfismo, ma bisogna conoscere le funzioni di più variabili. Chi vuole può fare la dimostrazione, magari la scrive in un commento. Potremmo anche metterla in calce a questo articolo.Vi lascio le definizioni analitiche che servono:

La sfera di raggio 1 ha equazione:; il cilindro C ha equazione:

C=.  Una funzione che esplicita l'omeomorfismo è data da:

f: S----->C ; . Dimostrare che è un omeomorfismo.

 

Siamo partiti dai due buchi sulla sfera e li abbiamo allargati fino ad ottenere un cilindro; un omeomorfismo può quindi allargare dei buchi (anche se non può crearne di nuovi).

Prima di arrivare al nastro di  Möbius, dobbiamo affrontare un altro concetto chiave della topologia: La connessione.