Categorie: Matematica
Tags: geometria Ippocrate di Chio lunule pi greco quadratrice di Dinostrato quadratura del cerchio storia pi greco trisettrice di Ippia
Scritto da: Vincenzo Zappalà
Commenti:43
La storia infinita del pi greco. 3: curve speciali per problemi speciali **
Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"
Torniamo al nostro pi greco che avevamo lasciato al tempo degli egizi. Esso non è ancora giudicato una vera costante, ma il valore di un certo rapporto tra lunghezze o aree. Ma se il pi greco è legato strettamente alla quadratura del cerchio, altri problemi appaiono insolubili per via puramente geometrica.
In pratica, la storia del pi greco si divide quasi subito in due problematiche molto simili, ma essenzialmente diverse: da un lato la determinazione sempre più accurata del suo valore numerico (cosa che ancora oggi continua), dall’altro la possibilità di quadrare secondo le regole che ormai conosciamo bene l’area di un cerchio. La seconda, vuole, in pratica, dire di costruire una lunghezza pari a pi greco attraverso riga e compasso. Abbiamo già accennato come questo risultato non possa essere ottenuto, dato che il pi greco è un numero irrazionale e trascendente, ma, per dimostrarlo con assoluta certezza, molti secoli dovevano passare dai tempi di Euclide.
Prima di dedicarci al miglioramento del suo valore numerico (sempre approssimato, per definizione) analizziamo ciò che si era fatto, già prima di Euclide per ottenere la quadratura del cerchio, ossia riuscire a usare riga e compasso per costruire un quadrato avente la stessa area del cerchio. Questo problema era uno dei tre fondamentali di cui abbiamo già parlato: trisecare un angolo, duplicare un cubo e quadrare un cerchio.
Vedremo che lo studio del primo permise a Ippia (443 - 343 a.C.) di costruire una curva sufficiente allo scopo. Non solo, però... tramite tale curva, Dinostrato (390 – 320 a.C.) riuscì nell’impresa di quadrare il cerchio. Tuttavia, a parte l’insita approssimazione, egli vi riuscì mediante l’utilizzo di una curva “ad hoc” per tracciare la quale non erano assolutamente sufficienti la riga e il compasso. Analogo risultato fu ottenuto anche per la duplicazione del cubo (che affronteremo più avanti, per completezza, anche se non ha veri legami col pi greco).
I tre grandi problemi non potevano essere risolti, ma gli sforzi fatti permisero di costruire nuove curve e fare della geometria una materia sempre più affascinante, ancora prima di essere riscritta attraverso l’algebra.
Quadriamo le lunule
Affrontiamo, prima di tutto, le ricerche di Ippocrate di Chio, un vero genio che sembrava essere giunto a un passo dalla quadratura del cerchio utilizzando la geometria “classica”. Creatore delle lunule che tanto interesse sollevarono anche in Leonardo da Vinci e che divennero la norma in molti motivi architettonici del periodo romanico e gotico, soprattutto nei “rosoni” delle chiese.
 Egli (450-420 a.C.) fu il primo a riuscire a “quadrare” una figura curvilinea, la lunula, appunto.
Egli (450-420 a.C.) fu il primo a riuscire a “quadrare” una figura curvilinea, la lunula, appunto.
Vediamo di costruirla …
Prendiamo il caso più semplice, quello relativo a un triangolo rettangolo isoscele AOB (Fig. 15, a sinsitra).
E’ possibile tracciare il cerchio di raggio uguale ad OA. Limitiamoci all’arco AMB Costruiamo il punto medio H di AB e con raggio uguale ad HA costruiamo l’arco di cerchio ANB. Chiamiamo L l’area compresa tra questi due archi, che rappresenta proprio la lunula (la forma la dice lunga sul nome…).
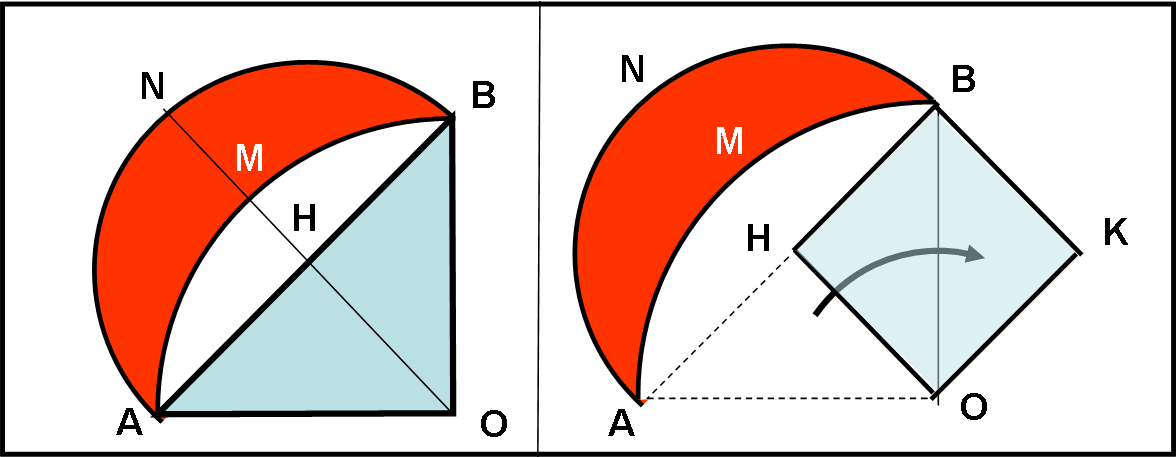
Non è difficile calcolarne l’area, che è data dalla differenza tra l’area del semicerchio ANBH e quella del segmento circolare AMBH.
Area semicerchio ANBH = π AH2/2
Area segmento circolare AMBH = π AO2/4 – Area triangolo AOB.
Chiamiamo a il cateto (AO) del triangolo. Si ricava subito che:
AB = a√2
AH = (a√2)/2
Le aree precedenti diventano:
Area semicerchio ANBH = π a2 2/(4·2) = π a2/4
Area segmento circolare AMBH = π a2/4 – Area triangolo AOB
L’area della lunula L è quindi data da:
L = Area semicerchio ANBH – Area segmento circolare AMBH = π a2/4 - π a2/4 + Area triangolo AOB
In poche parole, l’area della lunula è uguale all’area del triangolo. Dal triangolo al quadrato il passo è brevissimo (Fig. 15, a destra): basta tagliare il triangolo a metà e portarne una metà sotto all’altra e il quadrato è costruito; oppure quadruplicare il triangolo (Fig. 16)
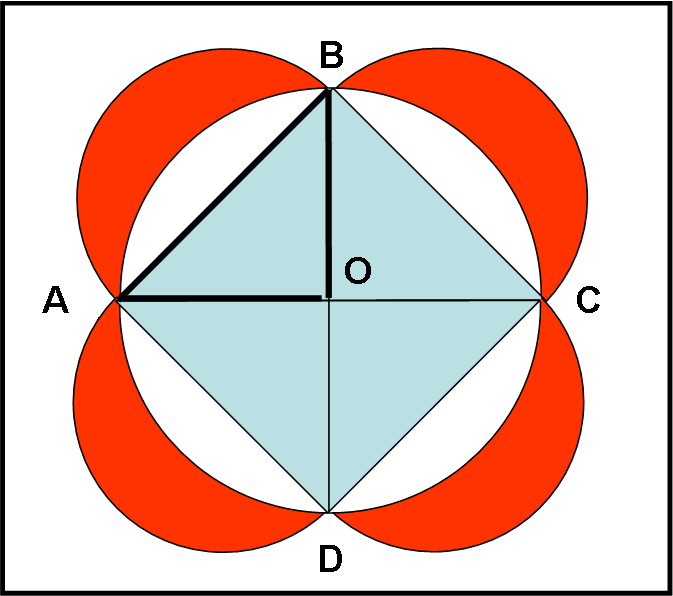
Questo risultato è una vera quadratura, perché dimostra che un’area curvilinea è uguale ad un’area limitata da segmenti di retta che può essere facilmente calcolata.
Ma Ippocrate andò oltre e riuscì a esprimere anche l’esagono regolare (e non solo) attraverso lunule e semicerchi. E’ interessante e facile vedere come… Provate a dimostralo voi. In pratica, si chiede a quali lunule e a quali parti di cerchio è equivalente un esagono regolare.
Diamo di seguito la risposta, ma prima cercate di fare da soli…
Possiamo tranquillamente considerare la metà dell’esagono e quindi limitarci al trapezio isoscele ABCD (Fig. 17 , parte alta).
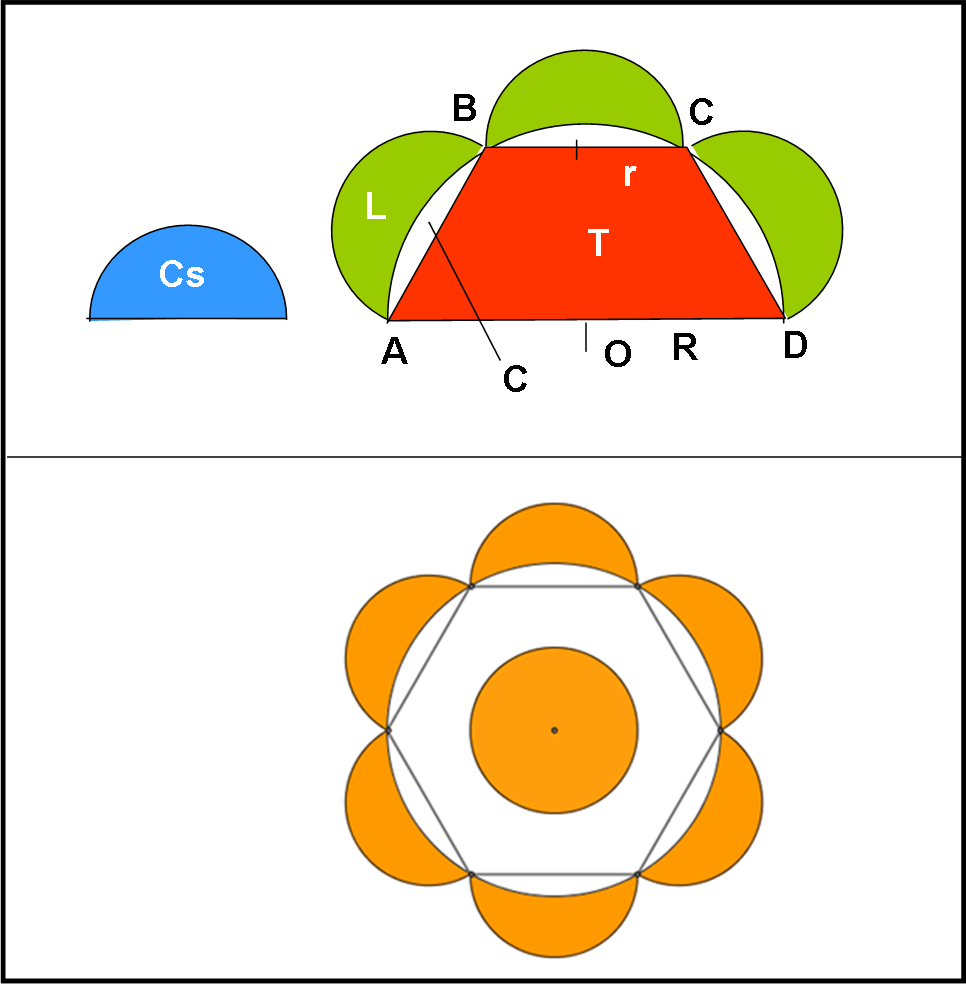
La sua area sia T. L’area del semicerchio (ABCD), costruito sulla sua base maggiore AD, la chiamiamo C. Chiamiamo invece Cs le aree dei semicerchi costruiti sui lati obliqui e sulla base minore (segmenti uguali) del trapezio e L l’area della lunule corrispondenti.
Possiamo scrivere:
3Cs + T = C + 3L
Ma, dato che: r = R/2, vale anche:
4πr2 = πR2
4Cs = C
Se ne deduce:
3Cs + T = 4 Cs + 3L
T = 3L + Cs
Raddoppiando ogni area (parte bassa della Fig. 17) si ha che l’area dell’esagono è equivalente all’area di sei lunule e del cerchio che ha per diametro il lato dell’esagono.
Questo risultato, in cui compare un cerchio, fa pensare a Ippocrate che fosse possibile quadrare anche lui soltanto, ma… non era così.
In ogni modo, notiamo, con una certa attenzione, come l’intera costruzione sia stata fatta solo con riga e compasso… un risultato a dir poco strabiliante nella sua semplicità.
Trisechiamo un angolo: la trisettrice di Ippia
Dedichiamoci, ora, alla trisettrice di Ippia , che prese anche il nome di quadratrice di Dinostrato. Teniamo sempre ben presente che a quei tempi la geometria poteva esprimersi solo attraverso l’uso di strumenti per tracciare linee e curve, non esisteva ancora la loro espressione algebrica e la trigonometria, che noi usiamo normalmente e che useremo anche per descrivere meglio i risultati futuri. Consideriamo, inoltre, che qualsiasi risultato ottenuto con l’ausilio di curve aggiuntive non può essere considerato di geometria “pura”. Questo è proprio il caso della trisettrice che, in seconda battuta, riesce anche a quadrare il cerchio, ma non soltanto con riga e compasso.
Costruiamo la curva per via meccanica, mostrando la Fig. 18.

L’asta AB e quella CD hanno la stessa lunghezza e possono scorrere una dentro l’altra come è mostrato nella figura. La prima descrive un arco di cerchio in senso orario, mentre la seconda trasla in direzione verticale, partendo dalle posizioni AA’ e A’D’. Entrambe si muovono con velocità costante, in modo tale da giungere contemporaneamente nella posizione AB’. Il punto in comune, istante per istante, descrive la traiettoria voluta.
Non era difficile costruire praticamente lo “strumento”, un qualcosa di ben diverso, però, da riga e compasso. Notiamo già una situazione estremamente interessante. Nell’istante finale le due aste coincidono e il punto intersezione risulta indefinito…anche se meccanicamente è facile da indicare. Indicare sì, ma in modo approssimato.
E' interessante presentare un'animazione tratta da Wikipedia che mostra il "lavoro" del meccanismo di Ippia...
Mostriamo, adesso, come viene ottenuto lo scopo iniziale, ossia quello di dividere in tre parti un angolo (Fig. 19)
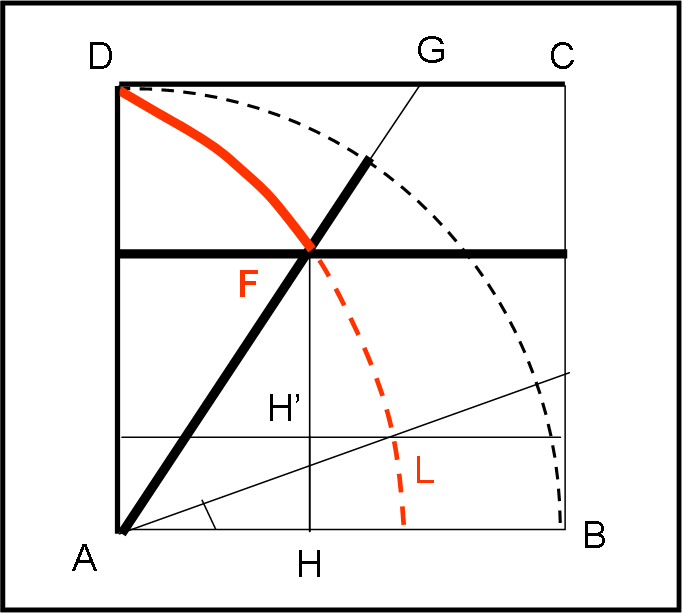
Prendiamo il segmento AD e facciamolo ruotare attorno ad A in senso orario e velocità costante fino a coincidere con AB. Nello stesso intervallo di tempo, con velocità costante, il segmento orizzontale DC trasla, rimanendo parallelo a se stesso, verso il basso fino a coincidere con AB. Il punto F, intersezione, istante per istante, dei due segmenti AD e DC descrive la nostra trisettrice.
Il problema di trisecare un angolo è facilmente risolto. Consideriamo l’angolo FAB e cerchiamo di tracciare una retta che identifichi 1/3 di tale angolo. Per ottenerla basta tracciare da F la perpendicolare ad AB e individuare il punto H; determinare il punto H’ su questa perpendicolare tale che HH’ = 1/3 FH; tracciare la parallela da H’ ad AB e individuare il suo punto d’intersezione L con la trisettrice; la retta AL è quella cercata e individua esattamente un angolo (HAL) pari a 1/3 di quello di partenza.
Il tutto si dimostra facilmente. A causa del moto costante esincrono dell’asta orizzontale e di quella rotante, si può scrivere la proporzione, relativa al punto F:
FAB : π/2 = FH : 1
FH = FAB/(π/2)
La stessa proporzione deve valere per il punto H’. Tuttavia, HH’ = 1/3 FH per costruzione. Ne segue:
LAB : π/2 = FH/3 : 1
LAB = (π/2)FH/3
Sostituendo FH, sia ha:
LAB = (π/2) ((FAB 2/π)/3) = FAB/3
Il gioco è fatto, ma attraverso una curva aggiuntiva e, quindi, il problema di trisecare un angolo rimane insoluto a livello puramente geometrico. Per come è stato diviso l’angolo di partenza è chiaro che esso può essere diviso in n parti con estrema facilità.
Quadriamo “meccanicamente” il cerchio
Facciamo un passo in avanti e vediamo di utilizzare questa curva per quadrare un cerchio, cosa che riuscì a Dinostrato. Per facilitare l’impresa cerchiamo di scrivere l’equazione analitica della trisettrice di Ippia (o quadratrice di Dinostrato).
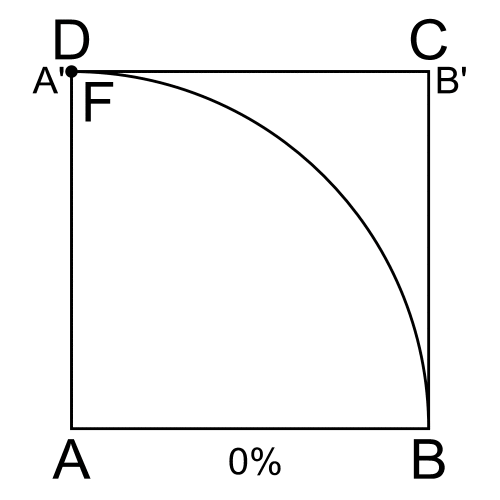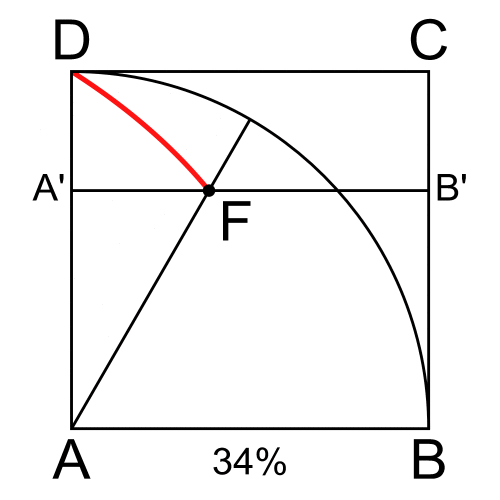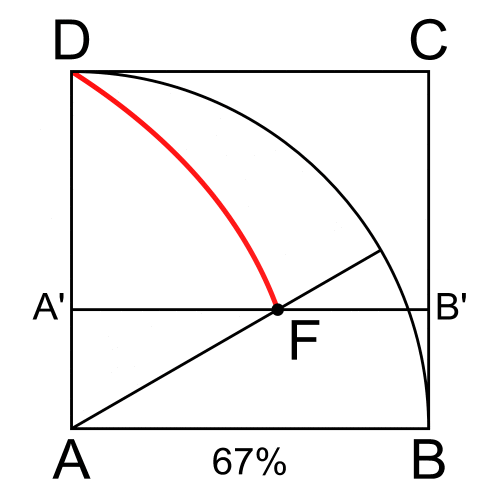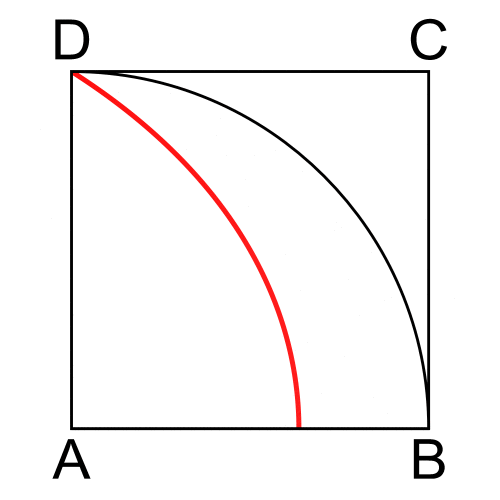
Consideriamo il quadrato ABCD (Fig. 20) e trasliamo il lato DC con velocità costante in un periodo uguale a P per arrivare fino ad AB. Facciamo ruotare il lato AD con velocità angolare ω = π/2P in modo da descrivere 90° nello stesso periodo di tempo. La curva richiesta è il luogo dei punti E intersezione di questi due lati, nel periodo P.
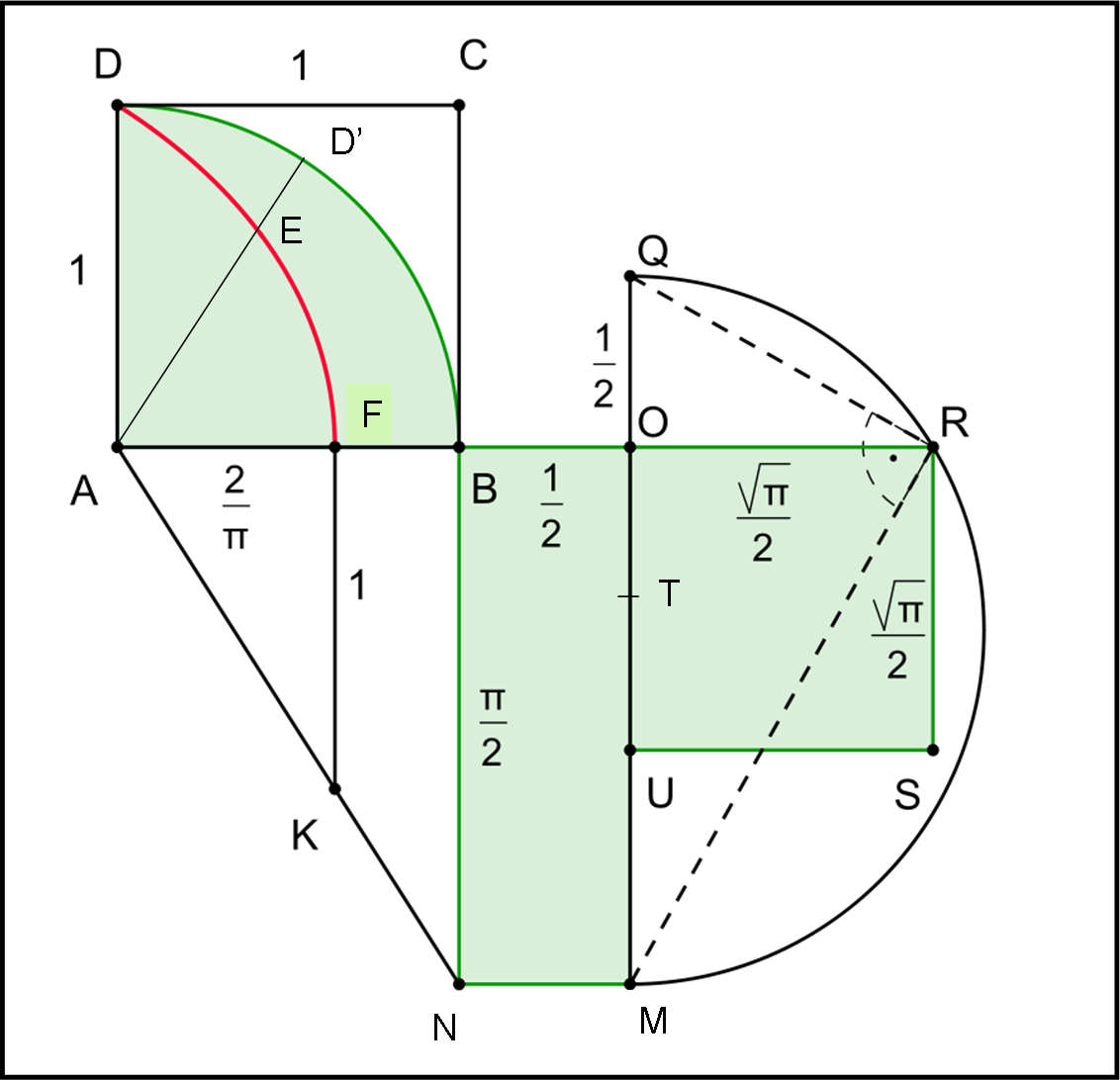
Ovviamente non possiamo limitarci a intersecare due rette, ma dobbiamo fale variare in funzione del parametro tempo, t. Facciamolo variare, considerando come unità il raggio AB = AD e anche il periodo P, abbiamo le due equazioni:
y = 1 – t (spostamento verticale del segmento DC)
y = x tan(α(t)) .... (1) (rotazione del segmento AD)
dove α è BAD’ e vale:
α = π/2 – ωt = π/2 - πt/2 = π(1 – t)/2 = πy/2
Ricaviamo x dalla (1)
x = y/tan(πy/2) …. (2)
A noi servirebbe il valore della curva sull’asse x, ossia per y = 0. Ma, come ci si doveva aspettare, la curva non è definita in quel punto, infatti abbiamo una forma indeterminata 0/0
Non ci resta che provare ad applicare la regola di de l’Hopital.
Se
limy → 0 f(x)/g(x) = 0/0
effettuare le derivate di numeratore e denominatore. Se esiste un limite finito L, esso è uguale al limite di partenza (indeterminato), ossia:
se
limy → 0 f’(x)/g’(x) = L
allora
limy → 0 f(x)/g(x) = L
NB: Uno dei casi più celebri è il limite di sen(x)/x, per x che tende a zero. Facendo le derivate, si ottiene cos(x) che ha come limite 1.
Applichiamola al nostro caso, derivando il numeratore e il denominatore della (2)
limy → 0 (1/((π/2)/cos2(πy/2)) = cos2(πy/2)/(π/2) = 2/π
Ne segue che il punto d’intersezione della trisettrice con l’asse x, F, vale 2/π. La presenza di π conferma l’indeterminazione di questo valore che si risolve solo passando al limite. Comunque sia, la curva di Ippia permette di ottenere “meccanicamente” un segmento pari a 2/π. A quel punto Dinostrato non se lo fa dire due volte e riesce a quadrare il settore circolare ADB.
La sua area è proprio π/4 (raggio = 1), mentre noi abbiamo disegnato con la curva ausiliatrice 2/π. Non è difficile con riga e squadra -e un po’ di Euclide- arrivare a un quadrato di area π/4. Riprendiamo la Fig. 20 e tracciamo da F il segmento FK perpendicolare ad AB. Il segmento FK è preso uguale all’unità. Tracciamo da A la congiungente AK e la prolunghiamo fino a incontrare la perpendicolare ad AB, tracciata da B. Sia N il punto d’intersezione. Dai triangoli simili AFK e ABN si ottiene subito:
AF/FK = AB/BN
(2/π)/1 = 1/BN
BN = π/2
Prolunghiamo il lato AB di un segmento BO uguale a 1/2 e consideriamo il rettangolo BOMN. La sua area è data da:
ABOMN = BN · BO = (π/2)·(1/2) = π/4
Non ci resta che prolungare OM verso l’alto di un segmento OQ = 1/2. Troviamo il punto di mezzo T del segmento QM e tracciamo il semicerchio di raggio QT. Prolunghiamo AB fino a incontrare il semicerchio in R. Consideriamo il triangolo rettangolo (per costruzione) QRM. L’altezza relativa all’ipotenusa QM è proprio RO. Non ci resta che applicare il secondo teorema di Euclide (che ormai conosciamo bene): l’area del quadrato costruito sull’altezza relativa all’ipotenusa è uguale all’area del rettangolo che ha per lati le proiezioni dei cateti sull’ipotenusa. Nel nostro caso abbiamo:
OR2 = OQ · OM = BO · BN = π/4
OR = (√π)/2
OR è proprio il lato di un quadrato la cui area è uguale a π/4, ossia a un quarto del cerchio di raggio AB. Abbiamo ottenuto la quadratura di un cerchio, ma… per farlo oltre a riga e compasso è stata usata una curva ausiliatrice. Pollice verso! D’altra parte il segmento AF è impossibile da determinare se non attraverso un limite: pi greco è sempre pi greco!
Ci piace ricordare che la trisettrice di Ippia o –se preferiamo- la quadratrice di Dinostrato è, probabilmente, la prima curva costruita dopo il cerchio.
Fermiamoci qui…la prossima volta, lasceremo un po’ da parte pi greco, dato che è obbligatorio risolvere anche il terzo grande problema, quello della duplicazione del cubo. Per far ciò parleremo di peste, di oracoli e di nuove curve…
QUI gli altri articoli dedicati all'infinita storia del pi greco






43 commenti
Giorno Enzo, cavolo non riesco ad andare oltre la prima differenza. Spero sia un errore di scrittura altrimenti torno a dormire. Dunque dove dici, riferimento alla figura 15:
Area semicerchio ANBO = π AH2/2
dovrebbe essere: ANBH = π AH2/2
Thanks
grazie Framk... hai pienamente ragione... Ho fatto un bel pasticcio, ingigantitosi facendo copia e incolla...
Ho fatto un bel pasticcio, ingigantitosi facendo copia e incolla...
Spero di aver messo tutto a posto. Abbiate pazienza, ma è un periodo in cui la tranquillità è un po' una chimera....
se trovate errori ditemelo subito, vi prego...
Non lamentarti per un banale errore di scrittura, pensa che ho impiegato il tempo intercorso dalla tua risposta fino ad ora per capire i due passaggi che ottengono l'equivalenza delle due aree................
Proseguo più tardi, vado a studiare il solito moto del proiettile al golf course.
Sì, caro Frank, ma io dovrei fare chiarezza e non creare confusione...
aggiungo, Frank, che prima o poi dovremo fare un quiz sul ... golf!!!!
Magari su un "ACE" realizzato con una traiettoria tale da dover considerare il fatto che g varia in funzione della altezza...
e perchè no?!!!
Eccomi, bene per il golfquiz ma ho l'impressione che non siate ben consapevoli in quale casino vi andate ad infilare. Riguardo alla confusione, vedila così, è stato un buon esercizio di verifica. Prima di chiedere lumi le ho provate tutte anche se era evidente l'errore di battitura e non ti dico la fatica per fare uscire quel 4 al denominatore nei passaggi successivi.
Però oggi la resa è stata altissima uno dei miei migliori score, forse lo "sforzo mentale" prima della gara è servito.
bene! In ogni cosa c'è sempre un lato positivo...
Salve, ho letto con molta attenzione l'articolo in quanto mi interessa particolarmente. Non capisco però l'indicazione di alcune lettere. Per esempio l'ipotenusa del triangolo rettangolo QRM dovrebbe essere QM e non QO, e l'altezza dovrebbe essere OR mentre invece è indicata PO. Infine si dice che è stato determinato il segmento AH, si intende forse quello AF?
caro Pierluigi,
hai perfettamente ragione e ti ringrazio di cuore. Ora dovrebbe essere tutto a posto, ma dammi conferma... Riportare figure dalla carta al PC causa spesso errori di questo tipo... cerco di stare attento, ma... meno male che ci siete voi!
Grazie, adesso quello che vorrei capire in merito alla Trisettrice di Ippia/Quadratrice di Dinostrato è che per determinare appunto il segmento AF si ricorre ai limiti, che ovviamente all'epoca non erano conosciuti. Quindi in che modo si arrivò a formulare la Quadratura (meccanica) del Cerchio?
e, infatti, con riga e compasso è impossibile da ottenere. Si può solo approssimare. Tuttavia, mediante riga graduata, c'era riuscito anche Pitagora, ma non era conforme alle regole. Ne parlerò tra breve...
Rileggendo ancora mi sono accorto di altri piccoli errori, tra cui:
- Questo problema "ero" (era) uno dei tre fondamentali di cui abbiamo già parlato.
- Facciamo ruotare il lato AD con velocità angolare ω = π/2P in modo da descrivere 90° nello "spesso" (stesso) periodo di tempo.
- L'altezza relativa all'ipotenusa "QR" (QM) è proprio RO.
Adesso per cercare di andare a fondo del problema faccio una panoramica basandomi su Wikipedia, sperando di non andare fuori tema. Pi greco si studia praticamente da quando esiste la matematica e nel 1768 Lambert ha dimostrato che è irrazionale. Nel 1882 Lindemann ha dimostrato che è anche trascendente e questo risultato sancisce che è impossibile effettuare la quadratura mediante riga e compasso. Significherebbe che fino al 1881 la quadratura con riga e compasso era possibile?
Tornando ai greci, con riga e compasso non si riusciva e dunque si usò la curva di Ippia che permise a Dinostrato di costruire un quadrato di area equivalente al cerchio. Ma se per farlo occorre calcolare un Limite, in che modo ci riuscirono?
caro Pierluigi,
grazie ancora per i refusi...
Tu dici: "Significherebbe che fino al 1881 la quadratura con riga e compasso era possibile?". Assolutamente no, ma si sperava di riuscirci. In quella data si dimostra l'impossibilità.
Tu dici: "Ma se per farlo occorre calcolare un Limite, in che modo ci riuscirono?". C'è scritto nel testo...
attraverso un sistema meccanico, proprio perché non era ancora possibile ottenere risultati di calcoli trigonometrici o di analisi matematica. Gran parte dei problemi sollevati e risolti meccanicamente dai greci sono risolvibili oggi attraverso l'analisi matematica. Se vai a vedere ciò che sto scrivendo in questi giorni sui cerchi di Archimede, vedrai che sarebbe cosa facilissima calcolare certe soluzioni con metodi "moderni", ma essi diventano molto più complicati solo con l'uso di Talete o poco più... Alcuni, poi, solo attraverso meccanismi creati ad hoc.
L'argomento mi interessa ed appassiona molto, rileggendolo di nuovo mi sono accorto di un altro errore: subito dopo la figura 20 c'è scritto "fale", evidentemente si intende "farle".
Riguardo pi greco, se fosse irrazionale ma non trascendente si potrebbe tracciare con riga e compasso, come ad esempio è possibile fare con √2. Quindi credo voglia dire che si era capito che fosse anche trascendente, ma mancava la dimostrazione, a cui è arrivato Lindemann nel 1882.
Ho riletto anche il procedimento di Dinostrato per quadrare il cerchio usando la Trisettrice di Ippia. Occorre svolgere 10 passaggi per arrivare al quadrato di area π/4, ma il primo consiste nel calcolare un Limite, procedimento che all'epoca non si conosceva. Quindi come è possibile?
ma non è vero Pierluigi! La curva può essere tracciata meccanicamente senza bisogno di calcolare limiti, come è stato riportato nell'articolo... Non riesco a capirti. il limite serve solo per calcolare il valore, ma allora il calcolo non esisteva...
Mi sembra di aver spiegato le varie costruzioni in modo esaustivo... non so più che dire...
Probabilmente vuol dire che Dinostrato ha svolto la quadratura partendo dal punto F, senza preoccuparsi di conoscere la lunghezza del segmento AF indicata nella figura 20. Credo che a confondermi sia la spiegazione del calcolo che porta a 2/π mediante Limite inserita all'inizio del procedimento ma che in realtà non farebbe parte dei passaggi per arrivare all'area del quadrato ORSU.
La Quadratura del Cerchio è trattata anche nell'articolo sulla Spirale di Archimede e in merito alla Cicloide: è meglio se scrivo lì i commenti?
direi di sì...
Purtroppo temo di essermi perso perché non capisco il filo logico della costruzione. Il valore di AF (che è uguale a 2/π) si ottiene mediante il Limite e questo Dinostrato non poteva saperlo. Ma allora come fa a determinare che il segmento BN vale π/2 visto che si ottiene dalla proporzione AF/FK = AB/BN, ossia (2/π)/1 = 1/BN?
Ma, scusa, sapevano benissimo che pigreco era il rapporto tra la lunghezza della circonferenza e il suo diametro... Sono io che non riesco più a capire cosa intendi...
Ripartiamo da zero ignorando i commenti precedenti e analizziamo l'articolo iniziando dalla figura 20, dove si illustra il metodo per arrivare al quadrato di lato OR la cui area è uguale a quella del settore circolare ADB. Tutto il procedimento si basa sul fatto che il segmento AF ha lunghezza π/2, a cui si arriva mediante il Limite. Ma i Limiti ai tempi di Dinostrato non si conoscevano, e infatti al termine dell'articolo viene specificato che: "D'altra parte il segmento AF è impossibile da determinare se non attraverso un limite."
Quindi la domanda è: in che modo Dinostrato ha calcolato la lunghezza di AF?
Sono costretto a ripetermi... AF è stato trovato per via meccanica e non attraverso un calcolo (figure precedenti alla 20). La conoscenza "empirica" di AF non ha bisogno di limiti. L'ultima parte, invece, ne dà una dimostrazione attraverso il calcolo odierno... (nemmeno la tangente era conosciuta).
La domanda è molto semplice: come fa Dinostrato a sapere che il segmento AF (ottenuto meccanicamente) vale 2/π?
Se vuoi tutti i particolari, questo testo ti può essere d'aiuto..
https://www.matematicamente.it/staticfiles/approfondimenti/Magnarelli-Vicentini-trisettrice%20IPPIA.pdf
Grazie, l'ho letto con molto interesse ed attenzione, ma usa la Trigonometria per calcolare valori di angoli e lati, quando abbiamo detto che ai tempi di Dinostrato non si conosceva neanche la tangente. In definitiva vuol dire Dinostrato trovò un metodo elementare per arrivare a calcolare che AF ha lunghezza 2/π. Quale può essere?
La dimostrazione di Dinostrato si basa sulla validità dell'idea che un certo segmento sia medio proporzionale. Come spesso succedeva nell'antica Grecia si lavorava con un ragionamento per assurdo. Lui conosceva il risultato (questo è l'importante della costruzione manuale) e dimostrava che il segmento non poteva essere né più lungo né più corto. Noi ci riusciamo molto più velocemente. Ma, in fondo, poco importa dato che il risultato era quello che veniva messo in evidenza dal meccanismo... Non è facile trovare la dimostrazione "greca", ci provo...
Guarda se questo ti basta, Pierluigi...
https://areeweb.polito.it/didattica/polymath/htmlS/argoment/APPUNTI/TESTI/Apr_03/Cap7.html
Sì, è la dimostrazione di come Dinostrato sia arrivato alla soluzione. Si nota anche che la Trigonometria non basta poi a verificarlo, ma serve appunto ricorrere al Limite.
Un'altra spiegazione si trova qui: <www.latinacittaaperta.info/2020/05/01/sofista-a-chi-ci-sarai/>.
caro Pierluigi,
in generale gli antichi greci NON davano dimostrazioni delle loro proposizioni (vedi proprio i lemmi di Archimede) che ricavavano attraverso meccanismi adatti allo scopo o con ragionamenti che niente avevano a che fare con calcolo come noi lo intendiamo. Ne segue che la dimostrazione di certi enunciati viene data attraverso le tecniche moderne del calcolo. Nel caso della trisettrice, credo che sia stato Pappo a darne la dimostrazione, attribuendola a Dinostrato. In generale, siamo noi che vogliamo dimostrare, mentre loro prendevano come accertate le proposizioni.
Giusto, e comunque le loro formule funzionano, quindi vuol dire che i ragionamenti sono esatti.
Adesso vorrei sapere che procedimento ha svolto Pitagora usando la riga graduata per quadrare il cerchio.
Pitagora o Archimede?
Il 15 agosto alle 19:45 hai scritto che Pitagora ha quadrato il cerchio, però la riga era graduata. Anche questo argomento è molto interessante e vorrei leggere come ha fatto.
Archimede ha usato la sua Spirale, ma facciamo una cosa per volta.
Avevo scritto Pitagora, ma volevo dire Archimede... Pitagora non ha mai quadrato il cerchio, che io sappia...
Quindi vuol dire che Archimede ha quadrato il cerchio 2 volte, con la Spirale e con la riga graduata. Questo secondo metodo come si svolge?
no, no... lui ha trisecato un angolo...
Allora ho capito male, perché il 15 agosto alle 18:27 ho scritto:
"Grazie, adesso quello che vorrei capire in merito alla Trisettrice di Ippia/Quadratrice di Dinostrato è che per determinare appunto il segmento AF si ricorre ai limiti, che ovviamente all'epoca non erano conosciuti. Quindi in che modo si arrivò a formulare la Quadratura (meccanica) del Cerchio?"
e alle 19:45 hai risposto:
"e, infatti, con riga e compasso è impossibile da ottenere. Si può solo approssimare. Tuttavia, mediante riga graduata, c'era riuscito anche Pitagora, ma non era conforme alle regole. Ne parlerò tra breve..."
Il matematico è Archimede e non Pitagora, però l'argomento della discussione è la quadratura del cerchio.
caro Pierluigi, mi sembra che sia stato risolto tutto, a parte il pasticcio che ho fatto io scrivendo Pitagora e parlando di riga graduata. Sai, non sono perfetto e sovente sbaglio, soprattutto in questo momento che devo affrontare ben altri problemi personali. La quadratura del cerchio di Archimede la conosci, così come la quadratura di Dinostrato e la dimostrazione data con i mezzi del tempo. Non so più che fare... Puoi sempre cercare su internet, dato che non capisco più cosa vuoi veramente.
Comunque, domani riesco ad andare quattro giorni in montagna e sarò irreperibile...
Mi ha confuso citare Pitagora al posto di Archimede, ma alla fine è effettivamente tutto risolto. Adesso posso aggiungere il commento nell'articolo che parla di Archimede.
Ciao, torno su questo sempre interessantissimo argomento relativo alla Quadratrice di Dinostrato. Se non ho capito male la sua equazione cartesiana è x = y cot α dove y può avere valori compresi tra 0 e 1 e l'angolo α (EAB in figura) tra 0 e 90° con i 2 termini dipendenti l'uno dall'altro. Una curiosità è che per y = 0.5/α = 45°, il valore di x è 0,5, ossia l'intersezione si trova al centro del quadrato.
Ma in che modo si può calcolare la lunghezza della Quadratrice DF?
caro Pierluigi,
per calcolare le lunghezze delle curve bisogna eseguire un integrale, che nel caso della trisettrice (contiene una cotan) non è banale (oltre che di limitato interesse).
Possiamo allora limitarci a dire che la Quadratrice DF ha una lunghezza compresa tra 1 (lato del quadrato AD) e π/2 (arco DB)?
Il passo successivo sarebbe stato calcolare l'area di ADF.