Questo quiz è stato proposto come introduzione ad un argomento molto importante in topologia: la connessione. Sto mettendo infatti  a punto un articolo in topologia generale su questo argomento. Ma anche in teoria dei grafi la connessione è un argomento importante e prevede anche molte similitudini con la topologia. Riprendo la definizione di grafo data inizialmente qui, in modo un po' più preciso e formale, aggiungendo anche il concetto di connessione e di componente connessa.

Connessione in un grafo.

Se pensiamo alle nostre città del quiz come nodi,e alle strade che le collegano tutte come lati, abbiamo già un esempio di connessione  in   un grafo.

Detto molto più in generale, un grafo è un insieme di punti V detti vertici ( o nodi) mentre E, l’insieme degli spigoli del grafo, è un sottoinsieme del prodotto cartesiano V x V, ossia un insieme di coppie di vertici del grafo. Questa è la definizione rigorosa di grafo; il fatto poi che noi identifichiamo il grafo con il suo disegno non sarebbe molto corretto, ma è senz'altro efficacie.

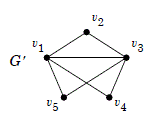
In pratica come nell'esempio il grafo disegnato ha come rappresentazione formale:

V=; vertici

; lati.

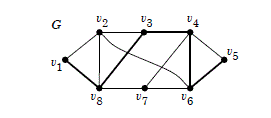
vogliamo adesso formalizzare il concetto di cammino in un grafo. Consideriamo visivamente il percorso in grassetto che  porta da v1 a v5. Possiamo formalizzarlo cosi: il cammino p:v1--->v5 altro non è che la successione di vertici:

p=(v1,v8,v3,v4,v6,v5).

Penso sia un concetto elementare; ebbene diremo che un grafo G è connesso, se comunque presi due vertici u,v esiste un cammino che li collega. Quindi in un grafo connesso tutti i nodi o vertici sono collegati da un cammino. E' proprio come nelle nostre città del quiz. Ci si accorge subito che il fatto di essere collegati , costituisce per due vertici una relazione di equivalenza sull'insieme V dei vertici del grafo G; infatti gode delle tre proprietà:

i) riflessiva (un nodo è collegato a se stesso)

ii) simmetrica ; se u è collegato a v, allora anche v è collegato a u

iii) transitiva: se u è collegato a v, e v è collegato a w, allora u è collegato a w.

Quindi è una relazione di equivalenza. Ma una relazione di equivalenza genera una partizione sull' insieme V. Per dirlo in altre parole, divide le parti del grafo in insiemi disgiunti, e tali che la loro unione dia V.

Ebbene, tali insiemi  costituiscono  le componenti connesse di G

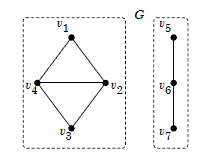
quindi un grafo è l'unione disgiunta delle sue componenti connesse. Al limite le componenti possono ridursi solo ad una. In tal caso il grafo è chiaramente connesso.

Ricordo un poi un risultato dimostrato nel problema dei ponti sui nodi dispari:

"Notiamo un fatto  importante:  In un grafo la somma del numero dei gradi dei nodi è uguale al doppio del numero dei lati, Infatti, ogni lato che unisce due nodi dà un contributo di due alla somma totale dei gradi del grafo."

che si trasforma in:

"ogni grafo contiene un numero pari di nodi dispari. Infatti essendo la somma dei gradi un numero pari, ed essendo  tali gradi pari o dispari, la somma dei pari dà un numero pari, mentre la somma dei dispari dà pari solo se essi sono in numero pari. Notiamo che i nodi dispari possono essere anche zero." Chiaramente questo fatto è valido per qualsiasi componente del grafo, che è essa stessa un grafo.

Ed eccoci arrivati alla soluzione del problema, che poteva benissimo essere dimostrato, pur non sapendo tutte queste cose sui grafi. Lo ha fatto infatti Maurizio in modo unicamente intuitivo, Qui trovate le sue giustificazioni: soluzione Maurizio. Io però non sono contento se non espongo una soluzione di tipo più "matematico".

Soluzione formale del quiz

Togliamo dal grafo G un lato di vertici p ,q;  i gradi di p e q diventano dispari.Si tratta di dimostrare che esiste un cammino che collega p con q , ovvero che p e q appartengono alla stessa componente connessa. E così deve essere, perchè p e q sono gli unici nodi   di grado dispari, e non possono stare in componenti diverse, perchè  altrimenti avremmo una componente con un solo nodo di grado dispari, perché tutti gli altri nodi del grafo G sono di grado pari per ipotesi. Ma abbiamo ricordato sopra che avere un solo nodo di grado dispari in un grafo o in una sua componente è impossibile.

Soluzione di Fabrizio

All'ultimo minuto è arrivata anche la soluzione di Fabrizio che riporto dopo una breve introduzione. La dimostrazione di Fabrizio si basa sul teorema di Eulero, (che è un risultato molto potente)visto in uno degli articoli citati, che riporto qui:

"Un qualsiasi grafo è percorribile se e solo se ha tutti i nodi di grado pari, o due di essi sono di grado dispari; per percorrere un grafo "possibile" con due nodi di grado dispari, è necessario partire da uno di essi, e si terminerà sull'altro nodo dispari. Se invece i nodi sono tutti pari, se si parte da un nodo il percorso finisce su di esso".

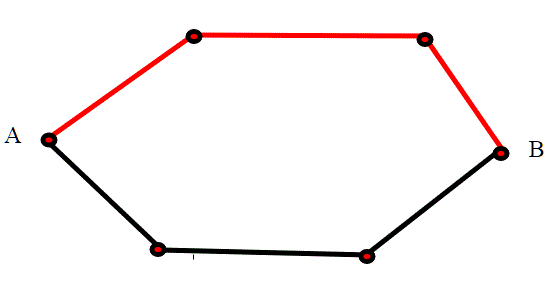
I grafi con tutti i nodi pari sono i cicli Euleriani. Fabrizio dunque afferma che partendo da un qualsiasi nodo si torna in esso. Ma siccome tutti i vertici sono toccati, appartenendo a qualche lato, prendendo un qualsiasi altro vertice, ho due possibili cammini che li uniscono, quindi anche se ne interrompo uno..  riporto il link alla soluzione di Fabrizio  .