Questo articolo rappresenta la soluzione del quiz sulle esplosioni terrestri e solari, ma è soprattutto una trattazione estremamente didattica (addirittura elementare) che ci permette di calcolare quanto richiesto sia matematicamente che graficamente. La Relatività Ristretta è il filo portante, ma l’articolo segue una linea atta a ricordare. Sarà, perciò, utilissimo per chi ha già studiato la RR, a fare riaffiorare concetti depositati nel cassetto della memoria. Per gli altri, speriamo costituisca uno stimolo ad approfondire la conoscenza di ciò che, in modo sorprendentemente semplice, ha posto le basi per la grande rivoluzione scientifica che sarà la Relatività Generale.

Prima di iniziare dobbiamo ricordarci almeno due concetti fondamentali, che sono proprio le basi di tutta la RR.

1) Le coordinate di un EVENTO, in un certo sistema di riferimento (x,t) inerziale, sono collegate alle coordinate (x’,t’), in un altro sistema di riferimento inerziale, in movimento con velocità v rispetto al primo, mediante le formule che descrivono la trasformazione di Lorentz.

t’ = γ(t – vx/c²)

x’ = γ(x – vt)

dove γ = 1/(1 – v²/c²)^1/2

2) Analogamente, si possono scrivere le differenze di coordinate nei due sistemi

Δt’ = γ(Δt – vΔx/c²)             …. (1)

Δx’ = γ(Δx – vΔt)                …. (2)

Utilizzando la (1) con i dati del quiz si ricava velocemente la differenza di tempo richiesta:

v = 0.8

Δx = distanza spaziale tra i due eventi nel sistema Terra-Sole, ossia distanza tra il Sole e la Terra = 8.3 minuti luce

Δt = distanza temporale tra i due eventi nel sistema Terra-Sole = 2 minuti

Nel sistema astronave in movimento dalla Terra al Sole si ha:

Δt’_TS = γ(Δt – vΔx/c²) = (2 – 0.8 (8.3))/0.6 = - 7.73 minuti

Invertendo la direzione dell'astronave, cioé facendola andare dal Sole alla Terra, la velocità v è uguale e contraria al valore precedente, ossia vale -v e quindi  si ha la formula:

Δt’_ST = γ(Δt + vΔx/c²) = (2 + 0.8 (8.3))/0.6 = 14.40 minuti

Tutto qua… ma, abbiamo subito un risultato abbastanza interessante  dovuto alla relatività della simultaneità.

Nel primo caso la differenza di tempi è negativa, il che implica che nel sistema astronave avviene prima il brillamento e dopo l’esplosione del vulcano. Ripeto ancora che questo NON VUOLE DIRE che l’astronave vede prima il brillamento rispetto al vulcano. Il vedere i due fenomeni comporta altri due eventi del tutto differenti (come spieghiamo nei paragrafi che seguono).

Molto utile per i meno preparati è la costruzione grafica del diagramma di Minkowski dei due casi, prendendo come sistema fermo sia quello Terra-Sole che quello dell’astronave, sia in una direzione che nell’altra. Proviamo a farlo, andando avanti per piccoli passi. I più bravi saltino pur questa lezioncina.

Iniziamo disegnando il sistema Terra-Sole come sistema fisso. Ricordiamo ancora che un sistema di riferimento  rappresenta tutto lo spaziotempo, dopo aver sincronizzato tutti suoi orologi e aver fissato l’unità di distanza. L’orologio della Terra e del Sole segnano sempre lo stesso tempo. Tuttavia, affinché un’immagine dell’orologio del Sole arrivi sulla Terra si devono aspettare gli 8.3 minuti necessari alla luce. Ciò dimostra ancora perfettamente che eventi simultanei hanno lo stesso tempo ovunque nel sistema, ma anche che il poter vedere qualcosa da un punto diverso comporta un certo ritardo dovuto alla lentezza della velocità della luce. Non mischiamo, quindi, i due effetti.

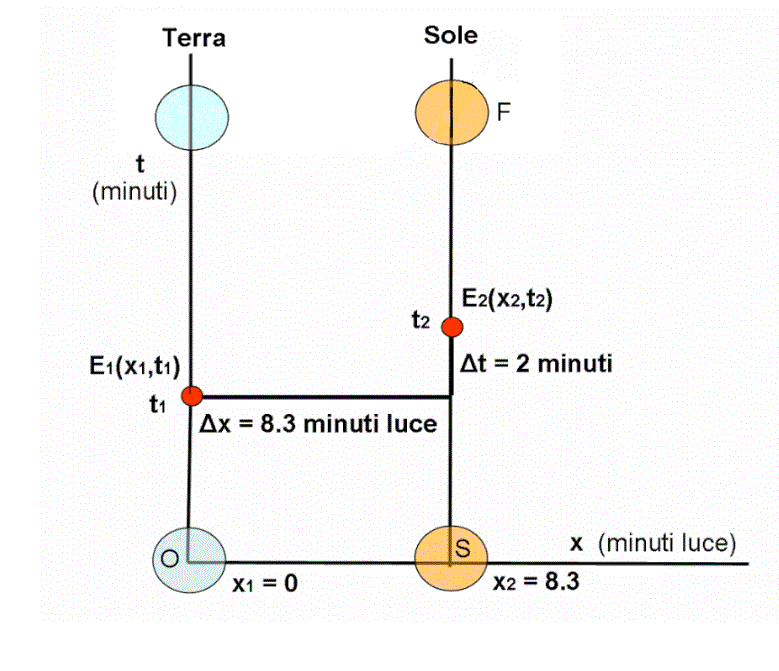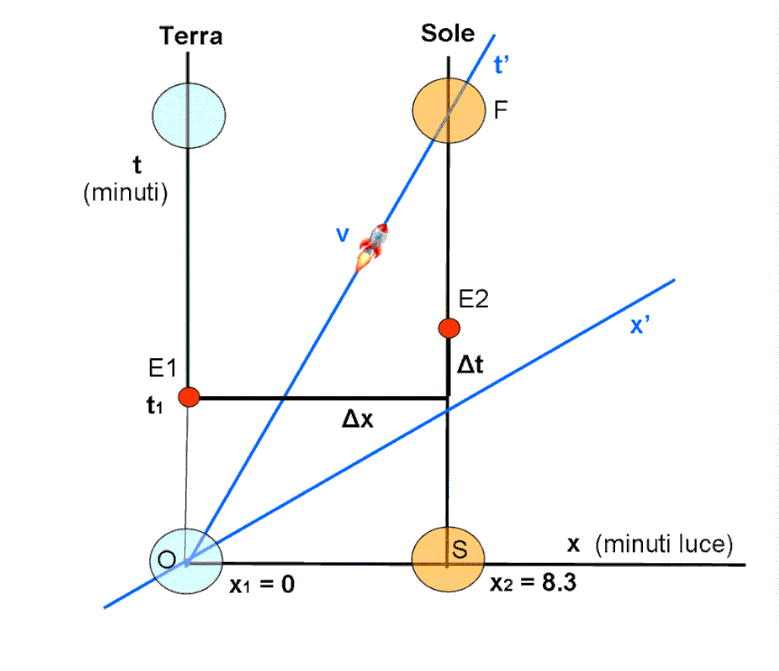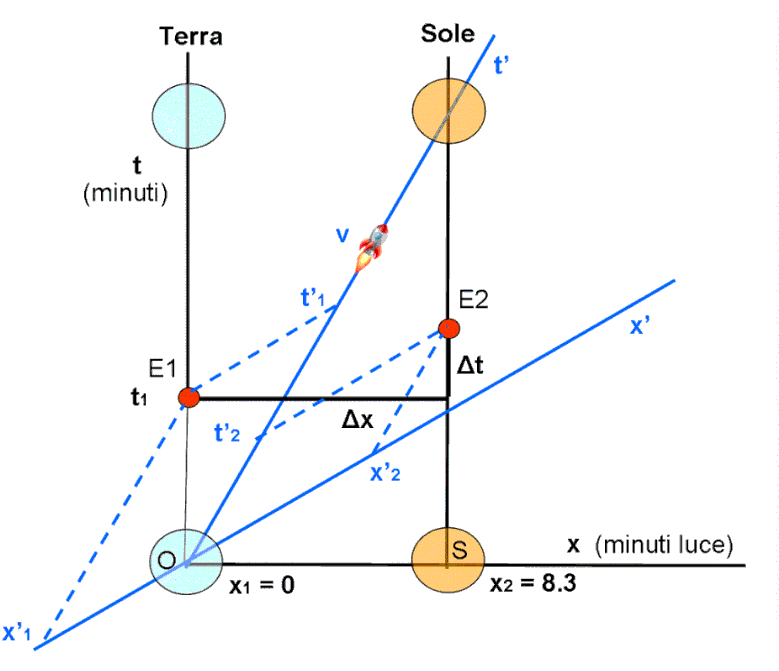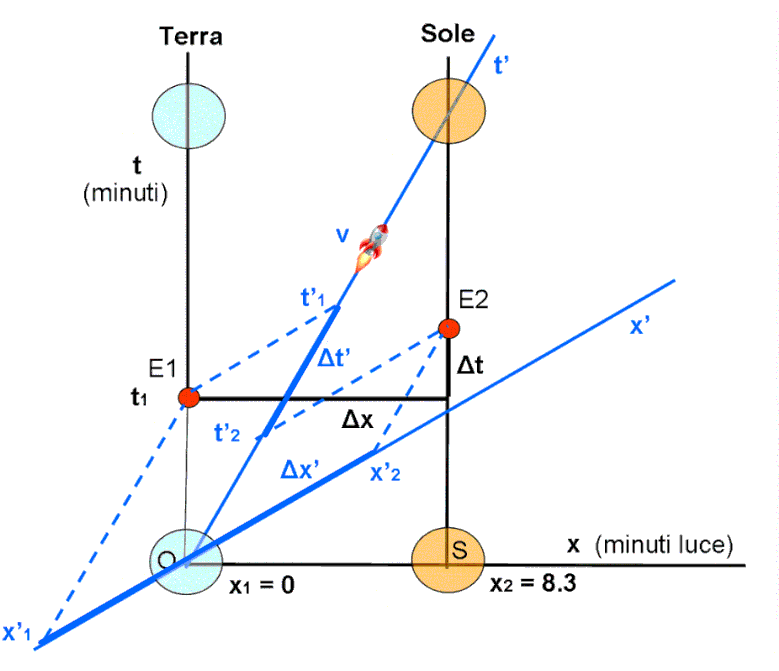
Gli assi sono x (orizzontale), rappresentante lo spazio, e t (verticale), rappresentante il tempo. Ogni punto od oggetto del sistema che è considerato fermo non può muoversi lungo l’asse x e quindi il suo moto avviene solo lungo una parallela a t. La verticale definita in questo modo è la linea di Universo dell’oggetto in questione, considerato fermo, come, in realtà, vogliamo considerare la Terra e il Sole. Ecco quindi la semplicissima Fig. 1, con le due rette verticali della Terra e del Sole che si muovono in perfetto accordo (il tempo è lo stesso per entrambi), mantenendo una distanza pari a 8.3 minuti luce. Per “risparmiare” linee, abbiamo messo la Terra proprio lungo l’asse del tempo, ma, per le caratteristiche del sistema, qualsiasi altro parallela  sarebbe andata benissimo: l’importante è mantenere la stessa distanza tra la linea della Terra e quella del Sole.

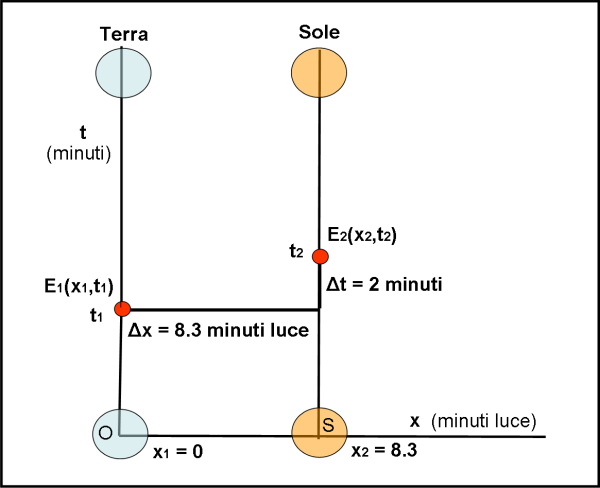
Durante il loro tragitto verso l’alto, in cui si mantiene sempre la simultaneità data dalla retta orizzontale (retta di tempo costante), sulla Terra esplode il vulcano. Questo fenomeno rappresenta un evento E₁ dello spaziotempo, che ha certe sue coordinate rispetto all’origine e agli assi scelti. Nel caso della figura le sue coordinate sono x₁ e t₁ (x₁ = 0). Dopo due minuti (segnati perfettamente sia dall’orologio della Terra che da quello del Sole), il Sole ha un brillamento che rappresenta l’evento E₂, di coordinate x₂, t₂. Il valore di x₂ non è altri che la differenza tra la x costante del Sole e quella costante della Terra, ossia x₂ - x₁ che, per la scelta dell’origine degli assi, non è altro che x₂, ossia la distanza Terra-Sole, pari a 8.3 minuti luce.

I valori t₁ e t₂ sono invece lasciati liberi nel quiz e quindi possono essere scelti ovunque lungo le linee di Universo di Terra e Sole. L’importante è che la differenza temporale tra i due sia di due minuti. Intervallo di tempo misurato, ovviamente, sia dall’orologio della Terra che da quello del Sole.

Si ha subito la conferma che sia Δx che Δt non variano al variare della scelta dell’origine degli assi. A questo punto, pur avendo scritto cose banalissime, abbiamo una perfetta idea delle condizioni di partenza del nostro quiz, profondamente didattico.

Possiamo anche permetterci di costruire facilmente gli eventi “Terra che vede il brillamento solare” e “Sole che vede il vulcano terrestre”, anche se del tutto estranei al quiz, in Fig. 2.

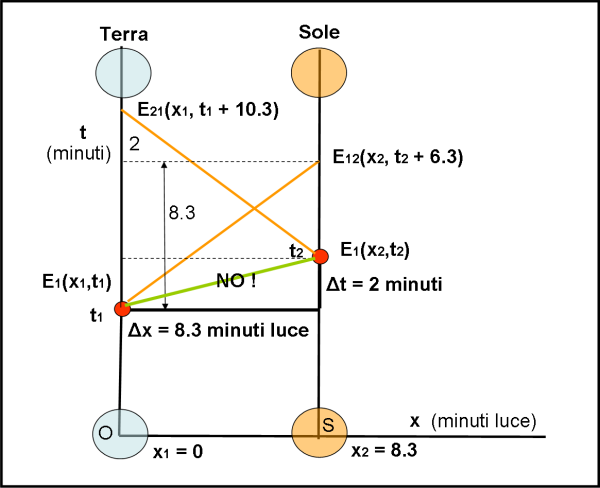
Per come sono state scelte le unità di misura dei due assi (minuti luce (x) e minuti (t)), la linea che rappresenta l’informazione luminosa forma un angolo di 45° con i due assi, ossia essa percorre 8.3 minuti luce in 8.3 minuti.

Possiamo facilmente rappresentarli nella figura. E₁₂ è l’evento che rappresenta la visione del vulcano sul Sole ed E₂₁ è l’evento che rappresenta la visione del brillamento sulla Terra. Questi due eventi devono, ovviamente, mantenere la x della Terra e del Sole (essi non si muovono spazialmente), ma hanno tempi diversi, calcolabili immediatamente attraverso la figura. Il tempo che la luce impiega per arrivare dalla Terra al Sole e viceversa è uguale a 8.3 minuti, da cui segue che E₂₁ ha una coordinata

t₂₁ = t₁ + 2 + 8.3 = t₁ + 10.3

Mentre la coordinata tempo del fenomeno vulcano visto dal Sole è:

t₁₂ = t₂ + 6.3

Ne segue che sulla Terra la differenza di tempo tra il fenomeno vulcano e la visione del brillamento solare è di:

t₂₁ – t₁ = 10.3 minuti

Mentre sul Sole la differenza tra brillamento e visione del vulcano è:

t₁₂ – t₂ = 6.3 minuti

Ovviamente, E₁₂ ed E₂₁ continuano ad avere una differenza di tempo uguale a 2 minuti nel sistema Terra-Sole, per come è stata tracciata la linea percorsa dalla luce (45°).

Abbiamo solo giocato, dicendo cose banalissime ed elementari, tuttavia sufficienti a divertirci con eventi, sistemi di riferimento e velocità della luce. Fino a questo punto è chiaro che non è stata toccata la relatività ristretta. Possiamo, però già puntualizzare una cosa estremamente importante: niente e nessuno potrà mai vedere “in diretta” i due eventi E₁ ed E₂, ossia muoversi in modo che il suo tragitto passi per la Terra quando esplode il vulcano e per il Sole (a parte il caldo) quando avviene il brillamento. Unendo E₁ con E₂ si ha infatti una linea che percorre uno spazio (8.3 minuti luce) in solo due minuti di tempo. Per poterci riuscire bisognerebbe andare decisamente più veloci della luce e se questo andava bene per Galileo, non va più bene per Einstein!

Noi siamo abituati ad avere a che fare con sistemi di coordinate in cui gli assi x e y (o x e t nel caso dello spaziotempo) sono tra loro ortogonali. Tuttavia, possiamo anche usare assi inclinati di un angolo qualsiasi tra loro. Determinare le coordinate di un punto (o di un evento) non è , comunque, un compito difficile, dato che basta condurre le parallele agli assi, passanti per il punto o l'evento.

Proviamo a farlo nel caso dei nostri due eventi E1 ed E2, considerando come nuovi assi x' e t'. Ce lo illustra la Fig. 3.

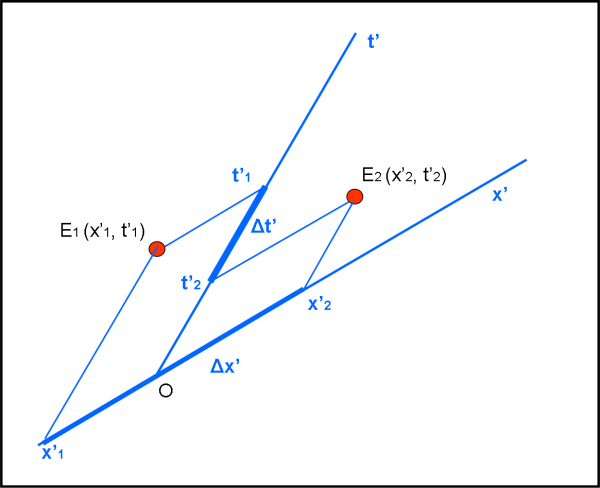
Ovviamente, lo spaziotempo rimane sempre lo stesso, così come i due eventi E₁ ed E₂  e non ci vuole molto a determinare  i nuovi valori di Δt' e Δx'.

Al di là dei valori numerici (tutto dipende dalle unità di misura usate sui nuovi assi), possiamo già notare un risultato piuttosto interessante: sull’asse t’, l’evento E₂ avviene prima dell’evento E₁.

Va bene… trafficando un poco con i sistemi di riferimento, ci siamo divertiti a richiamare concetti e costruzioni grafiche estremamente semplici, ma che ci prendono per mano e ci portano direttamente alla rappresentazione dello spaziotempo di Minkowski. Cosa ci resta da fare, infatti?

Nient’altro che trasformare le coordinate di un sistema di riferimento nelle coordinate di un altro, che sia legato al primo attraverso la trasformazione che è alla base di tutta la RR, ossia quella di Lorentz. Una trasformazione che in pratica ruota gli assi cartesiani e dilata l’unità di misura. Qualcosa di molto simile a quanto fatto nella Fig. 3.

Torniamo perciò all’inizio di questo articolo e, nello spaziotempo in cui erano rappresentati il Sole, la Terra e i vari eventi, inseriamo un nuovo sistema di coordinate (ma lo spaziotempo rimane quello che è) non qualsiasi, ma che si muove rispetto al primo con una velocità v. Attenzione! per non "stringere" troppo le figure è stata usata una velocità qualsiasi, minore di 0,8c, dato che i valori numerici esatti li abbiamo già trovati all'inizio. Ci interessano soprattutto i concetti!

La trasformazione di coordinate rappresenta perfettamente in modo grafico ciò che descrive la trasformazione di Lorentz e si costruisce in modo piuttosto semplice, come si può trovare  spiegato nell’approfondimento  (capitolo: Il signor Lorentz si arrabbia). Variando la velocità, varia l’angolo tra gli assi del sistema fisso e quello in movimento e  non è nemmeno difficile costruire una certa curva (l’iperbole di calibrazione) che permette di determinare graficamente come vari l’unità di misura sui nuovi assi. Gli assi x’e t’ si avvicinano sempre di più tra loro e mantengono lo stesso angolo rispetto alla linea che percorre la luce.

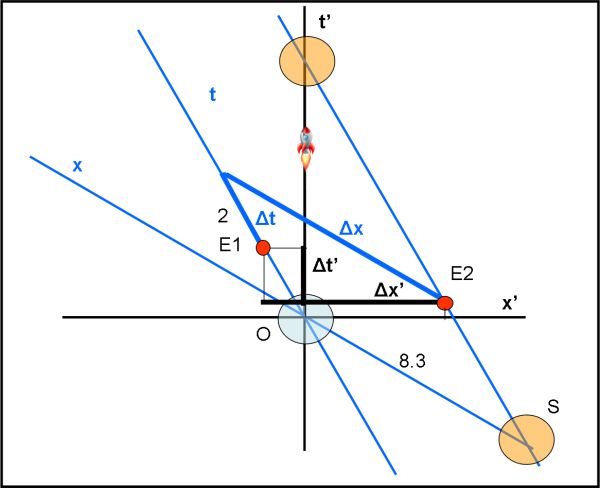
Passiamo, allora, alla Fig. 4, dove gli eventi restano quelli che sono nello spaziotempo, ma viene inserito il nuovo sistema di coordinate relativo a un’astronave che viaggi tra la Terra e il Sole (o viceversa) con una certa velocità v. Ciò, in pratica, equivale a inserire nel diagramma di coordinate ortogonali (sistema fermo) x e t, un nuovo sistema di coordinate x' e t', simile a quello di Fig. 3  (sistema in movimento).

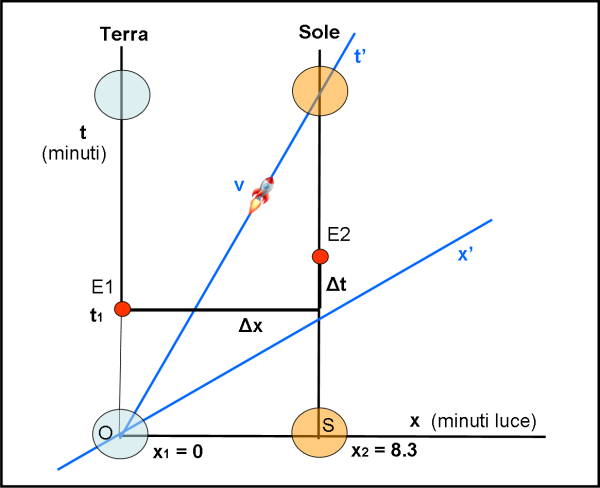
La figura si complica un po’, ma ormai sappiamo benissimo come agire in entrambi sistemi. Basta infatti determinare le coordinate rispetto al sistema in movimento, seguendo quanto fatto in Fig. 3, come è rappresentato in Fig. 5.

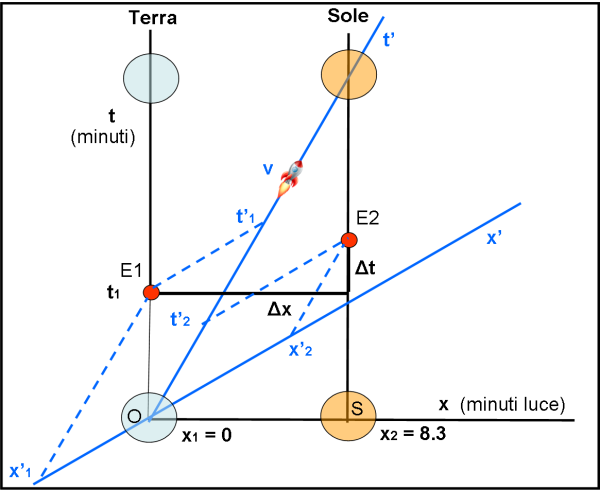
Questo semplice operazione dimostra la base di tutta la relatività ristretta: ciò che è simultaneo in un sistema (eventi con la stessa t, ossia scelti lungo una linea parallela all’asse x) non lo è più nell’altro, dove lo stesso tempo t’ si ha su una linea parallela all’asse x’. Per determinare l’unità di misura sui vari assi basta ricordarsi la Fig. 6, dove, costruendo l’iperbole di calibrazione, è facile evidenziare e toccare con mano la tanto celebre dilatazione del tempo, che Minkowski ha reso palpabile su un grafico a due dimensioni (tanto di cappello!). Per saperne di più basta andare qui e ci si accorge della semplicità del diagramma di Minkowski.

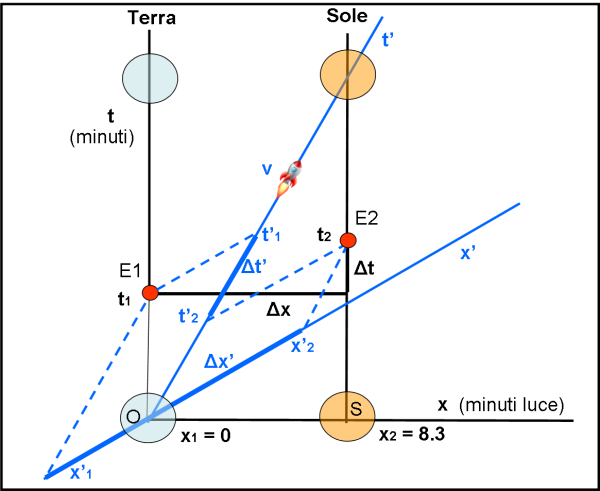
In Fig. 7 è immediato evidenziare il segmento blu più spesso che fornisce graficamente il valore cercato di Δt’ (e anche Δx’).

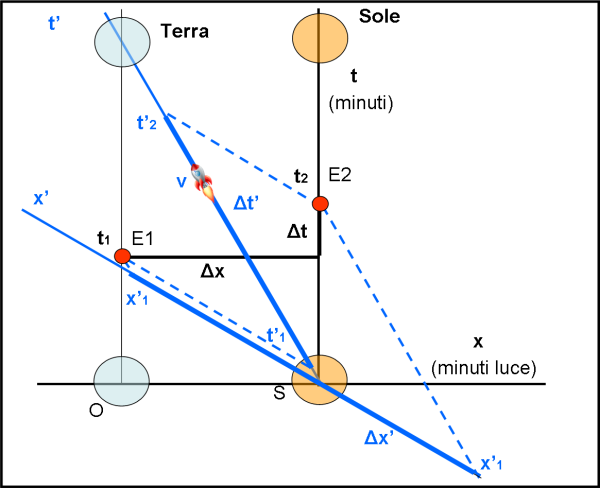
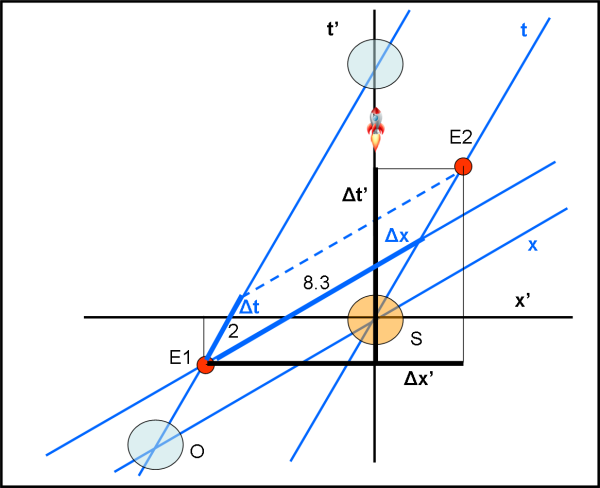
Bene, a questo punto è facile e intuitivo proseguire, invertendo la rotta dell’astronave (Fig. 8), il che equivale a sostituire  -v a v, ossia ribaltare la figura rispetto all'asse del tempo t. Questa volta, ovviamente, il punto di partenza è il Sole e non la Terra. Ovviamente, i tempi e i loro intervalli cambiano (gli eventi non si muovono!), ma il tutto è risolvibile graficamente seguendo le regole appena descritte.

Non è nemmeno difficile considerare come fisso il sistema di riferimento dell’astronave e vedere muoversi il sistema Terra-Sole (che mantiene ovviamente le distanze temporali e spaziali tra gli eventi). Il risultato finale, tuttavia, tenendo conto delle variazioni delle unità di misura, non può cambiare (Fig. 9 e 10): questa è la RR, bellezza!

 

Non ho voluto costruire passo per passo queste due ultime figure, lasciando ai meno esperti il piacere di arrivarci da soli, seguendo quanto detto precedentemente. L’importante è non spaventarsi a  rappresentare il Sole e la Terra come due corpi che si muovono all’unisono nello spaziotempo lungo linee inclinate…

Rivediamo a conclusione di questa parte, con una semplice animazione  progressiva,i passaggi della costruzione che ci ha consentito di rappresentare (Fig. 7) i valori di   Δt’ e di Δx’  per l'astronave in viaggio dalla Terra al Sole.

 

L’idea è di fermarci qui… tuttavia, una volta impostata e capita la situazione possono essere materializzate e calcolate molte altre situazioni interessanti come le coordinate degli eventi “visione” nel nuovo sistema; il punto d’incontro di due astronavi che partano insieme dalla Terra e dal Sole; e tante altre… No, non faremo tanti quiz, ma, aspettando anche vostri suggerimenti, cercheremo di trattarli un po’ alla volta. La RR avrà sempre meno segreti…

**********************************************************************************************************

APPENDICE

Mentre ci pensate, giusto per ribadire i concetti appena espressi, ciò che si propone è un piccolo esercizio, sul quiz.

Innanzitutto una prima immagine che confronta l'astronave in rotta dalla Terra al Sole, con il sistema terricolo.

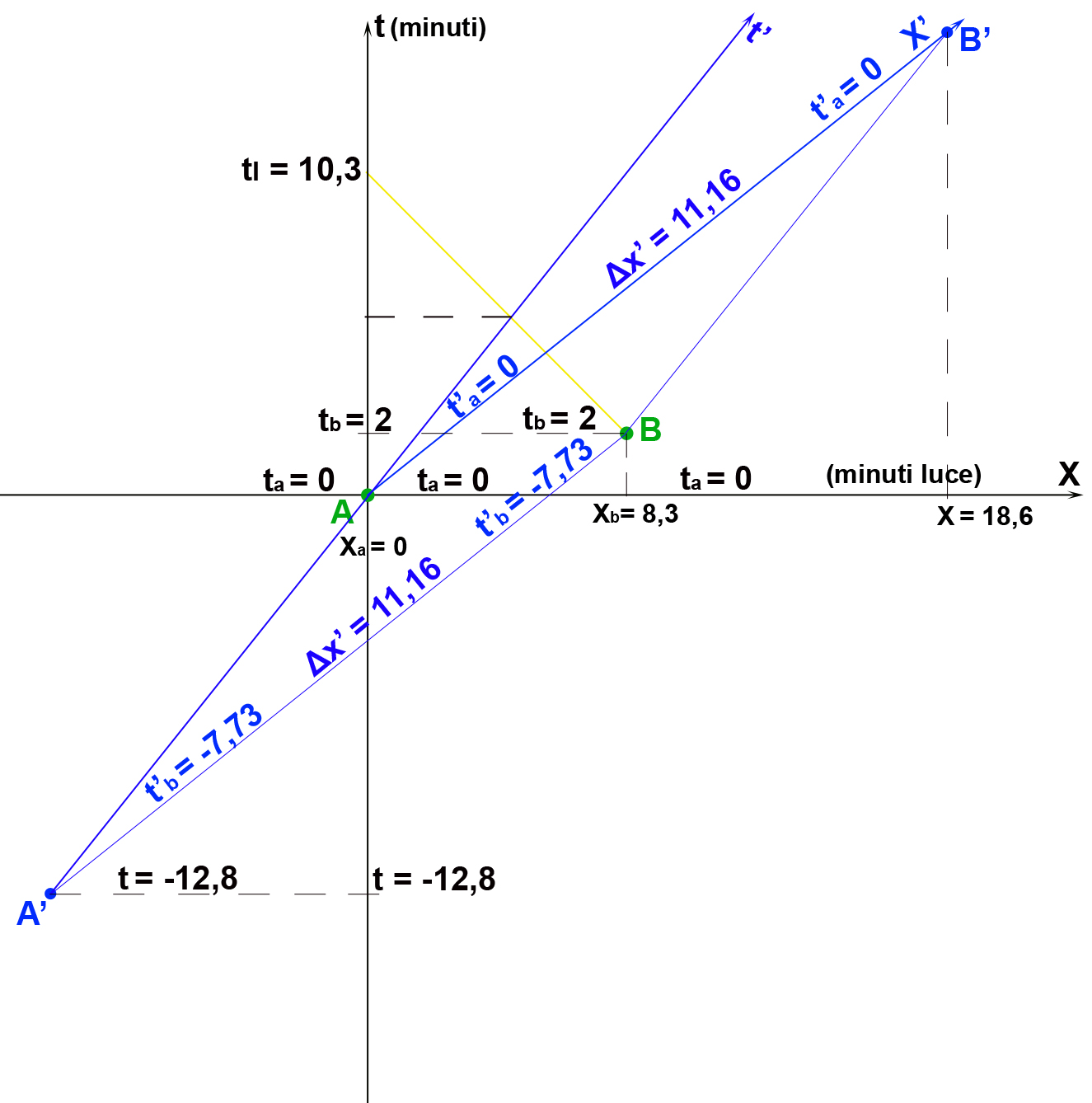
Per confrontare l'intervallo di tempo che separa i due eventi (A eruzione vulcano e B eruzione solare) misurato dal sistema terricolo con quello dell'astronave, è possibile usare le trasformazioni di Lorentz.

Per i terricoli:

ta= 0; tb= 2; xa = 0; xb = 8,3 e la velocità dell'astronave rispetto alla luce è 0,8c.

Innanzitutto si ricava il valore del fattore di Lorentz:

γ = 1/√(1- v²/c²) = 1/√(1- 0,8²) = 1/0,6

Dopodiché si ricava l'intervallo di tempo Δt’, che separa i due eventi secondo l'astronave, ricordando che:

t’ = (t – vx) γ

t'a = (ta – vxa) γ e t'b = (tb – vxb) γ

Δt’ = (t'b – t'a) = (tb – vxb) γ - (ta – vxa) γ

Δt’ = (tb – vxb -ta + vxa) γ

Δt’ = ((tb -ta) -v (xb - xa)) γ

Δt’ = ((2 -0) -0,8 (8,3 - 0))/0,6

Δt’ = (2 -(0,8 (8,3))/0,6 =

Δt’ = (2 -(0,8 (8,3))/0,6 = -7,73 minuti

Il valore trovato è negativo solo perchè per l'astronave l'evento B avviene prima dell'evento A, per cui tb è minore di ta.

Infine usando le trasformazioni di Lorentz si ricava anche l'intervallo di spazio Δx’, ricordando che

x’ = (x – vt) γ

x'a = (xa – vta) γ e x'b = (xb – vtb) γ

Δx’ = (x'b – x'a) = (xb – vtb) γ - (xa – vta)

Δx’ = (xb – vtb - xa + vta) γ

Δx’ = ((xb- xa) – v (tb -ta)) γ

Δx’ = ((8,3- 0) – 0,8 (2 -0)) /0,6

Δx’= (8,3 – (0,8 (2)) /0,6 = 11,16 minuti luce

Giusto per conferma nella figura intervallo di tempo Δt’ corrisponde a un intervallo misurato sull'asse del tempo t di -12,88 minuti.

Visto dal sistema di riferimento del terricolo, il tempo dell'astronave appare dilatato, ossia:

Δt’ = Δt 1/γ = -12,88 x 0,6 = -7,73

Inoltre per il sistema del terricolo, anche lo spazio dell'astronave appare contratto (x =18,6) :

Δx’ = Δx 1/γ = 18,6 x 0,6 = 11,16 minuti luce.

I risultati ovviamente coincidono!

Infine per i due sistemi di riferimento cambiano i tempi e le distanze, ma non cambia la distanza spaziotemporale tra i due eventi, ossia:

T² – X² = T'²- X'²

T² – X² = 2² – 8,3² = -64,89

Il segno meno indica che i due eventi non possono essere connessi tra loro, ossia uno non può essere la causa dell'altro (d'altronde in 2 minuti la luce, ossia l'informazione, non può certo percorrere 8,3 minuti luce).

T'²- X'² = -7,73² - 11,16² = -64,89

Come volevasi dimostrare la distanza spaziotemporale tra A e B è un invariante, ossia è uguale per tutti i sistemi di riferimento (attenzione che i valori riportati sono approssimati alla seconda cifra decimale, ma se si evitano le approssimazioni il risultato è preciso, ossia -64,89).

Un'ultima veloce considerazione: nella figura è stata indicata anche la luce che parte da B e raggiunge la Terra al tempo t= 10,3 minuti (2 + 8,3), mentre raggiunge l'astronave dopo circa 3,4 minuti dall'evento A (nella figura A visto dall'astronave avviene al tempo t' =0).

Lo stesso ragionamento si può fare per l'astronave rossa che viaggia dal Sole verso la Terra, ma nelle trasformazioni di Lorentz, la velocità cambia di segno.

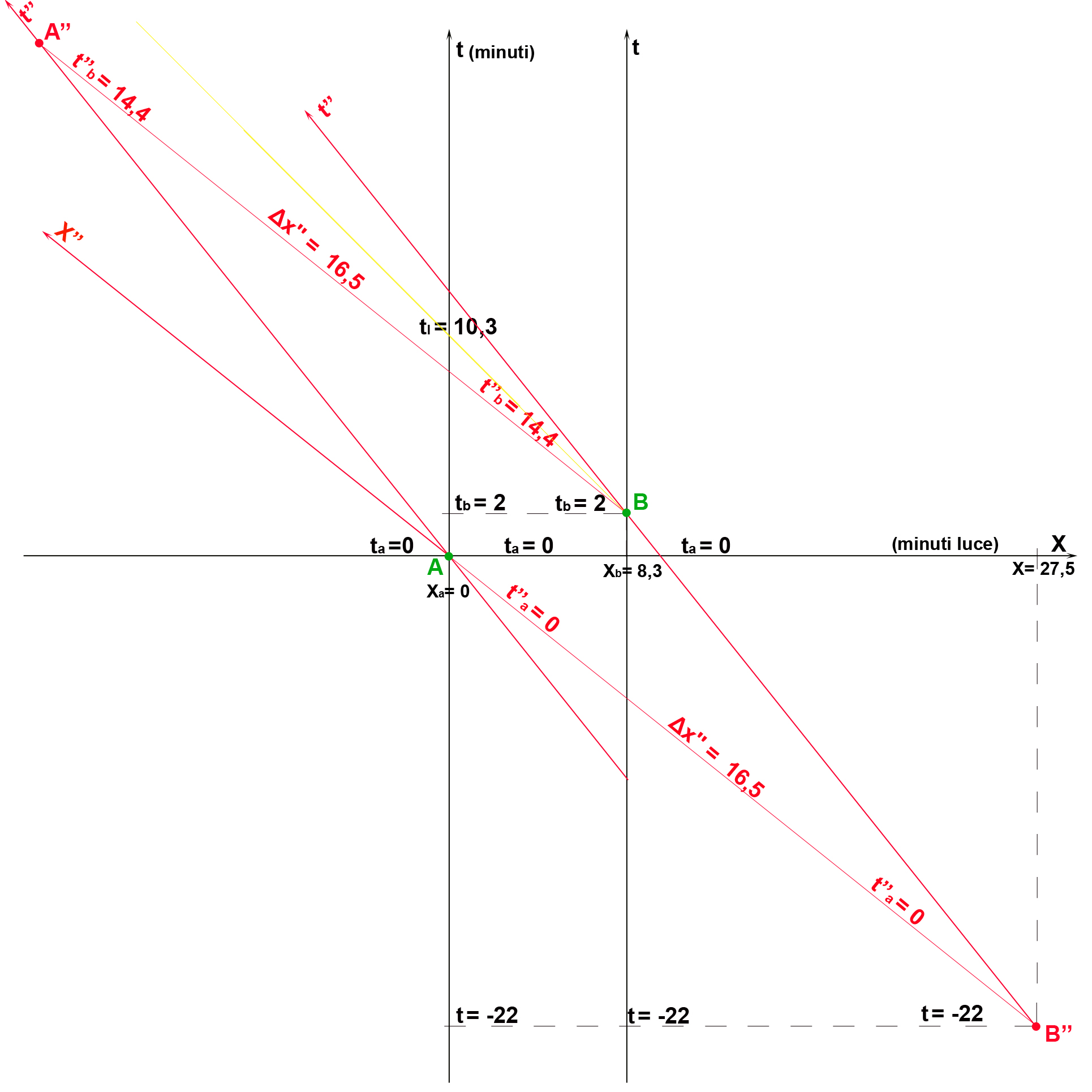
t'' = ((t - (-vx)) γ

t'' = (t + vx) γ

t''a = (ta + vxa) γ e t''b = (tb + vxb) γ

Δt'' = (t''b – t''a) = (tb + vxb) γ - (ta + vxa) γ

Δt'' = ((tb -ta) + v (xb- xa)) γ

Δt'' = ((2 -0) + 0,8 (8,3- 0)) /0,6

Δt'' = (2 + 0,8 (8,3)) /0,6

Δt'' = (2 + 0,8 (8,3)) /0,6 = 14,4 minuti

x'' = (x + vt) γ

x''a = (xa + vta) γ e x''b = (xb + vtb) γ

Δx'' = (x''b -x''a) = (xb + vtb) γ - (xa + vta) γ

Δx'' = (xb + vtb - xa – vta) γ

Δx'' = ((xb -xa) + v (tb – ta)) γ

Δx'' = ((8,3-0) + 0,8 (2 -0))/0,6

Δx'' = ((8,3 + 0,8 (2))/0,6 = 16,5 minuti luce

Giusto per conferma nella figura l'intervallo di tempo Δt’' corrisponde a un intervallo misurato sull'asse del tempo t di 24 minuti (22 + 2 = 24).

Visto dal sistema di riferimento del terricolo, il tempo dell'astronave appare dilatato, ossia:

Δt'' = Δt 1/γ = 24 x 0,6 = 14,4 minuti

Inoltre per il sistema del terricolo (x=27,5) , anche lo spazio dell'astronave appare contratto:

Δx'' = Δx 1/γ = 27,5 x 0,6 = 16,5 minuti luce.

Anche in questo caso i risultati coincidono.

Inoltre la distanza spaziotemporale tra i due eventi non deve cambiare:

T''²- X''² = 14,4² - 16,5² = -64,89.

Quindi T² – X² = T'²- X'² = T''²- X''² .