Categorie: Fisica classica Matematica Quiz
Tags: Achille cicloide quiz tartaruga
Scritto da: Club dei Maghi
Commenti:24
Quiz: La "rivincita" di Achille
La rabbia, l'orgoglio e la forza della ragione
Dopo avere in parte sfogato l'ira funesta prendendo a calci lo slittino, Achille si mise a riflettere sui fatti della giornata.
La Tartaruga si era tolta una soddisfazione colossale: lo aveva acchiappato sul traguardo ogni volta, anche quando era partito con un vantaggio enorme, a pochi centimeti dall'arrivo.
Aveva bisogno di una rivincita immediata. Se solo avesse potuto parlare con il suo allenatore Zenone, per farsi consigliare...
Guardando il panorama mentre il Sole stava tramontando, si accorse di una cosa che non aveva notato prima. A lato della maledetta pista su cui avevano gareggiato, partendo dalla stessa altitudine e scendendo con pendenza costante fino al traguardo, si stendeva una pista parallela perfettamente lineare.
Questa scoperta gli fece balenare l'dea di una nuova sfida con il tardigrado (Achille non sapeva che il tardigrado è anche un curioso, minuscolo “animaletto”, chiamato orso d'acqua, che è in grado di entrare in uno stato di disidratazione e sopravvivere in ambienti estremi, tra cui il vuoto siderale. Era convinto, il Pelide, che fosse solo una forma un po' dispregiativa riferita al lento incedere della tartaruga)
Va bene, volete vedere il tardigrado, eccolo...
Bene, adesso che l'avete visto, andiamo avanti.
Dunque, Achille pensava “Se io mi piazzo sulla sommità della discesa in pendio costante e la tartaruga parte dalla stessa altezza sulla “sua” maledetta pista arcuata, io mi muoverò in linea retta, dritto dritto fino al traguardo, mentre lei dovrà seguire la curva della pista che, ovviamente sappiamo essere più lunga. Mi ricordo benissimo che qualcuno ha dimostrato, non so in quale occasione, che la minima distanza euclidea tra due punti (già, che fosse Euclide? O forse Pitagora? Boh?) è quella del segmento di retta che li congiunge.
Ecco cosa faremo! E vincerò sempre io, senza fare nessuna fatica. Sì, arriverò di certo prima di lei.
Più tardi a cena, proprio mentre era sul punto di lanciare la sua sfida per il giorno dopo, la tartaruga si lanciò in una interminabile e noiosissima dissertazione sulla cicloide, così si chiamava il profilo della pista.
“Sai Achille, quella curva è proprio speciale. Pensa che la sua area è esattamente il triplo dell'area del cerchio che la genera, la sua proiezione sull'asse orizzontale, ovviamente, è pari allo sviluppo della circonferenza, cioè 2πR, e il periodo della oscillazione, come ormai sai, indipendente dal tempo, vale T = 2π √ 4R/g.”
A quest'ultima affermazione Achille drizzò le orecchie. Quindi se quello era il tempo del periodo completo, il tempo di discesa doveva esserne la quarta parte. Cioè Td = π√ R/g. E proprio quello era il tempo da battere. Una informazione su cui ragionare, facendo le opportune verifiche. Chissà di quanto sarebbe stato sotto quel tempo. La sfida avrebbe potuto lanciarla benissimo la mattina seguente.
Ritiratosi nella sua camera, Achille si mise a fare un po' di conti. All'università di Ftio, dove suo padre Peleo lo aveva iscritto a viva forza, se l'era cavata per il rotto dell'elmo in tutte le materie. Non l'avevano cacciato, anzi gli avevano pure conferito la laurea, solo perché, oltre a essere il figlio del Re era il capitano della squadra di atletica.
Però non era uno stupido e qualche idea gli era rimasta in testa. Mettendo insieme quello che ricordava e consultando Wikipedia (voi potete farne a meno) arrivò alla stravolgente conclusione che non avrebbe affatto vinto con il suo sistema della pista in piano inclinato, anzi, sarebbe arrivato con un distacco notevole sulla Tartaruga. Meno male che aveva fatto i suoi conti.
Così, sbollita la rabbia e messo da parte l'orgoglio, Achille si risolse di ascoltare la ragione e della sua auspicata ma illusoria rivincita non ne fece più nulla.
In base a quali calcoli Achille è giunto a questa conclusione?
La tartaruga avrebbe accettato la scommessa?
Come sarebbero andate le cose il giorno seguente se si fosse svolta la gara immaginata da Achille?
QUI la soluzione
QUI tutti i quiz del blog
QUI altri percorsi da calcolare!
24 commenti
Chiedo perdono ai maghi... ma mi permetto di inserire un quiz nel quiz, ossia un quiz2
La cicloide è una curva fantastica e tornerà a farsi viva nel Circolo... Mentre cercate di risolvere questo simpatico e istruttivo quiz, potreste anche pensare a come usare la cicloide per disegnare, abbastanza facilmente, un quadrato che abbia la stessa area del cerchio di partenza. Ebbene sì... con la cicloide si può quadrare un cerchio (ma non bastano riga e compasso...
).
Naturalmente, amici, non è detto che si debba trovare subito un quadrato. Il quadrato è una cosa con ben 4 lati. Magari è più facile trovare prima un triangolo che ha solo 3 lati ...( si potrà dire "triangolare un cerchio " ? )
non voglio importunare oltre... ma si può anche arrivare subito a un quadrato! Ah ... la cicloide... che curva neravigliosa...
Io credo che abbiamo in mente la stessa costruzione.... Comunque lasciamo fare ai volenterosi volontari.
Se non ho male interpretato, in estrema sintesi bisogna dimostrare che, a parità di condizioni e ipotesi (il moto avviene senza dissipazione di energia: non ci sono attriti nei punti di contatto con la pista, l'impatto dell'aria non è da considerare (come se il moto avvenisse nel vuoto), i concorrenti vanno considerati come corpi rigidi (privi di movimenti interni, non possono neppure tossire) , non c'è alcun rotolamento ma solo scivolamento (strisciamento senza attrito), il tempo necessario per arrivare partendo dal punto più alto rispetto al piano di terra, deve essere sempre minore per chi scorre sulla semicicloide sino al traguardo, che sul segmento racchiuso tra questi due punti.
Meglio le immagini:
Allego anche immagine animata che mostra il tempo impiegato da punti che scorrono su diverse curve per transitare dallo stesso traguardo:
https://imgur.com/qTs2tkz
Che dire, Andy, sei stato velocissimo e hai colto con precisione millimetrica il bersaglio. Ottima l'animazione che mostra bene quale disastroso ritardo avrebbe accumulato il povero Achille se avesse gareggiato in quelle condizioni. (come nei telefilm del tenente Colombo sappiamo già tutto sul "cosa" ma si tratta di capire il "come" e il "perché" .)
Ti chiedo solo un piccolo ulteriore passaggio per quantificare il rapporto tra il tempo del secondo arrivato e quello del vincitore, come avrai già osservato, i maghi sono un po' pedanti...
Dopo di che... potrai dedicarti fruttuosamente a quadrare il cerchio generatore della cicloide, cogliendo l'invito di Vincenzo.
Per chi intendesse portare a termine la propria soluzione, suggerisco di non aprire i link inseriti nel commento di Andy, ma di proseguire per la propria strada e di presentare il risultato in un commento.
In questo senso è un ottima strategia anti-spoiler quella seguita dall'amico Andy, che lascia avvolto in un alone di privacy il metodo seguito e i risultati ottenuti.
Al lavoro !
le soluzioni, sempre precise, che fanno uso di carta e matita di Andy stanno ormai diventando "mitiche"!
Che non sia l'unico uomo capace di quadrare il cerchio con riga e compasso?
Complimenti!!!
Ecco il rapporto tra i due tempi di percorrenza:
https://i.imgur.com/dbnbNtq.jpg
Piccola osservazione personale: tale rapporto è indipendente dalla misura del raggio della circonferenza generatrice e dal valore di g, per cui, premesse le ipotesi iniziali e a parità di condizioni, se l'esperimento si potesse condurre sulla Luna, su Marte, su Giove, sul Sole, sulla superficie di qualunque oggetto che eserciti attrazione gravitazionale di valore finito, il valore adimensionale del rapporto rimarrebbe costante.
I buchi neri sono esclusi
Perfetto, Andy, adesso non hai alternative.... devi pensare alla quadratura del cerchio mediante la cicloide !
Ultimamente sta diventando più difficile far quadrare i propri conti con non la quadratura del cerchio.
Comunque, ecco che mi è venuto in mente (con il supporto della cicloide):
https://i.imgur.com/4zlEWlK.jpg
Va bene Andy...anche questa è fatta. Ora, che possiamo proporti per non tenerti in ozio?
Non so...vuoi riflettere su cosa sarebbe successo nelle due gare tra Achille e la tartaruga se, invece di porre l'ipotesi che la accelerazione g sia costante e indipendente dalla posizione, avessimo ipotizzato che g varia in funzione della altitudine ( in realtà questa dipendenza esiste, anche se generalmente non se ne tiene conto). Diciamo che non è il caso di fare calcoli, ma solo di ragionare qualitativamente sulla influenza che avrebbe potuto avere questa ipotesi sulle prestazioni dei concorrenti nelle due gare.
Caro Maurizio,
se ho ben inteso, si può ipotizzare che il valore di g vari man mano che i due corpi scivolano sulle rispettive curve (per la precisione dovrebbe aumentare via via che si scende di quota, in quanto diminuisce la distanza dei due corpi con il centro di massa dell’oggetto che esercita attrazione gravitazionale e sul quale si svolge la competizione).
Ora, sia dalla geometria delle due curve, che dalle simulazioni animate, si nota che il corpo che scivola sulla cicloide è costantemente più vicino al piano di terra (e di conseguenza al centro di massa) rispetto a quello che scivola sul piano inclinato (i due corpi si trovano alla stessa quota solo in 2 punti: alla partenza e all’arrivo), quindi il corpo che scivola sulla cicloide anticipa l’aumento di attrazione gravitazionale rispetto a quello che scivola sul piano inclinato aumentando ancora di più la sua velocità relativa rispetto al percorso compiuto;
in parole povere, il distacco temporale tra i due dovrebbe aumentare a vantaggio del “cicloideo”.
Caro Andy, è quello che penso anche io, il vantaggio aumenta il vantaggio.
Vedo che fai riferimento alla gara di rivincita, in cui un concorrente (Achille) scende sul piano inclinato, mentre l'altro (la tartaruga) scende lungo la cicloide.
Per quanto riguarda la prima gara ambedue utilizzano la stessa pista a cicloide, ma non partono dal mededimo punto. Come andranno le cose nella nuova ipotesi?
Il problema è più complesso di quanto sembri; ipotizzando un g crescente in funzione dell’altezza (decrescente) del punto materiale rispetto al piano di terra, h non decresce in maniera costante, ma segue il particolare profilo della cicloide, cioè per ogni Δs variabile in orizzontale, corrisponde un Δs variabile in verticale e il rapporto tra le due variabilità non è costante.
Si potrebbe calcolare una sorta di tempo medio (per comodità si può imporre il raggio del cerchio generatore pari ad 1 unità di misura), per esempio chi parte dal punto a quota massima (h = 2 unità):
Tm = (1/n)π[sqrt((g1)^-1) + sqrt((g2)^-1) + sqrt((g3)^-1) + … + sqrt((gn)^-1)]
con g1 < g2 < g3 <….< gn.
Discorso analogo per chi parte da più in basso, solo che il suo g iniziale parte da un valore maggiore rispetto al g iniziale (g1) del punto che parte da quota massima, ma nel calcolo del tempo medio computa meno g da portare in sommatoria.
Effettivamente, nella realtà, g decresce perché calcolando il valore di g come:
g = GM / (R +h)^2, g si può considerare costante sino a quando il rapporto h / R è molto piccolo.
Che ti posso dire, anche con un g via via crescente, ad intuito, i 2 periodi di tempo per completare la discesa dovrebbero continuare ad equivalersi.
Rileggendo il testo del quiz...
La tartaruga ha detto chiaramente ad Achille che, sulla stessa pista a cicloide, il periodo di oscillazione del moto armonico è uguale per tutti, indipendentemente dal punto di partenza. Questo fatto ha determinato l'arrivo sincronizzato al traguardo, nella gara in cui abbiamo posto g=costante.
Ha anche detto quale legame intercorre tra il tempo di oscillazione, le dimensioni lineari della pista e la "costante" di gravitazione g.
Se la gara sulla cicloide si fosse svolta in contemporanea, uguali piste in due luoghi diversi, ad esempio, con Achille sulla Terra e la tartaruga sulla Luna, essendo i valori di g diversi ....
Se la gara sulla cicloide si fosse svolta in contemporanea, uguali piste in due luoghi diversi, ad esempio, con Achille sulla Terra e la tartaruga sulla Luna, essendo i valori di g diversi ....
Essendo Td = π√ R/g il periodo di tempo necessario per coprire il percorso cicloideo da quota massima sino al punto di minimo assoluto della cicloide, e dato che g della Luna è minore di g della Terra, quello sulla Terra impiega sempre un tempo minore a coprire il percorso su metà cicloide rispetto a quello sulla Luna.
Anche se era stato chiesto: "cosa sarebbe successo nelle due gare tra Achille e la tartaruga se, invece di porre l'ipotesi che la accelerazione g sia costante e indipendente dalla posizione, avessimo ipotizzato che g varia in funzione della altitudine"
Precisamente... se la g è maggiore il periodo è minore. Insomma Achille (sulla Terra) sarebbe arrivato al traguardo prima della Tartaruga (sulla Luna).
Ora, venendo alla domanda che richiami in chiusura, potremmo dire che ad ogni istante il periodo di chi sta più in basso è minore del periodo di chi sta più in alto (visto che la g è maggiore in basso).
La g a cui è soggetto Achille, almeno in partenza è maggiore di quella della Tartaruga, e le due "g" diventeranno uguali solo quando i due contendenti si troveranno affiancati... Ma se, nelle condizioni a g costante per tutti, questo affiancamento si realizza solo all'ultimissimo istante, allora...
Alla fine non ho scritto più niente perché Andy è stato molto esaustivo. Penso che l obiettivo nascosto del quiz fosse il fatto che la cicloide è una curva brachistocrona,ovvero quella che che collega due punti nel minor tempo possibile. Questo fatto è noto in letteratura anche se la dimostrazione non è immediata. In pratica come nelle animazioni di Andy su di essa il tempo di percorrenza è il minore. Sempre guardando l animazione di Andy mi era venuto in mente che si potrebbe provare a fare i calcoli per la parabola. Ciò comporta però di saper esprimere l elemento infinitesimo ds della curva , dividerlo PER la velocità istantanea e integrarlo sugli estremi. NON HO PERÒ PROVATO a farlo. Potrebbe essere una idea..
Certamente l'argomento è ricco di sviluppi e con il solo intuito non si può andare oltre un certo punto. Riprenderemo in futuro questi argomenti, parlando ancora della cicloide e delle sue molteplici proprietà, talvolta davvero sorprendenti e confrontando la dinamica che introduce , come suggerisce Umberto, comparandola con quella tipica di altre curve.
Lascerei ancora uno o due giorni per coloro che volessero aggiungere qualche altra considerazione, poi il Club dei Maghi fornirà la soluzione, peraltro già svelata dall'amico Andy.
se aspetti fino a domani sto facendo dei conti alternativi a quelli di Andy. Così tanto per variare.
Ok Umberto, fai pure con calma...
Quello che volevo far notare nel precedente commento, è che è possibile una soluzione alternativa , e generalizzante.
Sappiamo infatti dal calcolo differenziale, che l'elemento infinitesimo di lunghezza di una curva in una variabile, y(x),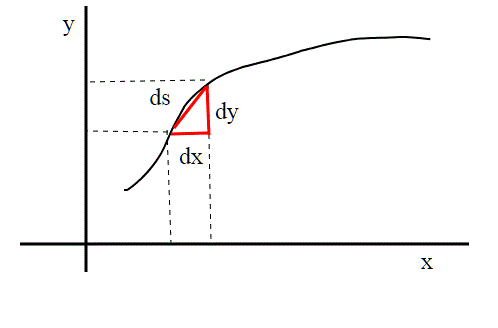
il ds, si può ricavare da:
raccogliendo si ottienedx^{2})
.
per l'uguaglianza fra energia potenziale e cinetica, la velocità istantanea è data invece da:
v=)})
(vo iniziale =0)
ma allora il tempo infinitesimo, dt, è dato dal rapporto ds/v, ovvero}}{\sqrt{2gy}}\cdot&space;dx)
il tempo totale, qualsiasi sia y(x), sarà allora
Nel nostro caso, ovvero con i dati del quiz,
sempre nel caso che la velocità iniziale sia V0=0.
Sempre nel caso particolare del quiz,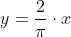
, che è la retta del piano inclinato.
e l'integrale diventa:
l'integrale indefinito viene:
e calcolato l'integrale definito fra [0,
R]
e svolgendo i calcoli:
Di sicuro questo non è il metodo più naturale nel caso del piano inclinato, ma l'ho introdotto per generalizzare il discorso; esso si può applicare per trovare il tempo di arrivo indipendentemente dalla curva, cioè y=f(x) può essere una qualsiasi curva che unisce i due punti. Di sicuro l'integrale 1) non sempre è facilmente risolvibile come in questo caso. Bisognerebbe provare con la parabola e il cerchio.
Per risolvere ancora in modo più generico il problema, bisognerebbe cercare la funzione che rende minimo l'integrale 1). E qui potremmo applicare quello che tanto ha fatto faticare Fabrizio, ovvero le equazioni di Eulero-Lagrange, che ci porterebbero ad una equazione in cui l'incognita è una curva (equazione differenziale).Io non mi cimento, ma qualcuno lo farà. In tal caso scopriremmo proprio,come è noto dalla letteratura matematica, che tale curva è proprio una cicloide.
Mi chiedevo quale potesse essere la velocità nel momento del taglio del traguardo sia per chi scorre sul piano inclinato che per chi scorre sulla semicicloide (il punto del traguardo è comune alle due curve):
La semicicloide misura 4R di lunghezza, la linea di piano inclinato misura R*[(4 + π^2)^(1/2)] di lunghezza,
4R / R*[(4 + π^2)^(1/2)] = 4 / [(4 + π^2)^(1/2)] = 1,074... > 1
per cui, il punto sulla semicloide che impiega meno tempo per percorre un tragitto più lungo per arrivare al traguardo rispetto al punto che scorre sul piano inclinato, deve possedere una velocità media superiore:
https://i.imgur.com/75i65do.jpg
Spero di non aver sbagliato impostazioni e/o calcoli
Caro Andy, siamo sul punto di pubblicare la soluzione. Troverai pane per i tuoi affilati canini....