Precisazioni sulla soluzione del quiz "Polinomi e derivate"
Pur avendo promesso di non scrivere la soluzione di questo quiz, è necessario che dia delle precisazioni su un punto importante,anzi essenziale, della dimostrazione. Mi affido al primo commento di Fabrizio:
"La derivata h-esima di uno dei termini del polinomio è:".
Sostanzialmente, per risolvere il quiz, basta dimostrare che è divisibile per h!
A questo punto succede quello che succede spesso in matematica; ci si accorge che quel numero rappresenta qualcosa in altro ambito. Chi ha studiato il calcolo combinatorio, si accorge subito che il numero altro non è che il numero di disposizioni Dn,h. Le righe di spiegazione che seguono presuppongono che alcuni concetti siano già noti a lettore. Cominciamo con la regola fondamentale del calcolo combinatorio:
Regola fondamentale del calcolo combinatorio:
Se un oggetto è costruito con una sequenza di h scelte e vi sono n1 possibilità per la prima scelta, n2 per la seconda, …, nh per la h-esima, il numero totale degli oggetti così ottenibili (h-uple ordinate) è n1⋅n2⋅…⋅nh. Questa regola si può dimostrare formalmente usando il prodotto cartesiano di insiemi e il principio di induzione.
Disposizioni di n oggetti a h alla volta
Se Ω è un insieme che ha n elementi, per disposizione degli n oggetti di Ω a h alla volta, 1≤h≤n, intendiamo una h-upla ordinata costruita con h elementi distinti di Ω.
Per la regola fondamentale del calcolo combinatorio il numero delle disposizioni di n oggetti a k alla volta è allora:
( Dn,k = n⋅(n-1) ⋅…⋅ (n-h+1) poiché la prima scelta può essere fatta in n modi, la seconda in n-1 modi
(perché deve essere diversa dalla prima),…, la h-esima in n-h+1 modi.
Esempio: il numero di parole di h lettere distinte che si possono costruire con un alfabeto di n≥h lettere (beninteso qui col termine “parola” intendiamo una h-upla ordinata di lettere che può anche non avere alcun senso).
Un altro oggetto molto importante del calcolo combinatorio, è rappresentato da:
Coefficienti binomiali
Una combinazione di n oggetti a h alla volta, h≤n, è un sottoinsieme,di cardinalità h, dell’insieme Ω che ha gli n oggetti come elementi.
Il numero delle combinazioni di n oggetti a h alla volta, 1≤h≤n , è indicato con Cn,h oppure anche con . Chiaramente nessuno può dubitare che questo numero non sia un intero. Alle differenza delle disposizioni, dove conta anche l'ordine, nelle combinazioni contano solo gli oggetti scelti.
Esempio: se abbiamo un insieme di n elementi e cerchiamo il numero di sottoinsiemi di 2 elementi, chiaramente i due sottoinsiemi {a,b},{b,a} sono lo stesso insieme,quindi viene contato solo una volta.
Che relazione c'è fra Dn,he Cn,h? Se indichiamo con Cn,h= x il numero naturale cercato, tra x e Dn,h (il numero delle disposizioni di n oggetti a h alla volta) c’è evidentemente la relazione Dn,h = x⋅ (h!) dal momento che una fissata combinazione di h oggetti dà luogo a h! permutazioni degli stessi, ciascuna delle quali costituisce una diversa disposizione. Bene, senza calcolare Cn,h che in questo contesto non interessa , abbiamo dimostrato che p= Dn,h =n⋅(n-1) ⋅…⋅ (n-h+1)= x⋅ (h!), ossia che p è divisibile per h!. Bene, allora abbiamo finito.
Speravo che qualcuno trovasse una soluzione più diretta, ma se ci pensate bene il calcolo combinatorio non è proprio fuori luogo quando si parla di polinomi o derivate; i coefficienti binomiali si chiamano così perchè entrano nello sviluppo del binomio di Newton, mentre i fattoriali saltano sempre fuori nelle derivate dei polinomi o nelle serie di potenze. Per me questa soluzione basta e avanza; a noi serve per proseguire in un programma affascinante che voglio continuare immediatamente. Se Maurizio o Fabrizio , o tutti e due assieme vogliono scrivere una soluzione alternativa, ben venga!






5 commenti
Nella precisazione sulla soluzione del quiz "polinomi e derivate" , Umberto scrive:
Sostanzialmente, per risolvere il quiz, basta dimostrare che...(n-h+1)) è divisibile per h!
è divisibile per h!
Riscrivo il prodotto p in forma diversa ed equivalente:
Al numeratore appare h! Pertanto occorre e basta dimostrare che è sempre intero il rapporto
Sia al numeratore , sia al denominatore, compaiono (n-h) numeri consecutivi che vengono moltiplicati tra loro. Distinguo, nella sequenza al numeratore, un valore minimo (m) e un valore massimo (M) di questi numeri.
Moltiplicando r per la frazione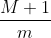 ottengo al numeratore di r una nuova sequenza di numeri consecutivi in cui tutti i valori precedenti risultano incrementati di 1. Avrò quindi nuovi valori di m e di M.
ottengo al numeratore di r una nuova sequenza di numeri consecutivi in cui tutti i valori precedenti risultano incrementati di 1. Avrò quindi nuovi valori di m e di M.
Iterando questo meccanismo posso scrivere qualsiasi sequenza di (n-h) numeri consecutivi al numeratore del rapporto r
La cosa fondamentale da notare è che ogni volta che moltiplico per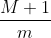 introduco al numeratore un valore che , dopo (n-k) passi, apparirà nel denominatore. Questo fatto garantisce che , essendo partiti da un numero intero, a ciascun passo otterremo un numero intero.
introduco al numeratore un valore che , dopo (n-k) passi, apparirà nel denominatore. Questo fatto garantisce che , essendo partiti da un numero intero, a ciascun passo otterremo un numero intero.
Il rapporto r sarà quindi sempre intero e questo implica che il polinomio p sarà sempre divisibile per h!
ok Maurizio ci penserò sopra. Potevi però scrivere questa soluzione da un altra parte come ti avevo consigliato. Così facendo stai creando confusione ai lettori. Ho messo questa precisazione appunto qui;,cosa centra col tuo commento? Sta forse cercando di invalidarla anche se questo è impossibile?
ottimo ed elegante
Caro Umberto, scusa la involontaria invasione ma non avevo capito che suggerivi di parlarne altrove.
Lontana da me l' intenzione di invalidare quello che hai scritto, dato che valuto la tua soluzione ineccepibile e didatticamente efficace il collegamento con il calcolo combinatorio.
La mia proposta resta un tentativo di descrivere in un modo diverso il cammino verso il medesimo traguardo.
Mi associo all'apprezzamento espresso da Leandro che immagino si riferisca alla esposizione presentata nell'articolo di Umberto
Ti ripeto che è solo la posizione che è sbagliata; o bisognava continuare nel quiz, oppure come avete fatto altre volte scrivere una soluzione alternativa in un nuovo articolo. Intendevo questo nella frase:
"Se Maurizio o Fabrizio , o tutti e due assieme vogliono scrivere una soluzione alternativa, ben venga!"
comunque ormai lasciamolo lì.