QUIZ: Quel pazzo, pazzo, pazzo poligono ***
Ormai sembra proprio che il Prof. Nobody si sia arreso all'intelligenza e prontezza di Peppa, Pappo e Pippo. Tuttavia, ecco che inaspettatamente compare il fratello gemello di Nobody, il Prof. Somebody. Accidenti… lui sembra essere veramente di un altro livello. Questa volta sarà dura per i nostri amici… Cercate di aiutarli!
Nobody sembra ormai essere sparito dalla vita di Pippo, Pappo e Peppa… Tuttavia, ecco comparire davanti ai nostri amici un individuo che sembra una copia perfetta di Nobody, se non fosse per i suoi occhi vispi e furbi e l’ampio sorriso benevolo. Si presenta subito come il gemello “buono” di Nobody, interessato soltanto a trovare persone di grande logica e capacità riflessive.
“Mio fratello ha parlato molto di voi ed è furente per non essere mai riuscito a prendervi “in castagna”. A tal punto che mi sono convinto che voi siete gli unici a poter competere con me nella soluzione di problemi di tipo geometrico, matematico e fisico. Non potevo non approfittarne e mettervi alla prova. Ovviamente, a me interessa solo sollevare interesse e non minaccio punizioni o ricatti vari. Io sono solo un grande appassionato…”.
Pappo, Peppa e Pippo si convincono dell’onestà e sincerità di Somebody e lo invitano a porgli un problema. Somebody non se lo fa dire due volte e inizia la sua presentazione, composta di 4 disegni, all’apparenza abbastanza semplici: “Il primo disegno vi mostra un esagono regolare inscritto in un cerchio. In rosso è stato tracciato un segmento.
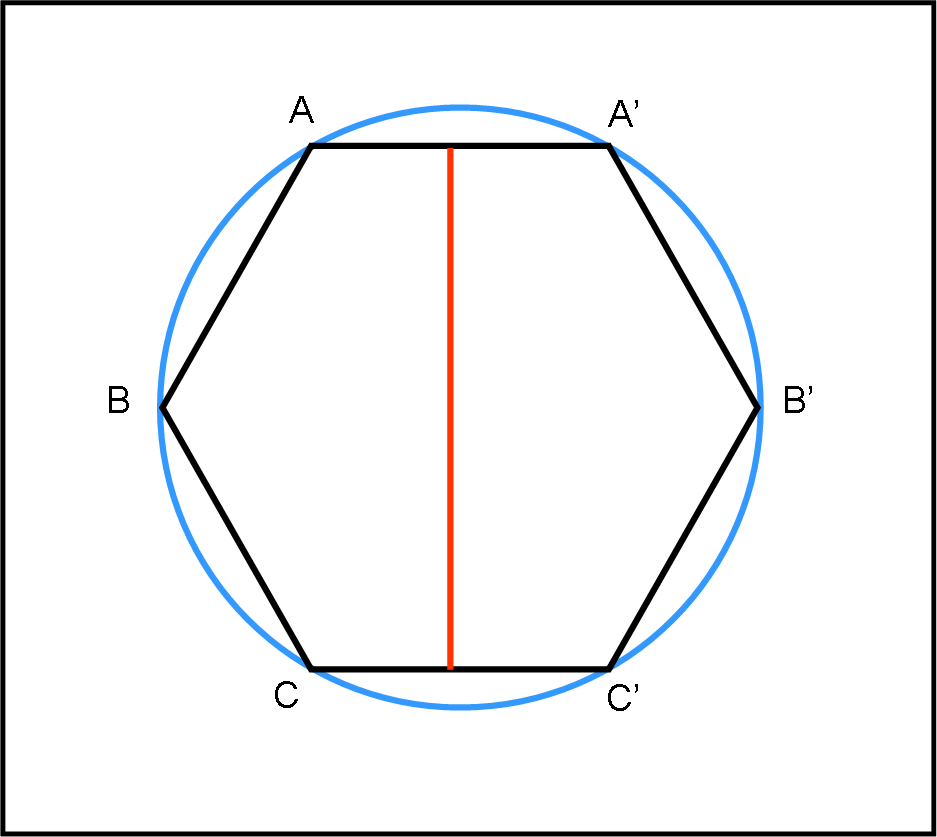
La domanda, che varrà per ogni disegno, è semplicissima: “che legame vi è tra il segmento e l’esagono? O, se preferite, cosa rappresenta il segmento per l’esagono? Il secondo disegno riporta lo stesso cerchio e un altro esagono non più regolare. Anche in questo caso il segmento rosso è strettamente legato all’esagono, con la stessa regola di quello precedente.
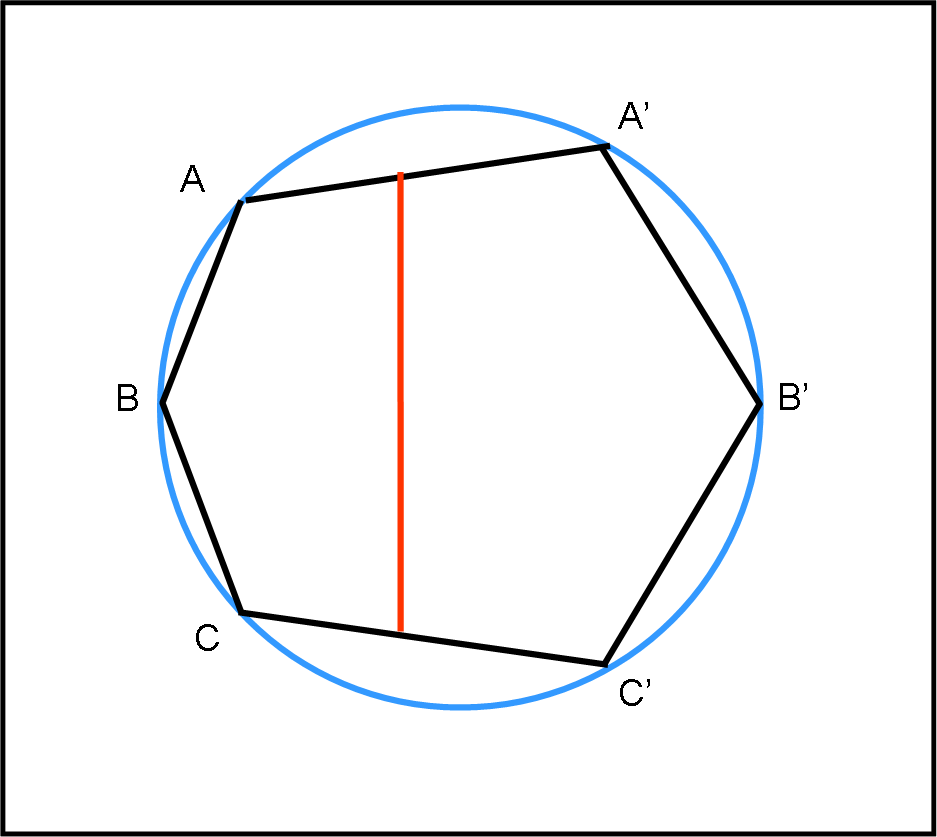
Nel terzo disegno complichiamo un poco le cose, rendendo ancora più “strano” l’esagono… Il segmento compare nuovamente e il suo legame all’esagono è sempre lo stesso dei casi precedenti.
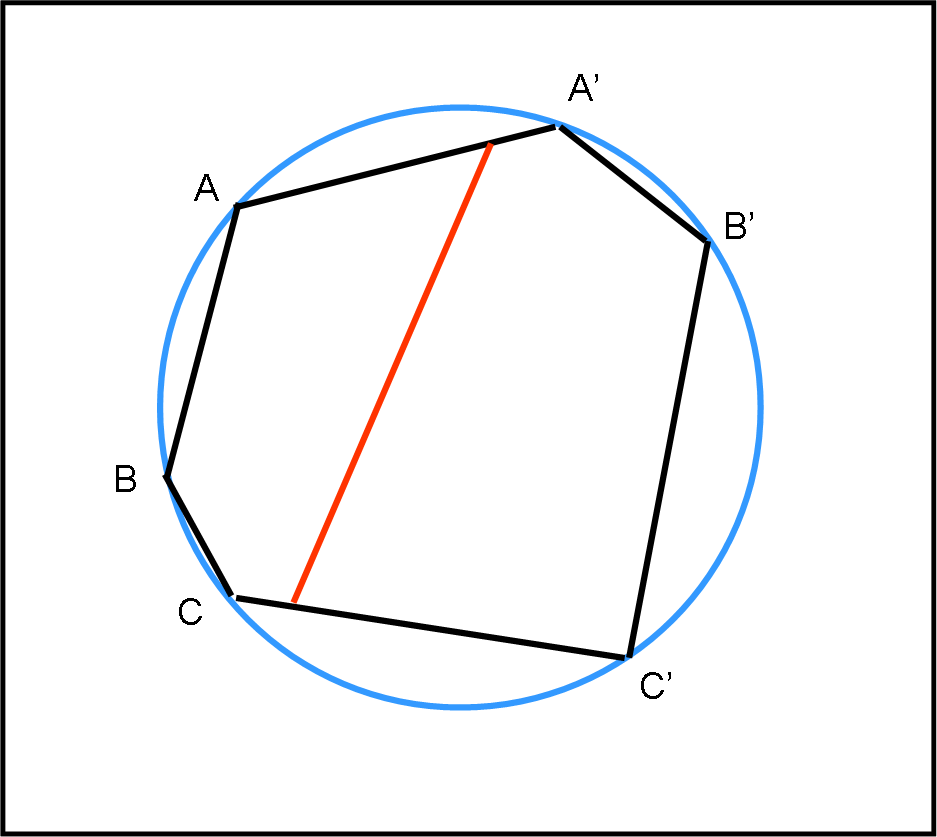
Probabilmente, siete riusciti a capire cosa lega esagono e segmento… (se siete così svegli come dice mio fratello). Vi chiedo allora di considerare l’esagono del quarto disegno e disegnare il segmento corrispondente. Posso solo dirvi che vi ho già aiutato molto…”
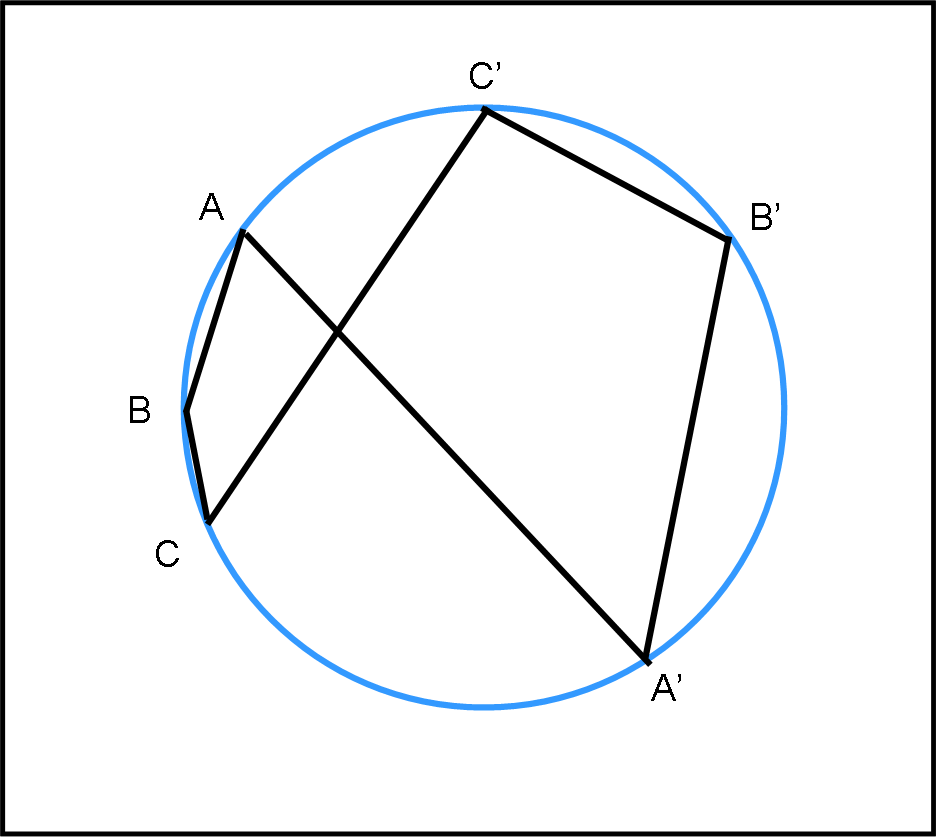
I nostri fratelli rimangono alquanto storditi. Cercano in tutti i modi di trovare il legame che esiste tra i primi tre esagoni e il segmento che li taglia in modo che sembra quasi casuale. Se il primo disegno ha molte possibilità, il secondo ne ha molte meno e il terzo sembra del tutto slegato da una logica qualsiasi. Il quarto esagono, poi, sembra rendere la difficoltà insormontabile…
I nostri fratelli sembrano sul punto di “abbandonare”, ma, finalmente, uno di loro ha l’idea vincente. Il caso è risolto e Somebody si complimenta con loro, spiegandogli come quel problema apparentemente assurdo abbia risvolti importantissimi in geometria.
Forza, maghi, maghetti, apprendisti e lettori silenziosi… è il momento di dire la vostra. Non abbiate paura a sparare qulasiasi cosa vi possa sembrare in tema, anche se un po' "stramba". Ricordiamoci che la Meccanica Quantistica ci ha già dimostrato che l'assurdità può essere la migliore rappresentazione della realtà...
Poi potremo anche inserire il quiz in un discorso più ampio…
QUI la soluzione
20 commenti
Mah, rompiamo il ghiaccio, via
A me l'unica cosa che per ora viene in mente è che il segmento rosso, nelle prime tre figure, collega un punto del lato AA' con un punto del lato CC'. Quindi nella quarta figura il segmento collegherebbe un punto di AA' con uno di CC'. Ma mi sembra troppo poco.
Sono ancora molto lontano ma, per le prime 3 figure, mi sembra che il segmento rosso passi per il punto di incontro di AC'-A'C-B'B, che sia diviso da questo punto in due parti uguali e che i suoi estremi giacciano sui segmenti AA' e CC'; il segmento rosso sembra avere, nei tre casi, lunghezza diversa.
siamo anora molto lontani... anche se Gianni ha detto una cosa utile...
Per onestà, devo dire che quel "mostro" di Pautasso ha già risolto il problema, ma gli ho chiesto di togliere il commento per non influenzare gli altri concorrenti...
Devo dire che, mai come questa volta, i nostri tre amici cadono proprio a fagiolo...
La butto lì, anche se sembra un po strampalata:
la linea rossa, nei primi 3 casi, passa sempre per 3 punti:
il punto di incontro dei segmenti che uniscono BB’, AC’, AC;
il punto di incontro delle diagonali dei trapezi superiore e inferiore che si ottengono unendo B con B’.
Nella prima figura, l'esagono regolare inscritto si può dividere in 6 triangoli equilateri uguali tra loro,
con il lato uguale al raggio del cerchio circoscritto (L = r), per cui la misura del segmento rosso sarà il doppio dell’altezza di un singolo triangolo equilatero:
2 * L * sen(60) = 2 * L * (1 / 2) * √3 = L * √3
ora, rapportando la misura lineare del segmento rosso con il perimetro dell’esagono, pari a 6L:
(L * √3) / 6L = (1 / 6) √3.
La figura 2 sembra la 1 leggermente ruotata secondo l’asse su cui giace la linea rossa e in senso orario, rispetto alla 1; ora se il legame è sempre lo stesso, anche qui il rapporto lunghezza linea rossa / perimetro esagono = (1 / 6) √3.
La figura 3 sembra leggermente ruotata come prima, ma anche inclinata verso “dietro” rispetto ad un osservatore frontale; stesso discorso dei due casi precedenti, il rapporto lunghezza linea rossa / perimetro esagono = (1 / 6) √3.
La figura 4 oltre ad essere ruotata e inclinata, sembra abbia subito una torsione di 180°, per cui la linea rossa dovrebbe diventare una spezzata.
caro Andy (e tutti gli altri),
non soffermatevi troppo sulla lunghezza del segmento rosso, ma sulla sua posizione... la lunghezza non ha interesse e non è collegato al problema sollevato...
spero sia di aiuto...
A meno che, per l'ultima figura, dato che nelle figure precedenti oltre che per il punto di incontro dei segmenti che uniscono gli angoli contrapposti, la linea rossa passa per i punti dati dall'incrocio:
AB' -> A'B
BC' -> B'C
questi punti si collocano fuori dall'esagono e anche dal cerchio, rappresentando gli estremi del segmento rosso.
In riferimento al mio commento precedente:
https://i.imgur.com/Z56IgyP.png
fuochino, fuochino....
Update dell'immagine precedente, con aggiunta dei collegamenti AC' e A'C
https://i.imgur.com/X0YIxoT.png
Ultima immagine e poi mi ritiro a vita privata
https://i.imgur.com/UygdSQK.png
Sono nella fase (forse) di maggior allontanamento:
il centro del segmento non può essere (se non in casi particolari) l'intersezione delle tre rette che congiungono i vertici degli angoli contrapposti
il centro del segmento potrebbe essere l'intersezione di due rette (magari una passante per AA' ed una per CC') ed il segmento potrebbe essere perpendicolare al segmento BB' e delimitato dalle sue intersezioni con AA' e CC': spiega la figura 1 e la 2, ma non la 3
potrebbe esserci una relazione con il fatto che, sia nella figura 1 che nella 2, BB' sembra essere orizzontale, mentre nella figura 3 BB' forma un angolo con l'orizzontale (...?)
ho (tra i tanti) un dubbio: la figura 3 rappresenta due quadrilateri (e quindi l'esagono in esame si ottiene congiungendo, in sequenza A, C', B', A', C e B) o è definibile "esagono" anche una figura in cui due lati si intersecano?
Viene direttamente dal teorema di Pascal (prima che battesse la testa).
Eh sì... dice bene Leandro e disegna bene anche Andy.
In realtà, io avevo scritto che uno solo dei fratelli dà la risposta. Indovinate chi è?
Quella di Pascal è una specie di generalizzazione alle comiche...
Ho l'impressione che Andy abbia fatto centro: segmento allineato sui tre punti e delimitato dalle intersezioni dei prolungamenti di AA' e CC'. Giusto?
Scusate il disallineamento temporale: vedo i vostri messaggi precedenti solo ... dopo aver inviato i miei.
incredibile, non vi si può lasciare soli un attimo...
https://www.youtube.com/watch?v=NIW3-FSzoSY
Ha ragione il Prof. , del resto è più anziano di Pascal.
Eh sì è il più vecchio dei tre fratelli... (qualche secolo soltanto), bravo Leandro!
caro Arturo, in questo circolo, ormai, non basta più la bravura... ci vuole anche la velocità!!!!
Un ultima, personale considerazione...
https://i.imgur.com/lbcwQwt.png
cari amici,
vista la vostra abilità sia teorica che pratica, la prossima volta vi proporrò un problema quasi puramente "meccanico". Torneremo indietro di secoli... e cominciate a preparare gli attrezzi...
Lo sto preparando con calma, perchè non vorrei sbagliare qualcosa... e poi chi vi ferma?!
Sicuramente Artù si sta già leccando i baffi!!!!