Mini Quiz: Uno strano polinomio.
Continuiamo il nostro percorso su derivate e polinomi, di cui ancora non si capisce tanto il senso, ma che porterà però ad una bella sorpresa. Continuiamo a giocherellare con esponenti e derivate, in fin dei conti la teoria dei numeri è molto articolata, perché ha bisogno di vari argomenti della matematica . Fate poi conto che questa è roba abbastanza moderna; si parla del 1949. Questo mini quiz è articolato in più risposte. Potete scegliere quelle che volete.
Consideriamo il polinomio di grado 2n:
, n>0
ove a e b sono numeri interi diversi da zero.
Vogliamo dimostrare alcune "strane" proprietà di questo polinomio.
i) Se indichiamo con la derivata h-esima di f(x), è vero che qualsiasi sia h ,
, ovvero
è un numero intero ?
(suggerimento: tenere presente il risultato del quiz precedente.)
ii) E' vero che ?
iii) supponendo vero il punto ii), riusciamo a dimostrare che ?
Il quiz è aperto a tutti, e anche i più esperti possono partecipare anche subito, se lo ritengono opportuno.
Magari potranno concentrarsi sui punti più difficili, ad esempio risolvendo iii) senza risolvere prima ii) .
25 commenti
scusate, ma non ho resistito a provare il nuovo angolo dei quiz.. il lettori avranno poi la possibilità di cimentarsi su due diversi argomenti, quali geometria e algebra..
hai fatto benissimo Umberto. Con questo angolo attivo, non abbiamo problemi di intasamento della homepage e possiamo inserire tutti i quiz che vogliamo... saranno poi i lettori a scegliere quello che preferiscono. Penso proprio che sia stata un'ottima idea!!!!
bene!
i) consideriamo il membro di destra^{n})
. Essendo una forma binomiale sarà un polinomio costituito da tanti termini di grado da 0 a n i cui coefficienti sono appunto, coefficienti binomiali.
Moltiplichiamo il ternime di sinistra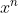
. Questa operazione alzerà i gradi di tutti i termini del valore n.
Otterremo un altro polinomio di grado 2n con termini da n a 2n.
Iniziamo a derivare. Ogni derivazione abbasserà il grado del polinomio di 1 unità.
Consideriemo il termine di grado più basso (cioè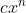
, ove c è il corrispondente coefficiente binomiale) .
Esso diventerà
. Poiché il polinomio non ha termine costante , il valore della sue derivata sarà zero ( che appartiene a Z).
Le derivate successive continueranno a diminuire di 1 unità tale termine e il polinomio varrà sempre zero.
Quando l'ordine h della derivata raggiungerà il valore n tale termine sarà di grado zero, cioè costante.
Questo valore è proprio quello che assume il polinomio per x=0.
Il coefficiente, virtù delle derivazioni applicate n volte assumerà il valore:
Guarda caso l'equazione data ha un divisore proprio uguale a n! che elide il termine fattoriale a numeratore.
Abbiamo però già stabilito che c apprtiene a Z quindi la derivata di ordine n è nulla in zero.
Tutte le derivate di ordine superiore si comporteranno analogamente.
Grazie Leandro, come al solito non posso dire niente. Però non so se tutti conoscano i coefficienti binomiali e il binomio di Newton. Bisognerebbe esplicitare il discorso. Comunque aspettiamo anche gli altri.
come dicevo nel testo ognuno può scegliere la parte che preferisce..non è obbligato a risolvere il tutto. Ma il punto ii) si è alla portata di tutti, é un fatto puramente algebrico..
Rispondo al domanda I.
Scrivo la funzione com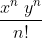e
dove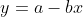 
.
La derivata di un prodotto del tipo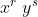
è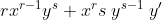 
y' è la derivata di y rispetto ad x che in questo caso è -b.
Quindi ad ogni derivata appaiono addendi con l'esponente ridotto di 1 in uno dei due termini.
Dopo h derivate gli addendi saranno del tipo})
. La riduzione totale dei due esponenti deve essere h.
Poiché cerchiamo il valore della derivata per x=0, molti di questi addendi saranno nulli.
L'eccezione di quello dove non appare più x, cioè dove l'esponente di x è ridotto a 0.
Dobbiamo dimostrare che questo addendo con il suo coefficiente è intero.
Ci sono 5 fattori che compongono questo valore:
Quindi il valore di)
è un intero.
Ben arrivato Fabrizio.. poi ne parliamo
Mi fa piacere che si stiano usando delle vie alternative, tenete però presente che il punto i) si semplifica di molto se si tiene presente il risultato dell ultimo quiz.
Effettivamente il suggerimento di Umberto di utilizzare il risultato del quiz precedente semplifica la dimostrazione.
Per derivate con h<n, tutti gli addendi della derivata contengono x. Quello a potenza minore è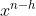
.
Quindi la derivata ha valore 0 per x=0.
Per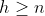
nella derivata c'è un termine costante. Per x=0 questo termine costante è proprio il valore della derivata. Quindi dobbiamo dimostrare che questa costante sia intera.
Utilizzo il risultato del quiz precedente: tutti i coefficienti della derivata h-esima di un polinomio a coefficienti interi sono divisibili per h!.
Il polinomio di questo quiz è un polinomio a coefficienti interi diviso per la costante n!. Quindi i coefficienti della sua derivata possono essere rappresentati da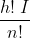
, dove I è un intero. Poiché 
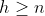, allora anche 
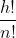è intero. Quindi anche l'addendo costante della derivata h-esima è intero. Ne segue che il valore della derivata per x=0,)
, che è uguale proprio a questo termine constante, è intero.
é proprio così.
La soluzione più diretta della III domanda credo che parta dal risultato della seconda.
Qui utilizzo una via alternativa, visto che sopra sono arrivato alla espressione di uno dei termini che ci interessa .
Con le argomentazione della mia prima risposta si può ottenere che la derivata h-esima calcolata in x=0 è:=\begin{pmatrix}&space;h\\&space;n&space;\end{pmatrix}&space;\frac{h!}{(2n-h)!}\;(-b)^{h-n}\;a^{2n-h})
per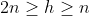 
; 
per gli altri valori di h
Nella risposta precedente non avevo indicato il limiti di validità della espressione.
Dobbiamo confrontare questa espressione con quella della derivata h-esima calcolata per x=a/b,)
. Questo particolare valore è quello che annulla (a-bx) che sopra ho chiamato y.
Anche per questo valore di x, la derivata ha un solo termine diverso da 0 per h nell'intervallo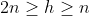
.
Questo termine è quello con}\;y^{n-n})
.
Anche il valore di questo termine è composto da 5 fattori:
Quindi=\begin{pmatrix}&space;h\\&space;n&space;\end{pmatrix}&space;\frac{h!}{(2n-h)!}\;(-1)^n\;b^{h-n}\;a^{2n-h})
E' uguale a=\begin{pmatrix}&space;h\\&space;n&space;\end{pmatrix}&space;\frac{h!}{(2n-h)!}\;(-b)^{h-n}\;a^{2n-h})
a meno dell'esponente di -1.
Si evidenza meglio facendo il rapporto tra le due espressioni che permette di eliminare i fattori uguali:
le risposte alternative vanno sempre bene.. Aspettiamo altri sviluppi
Stiamo parlando di una funzione continua e infinitamente differenziabile.
La f(x) in a/b è nulla e così anche la sua derivata perché deve essere simmetrica in un intorno di a/b.
Segue che la simmetria si estende all'intervallo [0,a/b] .
Inoltre f(x+a/b ) = f(-x) ,
quindi la funzione f (x) è simmetrica, cioè pari, se la consideriamo traslata e centrata in 1/2 a/b
Dall'analisi sappiamo che la derivata di una funzione pari è dispari cioè f(x)=f(-x)
(graficamente è antisimmetrica rispetto al centro di simmetria).
Segue immediatamente che la derivata prima di f(x) in un intorno dello zero avrà lo stesso
valore assoluto e segno della derivata di f(x) per x= a/b.
Passando alla derivata seconda, otteniamo una funzione pari e simmetrica rispetto a 1/2 a/b
quindi il suo valore assoluto in x=0 sarà identico a quello in a/b ma di segno invertito.
Tutte le derivate di ordine superiore avranno lo stesso andamento pari-dispari e quindi con segno
altalenante positivo e negativo.
Ok Leandro, poi tiriamo le somme.
Mi piacerebbe se qualcuno dimostrasse la:
ii) E' vero che=f(\frac{a}{b}-x))
?
Non riesco a capire se sia ritenuta banale
Io direi proprio di sì...
basta sostituire alla x la nuova variabile uguale ad (a/b -x) e il risultato è immediato...
Ok, lo faccio io:
caro Umberto,
in realtà avevo già detto come fare... è un passaggio di algebra elementare... basta semplificare dentro la parentesi e il gioco è fatto
scusa forse ancora non ho capito cosa intendevi, se c è un conto più facile ben venga
scusate se ho insistito sul punto ii) ma la soluzione del punto iii) si semplificherebbe notevolmente. Apprezzo molto i ragionamenti di Fabrizio e Leandro, ma c e un modo naturale di risoluzione che fra l altro occupa poche righe.
Forse Umberto si riferisce a qualcosa di questo tipo come risposta al punto 3.
Valorizzato per x=0 e quindi per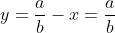
con un piccolo dubbio su questo ultimo passaggio.
più o meno é questo Fabrizio; io uso diverse notazioni e poi il principio di induzione su h. Ma il concetto è questo
caro Umberto,
forse non ci siamo capiti... io intendevo dire che sostituire x con a/b - x all'interno della funzione e' un gioco da ragazzi... e mi sembrava inutile esprimere il conto per esteso... Chi conosce le derivate e -magari- i coefficienti binomiali deve per forza essere in grado di fare quella banale sotituzione di incognita e operare le semplificazioni del caso...
Comunque, nessun problema...
neanche per me. In effetti io intendevo proprio di esplicitare il calcolo, non so se tutti lo avevano presente
Ok, possiamo chiudere qui. Per ora le risposte possono essere ricercate nei commenti. Ci aspettano ancora solo due (spero) miniquiz, dopo di che il tutto verrà assemblato con le soluzioni a volte scritte da me e a volta tratte dai commenti. Questo primo esperimento di miniquiz atti a creare una sequenza che ci porti ad un risultato finale mi piace; è un modo per condividere assieme la dimostrazione di un teorema di grande importanza spezzettandolo in tanti semplici pezzi, e discutendo assieme su di essi.