Categorie: Matematica Quiz
Tags: cammino ottico quiz soluzione meccanica superficie sferica
Scritto da: Vincenzo Zappalà
Commenti:13
QUIZ pratico: “sporchiamoci le mani” e scartiamo la matematica… ***
Basta con equazioni, numeri, funzioni, trigonometria, algebra, geometria analitica… è arrivata l’ora di “sporcarci le mani”, come facevano i grandi geni dell’antica grecia e non solo. Eccoci di fronte a un problema da risolvere "meccanicamente" e -magari- costruire con le proprie mani.
Parlando di pi greco e di quadrature varie abbiamo capito che gli antichi “geometri” dovevano ottenere le loro scoperte attraverso strumenti meccanici, dato che la geometria analitica era ancora ben lontana dal venire in aiuto per la risoluzione dei vari problemi. Noi abbiamo la abbiamo spesso usata per dimostrare velocemente le geniali deduzioni di tanti secoli fa, ma , in realtà, le varie curve potevano essere tracciate solo meccanicamente. Non dimentichiamoci che lo stesso Archimede utilizzava prima le sue leve, e la bilancia in particolare, per determinare l’equivalenza di superfici e di volumi.
Cerchiamo, allora di imitarli… (ne siamo ancora capaci?). Dimentichiamoci, perciò, la geometria analitica e affrontiamo un bel problemino con mezzi soltanto meccanici, ossia costruiamo uno strumento che ci permetta di risolvere il quesito in oggetto. Dato che ci stiamo interessando particolarmente della geometria proiettiva cosa c’è di meglio che affrontare un problema di ottica? Gli antichi, pur non sapendo cosa facesse vedere un oggetto, se un qualcosa che andasse dall’occhio all’oggetto o viceversa, né tantomeno cosa viaggiasse tra oggetto e occhio, avevano già capito molto del tragitto effettuato dalla … luce. Basta ricordare, tra le tante deduzioni, gli specchi ustori di Archimede…
Bene, il problema che ci poniamo è qualcosa di abbastanza simile, ma che abbisogna di uno strumento costruito per lo scopo:
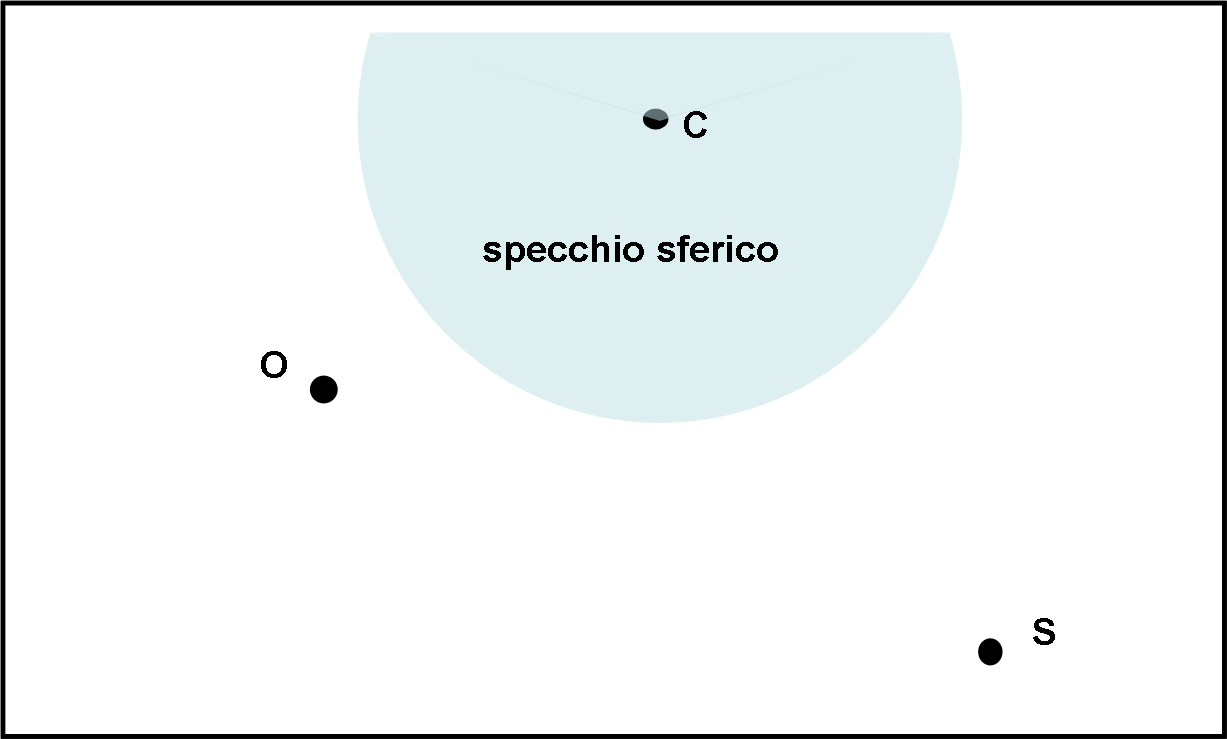
Fissiamo un certo oggetto S (sorgente luminosa, in parole moderne) e poniamo il nostro occhio in una certa posizione O. Vogliamo costruire il cammino ottico da S a O, dopo una riflessione sopra una superficie sferica. In altre parole, vogliamo determinare il punto P in cui la luce di S si riflette sullo specchio circolare per giungere in O.
La Figura che segue illustra la situazione di partenza (C è il centro dello specchio sferico).
Ovviamente, tutti sappiamo cosa deve fare il raggio luminoso durante una riflessione, ma noi non vogliamo certo andare avanti per tentativi, bensì costruire uno strumento che ci permetta di eseguire poche azioni ben stabilite in modo da essere sicuri di ottenere il risultato finale.
Chi (vero Arturo o Maurizio?) ama toccare le cose con le proprie mani, potrebbe costruire veramente il meccanismo richiesto. Tuttavia, basta anche solo un disegno schematico con le giuste spiegazioni per utilizzarlo…
E’ giunta l’ora di sporcarci le mani e abbandonare coordinate, equazioni, derivate e integrali… forza miei prodi!
QUI la soluzione






13 commenti
Si può ragionare nel piano passante per C ? Cioè, ok lo specchio è sferico, ma la riflessione avviene secondo il piano S-C-O (a cui apparterrà anche P).
Se così fosse, così di getto mi viene che la bisettrice dell'angolo SPO deve passare per C (angolo di incidenza = angolo di riflessione). Quindi bisognerebbe escogitare un arnese che facendo muovere l'ipotetico punto P lungo la circonferenza (sezione della sfera con il piano di riflessione) mi traccia automaticamente la bisettrice. Quando, muovendo il punto lungo la circonferenza, la bisettrice passa proprio per C, avremo trovato il punto di riflessione. Ma vallo a escogitare un tracciatore manuale di bisettrice dati due punti e un vertice variabile dell'angolo.. Si potesse usare il compasso sarebbe facile, ma una circonferenza per volta...
Pensandoci su, un attrezzo adatto potrebbe essere quello raffigurato qui:
(chiedo venia per l'uso del solito programma per fare il disegno, ma si sa, a monte della realizzazione di un qualsivoglia utensile, ci deve essere un minimo di progetto... )
)
L'ho chiamato "pantografo bisettore". Non so sinceramente se esiste già. In pratica è formato dalle aste nere per i punti F, Px, H, K e dall'asta rossa. Nei punti F, Px, H e K le aste sono incernierate. Inoltre, in K e Px c'è un cilindretto in cui passa l'asta rossa. In K l'asta rossa è anche libera di scorrere. In sostanza, aprendo o chiudendo il pantografo, cioè variando l'angolo OPxS (le aste nere più lunghe sono otticamente allineate ai punti O ed S dati dal problema) , cioè in definitiva spostando Px lungo la circonferenza, l'asta rossa (bisettrice) si sposta a destra o a sinistra del punto C. Quando passa per C, avremo trovato il punto P di riflessione.
Tutto quanto sopra sempre che sia lecita l'ipotesi fatta, cioè di lavorare nel piano , e sempre che l'accrocco funzioni realmente, cosa non scontata, data l'ora tarda
Non rispondo ancora... aspetto alternative di altri maghi meccanici... Tu, comunque, puoi cominciare a costruire un prototipo e vedere se funziona facilmente...
L'idea di Arturo mi sembra geniale. Suggerirei per la costruzione di utilizzare un vecchio ombrello come struttura di partenza.
Ovviamente, la sezione piana è accettata, dato che la riflessione avviene in un piano passante per il centro della sfera...
L'opzione migliore (secondo me) è FISSARE una parte del meccanismo al centro C... in modo che possa ruotare intorno a lui... descrivendo un moto circolare....
Si, caro Enzo, è opportuno aggiungere un'asta C-Px, incernierata ai due estremi, in modo che il punto Px sia vincolato a muoversi lungo la circonferenza. Il suggerimento di Mau sul vecchio ombrello è ottimo, però vorrei cimentarmi in una completa autocostruzione. Vedrò se riesco a trovare delle asticelle di legno, materiale molto malleabile anche con i mezzi normalmente a disposizione in casa.
Poi, buttando l'occhio sul metro laser che uso spesso per lavoro pensavo che sarebbe di una banalità unica usarlo per tracciare il punto di riflessione P, come da due figure allegate:
Basterebbe metterlo in uno dei due punti S oppure O , accenderlo e ruotarlo fino a che il raggio , riflettendosi sulla superficie curva a specchio, non va a passare dall'altro punto. In quel momento, sulla superficie curva vedremmo il punto rosso di riflessione del raggio laser. Ma così sarebbe troppo facile e per niente "antico". Però, magari, se al posto del laser si usassero gli specchi ustori di Archimede al contrario ?
grande Artimede!!! Pensa anche a dove sia meglio mettere il "rombo" ... Sapevo che avresti tentato la costruzione... posso solo dirti che si era anche cimentato il grande Leonardo!!!
vertice A fino a incontrare la superficie dello specchio, poi si ruota il rombo, mantenendolo tangente al cerchio, fino a puntare sull'osservatore vicino , poi si stringe o si allarga il rombo agendo sul segmento AC fino a puntare l'oggetto astronomico lontano.
Tutto ciò presuppone che lo specchio sia accessibile e che si possa puntare il lato AD in direzione dell'oggetto astronomico lontano.
Il rombo va bene... ma.... io lo inserirei in un'altra posizione... In ogni caso oggetto e occhio sono entrambi vicini alla sfera... nessun problema di lunghezze di aste.
ATTENZIONE: forse la parola sfera vi ha bloccato in qualche moso... chiarisco meglio la situazione. Una volta assodato il fatto che tutto si svolge su un piano, possiamo tranquillamente lavorare su di esso e quindi il centro del cerchio e il suo raggio diventano cose "tangibili"...
Il succo ormai è stato raggiunto. La soluzione "ombrello" o -meglio- rombo è l'idea di base, unica figura che permette di mantenere gli angoli uguali pur variando forma...
Adesso aspetto solo una foto dell'attrezzo realizzato. Dai Leandro provaci anche tu!
Tra un gocciolatoio e l'altro ....
Naturalmente ogni giunto consente una rotazione delle aste e i manicotti scorrono lungo l'asta centrale. Direi che funziona bene.
Ottimo, caro Mau (c'avrei giurato che non avresti perso l'occasione!). Io direi che si può anche fissare un supporto esterno al punto S con un'asta che possa liberamente scorrere da entrambe le parti. Muovendo l'asta libera fino a farla coincidere con il punto O, si ottiene il percorso voluto. Il rombo fa da fisarmonica e si trascina il punto P sulla circonferena.
In realtà, il rombo potrebbe tranquillamente stare all'interno della circonferenza, senza dare fastidio a chi volesse tracciare il perorso SPO.
Per adesso siete in tre concorrenti e il miglior realizzatore vincerà il premio consistente in una corrona di alloro!!!
Ecco la modifica suggerita da Vinenzo. Un manicotto girevole nel punto S non si nega a nessuno....
Gli elementi sono stati riassemblato scambiando ( molto facilmente e velocemente) le connessioni. Eventualmente il rombo potrebbe essere ricostruito con lati più piccoli.
Io pensvo a un rombo che degeneri nella distanza OP (caso S=O) e in un segmento perpendicolare (SPO = 180)
Direi che è vero il detto "mani grosse e cervello fino!"