QUIZ: I pappidi e l’ostacolo improvviso **
Un quiz matematico-geometrico che potrebbe servire come esercizio in vista dei prossimi esami di maturità. Non un vero problema, ma solo un quesito o poco più…
Mai fidarsi dei professori con lo sguardo diabolico… Nobody aveva promesso di lasciare stare i nostri tre fratelli, ma la rabbia è stata più forte. In realtà, non mette a repentaglio la loro vita, ma cerca di rendergliela difficile.
Ogni giorno Peppa, Pippo e Pappo si recano da casa loro (A) all’ufficio (B), attraversando un vastissimo prato verde. La distanza in linea retta è di 2 km. Per mesi e mesi, i nostri amici fanno la loro passeggiata mattutina di 2 km.
Un brutto giorno, ecco comparire il solito Nobody che gli comunica che il loro percorso diventerà più difficile. Il 50% delle volte che percorreranno la strada, tutto sarà tranquillo e normale… ma il 50% delle volte, esattamente a metà strada (in C), si formerà un ostacolo invisibile, ma invalicabile, formato da un materiale resistentissimo di sua invenzione, che bloccherà la strada per 1 km sia a destra che a sinistra, in modo che l’unica possibilità sarà quella di girargli attorno e allungare di molto il percorso.
La Fig. 1 riassume la situazione.
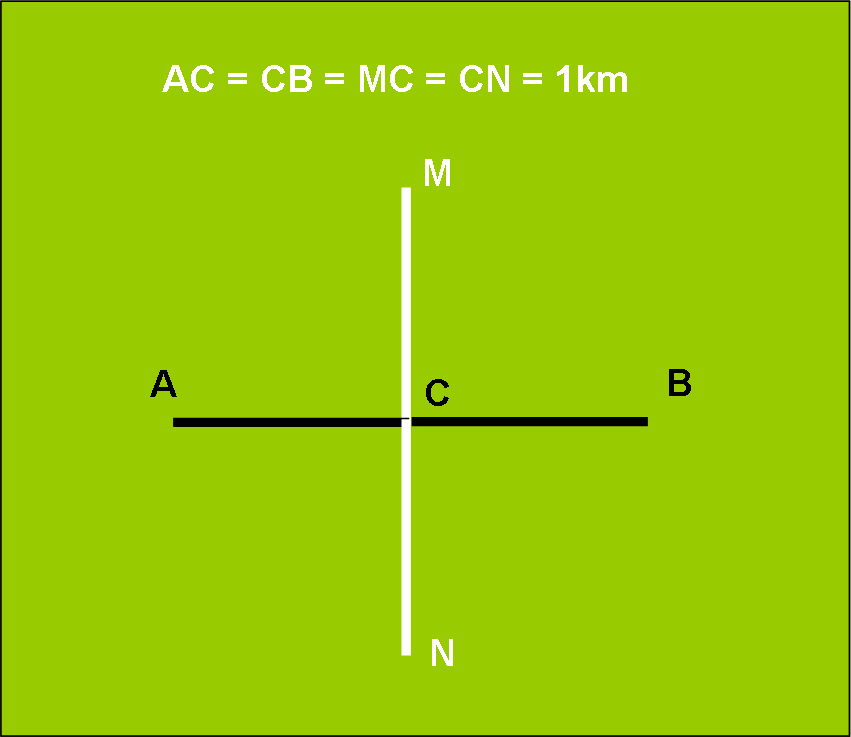
Nobody sfida i fratelli a effettuare il percorso medio più corto possibile. Se ci riusciranno, promette che non li disturberà più… (ma chi ci crede?).
Ovviamente ci riescono… Qual è il percorso che devono compiere?
QUI la soluzione
QUI altri percorsi da calcolare!
44 commenti
Di primo acchito vedo un percorso standard che ha una lunghezza fissa pari al 94% di quella media ottenuta dal percorso iniziale che nel 50% dei casi viene raddoppiato per via dell'ostacolo imprevedibile e insormontabile.
Niente disegni per lasciare il piacere di ragionarci su agli altri lettori.
Non è detto che non si possa trovare di meglio
Seguendo la strada solita, ogni due volte si perde 1,4142 Km circa
L’altra in diagonale 1,658 Km
Una un poco inclinata 0,4142 + 0,077*3 + 0,6 =1,245 Km, sempre ogni due volte
Più inclinata 0,4142 + 0,118*3 + 0,5 = 1,268 Km
ma nel caso sfortunato perché il percorso dovrebbe essere raddoppiato? Il prato è percorribile a quindi si tratta di camminare lungo due diagonali.
Se ho ben capito il problema, si tratta di partire da N e puntare ad un opportuno punto intermedio tra A e C ( o se preferite tra C e B) e da esso ripartire verso M.
La scelta del punto intermedio che chiamiamo X deve minimizzare la media dei due percorsi con e senza ostacolo.
Facendo i conti, il percorso medio dovrebbe essere il 91,13% di quello medio ottenuto da percorso netto di 2 e ostacolato di 4.
Taccio sul valore che deve avere la distanza CX.
Leandro, il percorso lungo le diagonali a 45 gradi non è ottimale. Esiste una diagonale più breve che accorcia il cammino se non c'è ostacolo e lo allunga in modo limitato se l'ostacolo compare.
E una questione di minimizzazione.
minimizzate, minimizzate... ma pensate ai maturandi (che provino anche loro...!)
Certo che Nobody poteva pensare a una distribuzione di probabilità più complicata...In fondo è un cattivo buono.
vi prego solo di non andare per tentativi... Per la maturità bisogna conoscere certe operazioni...
Per esempio lo studio di funzioni
E le derivate... E il loro utilizzo per trovare i..
Basta!
silenzio e mobilitate tutti i maturandi che conoscete!!!!! chissà che qualcuno non riesca a trovare il coraggio di risolverlo?
Scegliendo bene il percorso nel tratto finale dopo l'ostacolo si scende sotto il 91,13%...
Salvo errori, il percorso migliore ha una lunghezza 87,3% di quello che prevede la distsnza di 2km in caso favorevole e di 4km in caso sfavorevole, ossia andando sempre a "vedere" fino al punto C.
Mi torna 87,3% del percorso medio ma non ottimale.
Il minimo che si può fare rispetto alla soluzione banale è 97%
La mia interpretazione, tenendo conto che:
"Un brutto giorno, ecco comparire il solito Nobody che gli comunica che il loro percorso diventerà più difficile. Il 50% delle volte che percorreranno la strada, tutto sarà tranquillo e normale… ma il 50% delle volte, esattamente a metà strada (in C), si formerà un ostacolo invisibile, ma invalicabile, formato da un materiale resistentissimo di sua invenzione, che bloccherà la strada per 1 km sia a destra che a sinistra, in modo che l’unica possibilità sarà quella di girargli attorno e allungare di molto il percorso.
Se continueranno a compiere lo stesso percorso rettilineo AB, il 50% delle volte si renderanno conto dell’ostacolo solo quando arriveranno in C."
https://i.imgur.com/GQ3hI07.png
https://i.imgur.com/wwuNu8i.png
Ok, vedo che concordiamo con Leandro e Andy.
Si può fare il calcolo anche senza usare le funzioni trigonometriche, se a qualche maturando non piacciono.
Ma cosa staranno facendo..?
Staranno studiando per la maturità... se no che maturandi sono?!?
gradirei che mi deste il risultato in km... All'inizio sono 2 km. Dopo Nobody... quanti km devono fare ogni giorno per fare il percorso mediamente più corto? Ovviamente, ogni giorno devono ripetere lo stesso nuovo percorso... lasciate stare le percentuali... km voglio km!!! ( il disegno del percorso...).
Con la barriera passano 0,3546 Km al di sopra di C , poi per M e poi verso B, percorrendo 3,120623 Km
Senza barriera vanno direttamente dal punto al di sopra di C al punto B e sono 2,122019 km
La media è pari a 2,621321 Km
scusa Andy se mi intrometto, ma non capisco perché complicarsi la vita con angoli e funzioni trigonometriche che poi sono anche difficili da studiare. Per me basta il teorema di Pitagora per impostare la funzione. E poi, come richiesto dal quiz perché esprimere una percentuale? E' richiesto un percorso e la sua lunghezza.
Sono d'accordo con te, Umberto, basta Pitagora. in quanto alla "colpa" della percentuale è tutta mia, ho cominciato nel mio primo commento. Andy e Leandro hanno cortesemente continuato a parlare in termini di percentuale solo per confrontarci.Lo scopo era solo di dare una idea di quanto una scelta mirata consentiva di migliorare il risultato
E' scoccata l'ora della mia figuraccia quizzo-pappica, quindi riporto il mio inutile tentativo di calcolare il punto di minimo della funzione "percorso medio dei pappidi" (partendo dalla figura postata da Mau).
Prima di trattarmi male
, sappiate che ho solo provato ad aprire qualche arrugginito cassetto della memoria, così... quasi d'istinto... quello che vorrei sapere da maghi e affini è se ho compiuto errori di concetto o solo di calcolo.
temo ci sia qualcosa che non va...
caro Pautasso, qualche calcoletto in più....? Intanto , ho visto che i maturandi sono ancora ... acerbi...
cara Dany... in una derivata hai perso un pezzo per strada...
Ok, grazie, dovrò comprare un efficace antiruggine per trovare il pezzo mancante
comunque, se il problema è “solo” quello, mi ritengo moderatamente soddisfatta del risultato (per la serie “chi si accontenta gode”)!
funzione di funzione....
percorso favorevole l1=
percorso sfavorevole l2 =
percorso medio =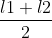
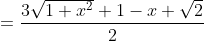
derivando e uguagliando a zero ...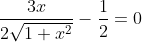
semplificando e quadrando...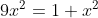
ricavo x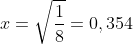
(Km)
sostituendo x nella espressione del percorso medio trovo il valore del percorso più breve = 2,621 Km
Per me, la trigonometria è la più bella che ci sia
Appaiono funzioni trigonometriche che possono creare difficoltà? No problem
Riprendendo la formula che calcola il percorso medio più breve in funzione di α:
che è la stessa espressione trovata da Oreste; seguendo lo stesso percorso di derivazione, uguaglianza a zero e semplificazione, si ottiene:
in linea con quanto calcolato prima, accontentando sia i "pitagorici" che i "trigonometrici".
ottimo Andy! La maturità è assicurata
Se hanno probabilità del 50%, su 100 giorni, percorreranno (mediamente):
(2 x 50 + 4 x 50) / 100 = 3 km
se, tutti i giorni fanno il percorso AMB (o ANB) percorrono 2,82 km che è il percorso medio più breve (in quanto l’ipotenusa è sempre più corta della somma dei cateti).
la mia non era una critica Andy, ma solo una osservazione. Per me si può fare a meno della trigonometria ,tutto qua. Ognuno è libero di risolvere un problema a suo modo, L'importante è il risultato. Ma una regola fondamentale della matematica è questa: la semplicità. Capirai che i conti che fa Oreste sono molto più sbrigativi e immediati. Comunque complimenti ,come al solito hai sviscerato il quiz.
caro Gianni,
si può fare di meglio...
Scusa Umberto,
ma quello della semplicità, a mio modesto avviso, è più corretto qualificarlo come criterio o modus operandi ottimale finalizzato in funzione della minimizzazione della quantità di tempo e/o passaggi interconnessi tra loro per giungere alla soluzione di un qualsiasi quesito/problema, perché una regola è un dettato che traccia dei limiti operativi netti ed oggettivi, valicati i quali si ricade nell’infrazione della regola stessa. Io intendo il quiz non come una gara a chi è più bravo o più figo o più veloce, ma come una costruzione che si basa e si sviluppa sul contributo di chiunque vi partecipi, apprezzando e traendo spunto da ogni singolo intervento:
vedi la riflessione di Maurizio circa i rapporti percentuali tra un percorso ed una altro preso come riferimento, fornendo utilissime indicazioni, o l’equazione presentata da Daniela cronologicamente prima rispetto alla stessa ricavata da Oreste e mirabilmente studiata dallo stesso, o le indicazioni “intrinseche” o “estrinseche” che Enzo fornisce sempre per dare input utili alla risoluzione del quiz stesso.
Ora, uno dei modus operandi applicabili non solo alla matematica ma a tutte le discipline in generale è quello della scelta, ove esista, di un’alternativa, sinonimo di una libertà di azione, la cui attuazione conduca al raggiungimento di uno stesso obbiettivo, nella fattispecie, la risoluzione di un quiz.
Se osservi, i passaggi per determinare il percorso libero e quello ostacolato e poi una loro media aritmetica, sono esattamente gli stessi in numero, sia che l’equazione della media è in funzione di una misura lineare, sia che l’equazione della media è in funzione di una misura di ampiezza. Ma dato che sarebbe estremamente difficoltoso studiare una funzione che contenga al suo interno delle funzioni trigonometriche, ho svolto solo 2 semplici e rapidi passaggi in più:
1. utilizzo di una identità trigonometrica che discende direttamente da una delle relazioni fondamentali trigonometriche, figlia dell’applicazione del teorema di Pitagora al triangolo rettangolo, calcolando i cateti in funzione dell’ipotenusa e ad uno qualsiasi degli angoli complementari;
2. uguaglianza di una funzione trigonometrica ad una variabile di primo grado e sostituzione della stessa nell’equazione principale contenente funzioni trigonometriche,
ottenendo la stessa espressione in funzione di una misura lineare, il cui studio è certamente più agevole rispetto ad un funzione contenente altre funzioni trigonometriche.
Pensi che si possa “aggettivamente qualificare” che i tempi di ottenimento dell’equazione in funzione di x senza il passaggio di trasformazione da α ad x come poc'anzi esposto siano “molto più sbrigativi e immediati”? Io no, limitatamente al “molto”.
Ad ogni modo, la mia non è polemica ma solo una riflessione; apprezzo i tuoi complimenti e traggo spunto per ricambiarli.
W la libertà!
come ti dicevo prima, Andy, la mia non voleva essere assolutamente una critica, ma solo un consiglio, una osservazione. Se tu ritieni di non averne bisogno buon per te.Non succederà più.
Un piccolo consiglio a Daniela: per semplificare i calcoli quando minimizzi una funzione puoi eliminare a priori divisori e termini additivi che non mutano l'ascissa del minimo funzionale.
Ok, grazie Leandro. In questo caso cosa avrei potuto semplificare?
Cara Daniela puoi eliminare il divisore 2 , poi elimina 1 e la radice di 2 che sono costanti.
Ti rimane solo
da cui ricavare la semplice derivata e uguagliarla a zero.
Questo è il metodo più intuitivo ma forse ce n'è uno più diretto
Certo, si tratta di costanti la cui derivata è pari a zero. Grazie!
sempre più divertente.....
detto a il segmento x, cioè l'ipotenusa di ACX
dobbiamo minimizzare
f(x)= (2a + a + 1 -x)/2
cioè ,più semplicemente
f(x)=3a(x) -x
derivando in x ed azzerando
3 a'(x) -1 =0
da cui
a'(x) = 1/3
cioè a(x) = x /3 , l'ipotenusa è 3 volte l'altezza x.
ma
quindi
(a+x) (a-x) =1
sostituendo da a il suo valore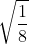
(3x+x)(3x-x) =1
4x 2x =1
quindi x =
invece entrando nel magico mondo trigonometrico
alfa = arsin (1/3) = 19.471 gradi
ma allora x = tg(alfa) = 0,3535 che è circa rad(1/8)
bravo Leandro... una bella dimostrazione di come ci si possa divertire con la geometria! Imparate maturandi... imparate!!!
Sarà l'ora tarda, ma mi è balzata in mente un'idea bislacca:
guardando il percorso AC'+C'M+MB, ai fini della media, il tratto più battuto è AC' = C'B = c, percorso complessivamente 3 volte (2 volte nel percorso libero AC' + C'B, una volta AC' nel percorso ostacolato) e quindi quello che dovrebbe incidere di più nel calcolo della media; mi sono allora chiesto: perché non minimizzare il perimetro del triangolo rettangolo ACC', visto che contiene il tratto di percorso più battuto, tenendo conto che l'altezza CC' = a dipende dalla misura di AC' e conseguentemente il tratto di percorso C'M misura la differenza a 1, e potendo manovrare solo su questi segmenti dato che la lunghezza di AC = b è costante e pari ad 1 km?
Ho parametrato la somma di a e c alla parte di percorso ostacolato, ma costante e di minima distanza tra i punti M e B:
MB = √2
Coincide con le soluzioni già fornite, ma non chiedetemi perché ciò avvenga, perché tra sonno e stanchezza non saprei come rispondere
Ciao Andy, il fatto che il risultato finale corrisponda a quanto trovato con le precedenti soluzioni dipende, secondo me, dalla circostanza che nella prima equazione hai assegnato:
c+a = √2
Evidentemente questa relazione è implicita nelle soluzioni, ma non trovo una giustificazione per scriverla a priori.
Quando parli di minimizzare il perimetro del triangolo rettangolo ACC' di lati a, b, c ( con b =1 ) immagino che la variabile consista nella scelta del punto C' , più o meno distante da C. Ma, in tal caso, il minimo perimetro lo otterresti con un C' coincidente con C (il triangolo si ridurrebbe ad un segmento sovrapposto a sé stesso e il perimetro varrebbe 2.
Caro Oreste,
perfetto e ineccepibile ciò che scrivi. Effettivamente ha poco senso parlare di un perimetro minimo, meglio considerare come una misura ottimale ai fini della minimizzazione di una media, della spezzata AC' + C'M, che varia da un minimo di 1, quando C' coincide con C e C'C si riduce ad un punto, ad un massimo di √2+1 quando C' coincide con M.
Lo dico a me stesso, è la derivata di una funzione che indica un eventuale punto di minimo/massimo, così come l'uguaglianza a 0 della derivata prima della funzione di medio percorso ha permesso di ricavare il punto di minimo in base al valore della variabile nella funzione derivata, determinando che la misura AC' + CC' fosse uguale a √2.