QUIZ: Il deposito del formaggio.
Altro che ferie: dopo a essere riuscito a visitare tutti i negozi dell'isola di Groviera, il topo logico si sente un po' stanco per tutti gli spostamenti fra i vari negozi, e pensa : non dovrò fare tutta questa fatica per sempre? Ormai sono vecchio, ho bisogno di costruirmi una pensione che mi permetta di vivere agiatamente mangiando tutto il formaggio che voglio senza fare fatica e senza rischiare di essere mangiato da un gatto.

Il nostro topo, girovagando per i negozi, è venuto a conoscenza dell'esistenza di un colossale deposito di Parmigiano, ma di preciso sa solamente la via , ma non il numero civico. Per ragioni di sicurezza, visto l'elevato valore del deposito, esso non ha alcun tipo di insegna, e solo i trasportatori scortati dalla polizia locale, sanno dove si trova. La via del deposito è molto lunga, e per il topo-logico sarebbe pericoloso cercare di visitare tutti i capannoni. Ma il topo non si arrende e per qualche settimana diventa un topo... di biblioteca.

Lì si mette a leggere tutti i giornali dell'epoca, finchè scopre che il deposito è stato eretto a scopo monumentale in onore di Don Alfonso di Groviera, formaggiaio e anche abile matematico.

Viene poi a conoscenza che il numero civico del deposito si può ricavare da una formula, che però è segreta. Indiscrezioni dell'epoca rivelano però che si trova in una posizione veramente matematica; infatti la somma di tutti i numeri civici che la precedono e quella dei numeri che la seguono è uguale! Si conosce inoltre l'ultimo numero della via dalla stessa parte del deposito, che è 337.Il topologico si mette subito a fare uno schema del problema:
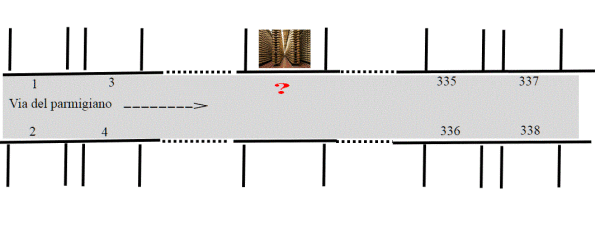
e dopo abili conti, riesce a trovare il numero richiesto. La sua pensione è assicurata!
Qual' è il numero civico del deposito e che calcoli fa il topo-logico per trovarlo?
Il quiz è aperto a tutti; magari i più esperti potrebbero mettere solo la soluzione numerica in un primo tempo, poi il procedimento. Comunque starà a loro decidere.






23 commenti
suppongo i numeri sullo stesso lato della strada (ossia i dispari)... o tutti indistintamente?
no no. Sullo stesso lato. Ma non è chiaro nel testo?
Diciamo così che è ancora più chiaro...
"...infatti la somma di tutti i numeri civici che la precedono e quella dei numeri che la seguono, nello stesso lato della strada) è uguale!..."
Forza, tanto per rimanere in tema, basta saper "quadrare" (anche se non è un cerchio...).
sarebbe un po' difficile sapere quali numeri precedono e quali seguono dall altra parte. Comunque cosi sarà meglio per tutti.
Il topo-logico sta già sgranocchiando groviera al civico 239.
non ricordo il risultato numerico..intanto grazie Maurizio
sbaglio se inizio a scrivere qualcosa del genere...
((1 +N -2)k)/2 = ((N+2)+ 337) (169 - (k + 2 ))/2
con N il numero del deposito
poi c'è solo da sistemate k ...
Purtroppo non posso stare troppo con gli occhi fissi in basso...
?????
non so.. dovrebbe bastare una variabile però
sì... ma k è funzione di N... se domani va meglio cerco di scriverla completa...
non c'è fretta..sono demolito anche io dal caldo
Partendo da 1, la somma dei primi n numeri dispari - a cui corrisponde il numero dispari Z - è n^2. La somma dei dispari precedenti è quindi ((Z-1)/2)^2. La somma dei successivi è ((337+1)/2)^2-((Z+1)/2)^2. L'uguaglianza tra le due quantità restituisce Z
ciao Enrico, ma quanto varrebbe Z?
c'è qualcosa che non mi torna... forse sarà l'occhio...

l'ultimo numero civico è il 337 che corrisponde al 196esimo numero dispari. O sbaglio? Se è così non mi torna la metà esatta...
Avevo provato cercando di imitare Gauss, ma è molto più semplice... però qualcosa non va. Sto facendo un errore e non me ne rendo conto...
I primi k numeri dispari danno come risultato quello che sappiamo. Ma a noi interessano i primi k-1 numeri dispari e poi i numeri dispari che vanno da k+1 fino alla fine della strada... o invece bisogna considerare i secondi che vanno da k fino alla fine????
la prima opzione. K é escluso
Ok, OK... il k= 1 è quello che è... e quindi il numero magico è 14161!!! Ne avevo saltato 1, non si parte da k + 1, ma da k... Temo che sia la testa non gli occhi!!!!!

Il numero 337 occupa il 169 esimo posto tra i numeri dispari
(1+337)/2 = 169
la somma dei dispari fino a 337 vale 169^2
a questa somma tolgo il valore di X , numero civico del formaggio
la somma dei numeri dispari "prima di X" vale la somma dei numeri dispari "dopo X" e ambedue valgono
(169^2 -x )/2 = ( ( 1+x-2) /2) ^2 = (x^2-2x+1)/4 dove x-2 è il numero dispari che precede x
ora posso ricavare x ...
2*169^2 -2x = x^2 -2x +1 da cui, semplificando
x^2 = 2*169^2 -1 e quindi
x= √ (2*169^2-1) = √ 57121 = 239
se calcoliamo la somma dei dispari fino a 237 ... ((1+237)/2)^2 = 14161
come controprova ... raddoppiando e sommando 239 otteniamo 14161*2 + 239 = 28561 = 169^2
Buon appetito, Topo-Logico
ma come fai mau/pau ad essere così in forma oggi? Io sono qua che beccheggio. E l aria della costa Smeralda? O vai a respirare solo ossigeno come faceva M. Jackson?
Il segreto , Umberto, è nella doppia personalità, mentre uno pensa l'altro dorme. Però non sempre funziona, qualche volta risponde quello che dorme.
Ciao Umberto,
vedi la spiegazione di Oreste. Lui si è preoccupato di essere più chiaro di me
Ma ci tento anch'io ora:
"Partendo da 1, la somma dei primi n numeri dispari - a cui corrisponde il numero dispari Z - è n^2".
Es. la somma dei primi n=5 numeri dispari (il quinto numero dispari essendo Z=9) è 5^2.
Il resto vien da se...
ok Enrico guarderò più a fondo .Grazie
Mi permetto di inserire due figure che dovrebbero spiegare bene la soluzione da scegliere e l'errore che si può commettere (l'ho fatto anch'io in un primo momento...)
VERSIONE SBAGLIATA
VERSIONE GIUSTA
In un primissimo momento avevo cercato di imitare Gauss bambino, ma l soluzione era decisamente più facile lavorando solo su k....
ok grazie
"...ma la soluzione era decisamente più facile lavorando solo su k"
E ancor più facile usando la sommatoria di Excel !!!

(ok, ok... vado ad imbarcarmi sul primo razzo in partenza per Papalla )
)