Categorie: Matematica Quiz
Tags: numeri positivi interi quadrato quiz
Scritto da: Vincenzo Zappalà
Commenti:23
quiz sul quadrato perfetto... **
No, non voglio fare concorrenza a Umberto, ma mi permetto di prospettare un facile quiz da "spiaggia" che, sicuramente, offre molte soluzioni... Vediamo chi ci regala la più elegante e/o rapida ?
La domanda è presto fatta:
Trovare TUTTI i numeri n, interi e positivi, tali che n2 + 45 sia un quadrato perfetto.
Ovviamente non vale andare per tentativi... ma bisogna trovare una relazione che permetta di calcolarli
La soluzione matematica è stata abbondantemente sviscerata nei commenti. Resta sempre aperta una visione più geometrica...
23 commenti
e uno....
la scelta di a è però fatta per tentativi?(anche se pochi)...
Mi sembra che la scelta di a non sia per tentativi. Sono tutti i sottomultipli di 45 che producono n>0.
beh... sì, hai ragione... come non detto
un metodo diverso
m^2-n^2=45
(m-n)(m+n)=45 quindi si tratta di risolvere il problema: Trovare due numeri di cui di conosce la somma e la differenza. Può essere infatti
scusate quella citazione blu non era voluta. Non so come sia saltata fuori
e due (questa era anche la mia...)
Ho provato a generalizzare il risultato ottenuto per 45 ad altri numeri interi.
L'espressione che si ottiene è la stessa con la sostituzione di 45 con un numero intero generico.
Se M è un qualsiasi intero dispari vale la soluzione trovata per 45: a è un qualsiasi divisore di M che mantenga n>0.
Se M è pari la cosa si fa più articolata. a non può essere un divisore dispari altrimenti l'espressione tra parentesi è dispari ed n non sarebbe intero (es. M=60 a=5, n=3,5 che non va bene). Per la stessa ragione non può essere neanche un divisore pari che contenga tutti i 2 disponibili (es. M=60 a=4, n=5,5).
Per fare in modo che n sia intero a può essere un qualsiasi divisore pari di M che non contenga il fattore 2 al massimo esponente. Questi divisori esistono solo se M è divisibile per 4.
Per M=60, n=14 per a=2, n=2 per a=6
Per M=30 invece non ci sono soluzioni
E provare l'altro metodo ? Ci voglio pensare, appena ho un po' di tempo... oppure può farlo anche Umberto o tu stesso.
be ma l altro metodo dovrebbe funzionare sempre.se invece di 45 abbiamo M generico dobbiamo solo scomporlo i fattori. In ogni caso poi dobbiamo vedere se n=(a-b)/2 é intero.
Buono il metodo diUmberto che mi sembra il più diretto anche se molto algebrico. Qualcuno ha trovato una soluzione geometrica?
io no ma mi sono chiesto anche io se esista
Io sono d'accordo con Umberto... per avere soluzione la differenza tra i due fattori (il maggiore meno il minore) deve essere un numero pari. Mi sa che da lì non si scappa...
O, in altre parole, i due fattori moltiplicativi devono essere entrambi pari o entrambi dispari... Ed è facile dimostralo...
Quali sono i numeri che ammettano una scomposizione in fattori o entrambi pari o dispari?
Che ne dite di studiare questa funzione? In fondo è la rappresentazione geometrica del quadrato di un binomio...
L'espressione che ho proposto,\frac{1}{2})
, è la stessa che ha utilizzato Umberto (scusate avevo scritto erroneamente Maurizio), infatti 
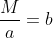. Abbiamo solo invertito il significato di a e b. Ho preferito scriverla in questo modo per evidenziare un solo fattore sul quale ragionare.
Arrivati a questa espressione, tutto il ragionamento che segue relativo agli M dispari e pari può essere lo stesso nei due metodi.
Io sono partito da^2)
invece che da m+n=b ed m-n=a perchè mi sembrava il metodo più diretto per arrivare alla espressione sopra senza passare per il sistema di due equazioni. Più una questione di gusti che una valutazione oggettiva.
Per quanto detto sopra, può essere evitata la verifica a posteriori che n sia intero anche per il metodo proposto da Umberto.
In risposta alla domanda di Enzo "Quali sono i numeri che ammettano una scomposizione in fattori o entrambi pari o dispari?"
Per le ragioni che ho scritto nel commento delle 10:33, sono i numeri M dispari o multipli di 4.
Mentre per i primi possono essere presi tutti i divisori a che portano ad un n>0, vale a dire
. Lo abbiamo visto con 45.
Per gli M multipli di 4, possono essere presi i soli divisori pari che non contengano 2 al massimo esponente.
Per M=60, n=14 per a=2, n=2 per a=6. Invece non vanno bene a=3 o a=4.
Per M=30 invece non ci sono soluzioni perché è pari, ma non è divisibile per 4.
per me le estensioni dei quiz sono sempre un po'..diaboliche! Se vogliamo un metodo per trovare tutte le soluzioni vanno bene gli algoritmi proposti. L altra domanda potrebbe essere; come deve essere fatto M per avere almeno una soluzione? E ' questa la domanda che vogliamo proporre?
le soluzioni sono quelle della conica... variando n... oppure si può mettere x come termine noto e vedere se ha o non ha soluzioni... boh... fate voi
Partendo da un quadrato di lato x è possibile (e quando) ottenere un quadrato di lato x+y? Che valore deve avere y? Siamo perfettamente all'interno del quadrato di un binomio...
Concordo, comunque, con Fabry che il metodo è uno solo... (la divisibilità per 4 per me è una conseguenza della sottrazione di numeri pari e dispari, forse potrebbe essere scritta in modo più matematico... non so)
Si è lo stesso metodo. Concordo.
scusate se faccio un ultima osservazione: Tutto torna con Fabrizio anche utilizzando l'espressione n=(a-b)/2 che deve essere intera, dove a,b sono tali che a*b=M; se cerchiamo quando è possibile l'equazione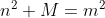
, nel caso in cui M sia dispari,, chiaramente possiamo scomporre M in a=M,b=1; essendo M dispari, M-1 è pari e quindi n=(a-b)/2 =(M-1)/2 è intero. Quindi una soluzione la troviamo sempre. Nel caso poi ,come dice Fabrizio, M=4*q, ossia è multiplo di 4, riusciamo sempre a scomporre in due interi che contengano entrambi il fattore 2; il loro prodotto è in tal caso M=(2*d) *(2*c) dove c e d possono essere anche 1. Abbiamo allora n=(2*d)-2*c) /2 che è intero, ossia divisibile per 2. Mi restava un dubbio: se M soddisfa alla condizione di divisibilità per 4, allora esiste sempre una soluzione, ma il viceversa? Ovvero, se M è pari e soddisfa l'equazione 
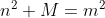allora è divisibile per 4?Non so se con il metodo di Fabrizio salti fuori subito. Supponiamo che valga 
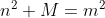, e che M sia pari. Esistono a,b tali che a-b sia pari, a-b=2*k1; a=2*k1+b; a*b=2*k1*b+
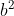; a*b =M è pari per ipotesi, ed essendo dato dalla somma di due numeri di cui 2*k1*b è pari, anche 
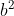deve essere pari. Ma b è un, intero, quindi deve essere pari. Ma allora 
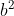è divisibile per 4, e anche 2*k1*b essendo b pari. Quindi M è divisibile per 4.
Boh.. vedete se va bene
So che non interessa, ma viene fuori un'iperbole equilatera del tipo x2 - y2 = a2 che, al variare di a deve dare almeno una y intera per tutti i valori interi di x... va beh... comunque consideriamo chiuso il quiz che necessitava solo una risposta numerica...