Un quiz logaritmico.
Scusate se mi permetto di scrivere un quiz che ha come argomento i logaritmi.. ma in fin dei conti penso che almeno la definizione di logaritmo la conoscano tutti. In fin dei conti qualsiasi scuola media-superiore li tratta . E a dir la verità restano impressi. Per risolvere il quiz è sufficiente conoscere solo la definizione di logaritmo.. e tanta fantasia!
Il quesito è semplice come stesura , ma può apparire inquietante. La domanda è la seguente:
?
OPPURE:
?
Chiaramente lasciamo da parte le calcolatrici.. siamo in un isola sperduta!
40 commenti
direi ai più esperti di soprassedere un pochino... o no?
penso che lo sappiano, grazie
ok il quiz è aperto a tutti, chiunque voglia può rispondere, o dare suggerimenti
Avrei questa possibile soluzione ...
mi aspettavo un approccio funzionale da un buon ingegnere; a dir la verità contiene anche un suggerimento per una dimostrazione ancora più rigorosa. Comunque per adesso non dico altro.
Anche la mia è una soluzione grafica, e parte dalla definizione del logaritmo. Allego la figura fatta a mano su quaderno a quadretti. Le due curve sono state disegnate per punti (per la prima : x=1-->y=2; x=2-->y=4 etc, così pure per la seconda). Potevo disegnarle più precise considerando anche i punti x=1/2 ---> y=radq(2), x=3/2--->y=radq(8) etc.
Ho pure provato a smanettare solo con i numeri e partendo sempre solo dalla definizione di logaritmo, ma il massimo che ho sinora ottenuto è che il prodotto dei due logaritmi dati è maggiore di 2 e minore di 3.
ok grazie Arturo
secondo me si può rispondere utilizzando le proprietà dei logaritmi, ricordando solo che la funzione log è crescente, ossia log 3 > log 2 e sempre maggiore di 1 per un numero maggiore della base qualsiasi base sia... quindi non ha bisogno di grafici...
scusa Vincenzo ma ho capito ben poco.. Quel log é un logaritmo in base e?
ho scritto log per qualsiasi base (positiva), quindi 2, 3, 5 , 10, e.... quello che si vuole... ossia logab > log ac se b > c. Tutto lì...Inoltre se b, c > a, log a> 1. Ma non avevi detto di aspettare..?
nella seconda riga loga>1 significa logab e logac > 1 ....
log2(3) =1/log3(2) per le proprietà dei logaritmi
pongo x= 1/log3(2) , y= log3(5)
si deve trovare se il prodotto xy è >1 o <1
riscriviamo
3^y = 5
3^x = 2
3^(x+y) =10)
3^(x-y) = 2/5
(tutti i logaritmi si intendono in base 3) cioè
x+y= ln 2 + ln 5
x-y = ln 10 - ln 2 -ln 5
sommando e sottraendo
2x = ln 10 + ln 2 -ln 5
2y = ln 10 - ln 2 +ln 5
osserviamo che
2< ln 10 <3
0 < ln 2 <1
1< ln 5 <2
da cui
0 < 2x < 3
2 < 2y < 5
cioè
0<x < 3/2
1< y < 5/2
da cui
0 < xy < 15/4 < 1
Il problema è che per fare il confronto occorre avere tutti i logaritmi nella stessa base. Ma quando si opera il cambio di base si introduce un terzo elemento.
Ad esempio: trasformo log3 (5) = log2 (5) / log2(3) passando alla base 2.
Ora il rapporto originale da valutare: log2 (3)/log3(5) diventa log2(3)*log2(3) / log2(5)
Pur sapendo che log2(5) > log2(3) , dato che ambedue sono maggiori di 1, non riesco a valutare se questo rapporto è maggiore o minore di 1, se non calcolando i valori dei logaritmi ( magari passando a quelli naturali e ricordando lo sviluppo in serie, oppure passando ai logaritmi in base 10 e ricordando i valori di logaritmo in tale base, per 2 , 3 e 5 )
ho scritto un passaggio ambiguo. Chiarisco:
(tutti i logaritmi si intendono in base 3 cioè
x+y= ln 10
x-y = ln 2 -ln 5
sommando e sottraendo
2x = ln 10 + ln 2 -ln 5
2y = ln 10 - ln 2 +ln 5
Per saper quale dei due logaritmi è maggiore occorre valutare il loro rapporto.
Se trasformo tutto in base 3, il rapporto diventa 1/( log3(5)* log3(2))
Pur sapendo che log3(5) > 1 e log3(2) < 1 non so se il loro prodotto è maggiore o minore di 1.
Non ho ben capito il ragionamento di Leandro in proposito.
scusa Vincenzo, ho aspettato un giorno. Poi ho dato il via. A dir la verità non avrei messo limiti, perchè secondo me è un quiz per esperti.
Scusa Leandro, non capisco anche io. Nella seconda riga del secondo commento hai scritto:
pongo x= 1/log3(2) , y= log3(5); però qui hanno la stessa base, nel testo uno è base 2, l'altro base 3. Ho c'è qualcosa che mi sfugge?
Nel disegno di Arturo si vede qual'è la soluzione vera, pur mancando dei calcoli appositi per dimostrarla.
Adesso ho visto Leandro, in ogni caso come Maurizio non vedo bene la conclusione.
purtroppo oggi non è giornata per me... ma temo di aver cantato vittoria troppo in fretta... devo studiare un'altra strada senza grafici...se riesco a fare qualcosa lo scrivo...
per le proprietà dei logaritmi
ove x=)
grazie,alla fine lo avevo visto. Premesso che devo fare tutti i calcoli, Ma perchè alla fine scrivi :
0 < xy < 15/4 < 1,
perchè 15/4 <1?
Cerco di riscrivere il tutto usando l'editor .
Si parte da
)
)
per le proprietà dei logaritmi un log è uguale all'inverso dello stesso purché si invertano base e argomento
infatti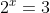
è equivalente a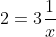 
pongo)
e )
quindi xy che è il rapporto dei due logaritmi iniziali può essere < o > di zero (zero escluso)
riscriviamo
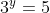
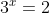
ora moltiplichiamo la prima per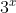
e la seconda per 
.
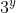si ottiene
tutti i logaritmi si intendono in base 3 cioè
x+y= ln 10
x-y = ln (2/5) = ln 2 - ln 5
sommando e sottraendo si ottiene il sistema (1)
2x = ln 10 + ln 2 -ln 5
2y = ln 10 - ln 2 +ln 5
osserviamo che
2< ln 10 <3 perché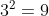
che è minore di 10 e 
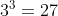è maggiore di 10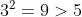
0 < ln 2 <1 perché 3 > 2
1< ln 5 <2 perché
da cui, analizzando il sistema (1)
0 < 2x < 3 = il massimo tra ln 10+ln 2 - ln 5
2 < 2y < 5 = il massimo tra ln 10 - ln 2 + ln 5
cioè
0<x < 3/2
1< y < 5/2
da cui
0 < xy < 15/4 < 1
scusate , moltiplicando
0 < 2x < 3 = il massimo tra ln 10+ln 2 - ln 5
2 < 2y < 5 = il massimo tra ln 10 - ln 2 + ln 5
mi è scappato un 4 :
0 < 4 xy < 15
0< xy < 15/16 <1
ok Leandro,adesso che le imprecisioni di scrittura si sono risolte potrebbe andare bene. Leandro è riuscito a ridurre in un caso particolare (base-argomento) alla stessa base. se così non fosse stato non ci sarebbe confrontabilità diretta. C'è però un sistema semplice, che si evince anche dal disegno di Arturo. Se non possiamo confrontare direttamente i due logaritmi con base diversa, possiamo passare attraverso un confronto indiretto.
Non dico altro, ma il tutto si risolve in una riga di calcolo.
non capisco l'ultimo passaggio di Leandro...
Io mi sono trovato nelle stesse condizioni di Maurizio...
log23 - log35 ?
prima possibilità:
1/log3(2) - log35
(1 - log35 log32)/log32 ?
> 1 < 1
oppure
log23 - log25/log23
(log23 log23 - log25)/log23 ?
> 1 >1 >1
Restando sul grafico che ho pubblicato prima, ora l'ho elaborato con geogebra per un maggiore dettaglio. Il grafico fatto a mano per punti, approssimando quindi le due curve a due spezzate, non può dimostrare in modo assoluto che il log base 2 di 3 è maggiore del log base 3 di 5. Faccio riferimento al seguente nuovo grafico:
Restando sui segmenti di retta che approssimano le curve, si vede che per y=5 ottengo il punto E la cui ascissa è il punto blu sull'asse delle x. Per y=3 ottengo il punto F la cui ascissa è il punto rosso sull'asse delle x. Il punto rosso ha ascissa maggiore del punto blu, quindi sarebbe dimostrato che il log base 2 di 3 è > del log base 3 di 5. Ma se dalla spezzata passo alle curve cosa succede ? Non posso saperlo, non potendo utilizzare i grafici delle curve elaborati da geogebra (il quiz diceva che è sufficiente la sola definizione del logartimo e tanta fantasia..).
Allora ragiono così. L'ascissa del punto F (ottenuto partendo da y=3) è sicuramente 3/2. Lo si deduce da facili considerazioni geometriche. Con tale ascissa, mi sposto ora sulla curva blu (y=3 ^ x). Avrei quindi 3^(3/2) cioè radq(3^3) = radq(27). Non posso usare calcolatrici ma facendo conti a mente trovo facilmente che la radice quadrata di 27 è qualcosa di più di 5, comunque >5. Il punto H, quindi, sarebbe a ordinata maggiore del punto L (ottenuto partendo da y=5). Ciò significa che l'ascissa del punto L, essendo la curva crescente per x crescente, è minore dell'ascissa del punto H, quindi anche di quella del punto F sulla spezzata relativa alla curva rossa. Allora, dalla figura ora si vede subito che l'ascissa del punto N, ottenuto partendo da y=3 fino ad intercettare la curva rossa, sarà sicuramente maggiore di quella del punto F, quindi di quella del punto H e di quella del punto L. In altre parole, log base 2 di 3 > log base 3 di 5
mi piace e ci siamo quasi però si può semplificare ulteriormente, dimenticandosi completamente del grafico. Lo stesso ragionamento fatto per 27..si può estendere. Possiamo confrontare i due logaritmi che sono dei numeri irrazionali con dei numeri razionali
mettiamola così...
Se disegno la curva y=2x, posso ricavare il valore di x (x1)tale che y = 3 e analogamente il valore di x (x2) tale che y = 5. E poi confrontare i risultati... ma la considero soluzione grafica...
log23 log23 - log25
log23 log23 - log26 log26 > log25
log23 log23 - log2(3 x 2)
log23 log23 - (log2 3 +1) x =log23
x2 - x - 1 deve essere più grande di (1+(5)1/2 )/2 circa 1.5
log23 log23 - log2(2 x 2) log24 < log25
x2 - 2 deve essere più grande di 1
Si possono fare stime, ma non vedo una soluzione analitica precisa... si vede che ho compiuto 73 anni. Sono proprio andato.... largo ai giovani!!!!
La radice quadrata di 2 al cubo è minore di 3
La radice quadrata di 3 al cubo è maggiore di 5
Per ottenere 3 devo aumentare l'esponente di 2
Per ottenere 5 devo diminuire l'esponente di 3
Quindi il log2(3) è maggiore del log3(5).
Scusa Leandro ho rivisto l ultima parte con calma ma non si capisce nella conclusione. Manca qualcosa? O vuoi riscriverla meglio?
ancora un piccolo sforzo Maurizio; voglio solo vedere il tutto formalizzato così capiscono tutti.É il linguaggio della matematica.
Premessa: 1<log2(3)<2 1<log3(5)<2
Ipotesi: i due logaritmi sono uguali e valgono 1,5
Verifica: 2^(1,5) <3 3^(1,5) > 5
Conclusione: i due logaritmi sono diversi. Per ottenere 3 occorre un esponente > 1,5 e per ottenere 5 occorre un esponente <1,5. Quindi la risposta è log2(3) > log3(5)
sì, sì, ma bisogna fare dei calcoli... mi aspettavo una soluzione rigorosa... solo basata sulle proprietà...
ad esempio, io, su un'isola deserta non so che per ottenere 3 ci vuole un esponente maggiore di 1.5... e idem per 5. Se no... mica finivo in un'isola deserta!!!
E' vero;la dimostrazione di Maurizio non è ancora completa; deve basarsi su una catena di disuguaglianze e sulla definizione di logaritmo. Cominciamo a confrontare 5 con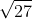
per esempio, usando le proprietà delle potenze.. non posso dire altro altrimenti tanto vale che scriva tutto.
chiaramente i discorso dell'isola si riferisce alla calcolatrice, oppure al computer e alle tavole logartimiche;
ciò che si sa per chi ha frequentato almeno la terza superiore è un altra cosa. escludiamo solo calcoli complessi con i decimali, o disegni computerizzati di funzioni. Per dirla ancora meglio: abbiamo a disposizione solo un foglio di carta e una matita. Comunque i conti di questo quiz si possono fare tranquillamente a mente.
Quindi la soluzione proposta in termini di logaritmi si potrebbe scrivere:
Complimenti a chi c'è arrivato!
ottimo Fabrizio!!!
Esattamente Fabrizio, poi vi racconterò la storia di questo quesito, pur rischiando la decapitazione.