Categorie: Meccanica Celeste Quiz
Tags: dinamica planetaria materia oscura moto circolare uniforme quiz
Scritto da: Vincenzo Zappalà
Commenti:60
Quiz: La catastrofe finale? */****
Questo quiz merita il racconto dell’antefatto e poi ognuno può affrontarlo come vuole…
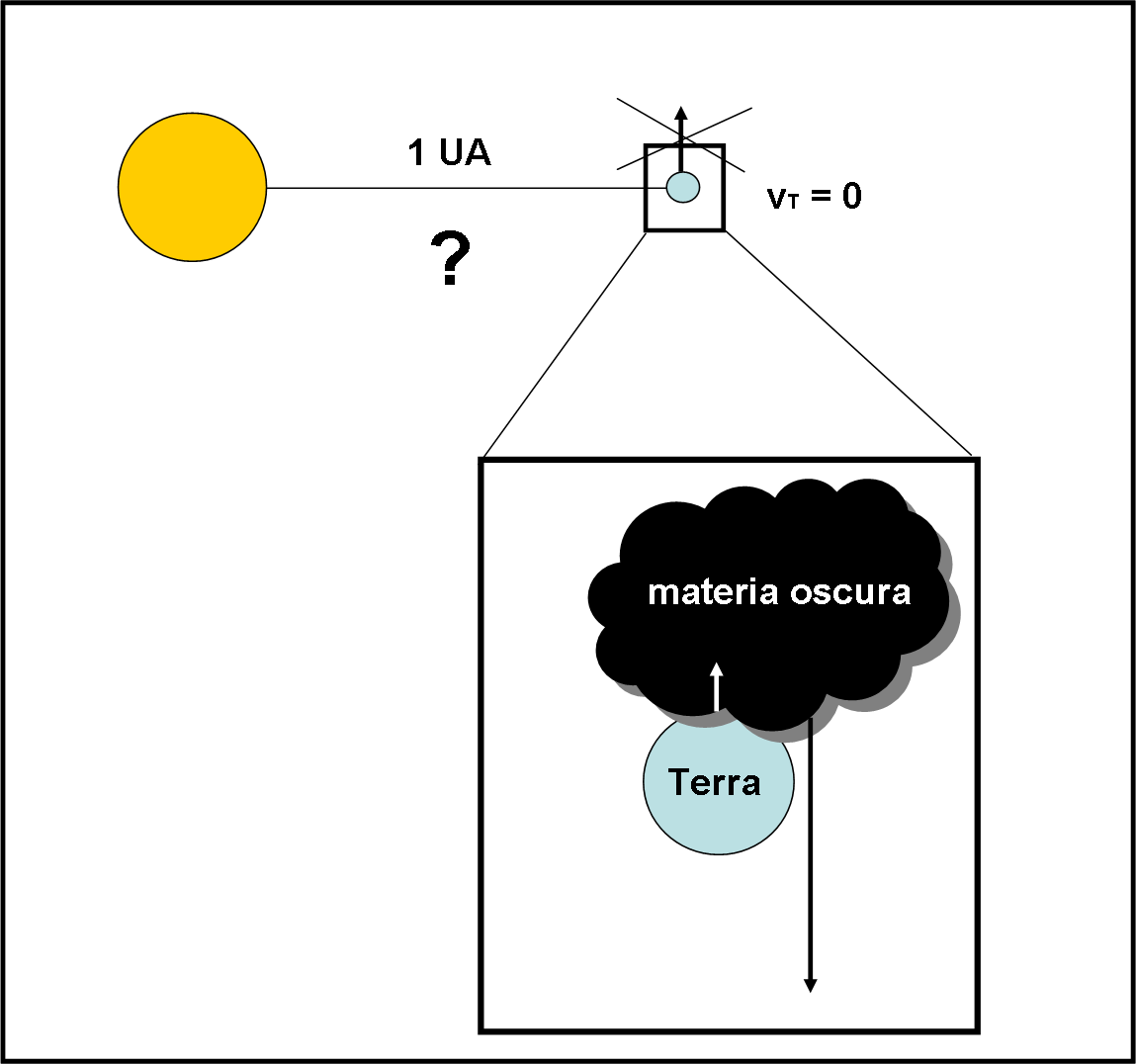
Un brutto giorno la Terra (e i suoi scienziati) fecero finalmente conoscenza della materia oscura. Conoscenza diretta, però, non attraverso osservazioni remote o esperimenti di laboratorio. Il nostro pianeta venne investito da una nube di materia oscura in moto rapidissimo, di cui nessuno si accorse visivamente ma che comportò un problema di una certa importanza: nel giro di pochi secondi la velocità orbitale della Terra si azzerò. Il nostro pianeta divenne un corpo di una certa massa (sempre la stessa) assolutamente FERMO nel sistema di riferimento eliocentrico.
Le domande che si fecero i terrestri furono molto semplici… “Che fine farà il nostro pianeta? E, soprattutto, avremo tempo di fare dei calcoli adeguati allo scopo?”
Vi sono vari modi per rispondere alle due domande (non certo per scongiurare la conclusione finale), sicuramente abbastanza impegnativi. Quindi, datevi da fare con forze, momenti angolari, energie e le loro varie conservazioni, ma non trascurate … l’asterisco isolato.
Considerate l’orbita della Terra perfettamente circolare e di raggio uguale a 1 Unità Astronomica, trascurando completamente la presenza della Luna. Inoltre, pensiamo solo al destino dinamico e non fisico...
Vinca il migliore…
60 commenti
difficile... eh?!
ti dirò che non mi é molto chiaro il problema.Non so come la materia oscura possa fermare in pianeta o se è importante saperlo. In ogni caso dopo tale materia lascia libera la terra di muoversi? Dobbiamo preoccuparci degli effetti di inerzia su quanto é legato alla terra al momento della fermata? Oppure di quelli che avvengono dopo quando la terra va in caduta libera sul sole, in un moto ad accelerazione fra l altro variabile?Non so se le mie domande siano lecite.
Caro Enzo, per ora pensavo di fornire una risposta da 1 asterisco.
Se la Velocità tangenziale della Terra diventa uguale a zero, non c’è più nulla che “bilancia” l’attrazione gravitazionale, per cui la Terra finisce dritta, dritta verso il Sole.
Il tempo impiegato per finire inglobata dal Sole dovrebbe dipendere essenzialmente dall’acellerazione di gravità, che però cambia continuamente.
Infatti, la Forza di gravità è uguale a:
F = G m(t) m(s)/r²
La forza esercitata sulla terra è uguale a:
F = m(t) a
Per cui, l’accelerazione è pari a:
a = F/m(t)
a = G m(t) m(s)/r² m(t) = G m(s)/r²
Il problema è che il raggio (ossia la distanza Sole Terra) cambia continuamente nel tempo, man mano che la Terra si avvicina al Sole.
Per ora preferisco fermarmi qui e pensarci (tra momenti di una Forza, conservazione del momento angolare, conservazione dell’energia, ecc.).
Paolo
La terra dovrebbe cadere in caduta libera verso il sole.
In una situazione ideale, con il sole attraversabile senza grande attrito, la terra dovrebbe iniziare ad oscillare tra il punto dove si trova ed il punto diametralmente opposto.
e vero Fabrizio, ma non so se la terra possa passare attraverso il sole, penso venga distrutta. Però mi viene in mente che forse la terra non cade verso il sole, ma lungo la congiungente del centro di massa del sistema solare, che non coincide con il sole. Dopo di Che potrebbe tornate in un orbita ma non so se ellittica o iperbolica
caro Umberto,
ovviamente la materia oscura è solo un espediente più o meno sensato per fermare il moto terrestre
cari tutti,
A noi interessa solo cosa succede da quel momento in poi...
Sulla prima domanda sembra che tutti siano d'accordo: dritta verso il Sole. Se la velocità s'annulla, la Terra si deve fermare (quantità di moto = 0) rispetto al Sole. Trascurando gli altri pianeti, l'unica forza che subisce è quella di gravità... e, praticamente, il Sole non si sposta di niente, dato l'impari confronto. Fin qui il solo asterisco ci sta tutto, ovviamente.
Il bello è però che la seconda domanda parla di tempo sufficiente a fare certi calcoli. I calcoli sono proprio quelli necessari a stabilire quanto tempo rimane alla Terra prima di una catastrofe apparentemente inevitabile: finire sul Sole è cosa ben poco piacevole...
A noi interessa solo la parte dinamica... sugli effetti fisici (temperatura, marea, ci potremo tornare dopo).
I quattro asterischi vanno proprio a fagiolo per quei calcoli dinamici (accelerazione e distanza variabili) che portano all'equazione del moto e, alla fine, al tempo impiegato a cadere...
Posso solo ricordare che l'energia iniziale è solo potenziale. Poi, però...
Insomma fate voi... metodi ce ne sono almeno due...
Ricordatevi, però, che l'asterisco isolato potrebbe ancora servire...E' difficile trovare la soluzione sul web, ma, dato l'interesse del quesito, invito tutti caldamente a non andare a cercarla... (me ne accorgerei sicuramente per più di un motivo...)
A occhio va bene così ma il Professore è sottile ma non banale. Il viriale impone che il doppio della cinetica sia uguale all'energia potenziale. Questo vale sempre. se la terra si ferma la sua cinetica va a zero e quindi si ha una situazione di energia potenziale uguale a -Mm/R (R è il raggio dell'orbita). Tale energia potenziale deve trasformarsi in energia cinetica man mano che la terra viene attirata dal sole.
Il problema è che viene fuori un'equazione differenziale del secondo ordine e di secondo grado che io personalmente non so risolvere.
Però possiamo dire che la velocità finale (all'arrivo sul sole di diametro tracurabile rispetto al raggio dell'orbita 700mila Km contro 150 milioni di Km) è
Poiché la massa della terra accelera progressivamente la sua velocità sarà sempre inferiore di una legge lineare descritta dalla retta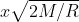
ove x è la distanza istantanea dal sole e R il raggio dell (ex) orbita.
La soluzione dell'equazione semplificata dello spazio percorso nel tempo è
quindi il tempo di approccio è inferiore a
Tenendo conto che la massa del sole è circa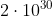
Kg e il raggio dell'orbita 150 10^9 m
svolgendo i calcoli si ottiene un tempo di circa 15 secondi. Un po' pochini per fare questi calcoli.
Scusate l'errore di sbaglio , mi son dimenticato di calvcolare il logaritmo. Il risulato finale è 386 secondi, cioè più di 6 minuti. Considerando che il movimento come abbiamo detto è sicuramente più lento, penso invece che un buon fisico potrebbe farcela a calcolare il tempo di impatto.
Leandro, come sempre, non si spaventa, ma... il suo tempo proposto è molto lontano dal vero...
Comunque, se vi trovaste di fronte a integrali particolarmente complicati (dico "se"...) è ammesso il loro calcolo attraverso alcune risorse esistenti in rete...
Intanto cominciamo a stendere per bene la problematica e a descrivere le equazioni utili allo scopo...
Ricordo ancora, però, che anche i meno esperti possono comunque TENTARE di arrivare in fondo...
E' ammesso un errore del 5% (a parte le semplificazioni imposte al problema che esistono per qualsiasi approccio).
FORZA quindi... senza paura o timore reverenziale... Newton ce l'avrebbe fatta!
Una scorciatoiveloce:
la luce impiega 8 minuti per coprire la distanza, quindi il tempo di percorrenza della terra deve per forza essere molto superiore, quindi sufficiente.
Parto dall'ipotesi ideale che ho detto sopra. Averi un'orbita ideale degenere.
E se valesse anche per questo caso la terza legge di Keplero?
Poiché r e K sarebbero gli stessi di quelli della Terra che gira, anche questo T ideale sarebbe lo stesso. Cioè sarebbe il nostro anno di 365 gg.
La caduta corrisponde ad 1/4 dell'orbita e quindi avrei un tempo di caduta di circa 3 mesi.
Il dubbio è che valga ancora la terza legge di Keplero per questo caso degenere.
da questo momento in poi non dico più niente... il gioco è bello perché è vario... (Leandro... voglio un valore abbastanza buono del tempo...
)
SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSHHHHHHHHHHHHHHHHHH !!!!! (Silenzio totale)
Il problema di caduta di un grave in condizioni di accelerazione di gravità non costante è però un problema differenziale-integrale di cui conosco la soluzione,nota in letteratura,anche se non molto famosa,che riguarda fra l'altro un oggetto particolare già visto altre volte nei quiz. Quindi non posso rispondere.
OK Umberto... grazie
caro Umberto,
dato che io penso di spiegare solo la soluzione "semplice", tu potresti (se ne hai voglia) scrivere quella più complessa... sempre che non ci arrivi prima qualcun altro... Che ne dici?
La accelerazione gravitazionale sulla superficie del sole vale&space;=&space;GM/r^2)
Dove G è la costante di gravitazione universale, M la massa del sole e r il suo raggio.
Se questo valore fosse costante a qualsiasi distanza, la terra cadrebbe dalla distanza "d" , sul sole, in un tempo t =)})
= 
= 33.210 secondi.
Quindi il tempo disponibile sarebbe di 9 ore e 13 minuti.
Naturalmente il tempo di caduta è maggiore perché alla distanza di 150 milioni di chilometri l' attrazione iniziale del sole è ridotta, in ragione del quadrato della distanza, a un valore iniziale insignificante, circa 46.000 volte più piccola di quella al suolo.
In ogni caso, avendo a disposizione ben più di 9 ore, il tempo di fare i conti ci dovrebbe essere.
Con una simulazione ad intervalli di 10 secondi si ottiene un tempo di caduta di 26 giorni e 15 ore
Per ottenere il dato preciso occorre risolvere l'equazione differenziale non lineare di secondo ordine che lega l'accelerazione all'inverso del quadrato della distanza.
mi aspetto molto di meglio da te... Mau.
Ripeto: il tempo c'è... d'accordo, ma quanto vale esattamente o quasi?
Ci sono però passaggi e trucchetti difficili, non so . Bisognerebbe semplificarla . Comunque aspettiamo, e vediamo se qualcuno riesce a fare qualcosa di comprensibile.
Ok Umberto, aspettiamo e vediamo...
Ecco...aspettate.
dai Mau... tu puoi farlo (e non sei il solo... acci... non posso dire di più, ma...)
Io ho fatto una prova per approssimazioni successive... alla fine ottengo un tempo pari a circa 504 giorni affinché la Terra raggiunga la superficie del Sole...
Devo però controllare bene i calcoli che ho fatto.
Paolo
Il metodo che ho usato per stimare il tempo necessario alla Terra per raggiungere il Sole è il seguente.
Dato che l’accelerazione di gravità è uguale a:
a = GM/r²
Dove
G è la costante di gravitazione universale = 6,67 x 10^-11 m³/Kg s²
M la massa del Sole = 1,9885 x 10^30 Kg
e r la distanza Sole Terra (che varia continuamente)
Per ricavare il tempo, uso la relazione:
S = ½ a t²
t² = 2S/a
t = √2S/a
A questo punto, partendo da una distanza Terra-Sole di 150 milioni di km (150 miliardi di metri) uso intervalli di spazio (S) pari a 1 milione di Km, o meglio 1 miliardo di metri.
Calcolo l’accelerazione di gravità alla distanza di 150 milioni di Km (0,00589 m/s²), dopodiché calcolo il tempo per percorrere 1 milione di Km con quell’accelerazione (582479 secondi).
Ora la Terra si trova a 149 milioni di Km dal Sole, ricalcolo l’accelerazione di gravità a quella distanza e poi trovo il tempo impiegato per avvicinarsi di un altro milione di km al Sole e così via.
Alla fine, quando la Terra raggiunge la superficie del Sole (0,6960 x 10^9 metri), sommo tutti gli intervalli di tempo trovati ed ottengo 43 578 276 secondi, pari a circa 504 giorni.
Paolo
Accidenti ho toppato alla grande!
Così la Terra ogni volta si ferma e poi riparte, mentre man mano che accelera acquista una velocità di cui occorre tener conto, ossia:
S = ½ a t²+ v t
Tocca rivedere tutto!
Paolo
Caro Paolo, io ho impostato la simulazione ricalcolando accelerazione, velocità e posizione ogni 10 secondi e ho ottenuto un tempo totale di meno di 4 settimane, che ritengo troppo grande.
In base al bilancio delle energie potenziale e cinetica mi verrebbe una velocità finale di 616 Km/s . In quel momento l'accelerazione è 274 m/s^2 e la posizione è 700.000 Km dal centro del Sole.
L'ultima riga della simulazione dovrebbe approssimare tutti e tre questi valori. Solo in quel caso la somma dei tempi sarebbe vicina a quella precisa.
o affrontate l'equazione differenziale o dovete cambiare percorso... consiglio da amico...
anche se qualcosa di buono è stato detto, tra le righe...
non posso dire di più perché diventerebbe troppo facile, almeno per uno di voi ...
La velocità finale ha lo stesso valore della velocità di fuga.
Il tempo per scappare dal sole e arrivare a 150 milioni di km è lo stesso che passa cadendo sul sole ( con velocità iniziale nulla) da quella distanza
Non è che impiega un quarto di 365, 5 giorni , come dice Fabrizio , eh..?
La 3a legge di keplero vale solo se le orbite sono circolari (più o meno), infatti deve essere presente una forza centrifuga che in questo caso non c'è.
Leandro , credo che la terza legge di Keplero sia applicabile in generale a orbite ellittiche, anche se le orbite di molto pianeti sono quasi circolari.
Ripensando all'idea di Fabrizio, si può dire che, nel momento di inizio della sua caduta, la Terra si avvia lungo il segmento che la congiunge al Sole, come se si muovesse su una ellisse degenere, in cui il Sole occupa il fuoco all'estremo opposto del segmento-ellisse, alla distanza di 150 milioni di km. Insomma, per la Terra, la bella orbita quasi circolare su cui ha rotolato per 4 miliardi di anni e mezzo, è solo un ricordo.
Il semiasse minore " b" di questa nuova "orbita" ( si fa per dire) è nullo e il semiasse maggiore "a" misura 75 milioni di km.
La distanza percorsa nella caduta è quindi il doppio del semiasse maggiore ed il tempo impiegato è la metà del periodo di rivoluzione P lungo questo segmento-ellisse.
Ora, sappiamo, dalla terza legge di Keplero, che il quadrato del periodo di rivoluzione (P) è proporzionale al cubo della distanza media dalla massa attrattiva (Sole) , distanza media che è proprio il semiasse maggiore (a).
La costante di proporzionalità è determinata dalla legge di gravitazione di Newton e vale:
In definitiva la relazione, di cui si trova una dimostrazione qui , è la seguente:
da essa posso ricavare il periodo di rivoluzione P
il tempo di caduta che cerchiamo è metà di questo periodo.
tempo caduta =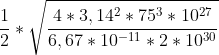
=
=
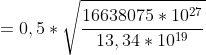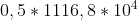Si tratta comunque di un valore approssimato, rispetto a quello rigoroso ottenibile integrando l'equazione differenziale , non lineare , di secondo ordine , cosa che richiede alcuni accorgimenti ed artifici come accennava appropriatamente Umberto, probabilmente riconducendo l'equazione di secondo ordine ad una equazione non lineare di primo ordine.
Una buona notizia per i "simulatori".... Dopo avere ripulito alcuni errori presenti nella precedente simulazione, vi propongo in questa figura le
ultime righe della simulazione corretta della caduta sul Sole con intervalli di calcolo di 100 secondi.
Dopo oltre 55.800 iterazioni si hanno questi valori.
Da notare la concomitanza dei risultati:
ci troviamo (quasi) sulla superficie del Sole, a 743.000 Km dal suo centro.
sono stati percorsi in caduta libera 149,317 milioni di Km
l'accelerazione , alla quota di circa 50.000 km dalla superficie del sole è 241 m/s^2
la velocità "finale" alla stessa quota è 612,4 km/s
la durata totale della caduta è di 5.586.110 secondi, pari a 64 giorni e 15 ore.
Una notevole convergenza di risultati rispetto a quelli del commento precedente.
Ora sarebbe interessante poter vedere i risultati della integrazione della equazione differenziale ...
Provo a seguire alcuni suggerimenti di Enzo. Non trovo il modo di cambiare percorso, affronto quindi l'equazione differenziale.
Enzo ha sottolineato anche che l'energia iniziale, quella che si conserva, è tutta energia potenziale:
Nella caduta appare anche l'energia cinetica K,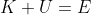
che espansa diventa
Mi accontento di questa approssimazione che trascura l'energia cinetica del sole poiché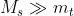
.
Dalla relazione trovata ricavo v.
Ci vuole un piccolo trucco, che ho visto spesso applicato dei testi di fisica, e qualche buona tabella di integrali o qualche aiuto informatico (Enzo li aveva ammessi in uno dei primi commenti).
L'obiettivo che abbiamo è quello di trovare il tempo di caduta. Ci servirebbe avere una relazione del tipo t funzione di r,)
per poi calcolare il tempo che deve trascorrere per andare dal punto iniziale sull'orbita terrestre fino al sole: -t(R_t))
. L'equazione sopra invece sembra contenere una r funzione di t, c'è anche una derivata di r rispetto a t. Qui c'è il trucco che dicevo. Una capriola della relazione che facciamo diventare:
Qui per risolvere l'integrale occorre ricorrere alle tabelle o ad altri strumenti.
Il risultato per l'integrale indefinito&space;-\sqrt{&space;R_t-r}&space;\,\sqrt{r})
.
Calcolato nei due estremi di integrazione è: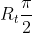
per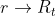 
e 0 per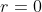 
Quindi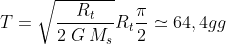
Il risultato è diverso da quello ottenuto applicando la 3a legge di Keplero. La differenza è un fattore di circa
.
Se l'errore sia nel tentare di applicare la 3a legge di Keplero a questo caso o sia in questo ragionamento o sia in tutte e due non lo so.
Caro Fabrizio, prima di tutto i miei complimenti per avere affrontato l'integrazione, su cui mi stavo accanendo inutilmente prima di vedere il tuo post.
Mi sembra che il tuo risultato sia molto vicino a quello che appare nei miei due commenti precedenti che forse non hai visto. Questo valore di 64, 4 giorni trova riscontro sia nel calcolo con Keplero, sia con i risultati della simulazione. A questo punto , se siamo in democrazia, ci sono a disposizione più di due mesi per fare un calcolo che ci ha impegnato un paio di giorni.
Bene, ragazzi, molto bene!
Innanzitutto i più vivi complimenti a Fabrizio, non solo per aver affrontato l'equazione differenziale, ma -soprattutto- per avere avuto l'idea "luminosa" iniziale: terza legge di Keplero!
L'energia orbitale dipende solo e soltanto dal semiasse e non dall'eccentricità, per cui l'orbita può essere stretta quanto si vuole, ma il periodo non cambia. Addirittura si può considerare il caso degenere dell'ellisse rettilinea,in cui si considera e = 1, ma senza cadere nella parabola. Comunque, non vale la pena di andare per il sottile... può bastare considerare META' dell'orbita "nuova", ossia metà del periodo orbitale in cui il semiasse DEVE coincidere con la metà della distanza Terra Sole. L'errore commesso da Fabry, era di mantenere l'orbita iniziale con a = 1 UA, cosa assurda dato che l'energia totale era cambiata...
In realtà, non c'è bisogno di ricordare tante costanti...
P2 = a3 per le distanze in UA e il periodo in anni... ossia:
P = a3/2 = √1/8
P/2 = 1/(2√8) ∼ 0.177 = 64.5 giorni
in ottimo accordo con quanto trovato per via analitica...
Grazie Fabrizio per avermi salvato da un lavoraccio.. quell'integrale si calcola ma sono talmente tanti gli Artifizi e i cambi di variabile che tanto vale affidarsi ad una tabella. D'altronde tale risoluzione tecnica non avrebbe valore educativo.
Caro Maurizio, la tua applicazione della terza legge di Keplero a questo caso da un risultato diverso da quello che pensavo. Forse hai ragione tu, data la coincidenza dei risultati numerici, ma dico perché mi aspetterei circa 90gg. 1/4 del periodo di una orbita di semiasse maggiore pari al raggio dell'orbita terrestre.
La nostra orbita ideale degenere dovrebbe avere come semiasse maggiore il raggio dell'orbita terrestre. Supponiamo idealmente che il sole sia attraversabile senza attrito. La terra partendo da ferma a distanza Rt (massima energia potenziale) cadrebbe verso il sole. All'attraversamento del sole avrebbe la massima energia cinetica. Con questa energia cinetica proseguirebbe fino a raggiungere un punto a distanza Rt dal sole simmetricamente opposto al punto di partenza (energia cinetica nulla e massima energia potenziale). Da questo punto tornerebbe indietro facendo lo stesso percorso a velocità opposte a quelle dell'andata fino a ritornare al punto di partenza. È così via, una specie di pendolo. Il semiasse maggiore di questo percorso è di lunghezza Rt e l'impatto fermerebbe la terra ad 1/4 del percorso.
La terza legge di Keplero, se applicabile, fa dipendere il periodo dal semiasse maggiore dell'orbita che è sempre Rt. Quindi mi aspetterei un periodo di 365gg. L'impatto dovrebbe essere a 365/4 gg.
Scusate, ho risposto a Maurizio senza vedere che nel frattempo erano arrivati altri commenti.
Comunque la risposta illustra la fonte dell'errore che ho fatto nell'applicazione delle terza legge di Keplero.
L'errore c'è, ma francamente non ho ancora capito dove sia.
caro Fabry,
nel caso iniziale tu ammetti che l'energia del sistema rimanga la stessa, ma così non è perché hai eliminato l'energia cinetica dovuta alla velocità orbitale. ne segue che il semiasse deve cambiare...
Attenzione anche alla velocità finale... quanto vale per r = 0 ?
Ho riprovato a fare una simulazione, ottenendo come risultato 65,6 giorni.
Il metodo usato è il seguente.
Innanzitutto ho utilizzato l’Energia cinetica in rapporto a quella di potenziale per calcolare tutte le velocità della Terra a intervalli di 1 milione di Km per volta.
Energia iniziale = - GMm/ri
Dove ri è la distanza iniziale di 150 milioni di Km.
Tale Energia deve conservarsi, pertanto:
- GMm/ri = ½ mv² - - GMm/rn
Dove rn è la distanza Sole Terra, mentre la Terra si avvicina al Sole.
- GMm/ri + GMm/rn = ½ mv²
- 2GM/ri + 2GM/rn = v²
- 2GM rn + 2GM ri /(ri rn ) = v²
2GM (- rn + ri)/(ri rn )= v²
V = √ 2GM (ri - rn)/(ri rn )
Dopodiché, considerato che l’accelerazione di gravità è uguale a:
a = GM/r²
Calcolo l’accelerazione sempre a intervalli di 1 milione di Km.
a = GM/rn²
L’accelerazione, però, è anche uguale a:
a = ΔV/Δt
Δt = ΔV/a
A questo punto non resta che calcolare i tempi ogni milione di Km, dato che ho tutte le velocità che servono per ogni tratto di 1 milione di Km (ΔV = V – V precedente) e uso per approssimazione l’accelerazione calcolata a inizio del tratto di 1 milione di Km preso in considerazione.
In ultimo sommo tutti gli intervalli di tempo calcolati fino al raggiungimento della superficie del Sole ottenendo 5 674 077 secondi, pari a circa 65,6 giorni.
Il risultato si avvicina abbastanza a quello corretto e l’errore è frutto delle approssimazioni (ho considerato l’accelerazione quasi costante nel vari tratti di 1 milione di Km, ma in realtà questa è solo un’approssimazione).
Paolo
in pratica sono stati usati tre metodi: quello immediato legato alla terza legge, quello rigoroso basato sulla conservazione dell'energia e quello ad approssimazioni successive. L'ultimo andrebbe benissimo utilizzando un computer facendo integrazioni numeriche... ma è quello che mi piace di meno...
caro Fabrizio,
mettiamola così (in modo estremamente semplificato):
Tu lavori stringendo l'orbita, ossia trasformando la circonferenza in una ellisse... Ma, facendo questo , il fuoco (ossia il Sole) non può rimanere al centro, ma si deve spostare sempre più verso l'estremo dell'orbita. Addirittura a una distanza dalla Terra pari a 2a, nel caso degenere. Ma, allora tu non calcoleresti il tempo di caduta rispetto al Sole attuale, ma rispetto a un Sole che si è spostato proprio di a rispetto alla posizione iniziale... Ne segue che l'orbita ellittica deve avere il Sole a una distanza sempre uguale a quella di partenza, ossia a una distanza pari ad a, che diventa il doppio del semiasse della nuova orbita (fuoco posto nella posizione opposta a quella della Terra nel momento iniziale).
caro Enzo, certamente è vero che l'energia totale cambia. Il dubbio è che, nonostante questo, non cambi l'asse maggiore. L'orbita degenere dovrebbe oscillare tra i due punti opposti di massima energia potenziale. Se il punto di partenza è a distanza dal sole pari al raggio dell'orbita terrestre, Rt, allora dovrebbe oscillare tra Rt e -Rt. Il semi asse maggiore degenere sarebbe ancora Rt. Non ho capito come diventi Rt/2. Mi sfugge qualcosa.
D'altra parte orbite ellittiche di questo tipo, se non sbaglio, dovrebbero avere energia diversa, ma stesso periodo. Continuando a ridurre l'asse minore si avrebbe come caso limite l'orbita degenere.
Il secondo punto che sollevi, cioè la presenza di una singolarità nel potenziale per r=0 dovuta alla semplificazione del modello, è la principale ragione per la quale dubitavo di poter applicare la legge di Keplero in questo caso.
Enzo, non avevo visto ancora il tuo ultimo commento. Avevo ignorato la posizione del fuoco. Mi rimane ancora il dubbio sulla oscillazione tra Rt e -Rt. Ci penso.
No, Fabrizio... la figura precedente mostra orbite che hanno tutte la stessa energia: l'energia dipende solo dal semiasse e non dall'eccentricità. Anche il periodo rimane costante, dato che anch'esso dipende solo dal semiasse...
L'errore è sempre dovuto al non avere considerato la posizione del fuoco, diversa in ciascuna delle orbite.
Avevo pensato che l'energia potenziale fosse la stessa per tutte queste orbite all'afelio. Invece no.
OK... comunque complimenti per l'idea che era "quasi" perfetta! Nella soluzione, includerei la tua determinazione rigorosa come appendice... che ne dici?
Come dire..è un onore!
nel affrontare il quiz ho notato Che alla fine di fisica ne serve ben poca. Se si sa la legge di gravitazione e la definizione di accelerazione si può deducurre tutto matematicamente dagli integrali. Quindi mi ero un po' dannato a risolvere anche l integrale più difficile, non l ho trascritto in latex ma se serve posso farlo. Purtroppo con la mia fissazione matematica bisogna sempre dimostrare tutto.. Possiamo sempre essere in un isola deserta. Ma a parte questo volevo fare una domanda.. Visto che il moto non ha accelerazione costante, la legge oraria non può essere parabolica. Guardando l integrale che avevo elaborato in modo leggermente diverso mi sono accorto che assomigliava molto af una curva che abbiamo visto molte volte recentemente r sto cercando di dimostrarlo. Mi farete sapere se sapete già che curva e
Caro Umberto,
il moto dovrebbe essere rettilineo nel caso rigoroso (non vedo cosa possa fare muovere la Terra rispetto alla congiungente col Sole) e ellittico nel caso approssimato... o, se vuoi, rettilineo lungo un ellissi degenere (che non è una parabola, però). Nel secondo caso siamo noi che imponiamo un moto ellittico molto stretto, ma abbiamo poco interesse a descrivere il moto... basta conoscere il periodo.
Se, comunque, vuoi descrivere il tuo metodo vai pure avanti e faremo un'altra appendice... o, nel caso, faremo un tutt'uno con quello di Fabry.
Ops Umberto!
avevo letto male "legge oraria..." e avevo pensato alla traiettoria. Non mi dirai che viene fuori una cicloide????!!!!! No, non ho ancora pensato alla legge oraria...
per Fabry e Umberto,
se proprio volessimo fare i fini, bisognerebbe inserire anche il raggio della Terra e del Sole... ma direi che se ne può fare a meno....
Lo scopo del quiz è stato abbondantemente raggiunto sia attraverso l'impostazione dell'equazione differenziale, sia attraverso la semplice legge di Keplero. Poi, accettiamo pure l'approccio "da computer" di Mau e Paolino...
sembra proprio una cicloide!
e comunque si può dimostrare anche se è molto noioso.
Ieri sera ho guardato in faccia la curva dello spazio percorso in funzione del tempo, pensavo anche di pubblicare la figura, poi ho lasciato perdere. Comunque, se può servire, è questa...
Colgo l'occasione per ricordare che il mondo reale è ben più complesso della rappresentazione che ce ne facciamo con le nostre "leggi" scoperte tra conchiglie e ciottoli sulla spiaggia del grande oceano della conoscenza.
Le umili macchine che abbiamo costruito negli ultimi decenni per fare il lavoro sporco, ci hanno regalato il miracolo di poter vedere l'invisibile.
Senza di esse, senza i metodi di integrazione numerica, la natura elusiva del mondo ci sfuggirebbe completamente. Non avremmo telescopi spaziali e sonde che esplorano l'universo. Saremmo chiusi negli angusti limiti di conoscenze provinciali.
"È indegno per l'uomo eccellente perder tempo come uno schiavo nel lavoro di calcolare, cosa che potrebbe essere relegata senza problemi a qualcun altro se fosse usata una macchina."
Sono parole di Leibniz, pronunciate esattamente 360 anni fa. Sarebbe contento, lui, di sapere che quelle servizievoli macchine, figlie di un Dio minore, ora esistono e ci assistono.
io ho apprezzato molto il vostro approccio algoritmico.poi sai che sono un programmatore. Anche Hilbert la pensava come Leibnitz, ma era ancora più drastico.sperava di poter affidare lo sviluppo teorico della matematica ai computer. Il suo sogno però falli.
Ma io scherzo come sempre... d'altra parte ti voglio vedere a far girare qualche asteroide per cento milioni di anni senza algoritmi del genere...
Ah... l'ho fatto anch'io, lo fatto anch'io... 
Tra parentesi questa è la figura che viene fuori facendo qualche calcolo meno approssimato (distanza e tempo sono normalizzati alla distanza totale e al periodo)