QUI la domanda del quiz

Risolto il piccolo inghippo sull’ombra mattutina e serotina (oltre il circolo polare), il tutto si risolve con poche relazioni tra angoli o ricordando i sistemi di coordinate celesti.

L’importante è scegliere il sistema di riferimento (QUI).

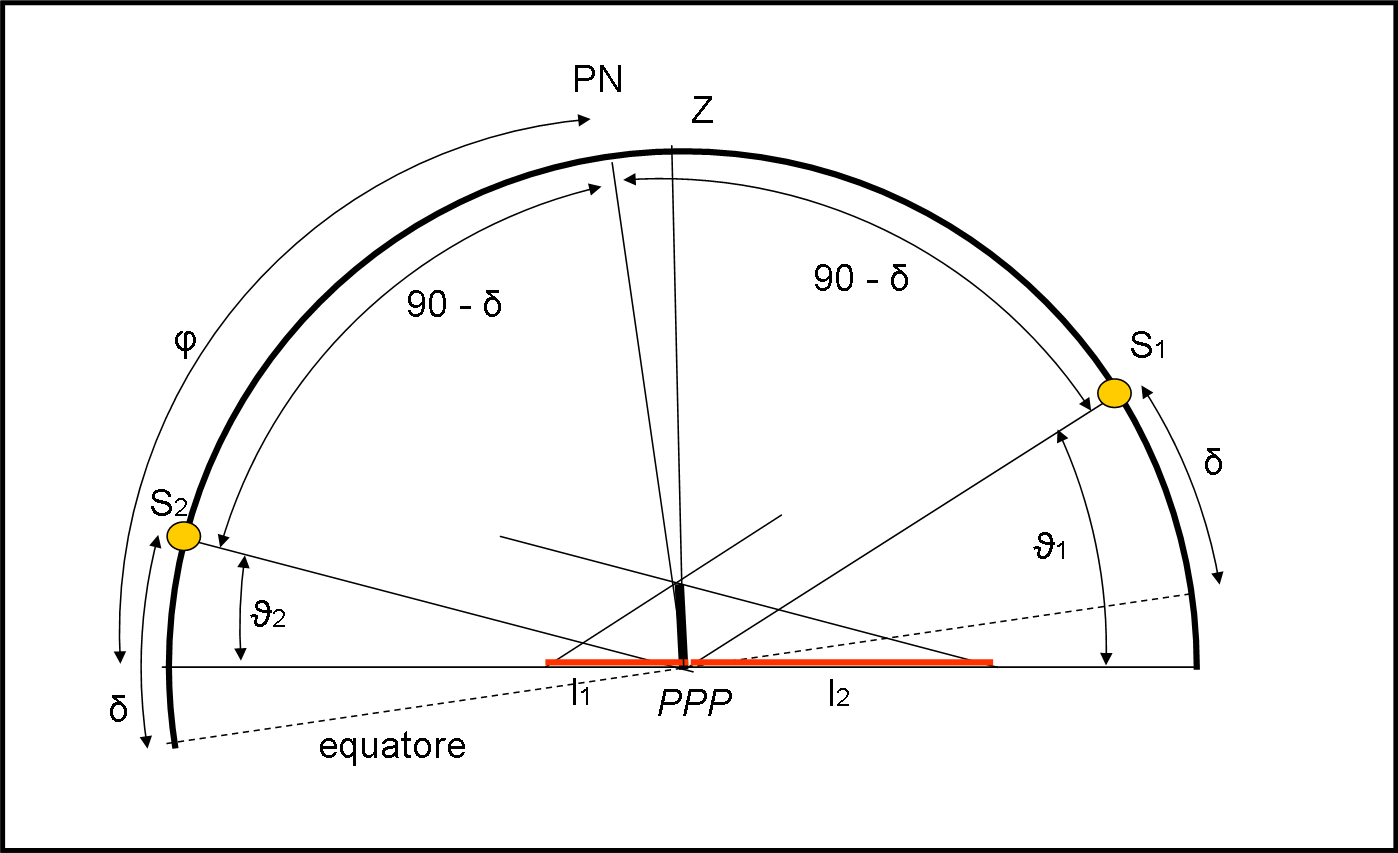
Maurizio ha considerato un sistema geocentrico eclittico, mentre Leandro si è messo in un sistema geocentrico equatoriale, seguito da Andy… ma il discorso non cambia utilizzando un sistema centrato nel luogo (altoazimutale). Noi useremo quest’ultimo, come rappresentato nella Fig. 1, dove il cerchio massimo è il meridiano del luogo, la linea orizzontale l’orizzonte e il Sole viene indicato nel suo punto di massima e di minore altezza (la linea che li congiunge è, ovviamente, parallela all’equatore).

Nella figura sono indicati gli angoli fondamentali (φ, latitudine del luogo, e δ, declinazione del Sole) che vogliamo determinare. La prima cosa da fare, seguendo Eratostene e determinare gli angoli ϑ₁ e ϑ₂, ossia quelli che indicano la posizione del Sole rispetto all’orizzonte. Essi si risolvono utilizzando lo gnomone e misurando la lunghezza dell’ombra l (l’asta misura esattamente 1000 m = 1km):

tan ϑ₁ =  1/ l1 = 1/1.732

ϑ₁ = atan (1/1.732) = 30°

tan ϑ₂ =  1/l2 = 1/5.671

ϑ₂ = atan (1/5.671) = 10°

Determiniamo, adesso, attraverso la figura le relazioni tra ϑ₁, ϑ₂, φ e δ.

ϑ₁ = 180° – φ – (90° – δ) =  90° – (φ – δ) = 30°

φ – δ = 60°

ϑ₂ = φ – (90° – δ) = φ + δ – 90° = 10°

φ + δ = 100°

Il sistema

φ – δ = 60°

φ + δ = 100°

porta immediatamente alle soluzioni:

δ = 20°

φ = 80°

Freddino eh?! (malgrado il Global Warming…)

Ovviamente, il tutto poteva essere risolto applicando due volte la formula che lega l'altezza con la declinazione e la latitudine (passaggio dal primo al secondo sistema di riferimento):

sen  δ = sen φ cos z – cos φ sen z cos A

dove z è proprio ϑ e A... (siamo sul meridiano del luogo !). La formula sarebbe stata fondamentale se le misurazioni non fossero state fatte al meridiano (ossia alla massima e minima altezza del Sole).

Un po' di trigonometria sferica e di sistemi di coordinate celesti non fa mai male...