Ecco la soluzione (o meglio le soluzioni) al quiz "Diabolico" che trovate qui. La mia, che è di tipo geometrico-variazionale, non si discosta di molto da quelle di Vincenzo, Fabrizio, e dalle idee proposte da Mauro, Maurizio, Leandro. Diciamo che noi si siamo dannati un po' di più con i disegni, che sono però essenziali in questo  caso.

Diversa invece è la soluzione di Arturo, che si basa sul calcolo differenziale-integrale. Per me rimane la dimostrazione più rigorosa.

Propongo per prima la soluzione di Arturo:

Sia y=f(x) l'equazione della curva (generica).

Indico con a l'area a sinistra della retta blu e con b quella a destra. Indico con A il punto di intersezione della curva con la retta rossa inferiore e con B quello con la retta rossa superiore. Indico con P il punto di intersezione della curva con la retta blu. Siano  ,  , ,  le coordinate (considerate note) dei punti A e B. Siano x, y le coordinate , ignote, del punto P.

Ricordando il significato geometrico dell'integrale definito, posso scrivere:

Infatti, l'area a è la differenza tra l'area sottesa dalla curva tra A e P e il rettangolo avente base (x-) e altezza pari a

Stesso ragionamento per l'area b.

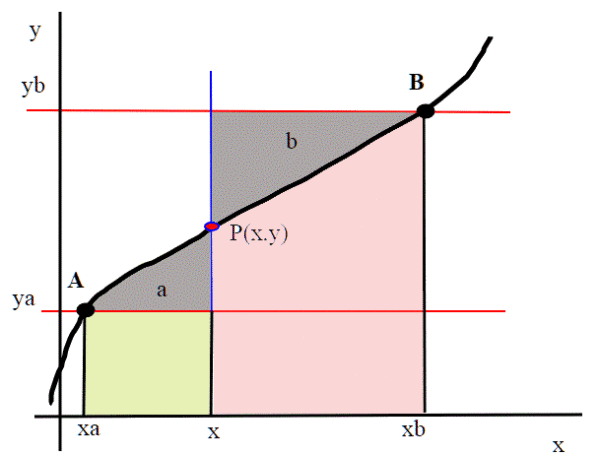
La somma delle aree , svolgendo i calcoli, è dunque data da:

cioè, mettendo in evidenza la x :

Poiché devo trovare il punto P per il quale si ha la minima somma delle aree, calcolo la derivata prima della suddetta espressione, ricordando il teorema fondamentale del calcolo integrale:

cioè:

Poiché tale derivata deve annullarsi, ottengo:

cioè:

Dunque, l'ordinata del punto P è a metà strada tra le due rette rosse.

 

La mia soluzione (Umberto)

Innanzitutto,  l'ordinata del punto cercato  deve stare per forza a metà della distanza fra le due linee rosse.

Non può star sopra:

la linea azzurra interseca la funzione sopra la linea di mezzeria. Può l'area formata essere minima?Immaginiamo di spostarci con la retta blue a sinistra, in modo che la nuova intersezione stia sempre sopra il punto di mezzeria(possiamo farlo grazie alla continuità).Chiamiamo L1, H1 i trapezoidi rosa e verde. L1  ha un area maggiore di H1,essendo la funzione crescente.  Ma allora l'area totale diminuisce di più di quanto sotto di quanto non cresca sopra. Quindi è più piccola, e l'area iniziale non è minima.

Non può star sotto:

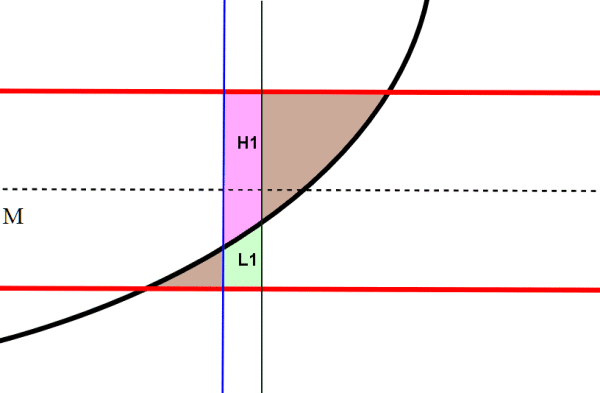
La linea azzurra interseca la funzione sotto la linea di mezzeria. Può l'area formata essere minima?Immaginiamo di spostarci con la retta blue a destra.  In questo caso (sempre per i motivi specificati sopra) S(H1)> S(L1),  Quindi  l'area diminuisce sopra di più di quanto aumenti sotto. Quindi è più piccola, e quella iniziale non è quindi minima.

Proviamo adesso che se la funzione interseca esattamente nella linea di mezzeria, allora l'area è minima.

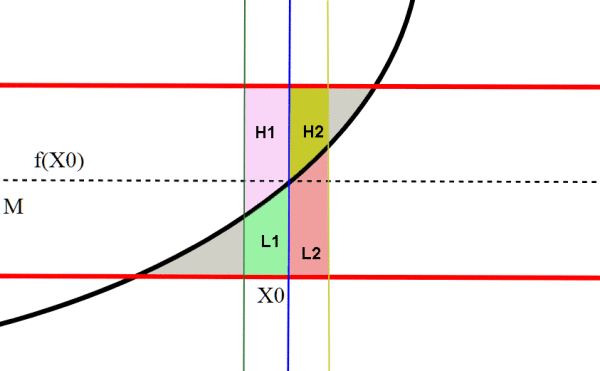
Se ci spostiamo verso destra, S(L2)>S(H2), quindi l'area sotto  aumenta più di quanto cali sopra. Se ci spostiamo a sinistra, S(L1)<S(H1). Quindi aumenta sopra più di quanto cali sotto. Sia destra che a sinistra l'area è maggiore per qualsiasi spostamento piccolo a piacere. Quindi X0 è un punto di minimo.

 

Soluzione di Vincenzo

Abbiamo a che fare con una funzione monotona crescente. Aggiungiamo poi che è anche continua, affinché non possano generarsi ambiguità, e ovunque definita.

La funzione può essere, perciò, una qualsiasi funzione y = f(x), definita in un certo intervallo e con certe caratteristiche.

Il risultato deve, quindi, essere UNICO per ogni f(x), altrimenti si chiederebbero soluzioni diverse per i vari tipi di f(x). Ne consegue che posso trovare il risultato per una funzione particolare e poi confermarlo per qualsiasi altra funzione.

L'approccio usato vuole essere puramente geometrico.

Come funzione particolare considero la retta che passa per i punti A e C (Vedi Fig. 1).

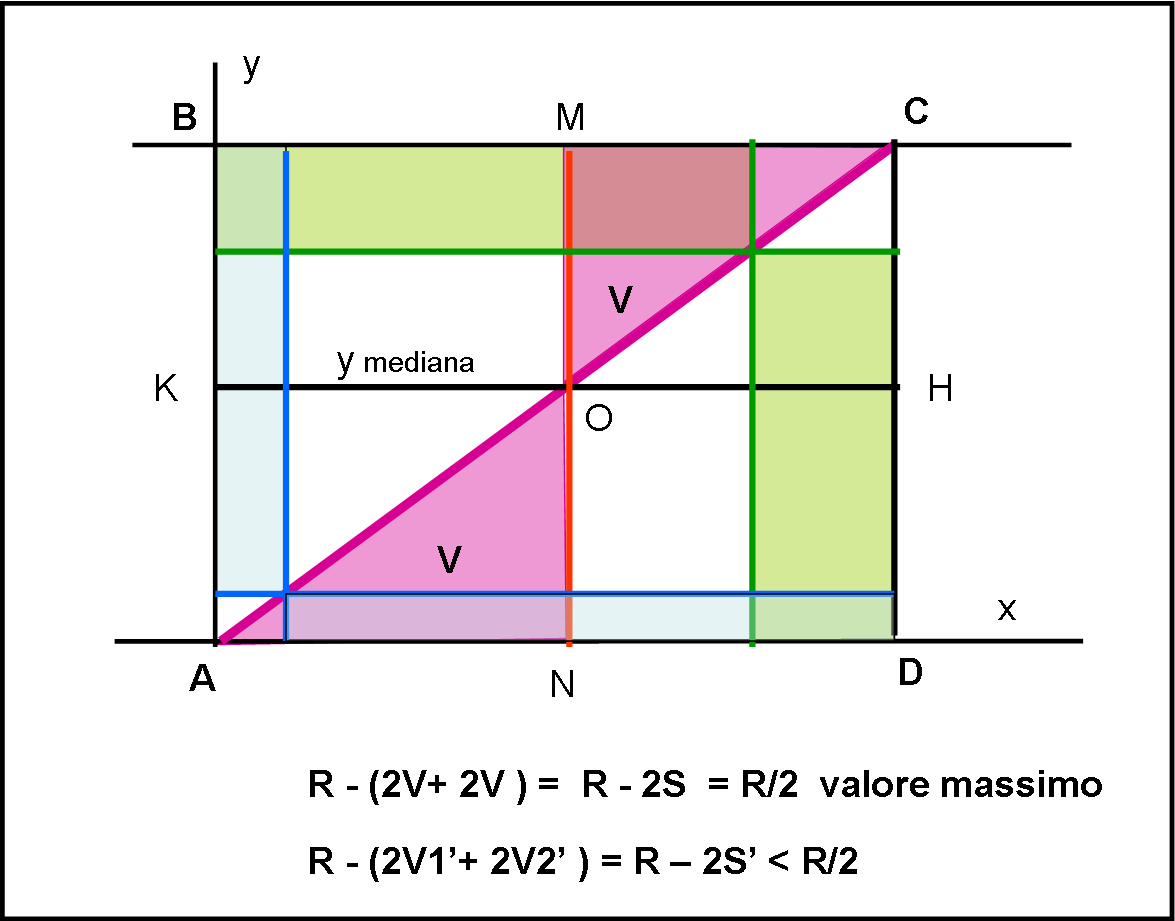
Tracciamo la y mediana KH. Essa individua le due aree relative al nostro problema, V1 = V2 = V (AON = MOC, in viola). La loro somma sia S.

Se chiamo R l’area del rettangolo ABCD, posso scrivere (OCH = OMC):

R – 2S =  R/2                    …. (1)

L’area R/2 è per costruzione geometrica l’area massima ottenibile (mezzo rettangolo iniziale)

Per qualsiasi valore di y, sopra o sotto la y mediana, abbiamo sempre  (riga verde e riga azzurra):

R – 2S’ = R’/2 < R/2        …. (2)

Dove R’/2 è la somma delle aree dei rettangoli (azzurri o verdi) rimanenti, sempre minore di R/2

Facendo la differenza tra (1) e la (2) abbiamo:

- 2S + 2S’= R/2 – R’/2 > 0

S’ – S > 0      sempre

Ossia qualsiasi S’ è maggiore di S.

La parte precedente è servita solo per rendere più semplice la trattazione, limitandosi a una retta, ma niente cambia se partissimo direttamente da una funzione qualsiasi f(x)

Confermiamo, allora, il risultato in modo ancora più immediato e applichiamolo direttamente per qualsiasi curva crescente f(x) utilizziamo il metodo che possiamo vedere nella Fig. 2b  e  2c, sempre relative alla retta.

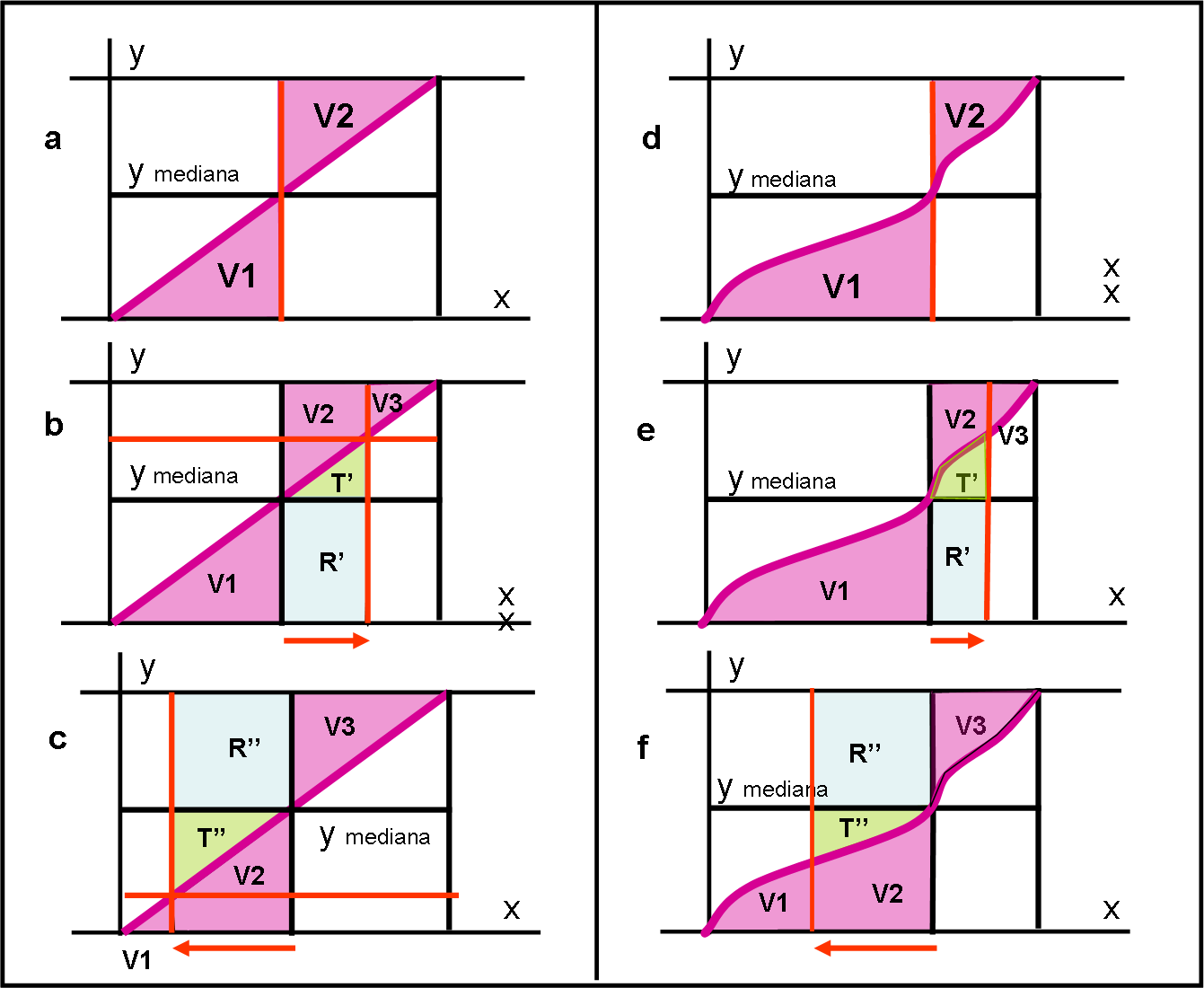
Dividiamo la somma delle aree ottenuta per la y mediana (V1 e V2)  in tre parti e le chiamiamo V1, V2 e V3. Esse vengono definite a seconda della y scelta per tagliare la funzione retta.

Spostando in alto la y (caso b), Abbiamo che la somma delle aree per la y mediana vale:

S = V1 + V2 + V3 = V1 + R’ – T’ + V3             … (3)

Dove il rettangolo R’ azzurro è, per costruzione della y mediana, uguale a quello sovrastante.

La somma delle aree per la y più alta vale:

S’ = V1 + R’ + T’ + V3                …. (4)

Facendo la differenza tra la (4) e la (3) otteniamo:

S’- S = 2T’ > 0                    .... (5)

Situazione analoga capita per la y minore di y mediana.

E’ immediato usare lo stesso procedimento per una curva f(x) qualsiasi, come mostrato  in Fig. 2 (d,e,f). Bastava, perciò, risolvere il per  una funzione del tipo y = ax, ossia una retta.

Tutto resta uguale, a parte il fatto che T’ e T’’ non sono più triangoli… ma la relazione (5) si conserva sempre.

Soluzione di Fabrizio

Seguo l'invito di Umberto di esprimere la soluzione che ho proposto in modo più esteso e confidando di meno nell'intuito visivo.

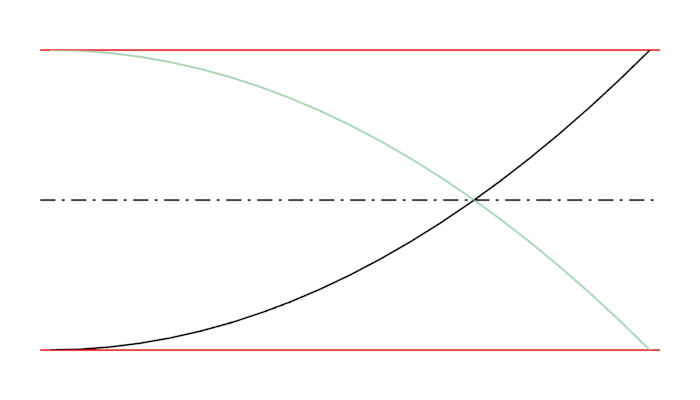
Figura 1

Introduco un asse mediano tra le due rette rosse e traccio una seconda curva (verde) speculare alla curva considerata nel quiz rispetto a questo asse. Questa seconda curva ha 3 proprietà che ci interessano. Queste proprietà derivano direttamente dal modo con la quale l'abbiamo costruita e dal fatto che la prima curva è crescente e continua.

Le due curve si intersecano in un punto che si trova sull'asse mediano.

La nuova curva è sopra l'altra a sinistra del punto di intersezione ed è sotto a destra del punto di intersezione.

La terza proprietà che ci interessa riguarda le aree.

Figura 2a e 2b

L'area sovrastante la prima curva (fig.2a) è uguale a quella sottostante la nuova curva che abbiamo costruito (fig.2b). Questo è vero anche per porzioni di aree ottenute sezionando l'area totale con un segmento verticale (blu).

Da quanto detto sopra segue che l'area totale da considerare nel quiz (A1+A2 di fig.3a) è uguale ad A1+B2 della figura 3b.

Figura 3a e 3b

Ora vediamo come si presentano le nostre aree se scegliamo come retta verticale quella passante per l'intersezione delle due curve che abbiamo tracciato (fig.4a).

Figura 4a e 4b

Per confrontare le aree, in fig.4b sovrapponiamo le aree ottenute in fig.3b e 4a.

La figura è divisa in 3 parti delle due rette verticali che abbiamo utilizzato. Nelle parti a destra e sinistra  le aree di fig.3b e 4a sono identiche. Differiscono invece nella parte centrale.

Per comodità chiamo f la curva originale del quiz e chiamo g la nuova curva (verde). Nella parte centrale l'area in figura 3b è limitata dalla nuova curva g mentre l'area di fig.4b è limitata dalla vecchia curva f.

Poiché siamo prima del punto di intersezione delle due curve ed f è una curva crescente e continua, allora g è sempre maggiore di f in questa sezione della figura. Vale a dire che in questo settore l'area di fig.4a e contenuta in quella di fig.3b. Poiché negli altri due settori le aree sono uguali, l'area totale di fig.4a e contenuta in quella di fig.3b.

Si può ripetere il ragionamento in modo analogo nel caso di retta verticale posta oltre il punto di intersezione con il medesimo risultato finale.

Ne segue che facendo passare la retta verticale (blu) nel punto di intersezione tra f e g si ottiene il minimo  della somma delle due aree del nostro quiz.

Il tutto potrebbe essere tradotto in modo analitico utilizzando le funzioni f(x) e g(x).