Questo articolo è stato inserito nella pagina d'archivio dedicata alla Meccanica Celeste.

 

Un problema di meccanica celeste piuttosto semplice, ma che è della massima importanza non solo per i satelliti artificiali, ma anche per la comprensione di fenomeni astronomici come la strategia utilizzata dai satelliti di Saturno per mantenere "compatto" l'anello f.

Il problema che ci poniamo è abbastanza semplice. Abbiamo un satellite che rivolve attorno alla Terra su un’orbita circolare a un altezza dal suolo uguale a d₁ . Qual è l’energia che bisogna fornirgli per farlo rivolvere a una distanza  d₂ = 2d₁? Aggiungiamo che il raggio della Terra è posto uguale a R (tanto per complicare un pochino...).

Le leggi di Keplero, e non solo, ci dicono che un oggetto in orbita circolare attorno a una massa M ha una velocità maggiore a distanze minori e viceversa. E’ facile ricavare questa conclusione dal calcolo della velocità orbitale che è inversamente proporzionale al raggio (come abbiamo già visto varie volte e rivedremo ancora). Tuttavia, se volessi trasferire il satellite su un orbita più ampia dovrei aumentare il raggio e per far ciò dovrei accelerarlo. Sembrerebbe un controsenso: per portare un satellite su un’orbita più lontana, dove ha una velocità orbitale minore, sono costretto ad accelerarlo, ossia ad aumentare la sua velocità…

Ovviamente, la confusione nasce solo da una scarsa conoscenza della dinamica planetaria

Non è certo la velocità a controllare il moto orbitale, ma è l’energia totale del sistema. Il cambiamento dell’energia dovuto al cambiamento dell’orbita determina la velocità finale. In altre parole, per cambiare orbita devo regalare energia in modo più o meno istantaneo e poco importa l’accelerazione che viene impartita al satellite durante il periodo del trasferimento attraverso una forza più o meno impulsiva. Raggiunta l’altezza necessaria, la forza aggiuntiva si azzera ed è solo la nuova energia raggiunta che regola il movimento del satellite. Da un punto di vista teorico tutto si riduce al calcolo dell’energia necessaria. Da un punto di vista pratico le cose devono essere fatte al momento giusto e nel modo giusto e questo ci permette di introdurre una tipica manovra, quella detta di Hohmann.

Andiamo quindi con calma e prima risolviamo il semplicissimo problema dell’energia necessaria a spostarsi su un orbita più larga.

Regaliamo energia teorica

Il nostro satellite si trova immerso in un campo gravitazionale (conosciamo ormai bene come lavora), ma si sta anche muovendo con una certa velocità V. Ne segue che l' energia totale è composta da due termini: energia cinetica legata alla velocità e energia potenziale legata alla sua posizione rispetto alla massa M della Terra. Non dobbiamo fare altro che scrivere queste due energie e sommarle in modo da avere l’energia totale in una certa orbita.

Per trovare l’energia cinetica è necessario calcolare immediatamente la velocità del satellite. Per farlo basta ricordare che la forza centripeta è in questo caso la forza gravitazionale. In altre parole (come abbiamo già ripetuto spesso e volentieri), il satellite nel suo sistema di riferimento deve imporre l’uguaglianza tra forza gravitazionale (centripeta) e forza centrifuga (deve sentirsi FERMO nel suo sistema).

Basta perciò scrivere la solita formula:

F_C = F_G

mV²/r = GmM/r²        …. (1)

La forza centrifuga deriva dai principi della dinamica che  impongono F = ma, la forza gravitazionale dalla legge di Newton. Ormai questi sono concetti che NOI abbiamo sviluppato parecchie volte e in “molte salse”.

Dalla (1) otteniamo subito la velocità orbitale che è costante nel caso di orbita circolare:

V = (GM/r)^1/2

Da cui l’energia cinetica:

E_C =  ½ m V² = ½ GmM/r

L’energia potenziale dipende solo dall’altezza rispetto alla massa M (a parte m) e vale:

E_P = - GmM/r

Il  meno deriva dal fatto che l’energia potenziale è sempre negativa e diventa zero (ossia è massima) solo all’infinito. Ne abbiamo parlato spesso sia in vari articoli che nel libro della "fisica addormentata".

L’energia totale è quindi:

E = E_C + E_P = ½ GmM/r - GmM/r = - ½ GmM/r       …. (2)

Stiamo lavorando in un campo gravitazionale ed è ovvio che alla fine l’energia totale debba dipendere solo e soltanto dalla distanza dal centro (a parte la massa m ).

Non vi sarà certo sfuggito un richiamo fortissimo al teorema del viriale e il risultato veramente banale e intuitivo. L’energia è sempre negativa dato che il satellite è immesso in orbita circolare (sarebbe negativa anche per qualsiasi curva chiusa e quindi ellittica). Essa diventa zero solo se uguagliamo energia cinetica ed energia potenziale. In tal modo ricaveremmo subito una certa velocità, detta di fuga, che è legata all’orbita degenere che corrisponde al caso di energia uguale a zero: la parabola. Se, infine, l’energia diventa positiva, ossia vince l’energia cinetica, siamo di fronte a traiettorie iperboliche (come quelle che hanno gli asteroidi durante un passaggio ravvicinato a un pianeta, effettuato a grande velocità).

Bando alle “ciance” e torniamo al nostro problemino.

Per essere più corretti, scriviamo la (2) con i dati di partenza. La Terra ha un certo raggio R e l’altezza orbitale d1 è misurata dalla superficie. Ne deriva:

E₁ = - ½ GmM/(R + d₁)

Cosa vogliamo ottenere a questo punto? Solo e soltanto che l’orbita circolare si effettui a una distanza d₂ = 2d₁ dalla superficie terrestre. L’energia totale legata a questa nuova configurazione non è altro che:

E₂ = - ½ GmM/(R + d₂) = - ½ GmM/(R + 2d₁)

Sembra proprio di aver scritto una banalità. E così è, infatti. La confusione che si fa spesso è del tutto assurda. Tuttavia, in queste formulette così “ridicole”  sonnecchiano all’interno concetti fondamentali come la conservazione dell’energia, il guadagno di energia potenziale a discapito dell’energia cinetica (se vado più lontano, devo viaggiare più lento), ossia le celebri “montagne russe”. Per non parlare di momento angolare… Spostare un oggetto su un’orbita superiore vuol dire cambiargli il momento angolare (NON si conserva, dato che vi è una forza impulsiva esterna). Ma il momento angolare è legato alla distanza dal centro e quindi il satellite guadagna momento angolare.

Abbiamo calcolato l’energia totale iniziale e quella totale finale (entrambe minori di zero, essendo su orbite circolari). Qual è l’energia che dobbiamo impartire al satellite per eseguire il trasferimento di orbita? Veramente banale: la differenza tra le due energie!

ΔE₁₂ = - ½ GmM/(R + 2d₁) + ½ GmM/(R + d₁)

ΔE₁₂  =  GmMd₁/(2(R + 2d₁)(R + d1))

Com’è facile calcolare l’energia da regalare al nostro satellite per farlo rivolvere su un’orbita più alta! Da un punto di vista teorico abbiamo ragione. Da un punto di vista pratico le cose si complicano abbastanza, dato che dobbiamo effettivamente impartire delle velocità al satellite (non per altro si parla di ΔV nelle manovre orbitali) per poterlo muovere nello spazio (sono proprio loro che determinano uno spostamento in funzione del tempo). Si deve, perciò, agire in momenti particolari e con valori particolari, per potere ottenere alla fine proprio la differenza di energia necessaria.

Accenniamo solo a uno di questi sistemi, il trasferimento alla Hohmann

Regaliamo energia in modo pratico

Abbiamo visto che ad ogni orbita corrisponde una certa energia e, di conseguenza, una certa velocità del satellite, in accordo con la legge del moto. Più in generale, se l’orbita fosse ellittica, la velocità cambierebbe da punto a punto, raggiungendo il valore massimo al perigeo e il valore minimo all’apogeo. Problemi? Direi proprio di no. Al perigeo il satellite è più vicino alla Terra e quindi va più veloce; all’apogeo è più lontano e quindi va più lento. Tuttavia, l’energia orbitale è quella che è: ogni orbita ha la sua energia.

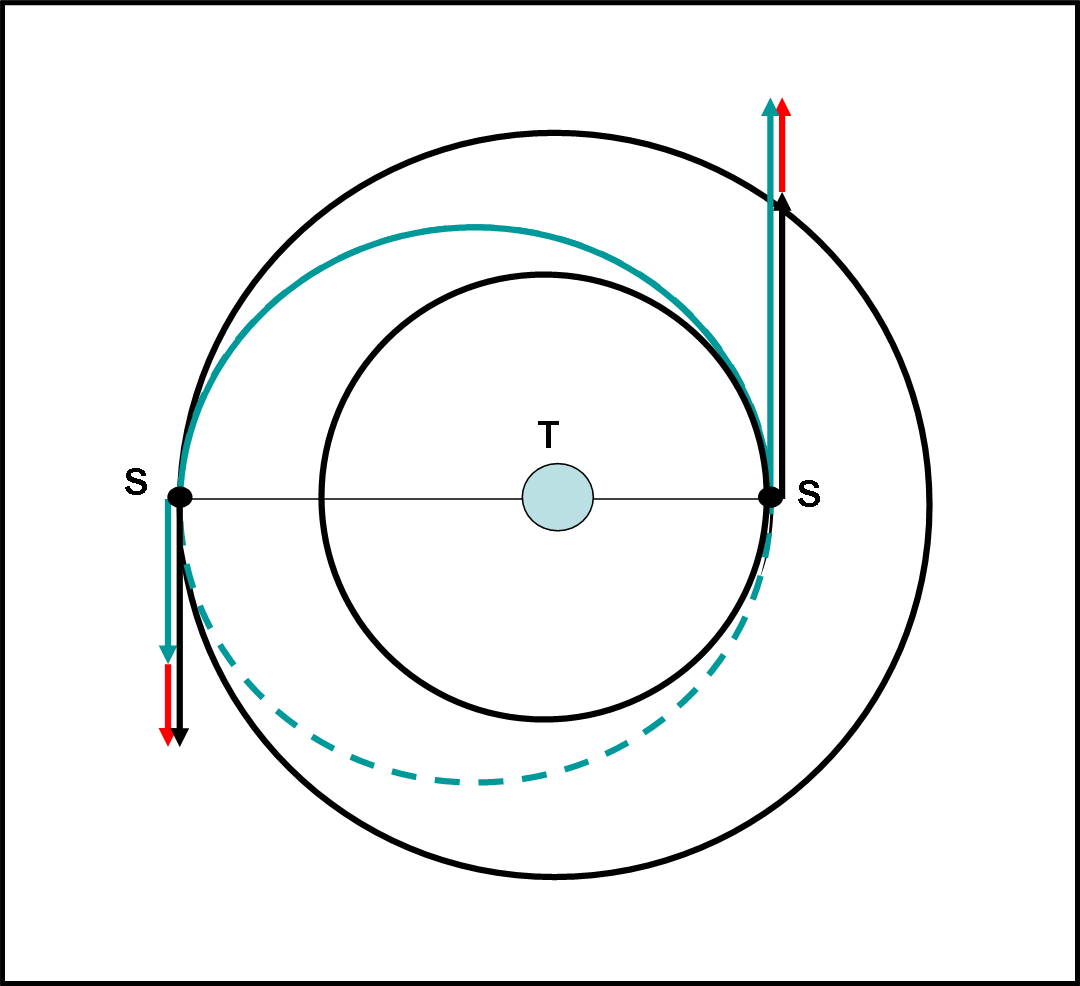
Il regalo di energia va quindi dato al momento giusto e nel modo giusto, agendo su ciò che è ottenibile con i motori, ossia una variazione di velocità. Seguiamo in modo semplificato ciò che si deve fare, utilizzando la figura che segue…

Il satellite rivolve sull’orbita nera interna con una certa velocità nera. Agiamo, impartendo una certa velocità attraverso i razzi, indicata dalla freccia rossa. Otteniamo una velocità azzurra. Essa è esattamente la velocità che ha il satellite quando si trova al perigeo dell’orbita ellittica azzurra. Esso descrive allora quest’ellisse fino a giungere all’apogeo con una velocità decisamente più bassa. Impartiamogli allora una seconda velocità rossa in modo da fargli ottenere la velocità che avrebbe un satellite posto in quella posizione in moto circolare attorno alla Terra. A questo punto il satellite si muove con la freccia nera esterna e descrive un’orbita circolare esterna. Notiamo che quest’ultima velocità è minore di quella che aveva sull’orbita iniziale. Giocando con le velocità al perigeo e all’apogeo di un orbita ellittica di trasferimento siamo riusciti a ottenere una velocità minore di quella iniziale pur impartendo sempre impulsi di velocità positivi nei posti giusti e al momento giusto.

Si è dimostrato perfettamente che dare velocità a un satellite,  per farlo salire e viaggiare a velocità più bassa, NON è assolutamente un’assurdità. Tutto il gioco sta sull’energia finale e sul metodo usato per ottenerla. Ottenuta l’energia necessaria, la velocità ne è una conseguenza. In fondo è sempre la stessa storia: si perde in energia cinetica e si guadagna in energia potenziale.

Ovviamente, dato che la fisica non è opinione, parlare di energia acquisita o ceduta si traduce immediatamente in acquisto o perdita di momento angolare a seguito del cambiamento delle condizioni. La forza che è stata impartita non passa per il centro di rotazione e quindi ha regalato momento angolare con le ovvie conseguenze su velocità di rivoluzione (tutto torna sempre).

I pastori energetici

A questo punto possiamo applicare il tutto all’anello f, ai suoi pastori , approfittando delle nuove ipotesi sulla loro  origine.

Ne abbiamo già parlato in vecchi articoli, ma non è mai male ripetere certi concetti, soprattutto dopo che ne abbiamo dato una visione fisica e matematica. Accenniamo quindi al meccanismo di confinamento che permette di sopravvivere all’anello f e descriviamo brevemente le ultime scoperte a riguardo che sembrano definire la tempistica della sua formazione.

Come detto e ripetute varie volte, l’anello f di Saturno non dovrebbe esistere. Esso è troppo stretto e l’unica possibilità perché lo si sia osservato così ai tempi dei Voyager sembrava, in un primo tempo, essere dovuta a una sua nascita molto recente. E’, però, troppo difficile avere una tale fortuna osservando l’Universo e i suoi tempi ben più lunghi dei nostri e, quindi, ne seguiva che doveva esserci una soluzione diversa, legata a qualche processo di meccanica celeste non ancora conosciuto.

Il problema di fondo è che un anello può anche nascere molto stretto a seguito della frammentazione di qualcosa, ma in breve tempo esso tende ad allargarsi rapidamente, come capita nel sistema ben più noto degli anelli principali di Saturno. Ciò dipende da molti fattori, non ultimo quello delle collisioni mutue tra gli stessi frammenti. La soluzione che venne proposta sembrava alquanto macchinosa e puramente teorica: era necessario che qualcosa facesse da pastore a quel gregge di pecorelle-frammenti e riuscisse a mantenerle quasi perfettamente in fila, senza lasciarle vagare nei “campi” circostanti in cerca di erba più verde e saporita.

I due pastori non potevano che essere due satelliti, uno esterno e uno interno, tali che fornissero e togliessero energia alle pecorelle più agitate e le rimettessero nel gregge. Qualcosa di simile a quello che abbiamo visto nel trasferimento orbitale, dove è necessario frenare o accelerare un satellite per fargli cambiare orbita: regalo o furto di energia (o alternativamente, ma è la stessa cosa, di momento angolare).

I frammenti dell’anello f, però, non hanno motori né razzi e quindi l’energia richiesta deve provenire dai due satelliti pastore. Anch’essi non hanno molte possibilità per agire sulle pecorelle a distanza, ma gli basta e avanza la forza di gravità. Esssi sono ben più massicci dei frammenti dell’anello e quindi possono competere con Saturno quando si trovano molto vicini alle pecorelle vagabonde. Il gioco meccanico si riferisce alla legge di Newton (o -se preferite- alle leggi di Keplero) che ci dice che chi orbita più vicino al pianeta dominante è costretto a viaggiare a velocità maggiore di chi sta a distanza maggiore.

Ne segue una situazione abbastanza semplice: arrivando da Saturno, prima troviamo il satellite-pastore interno, poi l’anello e infine il satellite esterno. Il primo satellite ha velocità orbitale maggiore di quella delle pecore che , a loro volta, hanno velocità maggiore di quella del satellite esterno.

A cosa porta questa configurazione? Semplice: un frammento dell’anello viene raggiunto e superato dal satellite interno, mentre raggiunge e supera il satellite esterno. Prendiamo allora due pecore che si sono spinte verso l’interno e verso l’esterno e tendono a disperdere il gregge. Quella più interna tende ad allontanarsi verso Saturno, finché non sopraggiunge il pastore interno e la sua forza di gravità. All’inizio tende a tirare verso di lui la pecorella (ossia la rallenta), ma poi la supera e la lascia dietro, sempre di più.

Questa è la fase fondamentale e anche l’ultima ad accadere prima dell’allontanamento di pecora e pastore. Il satellite trascina verso di sé il frammento e gli impartisce un’energia supplementare (come faceva il razzo del satellite). Maggiore energia vuol dire allontanamento da Saturno e trasferimento su un’orbita più distante, ossia proprio quella delle pecorelle più tranquille allineate.

Analogamente, potremmo dire che viene ceduto momento angolare al frammento che, quindi, tende ad allontanarsi da Saturno. Il succo è lo stesso. Tralasciamo il processo matematico e fisico più accurato che necessita di passaggi intermedi (anche se non proprio orbite alla Hohmann) e concludiamo con la configurazione finale: la pecorella agitata viene rimessa rapidamente in gruppo.

Un sistema uguale e opposto viene utilizzato dal satellite esterno. Esso viene superato dal frammento. All’inizio la pecorella viene trascinata, ma dopo poco (al momento del sorpasso) comincia a essere rallentata nel suo moto a causa della gravità del satellite che tende a trattenerla. Il frammento perde, quindi, energia e si trasferisce su un’orbita più interna, tornando anch’esso nel gruppo. Il sistema di “controllo” del gregge viene ripetuto ogni rivoluzione dei pastori e quindi continua implacabile. L’anello f rimane stretto!

Come dicevo prima, sembrava un processo troppo elaborato e poco naturale, ma il sistema di Urano con tutti i suoi anelli sottili e pastori vari ha dimostrato che la Natura voleva proprio divertirsi con queste configurazioni quasi “magiche”.

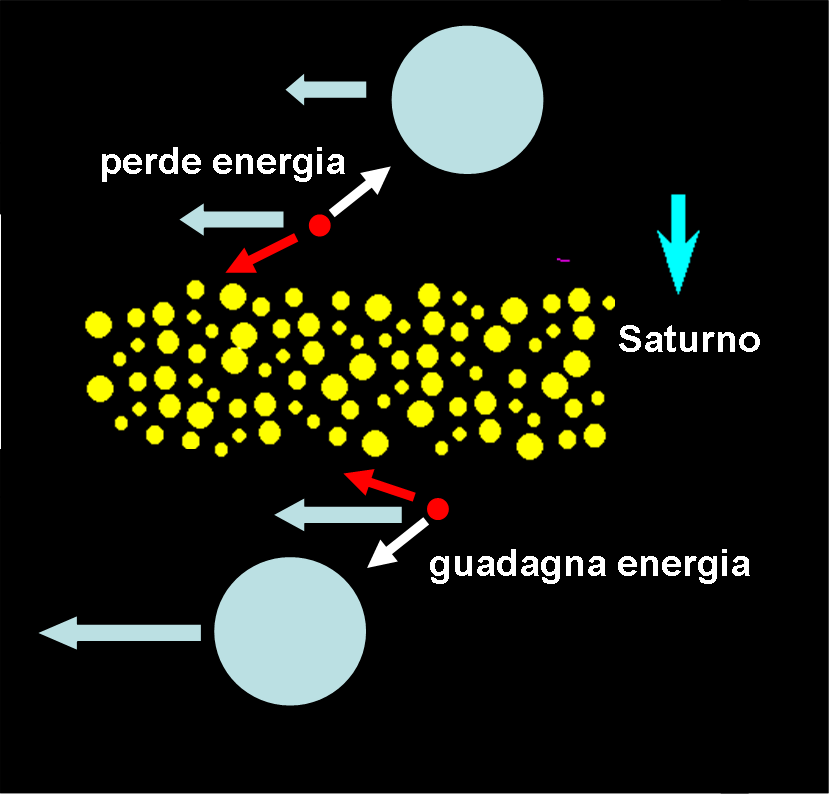
La figura che segue illustra il meccanismo in modo estremamente semplice.

Veniamo adesso alla formazione di un sistema così apparentemente bizzarro. La prima cosa molto importante è la distanza da Saturno. Essa è “circa” quella del limite di Roche, ossia il punto di non ritorno di un oggetto piuttosto grande. Al suo interno le forze di marea potrebbero facilmente disintegrarlo, mentre al suo esterno potrebbe rimanere intatto. Le condizioni sono, perciò, decisamente particolari, ma sufficienti per creare satelliti abbastanza massicci. Essi si sarebbero formati ai limiti esterni dell’anello principale di Saturno e sarebbero poi migrati verso posizioni più tranquille esterne. A quel punto vi sarebbero state collisioni tra loro (e i loro antichi progenitori) capaci di creare attraverso i residui l’anello f, tenuto “in riga” proprio da coloro che lo hanno formato.

In conclusione, un problema simile a quello dell’uovo e della gallina (è nato prima l’anello o i satelliti) si risolve con la vittoria della gallina (anzi delle galline): prima si sarebbero formati satelliti che poi scontrandosi avrebbero prodotto l’anello  e infine sarebbero rimasti solo in due a fargli la guardia. Il nucleo abbastanza denso dei satelliti è pienamente d'accordo con le previsioni teoriche e con il  modello elaborato.

Insomma, il Sistema Solare sa fare magie eccezionali e riesce a farle con il poco materiale (e le leggi fisiche) a disposizione!

Articolo originario QUI