Un quiz.. da manicomio!
Dopo un quiz rilassante.. un quiz che può portare al manicomio! La domanda è difficile ma in realtà la soluzione è semplice. Ecco qua la domanda :
Trovare tutte le funzioni per le quali, qualsiasi siano
, valga la seguente diseguaglianza:
il quiz richiede una conoscenza approfondita delle funzioni, comunque a livello di scuola superiore. Come detto altre volte siamo in un isola deserta.. niente computer, niente software 3D o 2D o altro. Solo un pezzo di carta, una matita e tanta fantasia matematica!
32 commenti
Ispirato dalla soluzione data da Enzo al quiz rilassante sono arrivato alla mia ipotesi di soluzione che scrivo sotto in testo nascosto. Credo che non ci si possa muovere molto.
x1-x2=Δx x1=x2+Δx
F(x2+Δx)-F(x2)≤Δx^2
Divido per Δx
per Δx>0 [F(x2+Δx)-F(x2)]/Δx≤Δx
per Δx<0 [F(x2+Δx)-F(x2)]/Δx≥Δx
Per essere valido sia a destra che a sinistra rimane solo l'uguale.
Deve valere anche per Δx minore di un epsilon qualsiasi, che è la definizione di derivata.
dF(x)/dx=0 ovunque quindi F(x) deve essere costante.
Testo scoperto alle 18:19
ok Fabrizio; non posso dire niente per ora, ma lo sai certamente da solo,meglio di me. Poi mi spiegherai però cosa centra la soluzione di Enzo al quiz rilassante.Io questo non l'ho capito.
Un chiarimento: una funzione che soddisfa strettamente la condizione posta, cioè per la quale si ha:
f(x1)-f(x2)<(x1-x2)^2
va bene ?
se soddisfa il < soddisfa anche il <=
il problema è trovarla. Questo fatto restringerebbe le possibilità
In questo momento non posso pubblicare figure, cerco di spiegarmi con il solo testo.
Con riferimento, per esempio, alla funzione y=x, se prendo due ascisse x1 e x2 e ne calcolo i corrispondenti valori, poichè si tratta del grafico della bisettrice del primo e terzo quadrante, avrò ovviamente:
f(x1)-f(x2)=(x1-x2)
Allora, se la quantità (x1-x2) è già uguale a f(x1)-f(x2), a maggior ragione la quantità (x1-x2)^2 sarà maggiore di f(x1)-f(x2). Questo per qualunque valore di x1 e x2 (l'angolo di inclinazione della retta è costante). Quindi sembrerebbe che la funzione y=x soddisfi strettamente la condizione posta.
Stesso ragionamento , grafico, anche con tutte le funzioni rappresentate graficamente da rette inclinate meno di 45 gradi rispetto all'asse x. Tutte queste funzioni soddisfano strettamente la condizione posta. Cioè, per qualsiasi valore di x1 e x2, la quantità f(x1)-f(x2) sarà sempre minore di (x1-x2)^2.
Con rette inclinate rispetto all'asse x di un angolo maggiore di 45 gradi, invece, ci sono valori di x1 e x2 per i quali si può verificare anche l'uguaglianza.
Ma chissà se ho capito bene la richiesta.
a richiesta l hai capita senz altro, ma deve valere qualsiasi siano x1, x2. Se la differenza tra i due diventa minore di 1..
ma x1 può essere preso anche maggiore di x2 ? Io ho dato per scontato x1<x2.
Infatti, per la funzione y=x, se prendo x1=2 e x2=5/2 (x2-x1 < 1 e x1<x2) continua a verificare la condizione
f(x1)-f(x2)<(x1-x2)^2
Invece, se prendo x1=2 e x2=3/2 (sempre x2-x1<1 ma x1>x2) allora la condizione non è più verificata.
si x1 e x2 possono assumere qualsiasi valore. Non farti ingannate dall indice.
ah beh, allora l'unica possibilità penso sia quella della funzione costante y=k , con k qualsiasi. In questo caso avremmo, come grafico, una retta parallela all'asse x. Per qualunque valore della differenza x1-x2 (con x1>x 2 o x1<x2) avremmo ovviamente f(x1)-f(x2)=0, sempre < (x1-x2)^2 tranne che nel caso x1=x2 in cui varrebbe il segno di uguaglianza.
si Arturo, ma ricordati che il problema richiede tutte le funzioni. Dobbiamo assicurarci che non ce siano altre.
Sembra giunto il momento di dare un piccolo suggerimento, così poi potremmo schiarire il commento di Fabrizio, che anticipa già il metodo di risoluzione. Pensiamo alle derivate...altrimenti non ne usciamo fuori.
Sembra giunto il momento di dare un piccolo suggerimento, così poi potremmo schiarire il commento di Fabrizio, che anticipa già il metodo di risoluzione. Pensiamo alle derivate...altrimenti non ne usciamo fuori.
Mi hai bruciato sul tempo, Umberto. Guardando la condizione, in effetti, avevo pensato di scrivere (x1-x2)^2 come (x1-x2)*(x1-x2) e portare uno dei due fattori al denominatore del primo membro. A quel punto, vedo a numeratore la differenza f(x1)-f(x2) e al denominatore (x1-x2). Se faccio tendere a zero la differenza x1-x2 a primo membro mi viene fuori proprio la derivata di f(x) . Poiché, poi, hai detto che x1 e x2 possono essere qualsiasi, allora perché la condizione sia verificata e poiché a seconda che sia x1<x2 o x1>x2 si ha che la differenza x1-x2 è maggiore o minore di zero, per cui si cambia il verso della disequazione, alla fine la condizione è verificata solo se f'(x)=0. Cioè, f(x) = k.
(qui temperatura in aumento, previsti 36 gradi nel week end, il prossimo quiz dovrà essere fresco :-) )
complimenti Arturo, più o meno é proprio cosi. Bisognerà poi citare il teorema fondamentale del calcolo
Fabrizio quando vuoi schiarire il tuo commento.. C e pero qualcosa che non mi convince del tutto. Ma lascio a te rivedere.
Ho scoperto il testo del mio primo commento.
ok grazie. Ti dicevo che c'è qualcosa che non va nella prima parte pur essendo giusta la conclusione.
Ci sto pensando, ma ancora non ho trovato cosa potrebbe essere.
Ho ripercorso i passaggi, ma non sono riuscito a trovare cosa non va.
Forse ci potrebbero essere due passaggi da chiarire.
Nella seconda riga x2 è la variabile indipendente, invece della usuale x, e Δx è la sua variazione. Ma è solo una denominazione delle variabili per continuità con quelle iniziali.
Il secondo punto è il passaggio al limite (Δx minore di un epsilon qualsiasi) dove ho esplicitato il solo termine a sinistra che è la derivata dF(x)/dx. Il termine a destra è proprio Δx che tende a 0.
ho un dubbio sui primi passaggi; io ho trovato che quel rapporto è limitato in modul0 da |x1-x2|, tu dici che è uguale. Quindi arriviamo alle stesse conclusioni se x1-->x2.
La tua condizione è però più forte; dice addirittura [F(x2+Δx)-F(x2)]/Δx=Δx, ma questo non so se è vero.
Ragionando a posteriori, visto che troviamo una F costante, anche se x1<>x2, [F(x2+Δx)-F(x2)]=0, [F(x2+Δx)-F(x2)]/Δx=0, ma Δx<>0,quindi non vale l'eguaglianza.
Oppure dimmi tu dove sto sbagliando io.
Dalla tua osservazione vedo che ho anticipato la frase "Per essere valido sia a destra che a sinistra rimane solo l'uguale." Questa frase si riferisce al limite (destro e sinistro) e non alle disuguaglianze con Δx qualsiasi, quindi dovrei spostarla più avanti.
quando hai tempo se vuoi puoi riscriverlo in un nuovo commento
grazie
Ripropongo la mia risposta rivista a seguito del commento di Umberto.
Faccio le due sostituzioni seguenti nella disuguaglianza del quiz:
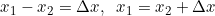ed ottengo:
-F(x_2)\leq&space;\Delta&space;x^2)
Divido per Δx entrambe i lati facendo attenzione all'effetto sul verso della disuguaglianza. Ridenomino anche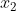
che non ha più bisogno del pedice essendo rimasto solo.
Queste relazioni devono essere valide per qualsiasi valore di
L'espressione a sinistra della due disuguaglianze sono la definizione di derivata di F(x) rispettivamente a destra e a sinistra del punto x.
A destra di x dovrebbe valere}{dx}\leq&space;0)
ed a sinistra di x dovrebbe valere }{dx}\geq&space;0)
.
Affinchè la derivata esista in x,)}{dx}=&space;0)
a destra ed a sinistra per ogni valore di x, quindi F(x) deve essere costante. La scelta di F(x)=k è anche consistente con qualsiasi valore finito di Δx , positivo o negativo: -F(x_2)=0\leq&space;\Delta{x}^2)
poiché il valore a destra è sicuramente positivo.
Esisterebbe anche la possibilità di funzioni con la derivata a destra di x diversa da quella a sinistra di x. Niente di strano se non fosse che questo deve valere per ogni valore di x. Forse matematicamente esiste, ma è difficile da visualizzare. Inoltre mi sembra di dubbia consistenza per valori finiti di Δx.
ok Fabrizio grazie . Lo leggerò attentamente.
Fabrizio non può dividere per zero. Il quiz è ambiguo se x1=x2 in quanto in questo caso qualsiasi funzione limitata soddisfa la disequazione. 0=0.
penso che sia implicito che deltax<> 0. Cechiamo il limite del rapporto. Deve essere un errore di scrittura
Leandro, giusto.
Le due disuguaglianze valgono per Δx>0 e per Δx<0 e non per Δx=0.
Credo che le condizioni che ho scritto sopra possano essere rese più stringenti basandosi su questo fatto:-F(x_2)\leq&space;(x_1-x_2)^2)
deve valere per ogni coppia di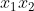 
, deve valere anche scambiando la coppia. Poiché ^2=(x_2-x_1)^2)
, possiamo scrivere
^2\leq&space;F(x_1)-F(x_2)\leq&space;(x_1-x_2)^2)
se
Quandi le condizioni diventano:
-F(x)}{\Delta&space;x}\leq&space;\Delta&space;x)
Passando al limite per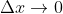
otteniamo che deve valere la stessa condizione sia per la derivata a sinistra sia per la derivata a destra:
}{dx}\leq&space;0)
Dovendo valere per ogni x, segue che l'unica soluzione è F(x)=costante
adesso hai centrato il dilemma! la soluzione sta proprio in quello scambio di coppia, che fa si che il modulo di quel rapporto sia limitato. io ho fatto in modo leggermente diverso ma il trucco sta proprio li. Questa soluzione è quella che va meglio.
ok . Io comincio a scrivere la soluzione. Se qualcuno comunque vuole aggiungere qualcosa faccia pure.ufficialmente consideriamo però chiuso il quiz.
Secondo me non è detto che la soluzione debba essere una funzione costante in R.
Anche y=[x] (parte intera di x) funziona, così come molte funzioni costanti a tratti.
L'errore è stato ipotizzare che la derivata ESISTA per ogni x, perché se, per esempio, la derivata non esistesse per valori interi di x, la funzione non sarebbe più costante in R. Ricordo che se la derivata è nulla per ogni x CHE APPARTIENE AD UN INTERVALLO, la funzione è COSTANTE IN QUELL'INTERVALLO. Quindi una derivata nulla per ogni x non intero non implica necessariamente che la funzione sia costante in tutto il dominio, ma solo in ognuno degli intervalli dove la derivata è nulla.
Più in generale, direi che la funzione debba essere costante a tratti, con tratti di ampiezza non minore di 1, in modo che la differenza x1-x2, se positiva, sia minore del proprio quadrato.
Uhm... come non detto...avevo invertito il verso della disuguaglianza...