Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

Riprendo in sintesi quanto fatto nella prima parte dell'articolo. Si definiscono numeri trascendenti quei numeri  reali che non sono algebrici, ovvero non sono soluzione di alcuna equazione algebrica a coefficienti interi. Cantor riusci a dimostrare che i numeri trascendenti sono infiniti, anzi  sono più che numerabili.

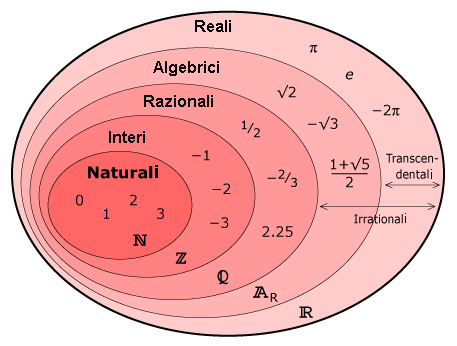
Infatti se chiamiamo A l'insieme dei numeri algebrici e T l'insieme dei numeri trascendenti, T=R\A. Abbiamo visto che A è numerabile. Di sicuro T non può essere numerabile o finito, perchè altrimenti R=T U A sarebbe unione di due insiemi numerabili e pertanto sarebbe numerabile. Quindi T è infinito ed ha cardinalità maggiore di N. Non possiamo però dire subito che T ha la cardinalità di R , escludendo cardinalità x comprese fra il numerabile e il continuo, ovvero |N|<x<|R|. (questo dilemma è noto come Ipotesi del continuo).

Dobbiamo perciò dimostrarlo. Facciamolo in modo generico, staccandoci dal nostro caso particolare.

Prima una osservazione. Consideriamo un insieme A infinito. Vogliamo dimostrare che contiene un insieme numerabile. Se procediamo formalmente, dovremmo creare una funzione ricorsiva che però non  so se piaccia a tanti. Possiamo dimostrarlo in modo più intuitivo.

Vogliamo trovare una funzione iniettiva di f: N--->A. Se A è infinito, senz'altro non è vuoto.   Scelgo allora un elemento di A che chiamo f(0). f(0) è quindi l'immagine di 0. Poi scelgo un elemento f(1) diverso da f(0) , e che diventa l'immagine di 1. Continuo così; f(n) altro non è che un elemento di A diverso da tutti i precedenti, ovvero appartenente  a A\{f(0),f(1),...f(n-1)}. Posso fare queste infinite associazioni perchè A è infinito, quindi riesco sempre a trovare un elemento che sia diverso da tutti quelli scelti in precedenza.  Quindi l'applicazione così costruita è iniettiva, ed è anche biunivoca su f(N). Quindi l'insieme f(N) è l'insieme cercato, ovvero un insieme numerabile sottoinsieme di A.

Adesso sia X un insieme infinito, Y un insieme numerabile (nel nostro caso X=R, ma ormai che ci siamo vogliamo dimostrare una cosa generica). Dimostriamo che |X\Y |=|X|, ovvero che la cardinalità di X\Y è uguale a quella di X.

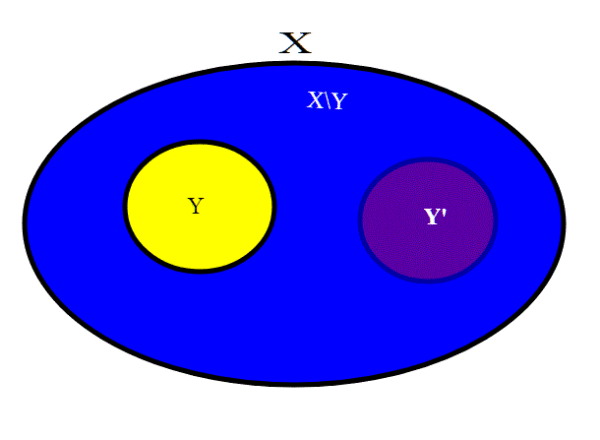
Per quello che abbiamo visto sopra, essendo X\Y infinito, esiste un sottoinsieme di X\Y che chiamiamo Y', che è numerabile. Y' è disgiunto da Y.Se Y' è numerabile, esiste allora una funzione biunivoca f fra f: Y'--->Y'  U  Y; infatti anche Y'  U  Y è numerabile, essendo unione di insiemi numerabili.

Per dimostrare che |X\Y |=|X|, dobbiamo trovare una funzione biunivoca g che va da g:X\Y--->X.

La definiamo così:(g è definita su Y' U (X -(Y U Y'))=X\Y)

g(x)=f(x)  se      ; sappiamo che f(x) copre Y'  U  Y, inoltre è iniettiva

g(x)= x se  ; la funzione x (identità) copre tutto ed è iniettiva

ma allora Y'  U  Y U  =X, quindi g è suriettiva su X, ed è inoltre iniettiva. Quindi è una biezione,

g:X\Y--->X

I numeri trascendenti hanno la stessa potenza del continuo.

Nel nostro caso, X è l'insieme R dei reali. Y è invece A, insieme dei numeri algebrici. X\Y rappresenta per noi R\A=T, insieme dei numeri trascendenti. Quindi l'insieme dei numeri trascendenti ha la stessa potenza del continuo. All'interno dei reali, ci sono dunque più numeri trascendenti che altro.