Categorie: Cosmologia Spazio-Tempo
Tags: distanze cosmiche espansione Universo Universo Osservabile
Scritto da: Maurizio Bernardi
Commenti:2
TOPOGRAFIA COSMICA: Il problema da risolvere **
Non fatevi spaventare dal fantascientifico effetto Keplero-Kranz che regolerebbe la struttura granulare sferica del micro e macrocosmo, cari amici lettori... non vi chiederemo di calcolare il fantasioso spazio interstiziale tra una bolla di Universo ed un'altra, né di risolvere il problema della valorizzazione dinamica delle proprietà cosmiche. Leggete fino in fondo questo raccontino di fantascienza e capirete!
Grimilde Kranz alzò la testa, incorniciata da una incredibile treccia bionda alla Tymošenko, dal grande tavolo luminoso su cui si stava evolvendo la sconcertante immagine 3D di un grappolo di sfere in lievitazione.
In questa storia, in questo universo alternativo, il Big Crunch non era avvenuto. L'Universo continuava ad espandersi sempre più velocemente e gli affari della Immobiliare Unlimited continuavano ad andare a gonfie vele.
Grimilde aveva ereditato il ruolo di Amministratore Delegato dalla madre Adolfa (che lo aveva ereditato da sua madre Agnes, che lo aveva ereditato da sua madre Bertha, che lo aveva ereditato da sua madre Ermlinde, e così via, per migliaia di generazioni, fino ad arrivare alla capostipite Isotta, che aveva avuto l'idea dalla quale tutto era iniziato), ma la sua vera passione non erano le strategie immobiliari, bensì la ricerca cosmologica sul meccanismo dell'espansione accelerata dello spazio.

A soli 22 anni aveva pubblicato un lungo lavoro in cui teorizzava il modello KK (Keplero-Kranz) sulla decompressione dello spazio sferico compattato, come causa prima dell'espansione.
Secondo questo modello lo spazio ha una struttura granulare sferica, a livello microscopico, che obbedisce alla regola del massimo compattamento, ipotizzata da Keplero nella celebre congettura , dimostrata quasi 400 anni più tardi da Thomas Hales. Su questa struttura di base si innesta un meccanismo di crescita continua del diametro dei granuli che tendono a espandersi per occupare quel 26% di spazio interstiziale tra sfera e sfera. Paradossalmente questo ingrandimento produce un volume interstiziale maggiore, ferma restando la percentuale di occupazione dello spazio,
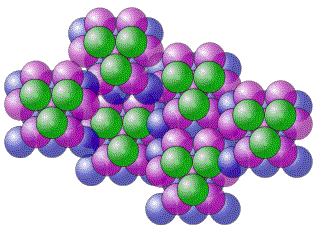
ora più grande.
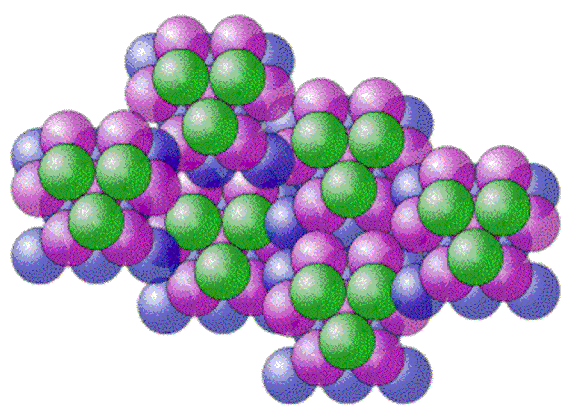
La lievitazione dello spazio avveniva quindi "dal di dentro" e l'effetto cumulativo, a catena, portava alla creazione di nuovo spazio tra le galassie, che era proprio il fenomeno su cui la Immobiliare Unlimited fondava il suo lucroso business.
La conseguenza legale che era inevitabilmente emersa era la seguente: come doveva essere ripartito lo spazio "in più" che si generava? Ogni galassia confinava esattamente con altre 12 galassie (6 la circondavano sul piano equatoriale, 3 la supportavano al suo polo Sud e 3 la sovrastavano al suo polo Nord). Nessun problema per lo spazio interno alla sfera galattica, ma gli interstizi? Come andavano attribuiti? Questo era il perverso problema che, fin da bambina, aveva calamitato l'attenzione di Grimilde: poste 3 sfere sul piano, veniva a formarsi un vuoto centrale, una sorta di triangolo equilatero dai lati concavi; sovrapponendo un quarta sfera e chiudendo, da sotto, con una quinta, lo spazio intrappolato doveva poter venire ripartito tra queste 5 sfere tenendo conto della distanza uniforme dei 9 punti di contatto dal baricentro dello spazio vuoto. Ne risultavano cinque tetraedri uniti per i vertici e con una faccia opposta a ciascun vertice, costituita da un triangolo sferico. Insomma, ciascuna sfera, in questa tassellatura dello spazio veniva ad avere degli "spuntoni", tipo mazza ferrata medievale verso le 12 sfere confinanti.

Questa, più o meno, era la forma dei lotti che venivano assegnati ai clienti della Immobiliare.
Il punto critico era il fatto che complessivamente i volumi continuavano ad aumentare, e a ritmi diversi, a seconda di dove erano localizzati i "terreni". Grimilde aveva dedicato gli anni della giovinezza a cercare la formula per la valorizzazione dinamica di queste proprietà, tenendo conto anche del fatto che la velocità di allontanamento dei lotti galattici, col tempo, sarebbe arrivata a superare quella della luce e anche le misurazioni delle distanze eseguite con il laser non avrebbero più avuto alcun senso.
Secondo i suoi calcoli - tenuti rigorosamente segreti - le comunicazioni tra la centrale del catasto, nella galassia di Andromeda, e il personale periferico decentrato in galassie remote, sarebbero a breve diventate impossibili. Presto la situazione si sarebbe generalizzata alla maggior parte delle proprietà in via di censimento, allora sarebbe esplosa la crisi, dato che nessuno avrebbe potuto valutare nulla, confini, volumi, valori catastali, classificazioni di tipologia galattica: centrale, semicentrale, periferica, insomma: nessuna possibilità di registrazione regolare, il caos totale...
E' a questo terrificante scenario che stava pensando mentre, tirando di nascosto un grande sospiro di sollievo, firmava l'atto di cessione delle proprie azioni della Immobiliare Unlimited alla Immobiliare Cosmos.
***********************************************************************
Fin qui la fantascienza del racconto... ma siamo sicuri che, ben nascosto tra il fantasioso effetto Keplero-Kranz e la centrale del Catasto su Andromeda, il racconto non si ispiri anche a qualche fenomeno fisico scientificamente provato?
Provate, cari amici lettori, a rispondere a queste domande:
- Possono due galassie allontanarsi tra loro più velocemente della luce?
- Se esistesse una galassia che si allontana da noi alla velocità della luce, la potremmo ancora vedere?
- Sarebbe all'interno del nostro Universo osservabile?
- A che distanza si troverebbe?
E se le risposte non le conoscete (o pensate di conoscerle, ma avete dei dubbi), vi consigliamo di leggere questo articolo per le prime tre:
http://www.infinitoteatrodelcosmo.it/2018/01/10/cosa-si-osserva-nelluniverso/
e questo per la n°4
http://www.infinitoteatrodelcosmo.it/2016/10/26/la-sfera-di-hubble-e-tutto-cio-che-non-vedremo-mai/
QUI le risposte alle quattro domande e un approfondimento sul redshift delle galassie in fuga





2 commenti
Caro Mau, vediamo se riesco a rispondere ad alcune domande senza rileggere gli articoli linkati.
Alla prima domanda la risposta è SI, ma, per entrambi, l'altra galassia si trova oltre l'universo (potenzialmente) osservabile dalla propria galassia.
Ma come, direbbe qualcuno, avete così insistito che la velocità della luce è invalicabile ed ora si propone di superarla?
Meglio chiarire subito l'equivoco, nessuno può viaggiare più veloce di un fotone (della luce nella sua visione particellare) nello spaziotempo, ma qui non si stanno indagando i poco significativi movimenti delle due galassie nello spaziotempo, ma la rapidità di dilatazione dello spaziotempo stesso che produce un reciproco allontanamento delle galassie!
Questa rapidità o velocità di espansione dello spaziotempo oggi viene stimata intorno a 71±4 Km/s/Mpc.
E' un po' come dire che ogni milione di Parsec (3,26 milioni di anni luce), lo spaziotempo si espande di 71±4 Km ogni secondo.
Nel frattempo un fotone di una “lontana galassia viaggia verso di noi alla velocità nello spaziotempo è di 299 792, 458 km/s.
E' un po' come dire che il nostro fotone, ogni secondo, ogni Megaparsec è costretto a percorre 71 Km in più.
Dopo 1000 Megaparsec lo spazio in più da percorrere è di 71.000 Km ogni secondo.
Quanti Megaparsec occorrono affinché lo spazio in più da percorrere sia maggiore della velocità del fotone?
Semplice basta confrontare, rapportare, la velocità della luce con la rapidità di espansione dello spaziotempo (un po' come se il nostro fotone camminasse su un tappeto mobile):
(299 792, 458 km/s)/(71 Km/s) = 4 222,428986
Questa quantità di Megaparsec tradotto in anni luce, diventa:
4 222,428986 x 3 260 000 anni luce = 13 765 118 494 anni luce
Anche in questo caso bisogna stare attenti al concetto di distanza, poiché con lo scorrere del tempo le distanze aumentano a causa dell'espansione dell'Universo, per cui una cosa è la distanza tra le due galassie quando il fotone è partito, mentre ben altra è la distanza tra le due galassie quando il fotone è arrivato.
Ciò che stimabile è invece il tempo impiegato dal fotone per raggiungerci, dato che la luce nel vuoto impiega un anno per percorrere un anno luce.
Quindi un fotone partito da una galassia lontana, lontana, al massimo può impiegare 13 765 118 494 anni per raggiungerci, ossia circa 13,76 miliardi di anni (più o meno l'età dell'universo).
Tutto ciò che è oltre tale tempo di percorrenza, ossia oltre tale tragitto, non consente ai fotoni di raggiungerci, poiché l'incremento complessivo di spazio che si frappone aumenta con una rapidità maggiore (velocità di recessione) di quello che la luce può percorrere alla sua velocità.
Dunque le informazioni oltre tale limite, ossia oltre il raggio della sfera di Hubble, non sono accessibili.
Tale ragionamento risponde alla quarta domanda, tenendo conto, però, che la distanza tra le due galassie non è quella attuale (enormemente maggiore), ma il tragitto compiuto dal fotone che deve tener conto della dilatazione dello spaziotempo (13 765 118 494 anni luce).
Per rispondere alla seconda domanda, a mio avviso occorre fare una premessa.
La misura della rapidità di espansione dell'universo (conosciuta come costante di Hubble) non è certa.... Io ho usato 71 km/s/Mpc, ma le misure oscillano tra 67 e 75 Km/s/Mpc, inoltre se si parla di accelerazione della velocità di espansione dell'universo, significa che la costante di Hubble non è stata sempre la stessa nel corso della vita dell'universo.
A me piace pensare che tale accelerazione sia dovuta al fatto che mentre la tensione del vuoto rimane la stessa (considero la dilatazione dello spaziotempo una proprietà intrinseca dello stesso), la materia di diluisce in uno spazio sempre più grande, per cui la curvatura dello spaziotempo dovuta alla presenza di concentrazioni di massa o energia si affievolisce... ma si tratta di una mia opinione, nulla di più.
Al di là delle opinioni, se la costante di Hubble misurata oggi è più alta di quella del passato (a parte la supposta inflazione superluminale iniziale, subito dopo il Big Bang), ciò significa che la luce quando è partita dalla galassia aveva a che fare con una minor dilatazione dello spaziotempo, quindi bisogna intendersi sulla seconda domanda.
Se per galassia che si allontana alla velocità della luce, si considera lo stesso valore della costante di Hubble misurata oggi, allora tale luce ci raggiungerebbe comunque, poiché all'inizio del suo percorso il surplus di spazio era inferiore a quello attuale (espansione accelerata).
Se per galassia che si allontana alla velocità della luce si considera il diverso valore della costante di Hubble con lo scorrere del tempo allora tale situazione andrebbe trattata con i limiti: basta una quota infinitesima maggiore della velocità della luce per impedire che il fotone ci raggiunga e basta una quota infinitesima minore per consentire al fotone di raggiungerci.
Insomma quella lontana galassia che a causa della dilatazione dello spaziotempo si allontana da noi ad una velocità di recessione pari a quella della luce rappresenta un limite non valicabile.
Di sicuro se la luce ci dovesse raggiungere, lo slittamento verso il rosso (redshift) della galassia sarebbe elevatissima, dato che lo stiramento dello spaziotempo allungherebbe oltre ogni limite la lunghezza d'onda della luce (di conseguenza la frequenza luminosa diminuirebbe).
Infine per definire l'universo osservabile si deve tener conto del tempo necessario alla luce per raggiungerci, ossia il cono di luce dell'altra galassia deve poterci intersecare in un certo tempo (se la luce deve impiegare un tempo maggiore dell'attuale età dell'universo, questa potrà raggiungerci solo in futuro).
Bisogna però considerare che nel frattempo l'universo si è espanso dando del filo da torcere al nostro fotone alle prese con un percorso che continua ad aumentare...
Pertanto la galassia primordiale da cui è partito un lontano fotone che ci ha raggiunto solo ora dopo circa 13,7 miliardi di anni, ora a causa dell'espansione dell'Universo si trova a ben altra distanza...
Se l'Universo non si espandesse la luce più lontana (confini dell'universo osservabile) potrebbe arrivare da una distanza massima di circa13,7 miliardi di anni (la sua presunta età), ma dato che questo si espande, a causa di ciò, oggi gli attuali confini dell'Universo osservabile si trovano a circa 47 miliardi di anni (raggio dell'universo osservabile attuale), per cui in totale l'attuale diametro dell'universo osservabile è di circa 94 miliardi di anni luce.
Infine per rispondere alla terza domanda, la galassia con velocità di recessione uguale a quella della luce potrebbe essere visibile nel suo stato primordiale per le ragioni precedentemente esposte, ma all'attuale distanza non sarebbe più visibile nemmeno in un prossimo futuro, poiché la luce dovrebbe fare i conti con una dilatazione dello spaziotempo maggiore della sua velocità.
Spero con il caldo di non aver detto troppe sciocchezze!
Paolo
Caro Paolo, pensavo che i due asterischi ti avrebbero frenato (quiz troppo facile...) ma non avevo fatto i conti con il tuo entusiasmo nei confronti di questo argomento, indubbiamente affascinante.
Per il momento mi astengo dall'entrare nel merito del tuo commento, in modo da lasciare la possibilità ai lettori di cimentarsi nella loro "personale" ricerca di soluzione e ( lo raccomando) di documentarsi, consultando i link suggeriti in cui troveranno una presentazione organica degli argomenti.
Grazie comunque del tuo intervento, che conferma, se ancora fosse necessario, la passione con cui hai costruito una invidiabile competenza in materia.