Soluzione al quiz: Il ritorno dell'ubriaco.
Il quiz richiedeva di calcolare la probabilità di uscire sano e salvo dall'Hotel per l'ubriaco . Riporto lo lo schema del quiz:
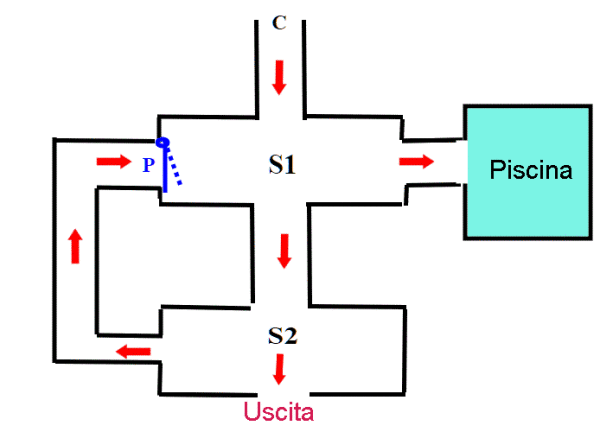
Vorrei per prima riportare la soluzione di Fabrizio, per quanto riguarda il calcolo di tale probabilità. Penso non abbia bisogno di ulteriori commenti:
Partendo dalla sala S1 ci sono 3 esiti possibili per l’ubriaco:
1) finisce in piscina il 50% delle volte
2) trova l’uscita il 25% delle volte
3) si ritrova nuovamente nella sala S1 passando per la porta P il 25% delle volte, e riprende il ciclo.
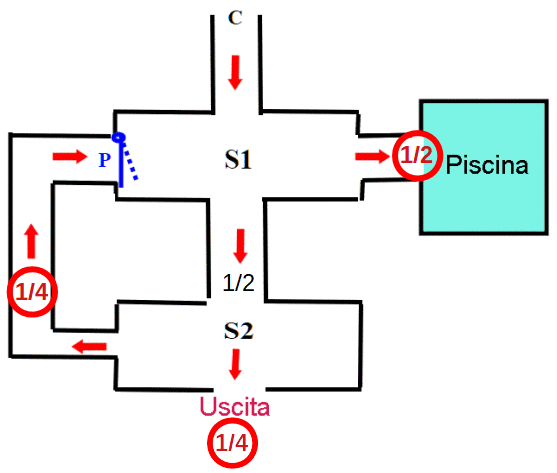
In ciascuno dei giri che fa partendo da S1, la probabilità di finire a bagno in piscina (B) è il doppio di quella di trovare l’uscita (U). Cioè B=2 U, indipendentemente da quanti giri possa avere completato.
Per utilizzare questa relazione occorre rispondere alla seconda domanda di Umberto: “E' possibile inoltre che esso continui a girare all'infinito per S1 ed S2 passando per la porta P e non trovando mai l'uscita ?”
La mia risposta è no. Se un evento è possibile presto o tardi accade. E qui ci sono 2 eventi che fanno uscire l’ubriaco dal giro ed Umberto ha usato la parola infinito. Ovviamente, supponendo che non sia fermato dalla sicurezza dell’albergo o non crolli.
Questo si traduce in un vincolo sulla somma: U+B=1, non essendoci altre possibilità.
Se B=2 U come visto sopra, allora U+2 U=1. U deve quindi essere 1/3, come ha già trovato Gianfranco per altra via.
Fine soluzione di Fabrizio.
Per quanto riguarda la soluzione di Gianfranco, penso che il suo ragionamento sia questo:
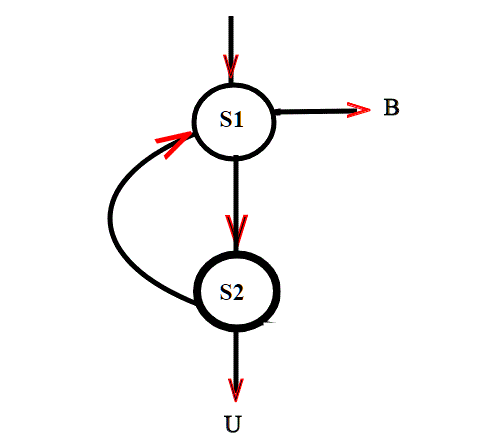
Egli considera la probabilità di uscire in U come somma di alternative:
Posso uscire direttamente con probabilità (vado dritto in S1 e in S2). Oppure faccio un giro, ovvero in S2 non prendo l'uscita, ma torno in S1. Da S1 vado in S2 e poi esco; questa seconda alternativa ha probabilità
. In generale, se k è il numero di giri che faccio prima di uscire, la probabilità, funzione di k, sarà data da:
. L'uscita può avvenire dopo 1,2,3, ...k giri. Per ottenere il valore della probabilità dobbiamo sommare tutte queste alternative, ottenendo la somma di una serie.
Si ha perciò:P=. La serie è geometrica, per cui:
, e ritroviamo quindi il risultato di Gianfranco (che si è limitato a una somma finita) senza approssimazioni.
La probabilità Q invece di girare all' infinito senza uscire per U è data unicamente da:
Q=; quindi tale proprietà è nulla. Questa è una conseguenza del teorema di Bernulli, che abbiamo visto qui.
Notiamo la differenza tra P e Q; P si può ottenere come somma di infinite alternative e alla fine dà un numero finito, mentre Q si ottiene solo come un unico evento ripetuto infinite volte. Ma sappiamo che questo non è possibile, ovvero che tale evento ha probabilità nulla.






5 commenti
Riporto un'altra possibile soluzione ;-)
Detta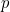 la probabilità di uscire, dal grafo precedente (non so se si vede...) si deduce la seguente equazione:
la probabilità di uscire, dal grafo precedente (non so se si vede...) si deduce la seguente equazione:
Non sono riuscito ad inserire l'immagine del grafo. Eccola.
Grazie Vincent; soluzione corretta, vedo appena posso di aggiungerla a questo articolo.
Ciao
Umberto, mi sarebbe utile se nell'aggiungere questa soluzione potessi esplicitarla maggiormente. Francamente non ho capito la relazione utilizzata. Probabilmente mi mancano delle nozioni di base sui grafi.
Fabrizio,
l'equazione è giusta.. per il resto non ci ho pensato più di tanto. il quiz è chiuso da tempo e inoltre sono cambiati gli approcci ai quiz.
Sto finendo un articolo importante, poi vedo se posso integrare la soluzione
Ciao