Questo articolo è stato inserito nella pagina d'archivio dedicata alla Relatività Ristretta e Spaziotempo di Minkowski

 

Un bel problemino relativistico (RR) che sembra portare a un paradosso. Un’attenta analisi dei fatti, però, fa rientrare tutto nelle regole… Einstein , per questa volta, si salva.

Consideriamo due astronavi A e B di lunghezza uguale (Lo). Esse viaggiano una contro l’altra lungo l’asse x, separate da una piccola differenza in y, in modo da non scontrarsi. Ciascuna vede l’altra avvicinarsi con una velocità u (Fig. 1).

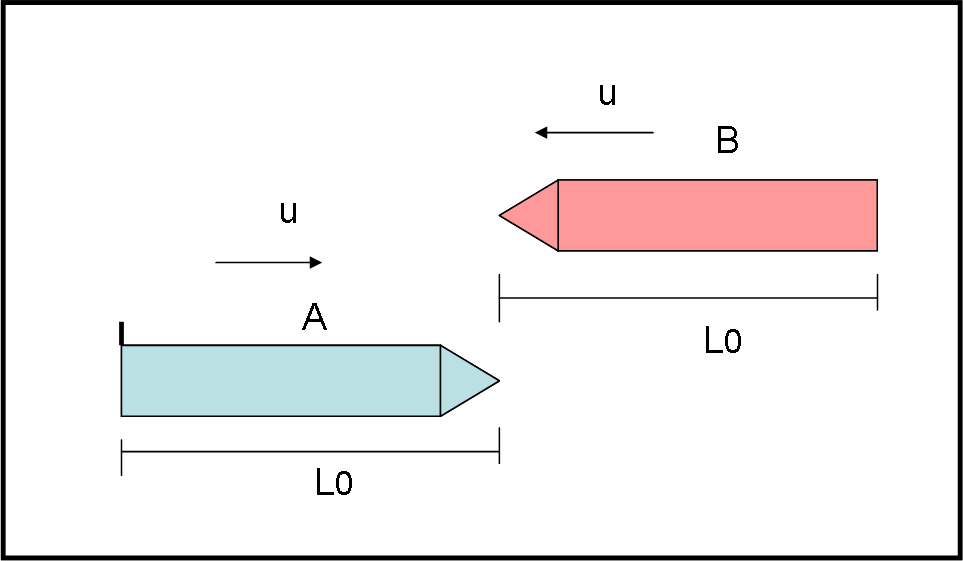
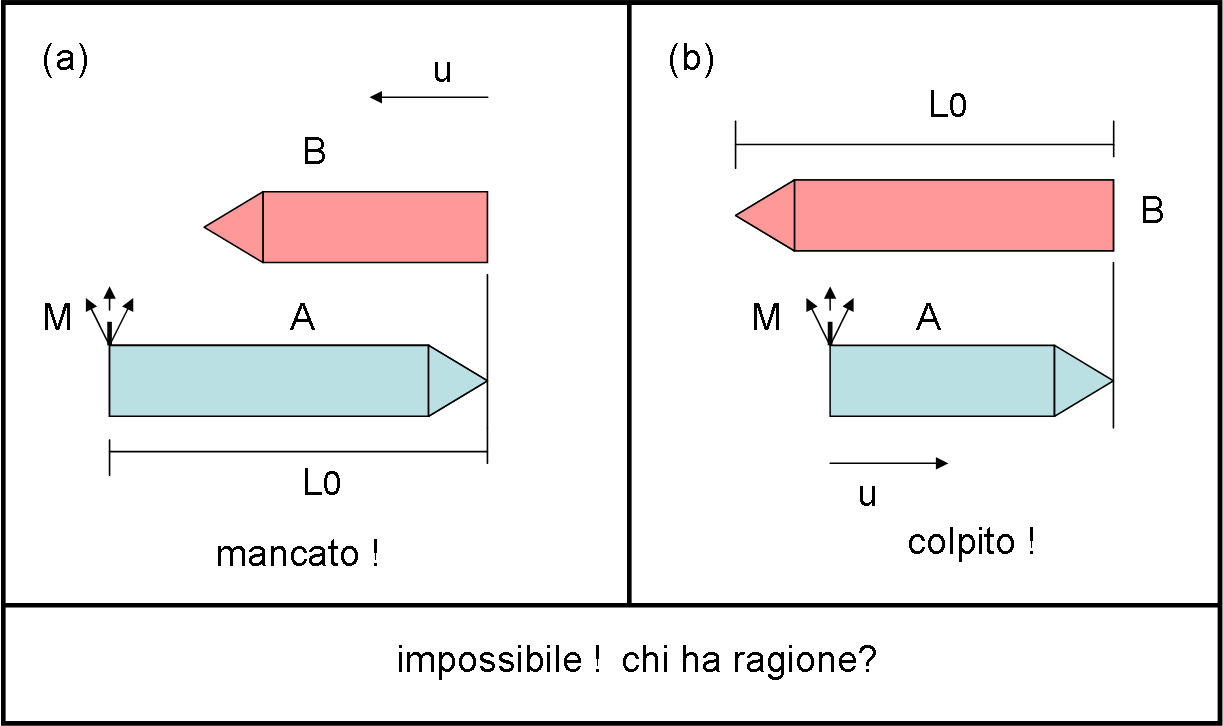
Se ci poniamo su A, quando la coda di B tocca la punta di A, un missile viene sparato dalla coda di A verso B (Fig. 2a). Ovviamente il missile andrà a vuoto, a causa della contrazione della lunghezza di B, visto da A.

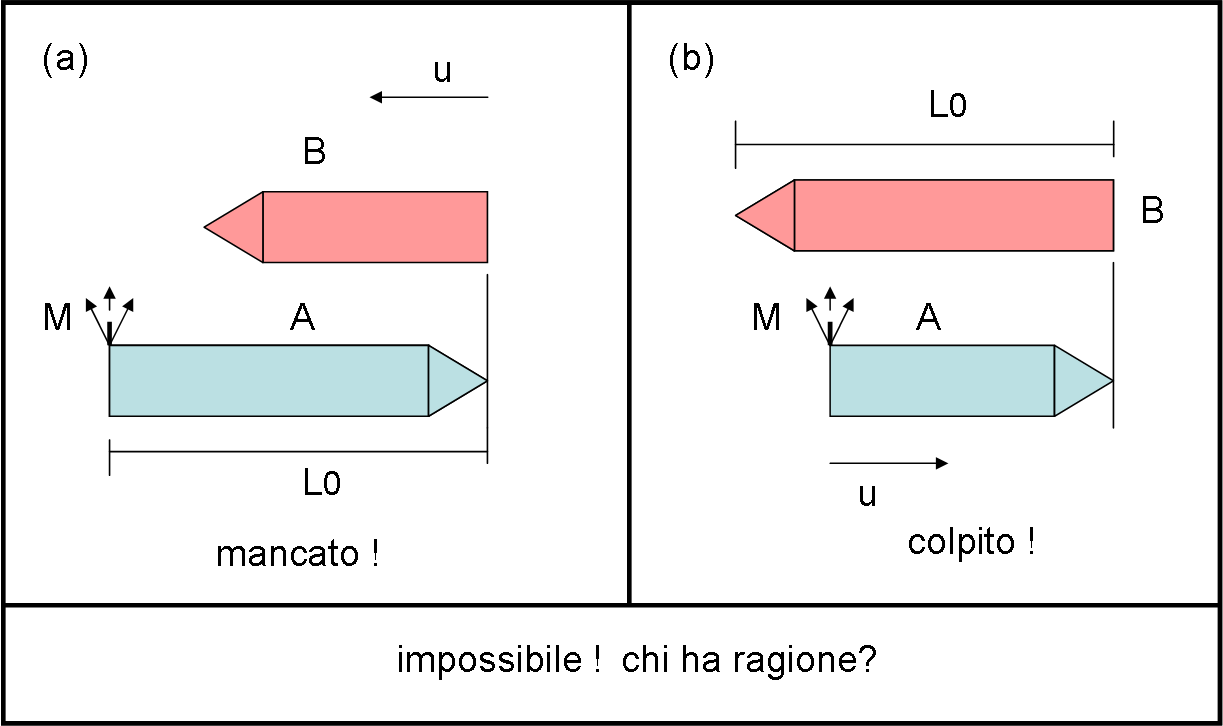
Tuttavia, se ci poniamo su B, la stessa situazione porterà a un colpo vincente del missile di A (Fig. 2b). Attenzione: poniamo uguale a zero il tempo che il missile compie per andare da A a B.

Assurdo! Siamo in relatività ristretta ed entrambi i sistemi devono vedere lo stesso fenomeno, ossia anche B deve concludere che il missile non può colpirlo o viceversa. Chi ha ragione? E perché?

Per chi vuole provare a risolverlo da solo, questo è il momento di sospendere la lettura e munirsi di carta e matita... Gli altri vadano pure avanti

Il problema si chiarisce al meglio identificando una serie di eventi E(x_A,t_A) nel sistema di A e, poi, utilizzare le trasformazioni di Lorentz per ottenere gli stessi eventi nel secondo sistema E(x_B,t_B). Bastano poi fare un po' di  confronti e ragionare...

Ovviamente, si può anche  anche rappresentare graficamente l'apparente paradosso  con Minkowski…

Il problema è sicuramente interessante ed  è uno dei tanti che sembrano portare a un paradosso della relatività ristretta. Il punto chiave è che tutto è perfettamente simmetrico, tranne il fatto che una certa azione viene eseguita, a un certo istante, da una sola delle due astronavi (ossia da uno solo dei due sistemi di riferimento). Ancora una volta, ci scontriamo con il concetto fondamentale della relatività della simultaneità (che abbiamo trattato a fondo nella spiegazione della RR).

L’astronave A spara quando succede qualcosa (simultaneità), ma la stessa simultaneità non viene vista dall’altro sistema, dove non avviene l’evento “sparo”.

L' “apparente” paradosso è simile a quelli della vita allungata del “muone” o del treno e della galleria troppo stretta (QUI e QUI). Da non confondere, quindi, con un paradosso come quello dei gemelli (di cui si parla varie volte nei due link precedenti).

L’evento fondamentale del nostro problema è lo sparo del missile da parte dell’astronave A. E’ quindi più che logico cominciare ad analizzare la situazione attraverso un osservatore solidale con A e identificare con esattezza una serie di eventi E_Ai, attraverso le loro coordinate spaziali x_Ai e temporali t_Ai.

Chiariamo subito un paio di cose: abbiamo parlato di due navi che passano vicinissime e abbiamo anche supposto che il missile parta da A e raggiunga B nello stesso momento. Questo non può essere vero, ovviamente, ma è solo una semplificazione per non complicare ulteriormente il quiz. Tuttavia, possiamo sempre pensare che le due navi striscino realmente in modo che non ci sia intervallo tra di loro o, se preferiamo, dire che siamo interessati allo sparo di A e non dare peso al vero impatto con B.

Analogamente, stiamo parlando di due eventi simultanei (la visione della coda di B e lo sparo) che avvengono all’interno di un’astronave  che ha una certa lunghezza. Il che vuol dire che per trasmettere un segnale al missile, deve passare un po’ di tempo, per breve che sia. La faccenda potrebbe anche risolversi tenendo conto della velocità finita della luce o attraverso qualche strano marchingegno che permetta realmente una perfetta simultaneità dei due eventi. In fondo abbiamo già avuto a che fare con il problema della sincronizzazione degli orologi, che non differisce più di tanto. Ammettiamo, perciò che si possa realmente guardare da un punto dell’astronave e sparare da un altro in un intervallo di tempo uguale a zero, per chi viaggia nell’astronave. Il nostro è un problema squisitamente teorico e non pratico…

Ricordiamoci, inoltre, cosa significa evento. Nello spaziotempo prende il posto del punto nello spazio. Basta aggiungere, alle tre coordinate spaziali del punto, la coordinata tempo. Un evento rimane sempre lo stesso nello spaziotempo, ma le sue coordinate possono variare da sistema di riferimento a sistema di riferimento, così come capita per un punto nello spazio.

A questo punto, possiamo cominciare a risolvere il "duello", dando per buono, però, che chi si accinge a seguirci abbia una conoscenza sufficiente dei concetti fondamentali della RR e della sua rappresentazione nel diagramma di Minkowski. Se qualcuno li ha dimenticati, è meglio che vada a rileggere gli articoli relativi negli approfondimenti riportati all'inizio.

Prendiamo come riferimento l'astronave A

Quali sono gli eventi fondamentali che caratterizzano il problema, calcolati nel sistema di riferimento di A?

Innanzitutto quando la punta dell’astronave B tocca la punta dell’astronave A. Non succede niente di speciale, ma è bene tenerla in conto come riferimento iniziale dell’intera operazione. Il secondo evento è, sicuramente, il contatto tra la coda di B e la punta di A. Questo è il momento più importante, perché è proprio quello che decide lo sparo del missile. Per l’osservatore di A lo sparo deve essere simultaneo al contatto tra punta di A e coda di B. Lo sparo è, perciò, il terzo evento. Il tempo del secondo e del terzo evento sono identici, per A, ma cambia la posizione dell’evento… (tra punta e coda dell’astronave A vi è una certa lunghezza Lo).

Attenzione: abbiamo già detto una cosa importantissima: i due eventi hanno lo stesso tempo, ma non hanno la stessa posizione spaziale. Sapendo che nella RR spazio e tempo sono legati strettamente, si può già capire che una differenza di spazio può portare a una differenza di tempo in altro sistema di riferimento. Ricordiamo, ancora, però, che la contrazione delle lunghezze e la dilatazione del tempo del sistema in movimento, vengono osservati dal sistema considerato fermo. In realtà, sia il tempo che le lunghezze sono gli stessi se misurati all’interno di qualsiasi sistema inerziale (tempo e lunghezza propria). In altre parole, gli orologi delle due astronavi segnano lo stesso tempo così come la loro lunghezza è sempre Lo.

Avvenuto lo sparo, l’osservatore di A si rende conto che qualcosa non è andata per il suo verso. Il missile ha mancato il bersaglio. Non era difficile da capire, dato che avrebbe dovuto sapere benissimo che l’astronave B, venendogli incontro con una certa velocità, si accorcia rispetto alla sua. La lunghezza Lo è diventata L, dove:

L = Lo/γ

con:

γ = 1/(1 – v²/c²)^1/2

γ è proprio il celeberrimo fattore di Lorentz.

Il fattore di Lorentz è proprio quello che accorcia le distanze e dilata i tempi in due sistemi che si muovano con velocità v costante uno rispetto all’altro.

γ è sempre maggiore di 1 (v e sempre minore di c e diversa da zero), per cui L è sempre minore di Lo (abbiamo diviso un certo numero per un numero maggiore di 1).

Questa contrazione fa sì che la punta dell’astronave B non si trovi assolutamente all’altezza della coda di A, al momento dello sparo. Deve passare del tempo prima che si verifichi questo nuovo evento, ossia quello in cui la punta di B tocchi la coda di A.

Infine, tanto per concludere in bellezza, consideriamo un ultimo evento, ossia quello in cui la coda di B tocchi la coda di A. Poi le due astronavi se se andranno per conto loro con un nulla di fatto.

Siamo in relatività ristretta e, perciò, qualsiasi fenomeno osservato in un sistema di riferimento deve anche accadere nell’altro. Se il missile di A ha “mancato” B nel sistema di A, deve mancarlo anche nel sistema di B, cosa che sembra non accadere, da cui l’apparente paradosso.

Questa contraddizione si vede molto bene se raffiguriamo le situazioni nei due sistemi, come fatto nella Fig. 2, che riportiamo per comodità.  La figura, però, non tiene conto degli effettivi istanti dei vari eventi.

Cominciamo, perciò, a calcolare, prima, gli eventi descritti nel sistema A, inserendoli con tempo crescente.  Aiutiamoci con la Fig. 3. dove le x positive vanno verso destra e il tempo verso l’alto. Chiamiamo le ascisse x_A e i tempi t_A, dato che corrispondono al sistema A. L’astronave A sarà, d’ora in poi, disegnata in verde. La B sarà disegnata in rosso.

Il primo evento dice: la punta di A tocca la punta di B. Mettiamo l’origine degli assi proprio in questo punto di contatto e facciamo partire l’orologio in questo preciso istante. Ne segue che le coordinate spaziotemporali  di questo evento per l’astronave A sono x_A1 = 0 e t_A1 = 0. In breve:

E_A1 = (0.0)

Vista dall’astronave A, l’astronave B ha una velocità – u.

Sappiamo anche che la velocità u è data da

u = x_A/t_A

Ossia:

t_A = x_A/u

Ne segue che, conoscendo le ascisse (spazio) è estremamente facile calcolare i tempi di percorrenza.

Il secondo evento E_A2 (contatto tra la punta dell’astronave A e la coda dell’astronave B) avviene dove l’ascissa x_A2 è ancora 0, ma il tempo passato è legato allo spazio percorso con un certa velocità. Dato che la distanza tra la punta e la coda di B è uguale alla lunghezza “contratta” L di B, affinché l’astronave percorra questa distanza deve passare un certo tempo, dato da:

t_A2 = - L/- u

Ricordando che:

L = Lo/γ

t_A2 = Lo/(γu)

Cerchiamo di capire bene questo passaggio… L’evento E_A2 avviene in un certo punto, ma quando tutta l’astronave B (di lunghezza contratta) è passata dal punto O. Infatti, nel punto O si trova adesso la coda dell’astronave B. Il tempo passato (t_A2 – 0), non è altro che lo spazio percorso diviso per la velocità. Lo spazio percorso non è altro che – L (in verso opposto al senso positivo delle x), mentre la velocità è – u.

Ne segue che

E_A2 = (0, Lo/(γu))

Nello stesso istante (t_A2), però, l’astronave A fa fuoco con il missile, che si trova in coda. Questo evento E_A3, per l’astronave A, avviene allo stesso tempo di E_A2, ma a una distanza – Lo (distanza tra coda e punta di A, ossia  x_A2 = - Lo – 0 = - Lo). Abbiamo, perciò:

E_A3 = (- Lo, Lo/(γu))

Interessante è anche l’evento successivo EA4, ossia quello che corrisponde al tocco della coda di A da parte della punta di B.

Qual è l’ascissa di questo evento. Beh, facilissimo: la stessa del missile (che si trova proprio in coda), ossia x_A3 = x_A2 = - Lo. Quanto tempo è passato dall’inizio dell’avventura? Niente di più facile… il tempo impiegato dalla punta di B a passare dall’ascissa 0 all’ascissa – Lo, ossia:

t_A4 = -Lo/-u = Lo/u

da cui

E_A4 = (- Lo, Lo/u)

Concludiamo con l’evento E_A5. Il luogo dove avviene ha sempre ascissa – Lo (ove si trova la coda i A). Il tempo, invece, è quello precedente, al quale dobbiamo, però, aggiungere quello necessario perché la coda dell’astronave B arrivi a toccare la coda di A. In altre parole, aggiungere il tempo necessario a far spostare la coda di B della lunghezza contratta L.

Ossia:

t_A5 = t_A4 + L/u = Lo/u + L/u = Lo/u + Lo/(γu)

da cui:

E_A5 = (- Lo, Lo/u + Lo/(γu))

Bene, abbiamo descritto numericamente tutti gli eventi.

Riscriviamoli mettendoli in colonna:

E_A1 = (0, 0)

E_A2 = (0, Lo/(γu))

E_A3 = (- Lo, Lo/(γu))

E_A4 = (- Lo, Lo/u)

E_A5 = (- Lo, Lo/u + Lo/(γu))

Lasciamo pure da parte (per un attimo) le x che ci servono per identificare DOVE capita l’evento, e controlliamo i tempi dei vari eventi. Il primo è 0. Il secondo avviene a un tempo leggermente più grande. Nello stesso istante avviene anche il lancio del missile. Perfetto! Poi a un tempo leggermente maggiore (Lo/u > Lo/(γu), dato che γ é maggiore di 1) si ha il quarto evento e infine a un tempo ancora più lungo si ha l’ultimo evento.

Finora, direi che non abbiamo avuto alcun problema e le varie configurazioni sono descritte dalla Fig. 3. Notate che nella figura abbiamo anche scritto C (coda) e P (punta) a colori per identificare immediatamente i punti delle astronavi che vengono a contatto.

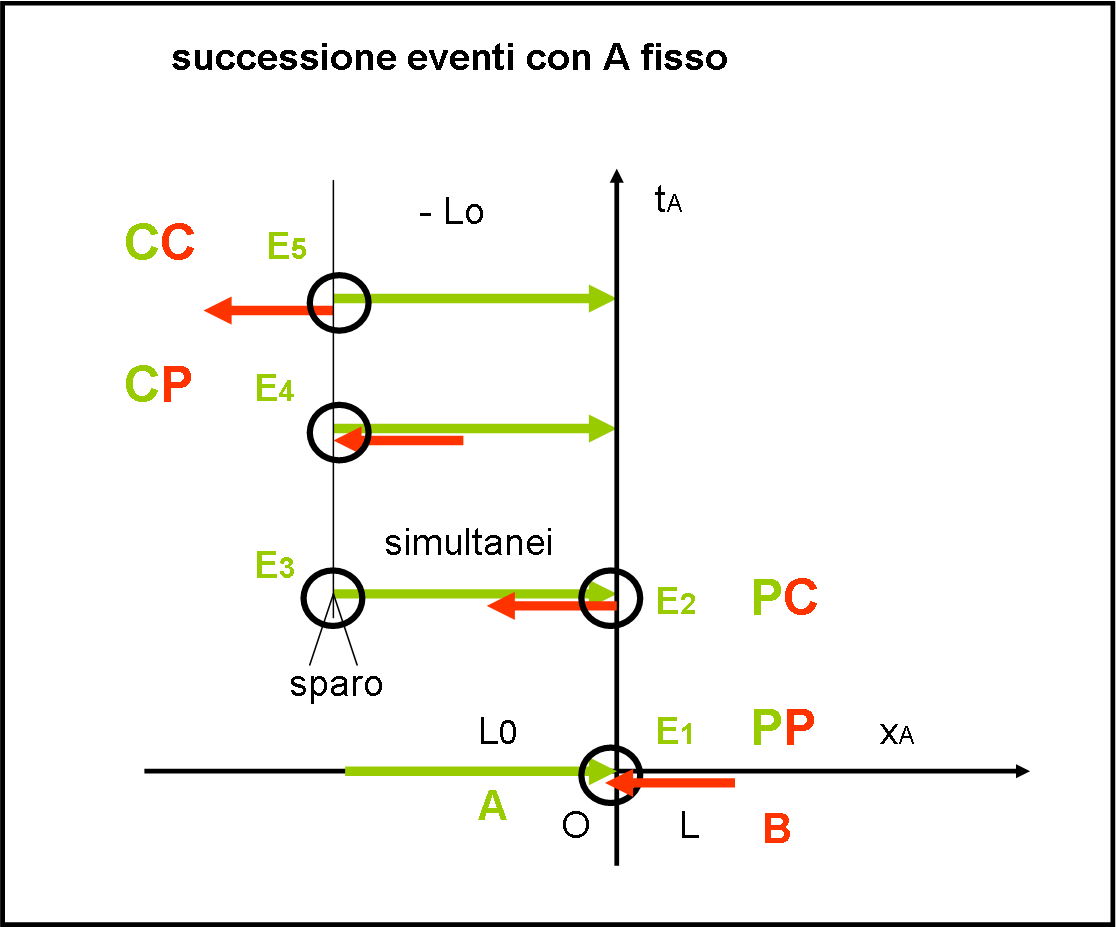
In particolare, però, ci interessa un confronto tra due eventi, il quarto e il terzo. Esso ci dice chiaramente che il missile sparato da A manca l’astronave B, dato che il tempo dello sparo (evento E₃) è minore di quello dell’arrivo dell’astronave B nel luogo del missile (evento E₄):

t_A3 = Lo/(γu) < t_A4 = Lo/u

Questo confronto è quello che decide in modo decisivo il fallimento dello sparo. Se il missile viene sparato PRIMA che la punta di B raggiunga la coda di A, siamo sicuri che non farà nessun danno.

Teniamo presente questa constatazione che ci servirà moltissimo quando passeremo a considerare fermo il sistema dell’astronave B.

Anzi, lo facciamo subito. Attenzione, però. Non ci cureremo assolutamente della visione grafica (lo faremo dopo), ma solo e soltanto della trasformazione di Lorentz, quella che ci permette di calcolare lunghezze e tempi in un sistema in movimento uniforme rispetto al primo.

Prendiamo come riferimento l'astronave B

Consideriamo, perciò, B come sistema fisso e vediamo come lui calcola le coordinate degli stessi eventi, introdotti precedentemente. Ricordiamoci bene, infatti, che le coordinate possono cambiare, ma gli eventi rimangono gli stessi.

Scrivendo le formule di trasformazione ci accorgiamo subito perché abbiamo calcolato anche le ascisse: nella relatività ristretta il tempo e lo spazio sono legati assieme in modo indissolubile!

La trasformazione di Lorentz si scrive, in generale:

x’ = γ(x - v t)

t’ =  γ(t - v x/c²)

Dove v è la velocità con cui si muove il sistema S’ rispetto a S.

Nel nostro caso S’ è il sistema di B e S è il sistema di A. La velocità con cui si muove B rispetto ad A è - u, per cui la trasformazione diventa:

x_B = γ(x_A + u t_A)

 t_B = γ(t_A + (u/c²) x_A)

Applichiamola a ogni evento

E_B1 = (0, 0)

Questo risulta ovvio, dato che x_A =  0 e  t_A = 0.

Passiamo a calcolare le coordinate del secondo evento:

x_B2 = γ (0 + u Lo/γu) = Lo

t_B2 = γ (Lo/γu + (u/c²) 0) = Lo/u

E_B2 = (Lo, Lo/u)

E’ il momento del terzo, un punto fondamentale, dato che è quello in cui viene sparato il missile. Non ditemi, però, che deve essere un evento simultaneo a quello precedente! Dato che l’ascissa tra i due eventi è diversa, la trasformazione porta a tempi diversi… Pensiamoci bene… la simultaneità è relativa al sistema di riferimento!

x_B3 = γ(- Lo + u Lo/(γu)) =  - γ Lo + uγLo/(γ u) =  Lo – γ Lo

t_B3 = γ(Lo/(γu) - (u/c²) Lo) = Lo/u – γuLo/c²

E_B3  = (Lo – γ Lo, Lo/u – γuLo/c²)

Altrettanto importante è il quarto evento, quello che, in pratica, decide se il missile va a vuoto oppure no. Siamo, infatti, arrivati all’evento che  descrive quando la coda di A tocca la punta di B. Un missile lanciato prima di questo evento NON può colpire l’astronave B, dato che B non ha ancora raggiunto il punto del lancia missili di A. Ricordiamoci, sempre, che gli eventi trattati nei due sistemi sono gli stessi! Cambiano solo le loro coordinate…

x_B4 = γ(- Lo + uLo/u) = 0

t_B4 = γ(Lo/u – uLo/c² )

Mettiamo in evidenza γ (Lo/u ):

t_B4  = γ (Lo/u )(1 – u²/c²)      …. (1)

Ricordando che

γ  = 1/(1 – u²/c²)^1/2

ossia:

γ²  = 1/(1 – u²/c²)

 1 – u²/c² = 1/γ²

Sostituendo nella (1), si ottiene:

t_B4= γ (Lo/u) ∙ (1/γ²) = Lo/(γu)

E_B4 = (0, Lo/(γu))

Concludiamo con il quinto evento:

x_B5 = γ(- Lo + u (Lo/u + Lo/(γu))) = γ(- Lo + u Lo/u + uLo/(γu))) = γ (uLo/(γu)) = Lo

t_B5 = γ(Lo/u + Lo/(γu) - (u/c²)Lo) =  γ Lo/u(1 – u²/c²) + γ Lo/(γu) = Lo/uγ + Lo/u

E_B5 = (Lo, Lo/uγ + Lo/u)

Confrontiamo gli eventi

Bene. Non ci resta che confrontare gli eventi espressi con le coordinate del primo sistema e quelli espressi con le coordinate del secondo sistema. Gli eventi sono gli stessi, ma non è affatto detto che lo siano le coordinate che li rappresentano, soprattutto quelle temporali…

E_A1 = (0, 0)                                          E_B1 = (0, 0)

E_A2 = (0, Lo/(γu))                              E_B2 = (Lo, Lo/u)

E_A3 = (- Lo, Lo/(γu))                    E_B3 = (Lo – γ Lo, Lo/u – γuLo/c²)

E_A4 = (- Lo, Lo/u)                          E_B4 = (0, Lo/(γu))

E_A5 = (- Lo, Lo/u + Lo/(γu))             E_B5 = (Lo, Lo/(uγ) + Lo/u)

Proviamo a inserire, in Fig. 4, gli eventi nello stesso ordine di pima (da E₁ a E₅), come fatto in Fig. 3. Facendo questo, cosa ammetteremmo? Ammetteremmo che la simultaneità rimanga la stessa cambiando sistema. E questo sappiamo bene che nella RR  non funziona.

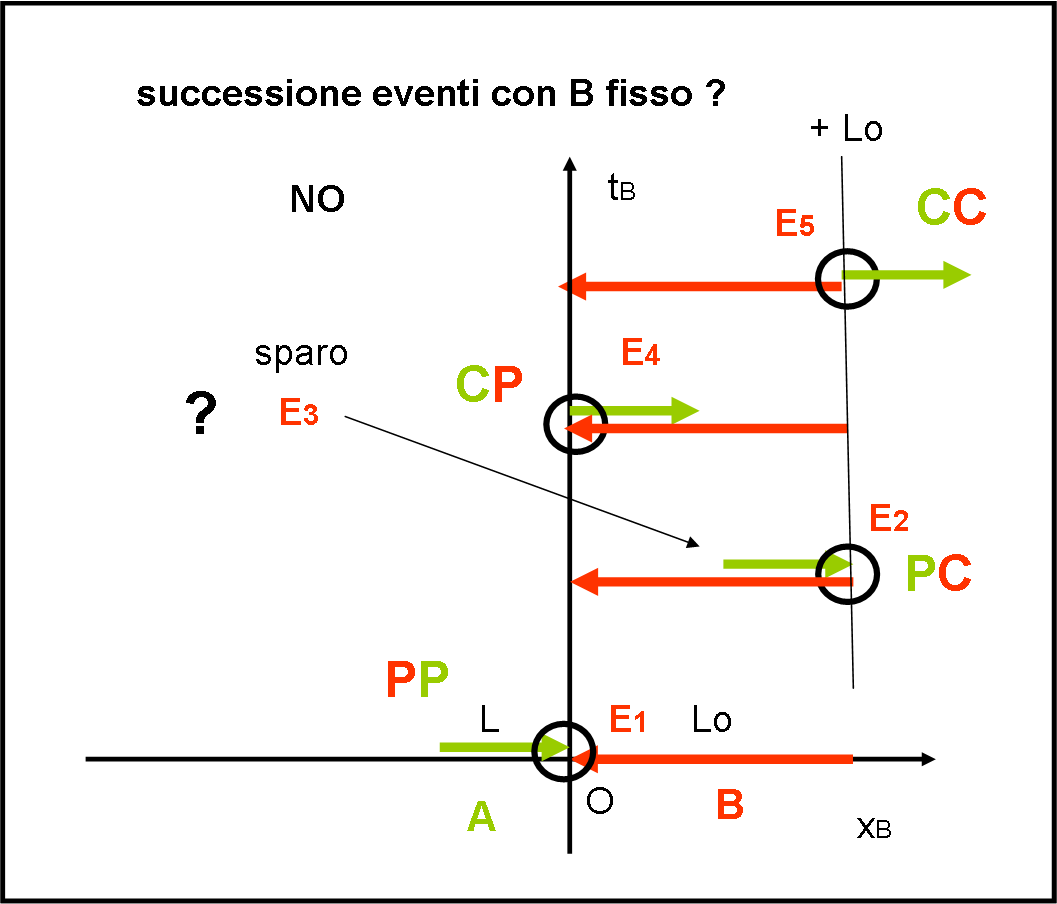
Come volevasi dimostrare… mamma mia che pasticcio!

Risulta evidente che i tempi non sono più rispettati. Ad esempio, E_B4 deve essere avvenuto prima di E_B2 (come fa la freccia verde a colpire la coda di B prima di entrare in B ?). Non è certo difficile verificarlo direttamente confrontando i tempi degli eventi calcolati nel sistema rosso di B.

Confrontiamo t_B2 e t_B4.

t_B2 = Lo/u

t_B4 = Lo/(uγ)

Ossia.

t_B4 = t_B2/γ

Ma, sappiamo che γ è sempre maggiore di 1 e quindi ne segue che:

t_B4 < t_B2.

Proprio come ci faceva già capire la Fig. 4.…

E poi… dove andiamo a inserire l’evento E_B3, quello dello sparo? Un ragionamento sbagliato ci farebbe pensare che debba avvenire contemporaneamente a E_B2 (punta di A che tocca la coda di B). Così ragionando, cadremmo in uno sparo disastroso e nel paradosso

Tuttavia, se è capitato che E_B2 ed E_B4 si sono scambiati la posizione temporale, chissà mai che non succeda anche a E_B3. Magari va proprio a finire che lo sparo avvenga prima che la coda di A entri dentro l’astronave rossa, ossia prima di E_B4…

Andiamo subito a controllare i nuovi tempi calcolati prima e, in particolare, i tempi t_B4 e  t_B3.

Prima di procedere, notiamo un altro fatto interessante, ma ovvio: la fine e  l’inizio dell’avventura, hanno le stesse coordinate temporali in entrambi i sistemi.

t_A1 = t_B1 = 0

t_A5 = t_B5 = Lo/(uγ) +  Lo/u

Riassumiamo anche la situazione:

L’ordine temporale nel sistema di B ha, per il momento, la seguente sequenza: E_B1, E_B4, E_B2, E_B5. Non ci rimane che piazzare E_B3, corrispondente al momento del lancio del missile. La sua posizione è molto importante. Se dovesse inserirsi prima di E_B4 vorrebbe dire che il lancio del missile avverrebbe prima che la punta di B tocchi la coda di A e quindi anche in questo caso l’astronave B non verrebbe colpita. Essa, infatti, sarebbe colpita solo per tempi maggiori di t_B4.

In poche parole vogliamo (e dobbiamo, altrimenti chi lo sente Einstein?) trovare che:

t_B3 < t_B4

ossia:

Lo/u – γuLo/c² < Lo/(γu)

Forza e coraggio… non è poi così difficile.

Scriviamola, mettendo in evidenza  Lo/(γu) nel primo membro:

Lo/(γu)(γ – γ²u²/c²) < Lo/(γu)

In altre parole, bisogna dimostrare che

(γ – γ²u²/c²) < 1

Esplicitando γ, si ottiene:

1/(1 – u²/c²)^1/2 – 1/(1 – u²/c²) (u²/c²) < 1

Poniamo:

β = u/c

Abbiamo

1/(1 – β²)^1/2 – β²/(1 – β²) < 1

((1 – β²)^1/2 – β²)/(1 – β²) < 1

((1 – β²)^1/2 – β²) < 1 – β²

(1 – β²)^1/2 – β² < 1 – β²

(1 – β²)^1/2 < 1

1 < 1/(1 – β²)^1/2 = γ

Ossia:

γ > 1

Il che è sempre vero (e lo abbiamo ribadito anche all’inizio dell’articolo)… magnifico!

Abbiamo dimostrato che l’evento E_B3 avviene prima di E_B4, ossia, detto in parole spicce, il missile viene sparato da A prima che la coda di A (dove è piazzato il lancia missili) sia passata dalla testa di B. Il colpo va a vuoto!

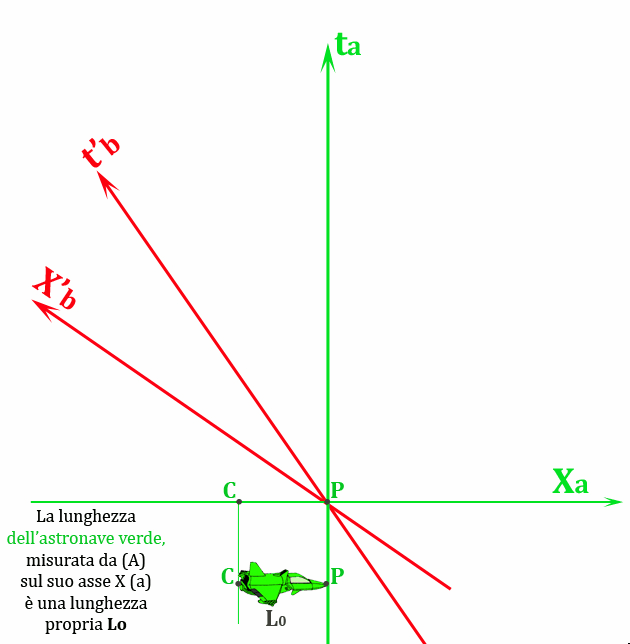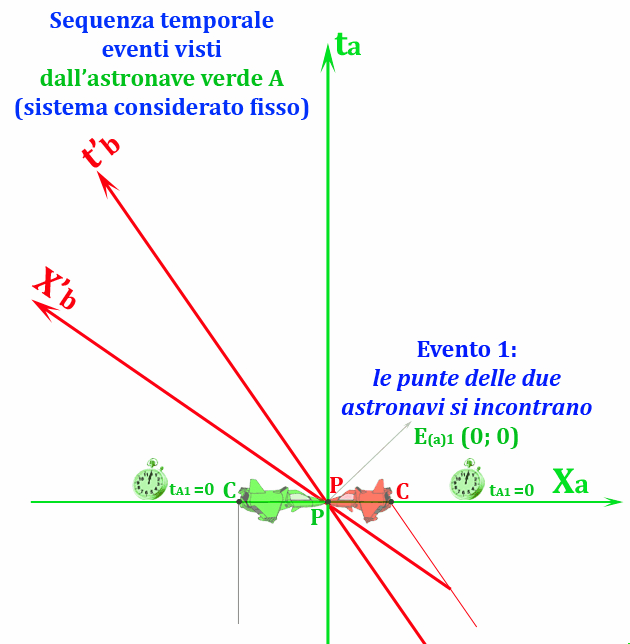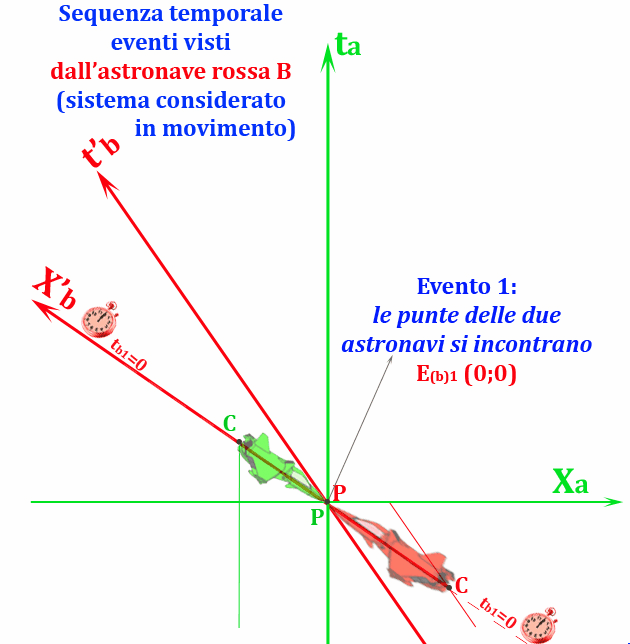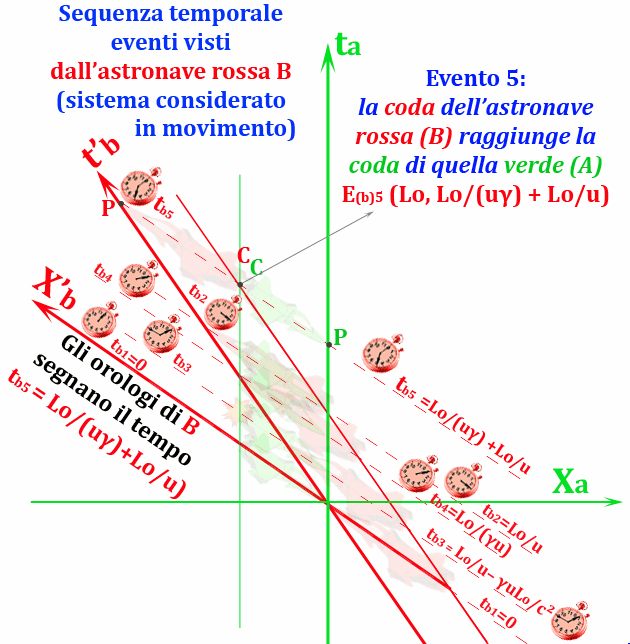
La sequenza temporale degli eventi visti da B è:

E_B1, E_B3, E_B4, E_B2, E_B5, come  rappresentato nella Fig. 5.

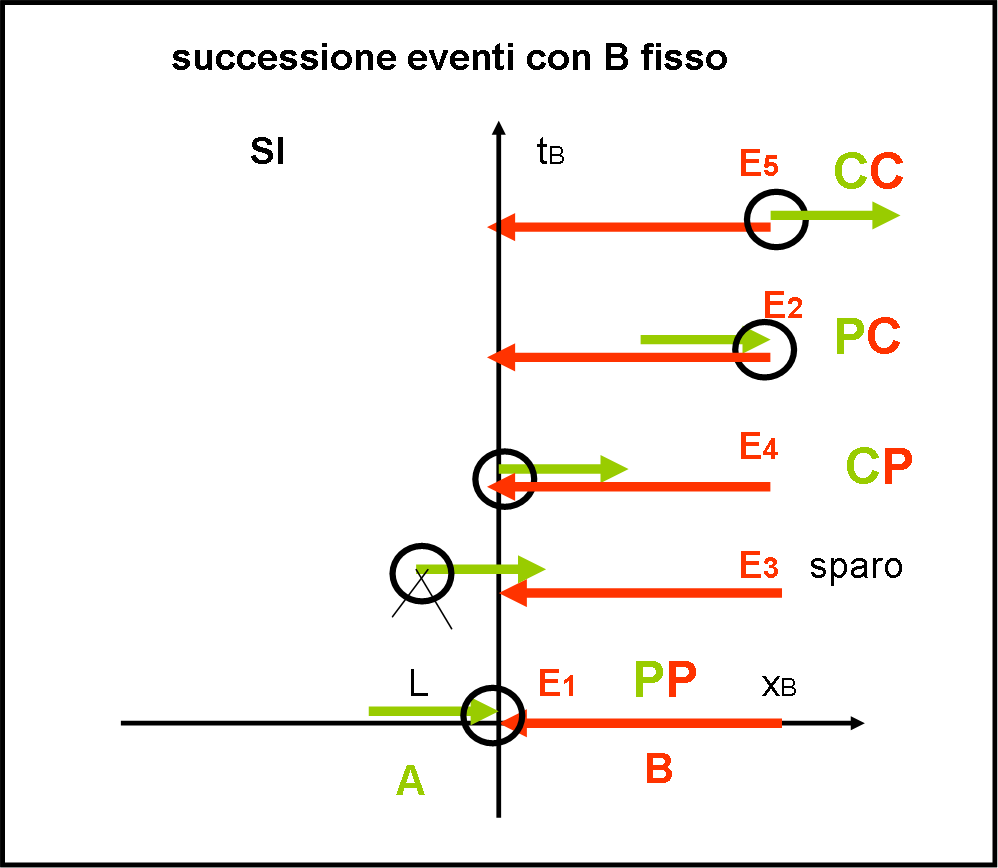
Quando si dice che la relatività ristretta si basa, innanzitutto, sulla relatività della simultaneità, non si scherza mica? Non per niente è uno dei concetti su cui abbiamo “picchiato” di più…

Usiamo Minkowski

A questo punto, potremmo dire di avere risolto il paradosso e di avere fatto un bel ripasso dei concetti base della RR. Era proprio necessario usare tante formule o si poteva risolvere velocemente per via grafica? Sicuramente Sì.

Abbiamo o non abbiamo descritto con grande attenzione il digramma di Minkowski? Utilizzando lui è praticamente immediato vedere cosa succede nei due sistemi. Tuttavia, questo articolo vuole essere estremamente didattico e vogliamo disegnare il diagramma di Minkowski proprio utilizzando gli eventi calcolati precedentemente. Penso che, in questo modo, tutti i dubbi possano venire chiariti.

Non vogliamo certo introdurre di nuovo il diagramma di Minkowski (basta andare QUI), a parte un punto estremamente importante per la nostra trattazione: la contrazione delle lunghezze espressa per via grafica.

Essa ci permette di tracciare in modo approssimato la lunghezza propria Lo in qualsiasi sistema di riferimento. Utilizziamo proprio la Fig. 6 (tratta dall’articolo su Minkowski). La curva di calibrazione orizzontale ci permette di determinare l’unità di lunghezza per varie velocità. Ammettiamo che l’unità sia proprio Lo = 1. Si vede bene che “graficamente” la lunghezza Lo’ =1 sembra essere più lunga di Lo. Questo non è vero! esse sono uguali nei rispettivi sistemi (entrambe sono le unità, toccando la curva di calibrazione).

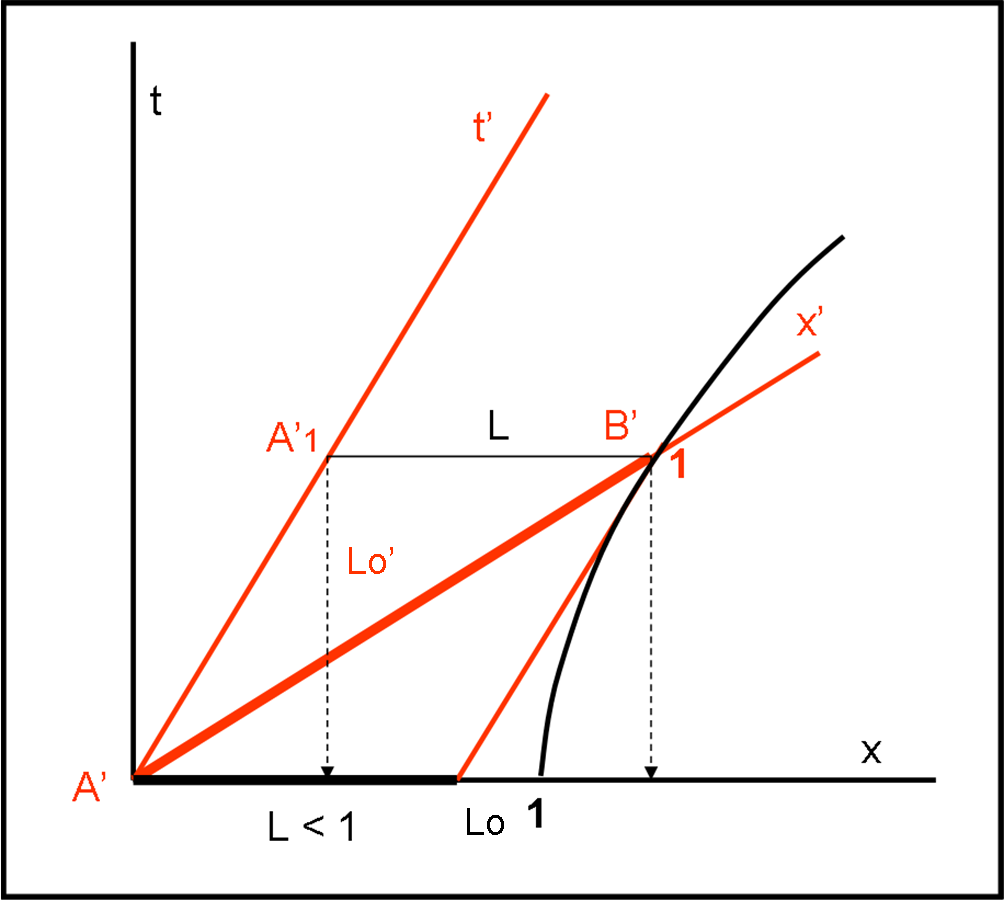
Se, invece vogliamo vedere la lunghezza L di Lo’, nel sistema fermo, dobbiamo misurare la sua proiezione lungo l’asse x. Otteniamo così la lunghezza che appare contratta nel sistema fisso.

Ciò che facciamo, adesso, è scegliere una velocità relativa qualsiasi e di considerare una certa contrazione di lunghezza senza fare i conti giusti. Le cose non cambiano e il concetto si capisce benissimo…

Consideriamo la Fig. 7, in cui il sistema A (verde) è fermo, e vediamo cosa succede all’astronave rossa B che viaggia a velocità – u verso di A. Le linee rosse sono quelle corrispondenti al tempo e allo spazio del sistema B in movimento. Le linee verdi sono le linee di tempo e di spazio relative al sistema fermo di A.

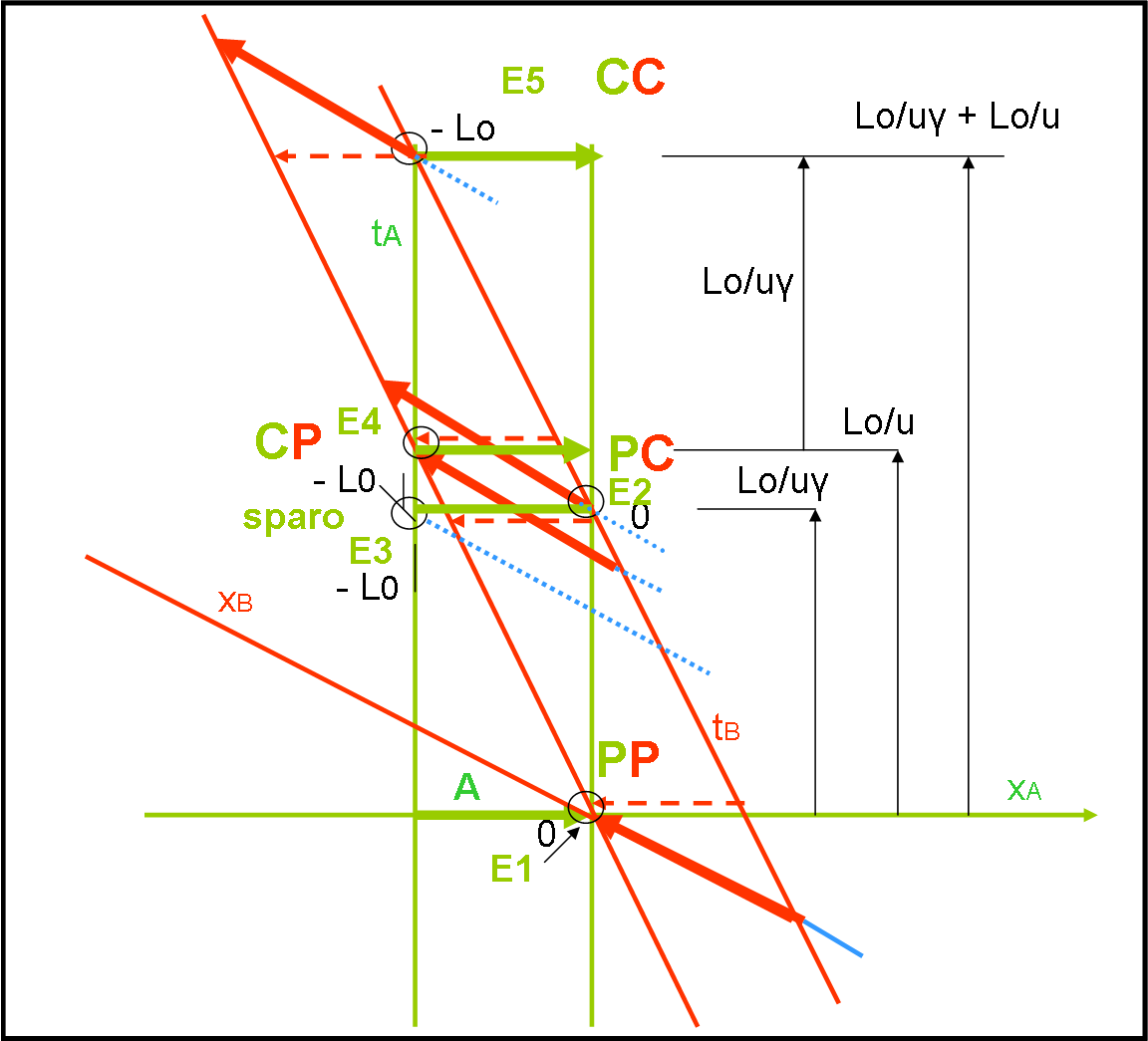
Al tempo t_A = 0 le due punte delle astronavi si toccano. Questo è il primo evento che abbiamo considerato. Le sue coordinate sono (0,0). Notiamo che A vede l’astronave B contratta lungo la sua linea spaziale (ossia quella della sua simultaneità). Questo ci dice subito che la simultaneità per il sistema verde (orizzontale) è diversa da quella del sistema rosso (inclinato).

L’astronave rossa si muove, compresa sempre tra le due linee che rappresentano la sua punta e la sua coda. Arriviamo al secondo evento, ossia quello in cui la punta di A tocca la coda di B. Immediatamente il missile viene sparato. L’evento E₃ è simultaneo all’evento E₂ e il missile va a vuoto perché l’astronave B viene vista contratta (linea tratteggiata rossa). E₃ ed E₂ stanno sulla stessa linea orizzontale, dato che sono simultanei nel sistema verde.

L’astronave rossa continua  e giungiamo all’evento E₄, quello in cui la punta di B tocca la coda di A. Tutto bene. Infine, ecco l’evento E₅ in cui le due astronavi sono coda contro coda.

Vicino agli eventi e a destra del grafico ci sono le lunghezze e i tempi misurati nel sistema di A. Esattamente quelli che abbiamo calcolato precedentemente.

Quello che vogliamo fare, adesso, è ribaltare la situazione, considerare B fisso e studiare come si muove A rispetto al sistema di B.

Nella Fig. 7 sono state tracciate delle linee puntinate azzurre… Esse corrispondono proprio ai tempi che andremo a calcolare. In pratica, non ci sarebbe bisogno di rifare la figura. Ma è meglio abbondare con i passaggi e, magari, dopo tornare alla Fig. 6 e capire meglio il concetto.

Disegniamo la Fig. 8, in cui l’astronave B è ferma e si muove la A.

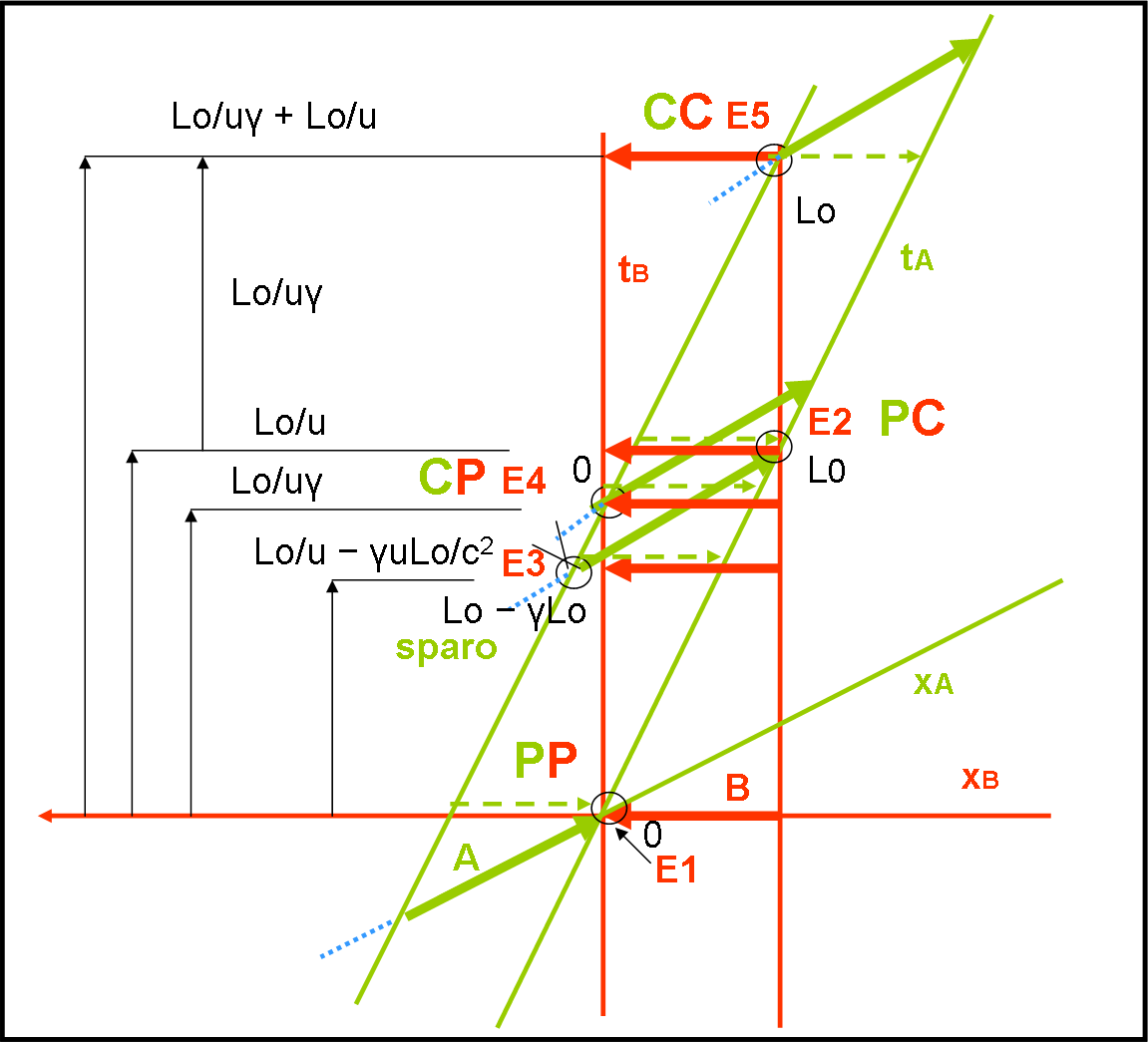
Si vede chiaramente che la linea di simultaneità di A è adesso ben diversa dalla linea orizzontale. In particolare, dire che quando la punta di A tocca la coda di B (evento E₂), si deve sparare simultaneamente il missile (evento E₃), vuol dire  anticipare di molto l’evento sparo (E₃) rispetto al punta-coda (E₂), nel sistema di riferimento rosso, che è quello che adesso misura la simultaneità in orizzontale. Analogamente si vede che E₄ (la punta di B viene raggiunta dalla coda di A) avviene dopo E₃ (dalla coda di A si spara il missile) e prima di E₂. Insomma, si ritorna a quanto trovato matematicamente (e ci mancherebbe altro!).

A questo punto si può tornare a vedere la Fig. 7 e si capisce subito che le linee azzurre puntinate rappresentavano proprio i tempi misurati nel sistema B. Così come le linee azzurre  puntinate della Fig. 8 rappresentano i tempi del sistema di A.

Insomma, bastava una sola figura, ma è sempre meglio esagerare con le spiegazioni.

Consiglio di guardare attentamente le figure e cercare di comprendere ogni linea e punto. Capire questo problema vuol dire fare un grosso passo avanti nella comprensione della RR.

Riflettiamo e cominciamo a pensare al "mollusco"...

Riflettiamo, poi, su parole come “contrazione” e “rallentamento”. Le usiamo tranquillamente… ma sono reali o sono illusioni? Basta pensare al muone… Una volta che lo rileviamo ben più in basso del previsto è indubbio che il suo piccolo orologio invisibile (il suo infinitesimo battito del cuoricino) vada VERAMENTE più piano del nostro. E’ un dato di fatto. Se poi riuscissimo a farci piccoli, piccoli, eliminando tutta la nostra ciccia (ops… massa) e fossimo portati in alto nell’atmosfera e riuscissimo a prendere un muone  “al volo”, non vedremmo probabilmente il suo orologio, ma il nostro andrebbe come il suo. Ancora, più esaltante sarebbe il fatto che vedremmo la Terra venirci incontro in modo mostruosamente rapido. La distanza tra atmosfera e terreno si sarebbe SICURAMENTE accorciata.

Il vero guaio è che nessuno di noi e nessuna nostra tecnologia è in grado di raggiungere le velocità del muone e quindi certi concetti rimangono a bagnomaria tra illusione e realtà.  Quando affrontiamo il problema muone ci dimentichiamo, spesso, due parti fondamentali delle quattro che avvengono nell’avventura. Noi confrontiamo il nostro orologio con quello biologico del muone (riusciamo a farlo), ma non siamo capaci di misurare se il muone si è accorciato oppure no. Il muone si è accorto che la distanza dalla Terra si è contratta, ma non è riuscito a confrontare il suo orologio con il nostro per dirci che gli sembravamo veramente più giovani e pimpanti rispetto a lui… Per valutare una vera simmetria, bisogna valutare tutte le sue componenti… La RR non scherza…

Inoltre, per cercare veramente di capire fino in fondo bisognerebbe vivere realmente nel diagramma di Minkowski, uno strano mondo dove quello che sembra uguale non lo è e quello che sembra diverso è invece uguale. Basti pensare all’uguaglianza di tutti quei piccoli segmenti che partono dall’origine e arrivano fino alla curva di calibrazione. Si arriva perfino a stabilire che l’unità potrebbe diventare l’infinito per un fotone qualsiasi. E tutto ciò che capita al tempo è dovuto a una deformazione dello spazio e viceversa. Una “contrazione”, quindi, diventa reale nel mondo di Minkowski, ma il mondo di Minkowski è, in fondo, il nostro mondo, basta sapere da dove e come guardare.

Peccato che lo possano girare in lungo e in largo solo le particelle più piccole. La nostra massa non ci permette di goderci veramente i giochi di prestigio che avvengono costantemente nello spaziotempo. Possiamo solo fare quiz e illuderci che possano accadere.

E pensare che è ancora qualcosa di concettualmente “vuoto”, dove tutto si può muovere senza intoppi. Immaginatevi, quando il vuoto diventerà un qualcosa di concreto, di deformabile, di allungabile o accorciabile, al pari di un’ameba o di un mollusco. Sì, proprio il mollusco di Einstein, il paragone che Albert userà per descrivere come lo spazio vuoto in cui si propagavano le “forze” di Newton è invece un corpo unico che spinge, tira, accorcia e allunga a seconda di un qualcosa che conosciamo molto bene, la materia stessa e –ancor meglio- la sua densità. Campo gravitazionale uguale a Spaziotempo. Spaziotempo uguale a massa/energia. Sì, cari amici siamo in balia di un mollusco in continuo movimento che ci fa girare come una trottola. Va bene, adesso sto esagerando e mi fermo…

Conclusioni

Scusate questa divagazione che può sembrare buttata lì… ma tutto serve per prepararci al passo decisivo di quella mente “assurda” che è riuscita a pensare un qualcosa di ancora più “assurdo”, ma mai così “reale” nella storia della Scienza, ossia la RG!

Va bene, per questa volta è andata bene e abbiamo scongiurato una guerra stellare!

Abbiamo voluto trattare l’argomento in modo estremamente didattico, a volte ridondante, ma ormai sapete che preferiamo annoiare piuttosto che lasciare interdetti.

Di seguito un riassunto finale, preparato attraverso splendide animazioni, dal nostro Paolo, vero mago delle immagini.

 

Per avere un'idea delle discussioni sollevate, dei commenti e di una applicazione numerica potete andare QUI  e QUI