Questo articolo fa parte della serie "Dante - Riemann - Einstein: Dio e il Big Bang" che è stata inserita nelle sezioni d'archivio "Cosmologia" e "Arte, letteratura e storia della scienza"

 

Questo articolo compie il terzo passo verso una rappresentazione sufficientemente comprensibile dell'aspetto di una 3-sfera (immersa in un 4-spazio) in un 3-spazio, cercando sempre la massima semplicità (gli asterischi sono sempre due!). Ci troveremo di fronte l'Universo di Einstein e quello, ben più antico, di Dante Alighieri. L'inizio di una nuova avventura...

"Non è la linea retta che mi attrae, dura, inflessibile, creata dall'uomo. Quello che mi attira è la linea curva, libera e sensuale. La linea curva che ritrovo nelle montagne del mio paese, nel corso sinuoso dei suoi fiumi, nelle nuvole del cielo e nelle onde del mare. L'universo intero è fatto di curve. L'universo curvo di Einstein " (Oscar Niemeyer)

Il nostro bacherozzo a due dimensioni viene portato a sua insaputa sopra una 2-sfera, proprio quella che noi conosciamo come superficie sferica. Noi sappiamo anche che essa è immersa in un 3-spazio, ma il bacherozzo può solo muoversi su di essa e quindi non può fare altro che considerarla come un "normale" 2-spazio, ossia un piano dove vale la geometria euclidea (come, del resto, facciamo noi uomini che viviamo sulla superficie curva della Terra).

In realtà, muovendosi un po’ attorno, tutto sembra funzionare perfettamente. Non ha nemmeno difficoltà a dirigersi lungo una retta di quello spazio. Basta, infatti, che misuri la distanza minima tra due punti e il segmento così trovato si prolunga lungo una retta. E’ sempre meglio essere sicuri dei propri passi in un mondo tutto da scoprire... (la minima distanza tra due punti indica la linea retta anche su una superficie sferica come mostrato in Fig. 12. La rette sono i cerchi massimi).

Non è nemmeno difficile tracciare un’altra retta perpendicolare alla prima (misurare gli angoli è una sua specialità). Perché fa tutto ciò? Il motivo è semplice: deve costruirsi una casetta tranquilla e nel suo mondo gli basta solo un bel quadrato segnato da quattro righe ben marcate per terra. Tutti capiranno che è casa sua e nessuno verrà a disturbarlo. Questo è il mondo dei bacherozzi: semplice e ordinato!

Vediamo le sue manovre in Fig.13.

Parte da O (punto intersezione delle due rette) e segna sulle due rette i punti A e B tali che la distanza OA sia uguale a quella OB. Questo sarà il lato della sua casetta-quadrata. Non gli resta che tracciare da A e da B due nuove rette, perpendicolari a quelle di partenza, ed esse  non possono che incontrarsi in C. La casetta è pronta. Verifica ancora che gli angoli in A, O e B siano retti e si sistema per fare una dormitina.

Però, però, c’è qualcosa che non va… non riesce a prendere sonno. Lui è un bacherozzo veramente sensibile e “sente” che qualcosa non va bene nel suo quadrato. Non gli resta che misurare i quattro lati (gli angoli erano già a posto) e rimane veramente sorpreso. Anche se di pochissimo (ma lui è molto sensibile), i lati BC e AC non sono lunghi come OA e OB. Impossibile, accidenti! Rifà le misure decine di volte, ma il risultato è sempre lo stesso: OACB non è un quadrato!

Altro che dormire… quel luogo dove è stato trasportato è sicuramente molto strano e deve scoprire perché. Beh… non sto a raccontarvi che prolungando le rette OA e BC, “parallele” per costruzione, le ha viste incontrare in un punto P e che, analogamente, le rette AC e OB si sono incontrate in Q (Fig. 14).

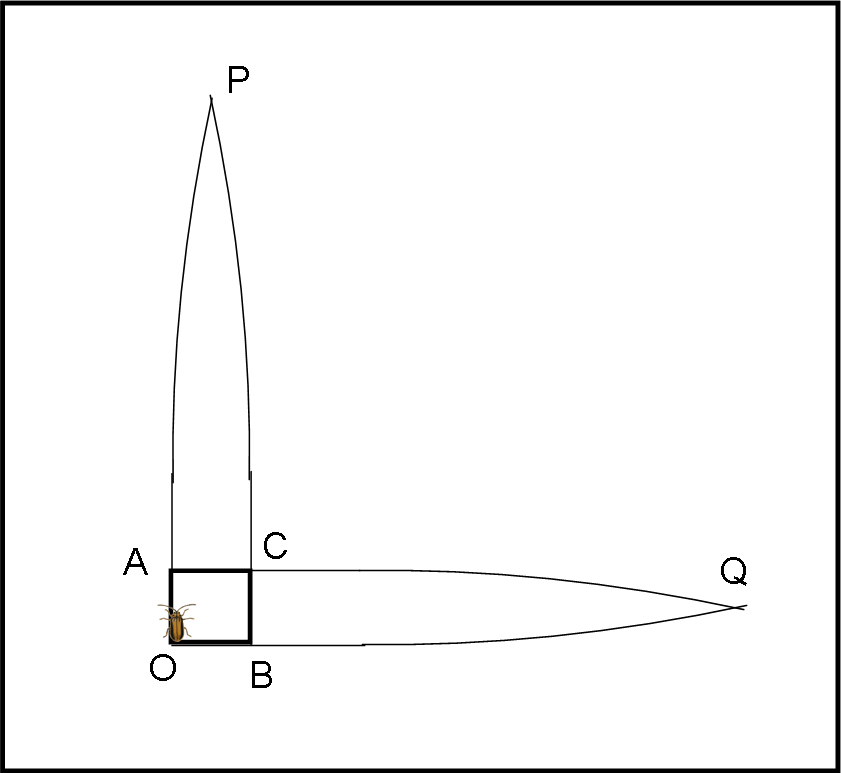
E nemmeno che è riuscito a costruire un triangolo con tre angoli retti (Fig. 15).

Insomma, il quinto postulato di Euclide e il teorema di Pitagora non valgono più! Il nostro bacherozzo, però, riesce abbastanza in fretta a comprendere come funzionano le cose in quello strano mondo a due dimensioni (andando a leggere questo articolo e probabilmente anche questo). E’ pronto a fare un esperimento decisamente interessante che serve non poco a proiettare e a immaginarsi al meglio una 2-sfera su un 2-spazio euclideo.

La Fig. 16 mostra il procedimento.

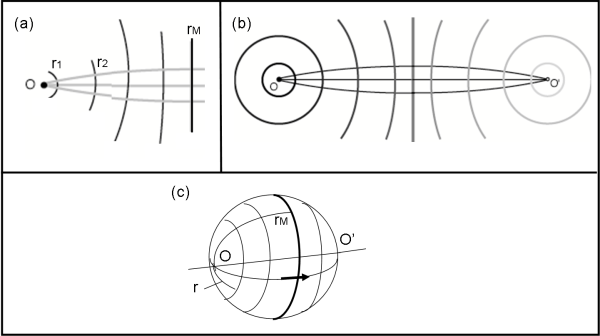
Inizia dal punto O e poi si sposta di r₁ lungo una retta e descrive una circonferenza di centro O e raggio r₁ (una 1-sfera). Continua ad aumentare il raggio, r₂, r₃, … fino a r_M . Senza grosse sorprese si accorge di descrivere circonferenze sempre più grandi. L’ultima coincide però con la retta perpendicolare a quella che sta seguendo (Fig. 16a). Un cerchio di raggio ben definito (l’ha misurato attentamente) che si trasforma in una retta?  Questo fatto succede normalmente quando il raggio è infinito… Ma adesso il bacherozzo è più che sicuro che il raggio sia finito e misurabile!

Boh… non gli resta che proseguire, allungando sempre più il raggio, che altro non è che la distanza da O al punto in cui è arrivato. Le cose sembrano tornare a funzionare e le circonferenze sono di nuovo realmente circonferenze. Però, però... gli sembra che invece di ingrandirsi, esse si stiano rimpicciolendo sempre più. Ne ha la certezza quando arriva nel punto O’. Le sue circonferenze sono terminate in un punto, che dista da O proprio il doppio di quello che distava da O il punto P trovato allungando due rette “parallele” (Fig. 16b). Il bello è che partendo da O’ e facendo lo stesso lavoro con le sue circonferenze di raggio crescente trova le stesse identiche configurazioni di prima e termina nel punto O di partenza. In Fig. 16c si vede bene cosa ha fatto il bacherozzo guardando il tutto dal 3-spazio che contiene la sua 2-sfera.

Il bacherozzo ha fatto un lavoro egregio e noi possiamo tornare al nostro progetto, ossia a quello di rappresentare una 2-sfera su un 2-spazio euclideo  (ossia un piano). Basta separare in due parti la nostra 2-sfera: da un lato mettiamo quella con centro in O e dall’altra quella con centro in O’., come mostra la Fig. 17. La circonferenza di raggio r_M è stata disegnata sia a sinistra che a destra (il suo raggio ha un valore finito).

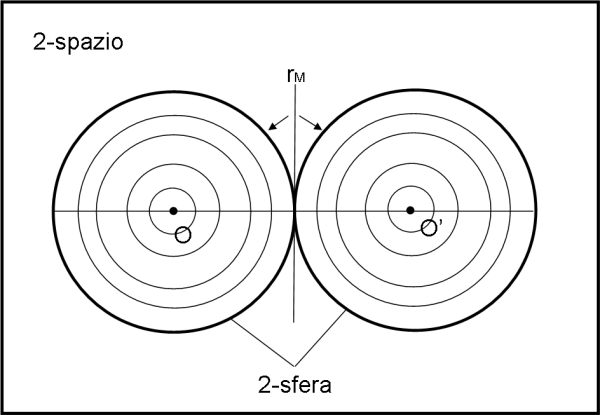
Due serie di tante 1-sfere concentriche, che si toccano in un solo punto. Tutta la 2-sfera è contenuta su di loro. Bene... siamo riusciti a “vedere” piuttosto bene (con un po’ di immaginazione e molta concentrazione) una 2-sfera in un 2-spazio euclideo. Qualcuno potrebbe dire: “Ma la 2-sfera è stata spezzata in due… non vale!”. “E perché no?”, diciamo noi, “Basta pensare (e il lavoro della mente ci vuole) che il cerchio massimo di destra vada a coincidere con il cerchio massimo di sinistra.

Questa rappresentazione è stata spesso usata nella storia della cartografia terrestre, come mostra la Fig. 18, che presenta un bellissimo planisfero del XVIII secolo.

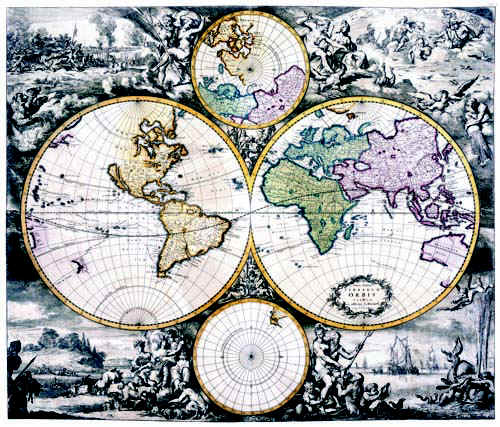
Su un 2-spazio euclideo è stata riportata perfettamente una 2-sfera non euclidea, rispettandone tutte le caratteristiche: rette (meridiani ed equatore) che si incontrano a 90°. Ma, soprattutto, le circonferenze che a partire da un polo aumentano per diventare una retta all’equatore e poi decrescere fino al polo sud, malgrado il raggio aumenti. La stessa figura poteva essere disegnata guardando il tutto dai due poli e il taglio della 2- sfera sarebbe coinciso con l’equatore. Nei due piccoli cerchi vicino ai poli della figura si applica questo procedimento, fermandosi molto prima dell’equatore, ma è facile comprendere la ovvia prosecuzione.

Sappiamo che esistono svariati sistemi di proiezione di una superficie sferica su un piano (proprio quello che interessa noi), ma quella che abbiamo scelto meglio si adatta per il passaggio successivo verso la 3-sfera.

Anzi, facciamo un passetto indietro e andiamo a recuperare una 1-sfera, che vogliamo rappresentare su un 1-spazio. Ormai dovremmo sapere come fare. Spezziamo in  due la 1-sfera e poi la rappresentiamo su due segmenti (1-spazio) che potrebbero essere incollati tra loro: di sopra ci sarebbe un emisfero e di sotto un altro; oppure uno di fianco all'altro. L’avremmo rappresentata su un 1-spazio euclideo, come mostra la Fig. 19.

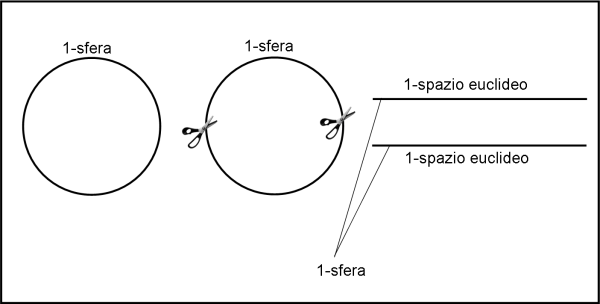
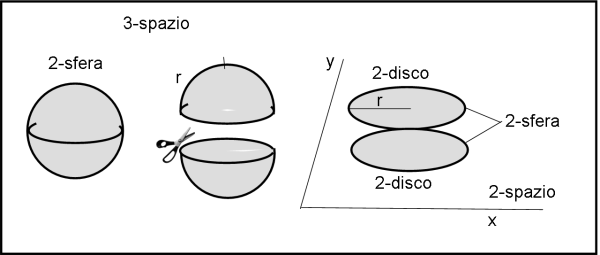
Non è un procedimento diverso da quanto abbiamo appena fatto con la 2-sfera…  Abbiamo preso la 2-sfera, l’abbiamo tagliata in due e poi l’abbiamo stesa su un 2-spazio euclideo. In pratica, abbiamo due 2-dischi circolari  in un 2-spazio euclideo, che corrispondono perfettamente alla 2-sfera di partenza. Potrebbero anche loro essere incollati assieme o , come presentato nel planisfero, messi a fianco, sapendo bene che arrivati in un punto al bordo del primo disco ci si sposta immediatamente sul punto equivalente del bordo del secondo: un apparente "salto di emisfero"!  Riportiamo nuovamente la manovra eseguita in Fig. 20 (sempre meglio ... abbondare...).

Esiste anche un’altra proiezione che trovo estremamente interessante per evidenziare al meglio un punto fondamentale a cui vogliamo arrivare con tutte queste discussioni sulla 2-sfera e tradurla sulla 3-sfera. Questa proiezione è quella usata nella bandiera dell’ONU e prende il nome di proiezione azimutale equivalente di Lambert. La costruzione è abbastanza semplice e la riportiamo in Fig. 21.

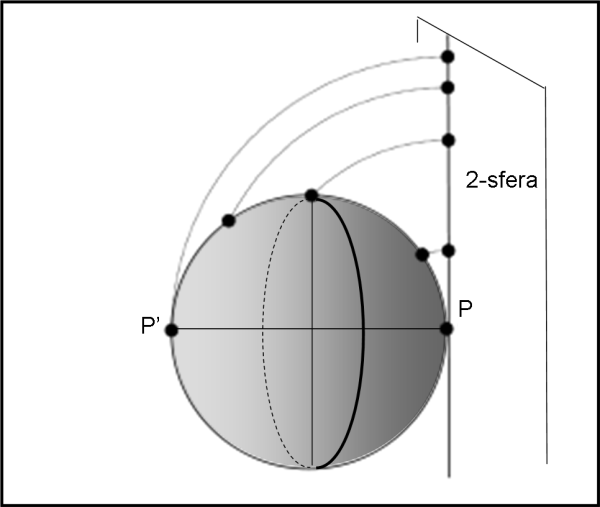
Si disegna un 2-spazio (piano) tangente alla 2-sfera terrestre in un suo punto per esempio il polo nord (P). E poi ogni altro punto della Terra viene riportato sul piano tangente  attraverso una circonferenza di raggio uguale alla distanza tra polo nord e punto scelto. Attenzione: se al posto di P ci fosse la Terra oggi e in P' ci fosse il Big Bang, non sembrerebbe  l'evoluzione dell'Universo?

In Fig. 22 vi è il risultato.

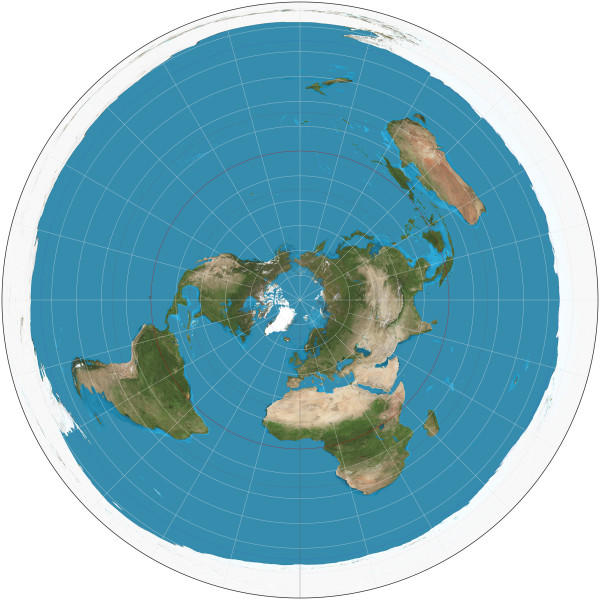
Si può vedere un fatto estremamente interessante per noi perché ci avvicina in modo impressionante al concetto di Big Bang e della sua visione  ovunque si guardi nel nostro 3-spazio. Il polo sud, ovviamente un punto, diventa una circonferenza che avvolge il mondo intero. Stranezze della proiezione? Sicuramente sì, ma quanta analogia con il Big Bang che è il punto dove tutto inizia e che però circonda sempre l’Universo in qualsiasi istante della sua vita! (Fig. 23)

Può essere utile riproporre in via ultra schematica l'Universo rappresentato in due dimensioni, ricordando che in realtà sono 4, e lo facciamo in Fig. 24

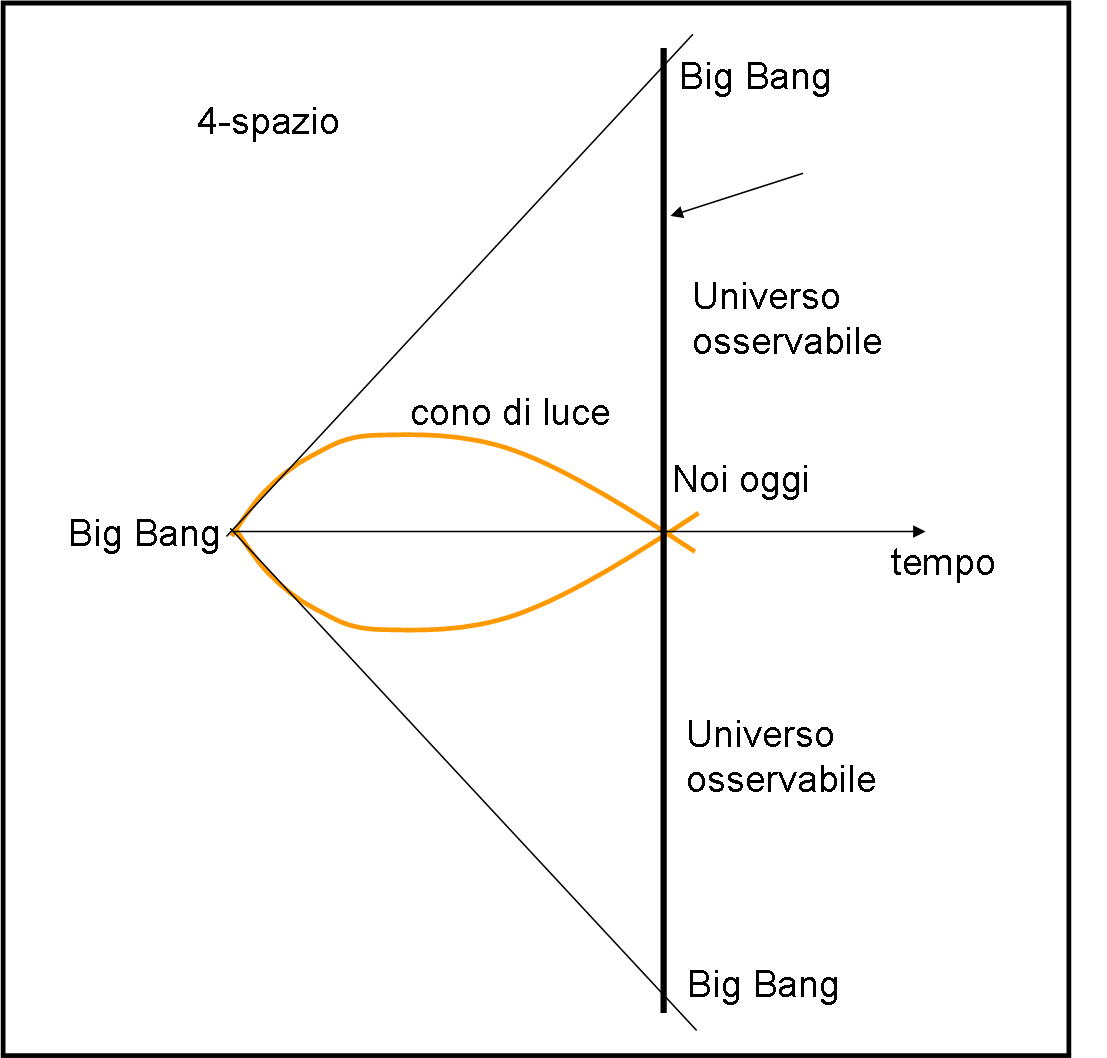
Comprendiamo subito che la Fig. 23 non è altro che l'Universo Osservabile della Fig. 24, esteso su due dimensioni. Il Big Bang, se si potesse vedere, sarebbe sempre ai bordi della 2-sfera finita e illimitata (il concetto di Universo osservabile e come e perché "vediamo" il Big Bang lo abbiamo spiegato QUI in modo approfondito).

Bene! Siamo finalmente pronti per il passaggio finale alla 3-sfera. In poche parole, ripetiamo rapidamente ciò che ha fatto Riemann e ciò che Einstein ha utilizzato per la sua teoria. Partendo da un punto locale (come abbiamo fatto per la 2-sfera) ci si è portati piano piano sempre più distanti svelando le caratteristiche di quello strano mondo non euclideo. Basta, perciò, aggiungere una dimensione in più e ripetere il percorso. Ovviamente, noi non lo faremo, ma l’analogia più semplice salta subito agli occhi e alla mente: se, a partire da un punto della 3-sfera, disegno delle 2-sfere con raggio crescente, a un certo punto mi troverò nelle condizioni di massima estensione, per poi iniziare a ritrovare sfere con raggio decrescente fino a giungere a un punto diametralmente opposto al primo.

Non è difficile "tagliare in due" questa misteriosa 3-sfera (che, ricordiamoci è immersa in un 4-spazio) e proiettarla direttamente in un 3-spazio (o addirittura in un 2-spazio sfruttando la nostra capacità di disegnatori…), come mostra la Fig. 25.

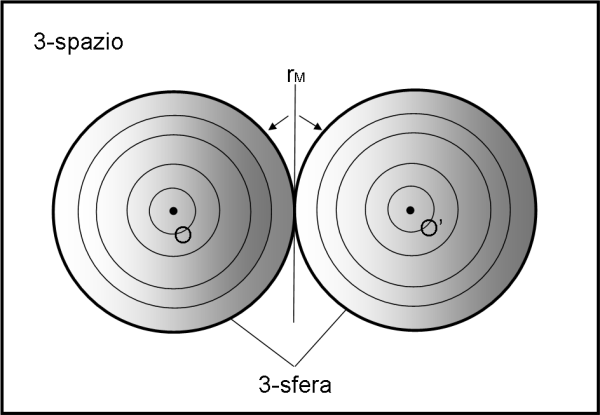
Anche se la figura lascia un po' a desiderare come ombreggiature, posso assicurarvi che essa mostra  due sistemi di sfere concentriche, del tutto uguali. Per ricostruire la 3-sfera “basterebbe” unire la sfera più grande di destra con quella più grande di sinistra. Cosa verrebbe fuori non è cosa per noi (aspettatevi tori e curve strane a non finire…), ma il concetto fondamentale che cercavamo rimane: spostandosi lungo una quarta dimensione del 4-spazio in cui è immersa la 3-sfera  ciò che sembrava un punto viene a circondare completamente le sfere iniziali (provate a immaginare di incollare la parte di destra sopra quella di sinistra facendo in modo che le due sfere maggiori si identifichino… ci vuole molta immaginazione, lo ammetto…). Ricordiamoci anche la proiezione delle Fig.re 21-24 ed estrapoliamole alle 3 dimensioni.

Questo è esattamente il modo in cui vediamo l’Universo oggi, per mezzo del telescopio: la 3-sfera che si trova alla distanza percorsa dalla luce dal momento del Big Bang, in realtà non è altro che l’immagine dispiegata di quel solo istante, come ci mostra la Fig. 26.

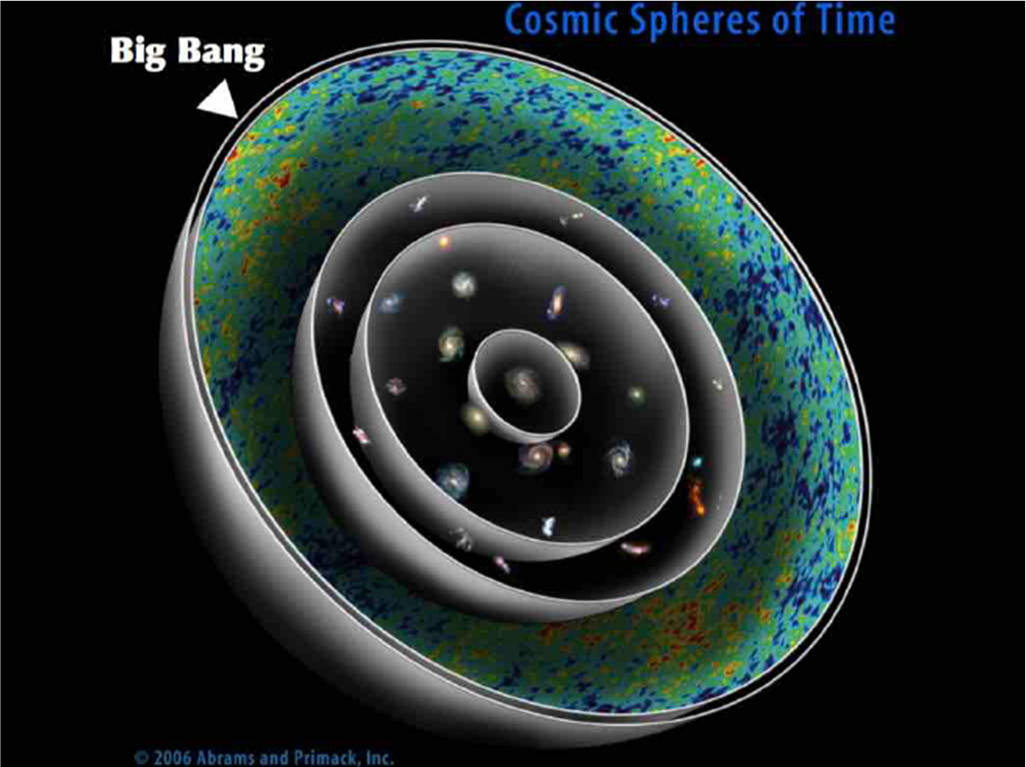
Abbiamo analizzato due modi per immaginarci la 3-sfera proiettata in un 3-spazio. Seguendo Flatlandia  siamo arrivati a una successione dinamica di sfere, dapprima crescenti e poi decrescenti. Imitando Riemann abbiamo ottenuto una doppia serie statica di sfere concentriche, di cui le due esterne sono in realtà coincidenti fra loro. La seconda è sicuramente preferibile e ci avvicina di più al nostro scopo finale.

Nell’Universo di Einstein questo è quello che capita prendendo il tempo come quarta dimensione: il Big Bang si vede dappertutto ed è la cosa più lontana visibile sempre e comunque. Un Universo finito e illimitato come la 3-sfera, ben lontano dall’Universo aristotelico dove non si accettava l’infinito e non si sapeva dove inserire Dio.  Aumentando infatti le sfere tolemaiche si sarebbe arrivati all'infinito aspettando sempre di dare un luogo alla residenza divina. Un 3-spazio infinito del tutto euclideo, ma assurdo sia teologicamente che scientificamente.

Se Einstein fosse vissuto ai tempi di Giordano Bruno non sarebbe scampato al rogo, anche se l’idea di Giordano Bruno era un Universo veramente infinito e con infiniti mondi. In un modo o nell’altro si sgretola la visione aristotelica. Tuttavia, c’è "qualcuno" che  dovrebbe essere probabilmente accusato di eresia profonda e che ha riportato le proprie idee senza paura di nasconderle. Troppo avanti per il suo tempo? Forse sì… è il destino dei più grandi geni.

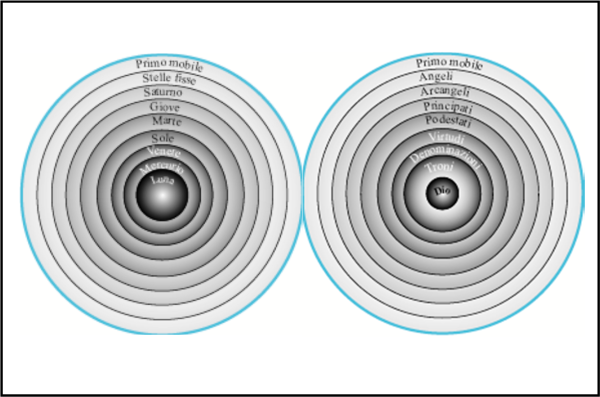
Non voglio dire altro, ma basti, per adesso, guardare la visione dantesca del mondo terrestre e dei vari cieli fino al primo mobile e poi la seconda parte dedicata al paradiso con le nove sfere che si rimpiccioliscono. No, la somiglianza con il modello di 3-sfera illimitata, ma finita, di Riemann  e  di Einstein non può essere un caso. Nessuno pretende certo di dire che Dante abbia risolto le equazioni di Riemann, ma solo che una mente geniale non poteva accettare l’assurdità aristotelica  di un Universo non infinito a sfere  sempre crescenti. L’unica soluzione era  immaginarsi un ipersfera a tre dimensioni. Un’illuminazione non voluta ma quasi obbligatoria per lasciare a Dio l’essenza di unica luce puntiforme, ma in grado di avvolgere l’Universo intero.

Fanno oggi ridere le figure quasi commoventi nella loro insensatezza che per secoli hanno rappresentato il viaggio di Dante (Fig. 27).

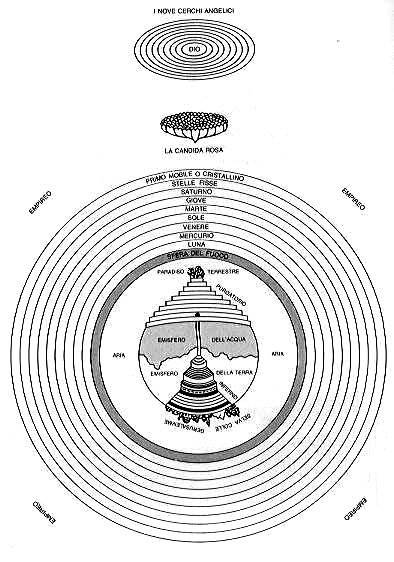
Un insieme di sfere concentriche e poi, giunti nell’Empireo, ecco comparire una struttura a nove sfere del tutto staccate e quasi insignificanti nella loro estraneità con il resto della costruzione pratica e teologica. Dante corregge Aristotele, imponendo quasi senza volerlo il concetto di 3-sfera, sicuramente inconscio, ma che dava l’unica soluzione possibile. Mostriamo l'Universo di Dante sotto questa visione in Fig. 28 e troveremo pari pari la Fig. 25.

Una illazione dei soliti scienziati che vogliono vedere il tutto dappertutto? Una creazione fantascientifica basata su casuali somiglianze tra l’Universo di Dante e quello di Einstein? Potrebbe anche essere, se la descrizione di questa visione sicuramente assurda per il suo tempo non fosse riportata più e più volte nella sua Commedia. Ovviamente, il poeta è uomo della Terra e come tale non può distinguere direttamente la 3-sfera (ne ha solo una visione confusa);  è costretto, allora, a guardarne il riflesso negli occhi di Beatrice, che fanno da filtro, mentre lei spiega quasi con sufficienza e con relativa pazienza l’intera costruzione.

Non ci rimane che fare il passo più importante che ci collega alla storia dei Catari, della loro visione dualistica, della nascita dell’eresia e degli stermini mostruosi perpetrati dalla chiesa. Una visione che ci ha portato fino a Dante per altra via. Uniamo adesso gli sforzi e andiamo a leggere la Divina Commedia con la dovuta attenzione. Einstein sarebbe d’accordo con noi…

Appendice

Per richiamare l'accurato e capillare lavoro di Arturo sopra i tori e le loro sezioni, dobbiamo accennare a un terzo metodo per visualizzare l’ipersfera a 3 dimensioni.

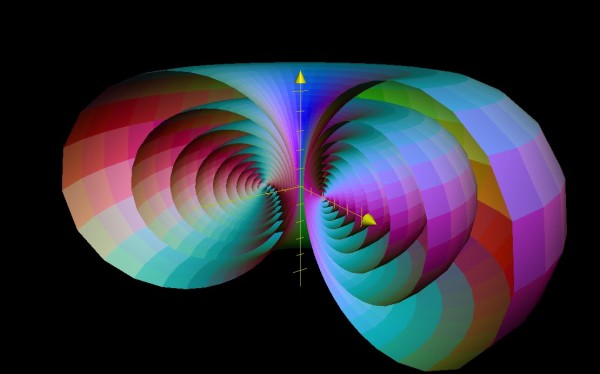
Nel 1931 Heinz Hopf scoprì che l’ipersfera si può considerare come una serie di cerchi massimi non intersecantisi e tutti inanellati fra loro. Questa rappresentazione oggi si chiama «fibrazione di Hopf», e, proiettata stereograficamente nello spazio tridimensionale, assume la forma del cosiddetto «toro di Clifford». Di seguito due rappresentazioni senza ulteriori commenti...

 

Chi volesse  saperne di più può andare QUI e QUI, ma a noi basta e avanza la doppia serie di sfere concentriche per entrare nel geniale Universo dantesco.