Categorie: Matematica Teoria degli insiemi
Tags: Riemann superfici Topologia
Scritto da: Umberto Cibien
Commenti:8
Superfici e varietà Topologiche.
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica
Un breve intermezzo prima della matematizzazione del nastro di MÖBIUS; il nastro è una superficie topologica ,che può avere delle determinate proprietà. Ma cos'è una superficie topologica? Quali sono queste proprietà ? Dobbiamo ancora definirle. Le definizioni introdotte non sono banali, e presuppongono la conoscenza degli articoli di topologia che trovate qui . Parleremo non solo di superfici ma anche di varietà; la definizione è la stessa, cambia solo la dimensione. La definizione di varietà che troverete in questo articolo è per così dire "autonoma", ed è fondata solo sulla Topologia.
Prima una ulteriore precisazione sugli spazi Topologici, la separazione:
Spazi di Hausdorff
Uno spazio topologico S è detto di Hausdorff se per ogni coppia x, y di elementi distinti di S esistono un intorno di x e un intorno di y disgiunti. In tal caso lo spazio si dice separato.
Come si può facilmente verificare, ogni spazio metrico è di Hausdorff. Non è però vero in generale per ogni spazio topologico.
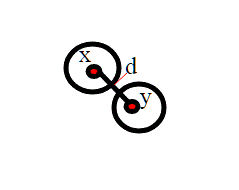
Noi tratteremo in questo conteso solo Spazi di Hausdorff.
Atlanti e carte geografiche
Lo studio topologico delle superfici deriva sostanzialmente dalla geografia.
La sfera (schematizzazione della superficie terrestre) può essere rappresentata sul piano tramite un atlante di carte

geografiche; Purtroppo non è possibile usare solo una carta(ovvero un solo omeomorifismo), perchè la sfera non è omeomorfa ad un piano. Localmente invece, si trovano degli aperti sulla sfera che lo sono. Le funzioni che trasformano gli aperti della sfera in aperti del piano sono degli omeomorfismi che però non conservano le distanze; le carte permettono di introdurre coordinate locali (nel caso specifico la longitudine e la latitudine). Infatti l'immagine di un punto della sfera è un punto nel piano, dove esistono le coordinate (x,y).

Possiamo pensare alla sfera (terra) come ad un puzzle tridimensionale. Tutti gli elementi che lo compongono ricoprono interamente al sfera e una volta "stirati" con un omeomorfismo formano un insieme di carte geografiche, ovvero un atlante. Noi che viviamo sulla superficie della terra, sperimentiamo direttamente ogni giorno che"localmente" la superficie della terra assomiglia ad un piano euclideo.
Spazi topologici localmente euclidei.
è un particolare spazio topologico, ed altro non è che lo spazio Euclideo, munito di coordinate. In esso abbiamo la distanza pitagorica, quindi possiamo definire gli aperti chiamati bolle :
{
tali che
}.
Le abbiamo viste negli spazi metrici. Un aperto particolarmente semplice, è il disco di raggio unitario con centro nell'origine, che chiamiamo .
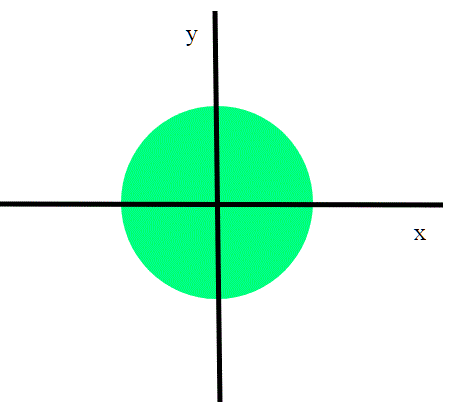
Uno spazio topologico X si dice localmente euclideo se ogni suo punto x ha un intorno aperto Ui omeomorfo a un disco aperto in
(o equivalentemente a tutto
). Chiamiamo
;
La coppia ( ,
) si chiamo carta locale.
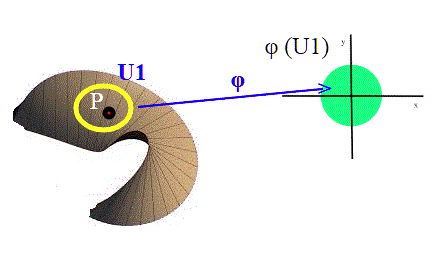
Non fatevi spaventare dai formalismi e dagli indici; come nella figura prendiamo un punto P qualsiasi; se lo spazio è localmente euclideo esiste un intorno aperto U e una applicazione continua e invertibile (omeomorfismo) tale che la sua immagine
(U) sia un aperto di
.
Uno spazio topologico connesso (fatto di un solo pezzo), di Hausdorff, e localmente euclideo si dice varietà topologica.
Chiaramente adesso salta fuori il discorso sulla dimensione di tale varietà, che è proprio l'n di .
Tramite un omeomorfismo una curva va in una curva, una superficie va in una superficie, un solido va in un solido, infatti si conserva la dimensione (le curve, le superficie, i solidi hanno rispettivamente dimensione uguale a 1; 2; 3);
Se n=2, abbiamo una varietà topologica di dimensione due, che è detta superficie topologica.
E' da notare che queste varietà introdotte solo così, dal punto di vista topologico, non richiedono nessuna immersione in nessun spazio. Sono , per così dire ,autonome.
Ricoprimenti e atlanti in topologia.
Restiamo per ora nell'ambito delle superfici.
In generale, chiamiamo ricoprimento di uno spazio topologico S,una famiglia di insiemi tali che
, ovvero la loro unione dà tutto S .
Sia allora una superficie. Se per ogni
esiste un omeomorfismo
:
dove , allora siamo in grado di trasformare un aperto della topologia di S in un disco del piano. Come già detto, la coppia (
,
) si chiamo carta e l'insieme di tutte le carte
si chiama atlante.
Quindi ogni superficie ammette un atlante.
(possiamo estendere questa definizione di atlante alle varietà n-dimensionali, sostituendo a
).
Spazi Compatti.
Parliamo di spazi, perchè la compattezza è un concetto che non riguarda solo le superfici. Nell'esempio citato delle mappe e degli atlanti, sappiamo che per costruire un atlante della terra bastano un numero finito di mappe. Quindi la superficie della terra, come quella della sfera, è finita. Dato uno spazio topologico S,per dire se è compatto dobbiamo verificare , per ogni una famiglia di aperti Ui tale che la loro unione dia S, se questo riusciamo a realizzarlo con un numero finito di questi aperti. Dunque uno spazio topologico è compatto se ammette un sottoricoprimento finito, per ogni ricoprimento aperto.
Gli esempi più noti di spazi compatti sono la sfera e il toro.
Superfici con bordo
Negli spazi è relativamente facile definire il bordo di un semispazio. Pensiamo ad esempio al bordo di un tavolo.
Consideriamo il semipiano di definito da:

in pratica la zona in verde unita alla linea rossa. Chiamiamo bordo del semipiano la retta (rossa) di equazione:
y=0
Tale bordo viene indicato con . Definire il bordo in
ci permette, tramite gli omeomorfismi , di definire i bordi in una superficie qualsiasi.
Definiamo allora le superfici topologiche con bordo; intuitivamente, una superficie con bordo assomiglia (cioè è localmente omeomorfa) ad un disco o ad un semidisco; i punti di M che hanno intorni che somigliano (cioè sono omeomorfi) ad un semidisco costituiscono il bordo della superficie. Gli altri punti sono detti punti interni. I punti del bordo sono" intrinsecamente" differenti dai punti della superficie S privata del bordo
. Se il bordo di una superficie è vuoto, (
), la superficie è senza bordo.

In una superficie abbiamo a disposizione un altante; esistono perciò degli omeomorfismi definiti su ogni aperto che contiene ogni punto della superficie; i punti P per cui
appartiene al bordo
sono i punti del bordo
di S. Se
la superficie si dice senza bordo. Anche i bordi sono delle varietà ; in questo caso ogni punto del bordo è omeomorfo alla retta y=0, ed ha dimensione n-1, ovvero 2-1=1(è una curva). Una sfera non ha bordo, mentre il cilindro ne ha due, e sono le due circonferenze di base. Il toro non ha bordi.
 |
 |
 |
NB. La definizione di bordo può essere estesa alle varietà qualsiasi, di dimensione n. Basta sostituire al semipiano il semispazio
, e come bordo
l' iperpiano di equazione
. Dopodichè, si considera l'immagine del bordo tramite gli omemomorfismi che definiscono la superficie.
Spazi semplicemente connessi.
Uno spazio topologico si dice semplicemente connesso se è connesso per archi e ogni curva chiusa giacente su di esso può essere deformata fino a ridursi a un singolo punto (appartenente sempre alla superficie).
Intuitivamente uno spazio è semplicemente connesso quando è privo di "buchi". Dunque, ad esempio, la sfera risulta essere semplicemente connessa,mentre il toro non è semplicemente connesso.


Superfici orientabili e non orientabili
Riprendiamo in mano il nostro cilindro con due bordi. Intuitivamente non facciamo nessuna fatica a pensare che il cilindro abbia un "dentro" e un "fuori" ovvero due facce.

E' possibile colorare la superficie del cilindro con due colori diversi, uno per la parte esterna e uno per la parte interna. Si dice in questo caso che la superficie del cilindro è orientabile. Questa è la definizione "antica" di superficie orientabile. In pratica non è possibile passare da una faccia all'altra senza attraversare il bordo o bucando la superficie. Nel quiz art-attak di Maurizio abbiamo già visto un esempio di superficie non orientabile, che è proprio il nastro di MÖBIUS; nell' esempio reale del quiz abbiamo toccato con mano l'impossibilità di colorare il nastro con due colori diversi, infatti se proviamo a colorare il nastro partendo da un suo punto qualsiasi, finiamo con il colorare tutto il nastro senza attraversare il bordo.
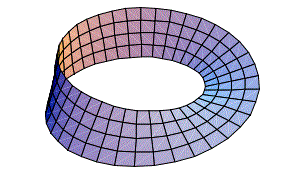
A questo punto, i matematici dicono semplicemente: una superficie non è orientabile se e solo se contiene un nastro di MÖBIUS . Questa è una definizione moderna di orientabilità.
Nel prossimo articolo vedremo in dettaglio la costruzione di queste due superfici (cilindro e nastro) usando la topologia quoziente.






8 commenti
Una domanda sulla definizione di spazio localmente Euclideo.
La superficie di una sfera è uno spazio localmente Euclideo?
Dalla definizione mi sembrerebbe non lo sia. Dato un punto P qualsiasi della sfera non mi sembra ci sia un intorno sulla sfera che contenga il punto e sia Euclideo. Ovviamente esiste il piano tangente che è Euclideo, ma questo ha il solo punto P in comune con la sfera.
E’ sufficiente per soddisfare la condizione?
Il dubbio viene dal fatto che in altre occasioni ho visto portare la superficie della sfera proprio come primo esempio di varietà non Euclidea con, più o meno esplicitamente, evidenziata la proprietà di essere localmente Euclidea.
Colgo l’occasione per ringraziare Umberto per il lavoro che sta facendo per accompagnarci nella esplorazione di questi campi della matematica. Certamente sono articoli che richiedono un livello di attenzione elevato, almeno per me. Non lo dico come un difetto, tutt'altro. La cosa “divertente” è proprio affrontare questa complessità con una opportuna guida.
scusa per gli errori di scrittura ma sono con il cellullare. In ogni caso parliamo di omemorfismi topologici, non di metrica.
in modo molto semplificato, rifacendomi all'approccio di Riemann, ogni superficie può essere considerata localmente euclidea. Pensa a una cartina topografica. Le differenze fondamentali si troveranno a poco a poco andando verso una visione globale, un po' come ha fatto lo scarafaggio nell'articolo sulla ipersfera. Mi lancio in un paragone azzardato: anche la RG può essere considerata un approccio in cui si inizia con la RR e si stabiliscono poi differenze minime tra successivi sistemi inerziali...
Ovviamente è una visione rozza e primitiva... niente a che vedere con la rigorosità di Umberto
però è proprio così. Ho fatto sempre confusione anch'io a comprendere a fondo la differenza fra locale e globale, soprattutto quando si parla di RG.Non si capisce bene dove ci troviamo.
Probabilmente il mio errore è proprio partire da quanto dice Enzo, che è sostanzialmente quello a cui facevo riferimento quando parlavo di piano tangente. In effetti è vero che riducendo l'interno del punto P sulla sfera l'errore che si fa rispetto ad un piano Euclideo è sempre minore, ma un errore per quanto piccolo rimane. Ad esempio, se prendo come coordinate due cerchi massimi ortoganali passanti per il punto e non allontanandomi troppo dal punto posso dire che un buona approssimazione delle distanza è quella Euclidea, ma è pur sempre una approssimazione, per quanto buona o buonissima. Quindi non posso assimilare l'intorno ad un piano se non al limite di un intorno infinitesimo, ma nelle considerazioni di Umberto mi sembra non ci sia ancora una definizione di infinitesimo. Comunque non saprei dire in un intorno infinitesimo se ci sono altri punti oltre a P stesso.
Mi sembra che Umberto dica che tutto questo non è necessario per definire il punto come "localmente Euclideo", ma occorre solo che ci sia un omeomorfismo con il piano Euclideo. Per vedere se ho capito provo a direlo in forma non rigorosa interpretando quello che Umberto scrive come definizione di omeomorfismo nella parte 3a.
L'importante è che si possa mappare ciscun punto dell'intorno del punto P in un punto del piano Euclideo in modo biunivoco (senza considerare le proprietà relative alla distanza che afferiscono alla metrica). Sulla sfera questo effettivamente si può fare e non è neanche necessario mantenersi nelle vicinanze del punto P.
come al solito le tue considerazioni , Fabrizio, vanno a centrare il problema. Domani cercherò di chiarire i dubbi emersi. Per ora posso solo dirti che la definizione topologica di varietà che ho dato é quella base. Le altre, come dicevi, fanno uso della differenziabilità, e della metrica. Ancora non le abbiamo affrontate. Lo faremo? Non lo so. Comunque mi fa molto piacere discuterne.
Fabrizio scrive, per dare la definizione di localmente euclideo:
"L'importante è che si possa mappare ciascun punto dell'intorno del punto P in un punto del piano Euclideo in modo biunivoco (senza considerare le proprietà relative alla distanza che afferiscono alla metrica). Sulla sfera questo effettivamente si può fare e non è neanche necessario mantenersi nelle vicinanze del punto P."
E va bene. Aggiungo che io non parlerei proprio di distanza;negli spazi topologici abbiamo gli aperti e gli omeomorfismi, ma non la distanza. Gli omeomorfismi non è nemmeno detto che siano differenziabili. V è infatti uno spazio topologico, non è strutturato per poter parlare di derivazione. E, ripeto, negli spazi topologici può non esistere la distanza.
Se prendiamo come esempio ancora la sfera, non possiamo ricoprirla con un unico omeomorfismo, perchè ci sono di mezzo i poli, ma con due si . Basta prendere due semisfere è proiettarle ottenendo due dischi, deformandole con degli omeomorfismi. Otteniamo così un atlante. Lo scopo di questa definizione topologica di varietà è questa. Non bisogna confonderla con altre o cercare di anticipare le varietà Riemmane, in cui esiste una metrica.La definizione di superficie topologica, dice solo che è possibile portare (a pezzetti) tale superficie su un piano, creando un atlante Questo inoltre, definisce la vera dimensione della varietà. Nel caso di superficie, parlando di omemomorfismi con il piano, la dimensione è 2.