Questo articolo fa parte della serie dedicata alla Relatività di Epstein, all'interno della sezione d'archivio  "Relatività Ristretta"

 

Questo strano quiz-non quiz permette di introdurre un sistema estremamente semplice e immediato per riassumere le maggiori conseguenze della relatività speciale. Un sistema che teoricamente (ma anche praticamente) permette di non usare assolutamente il diagramma di Minkowski e la sua geometria iperbolica. Tuttavia, ho reputato interessante il suo uso e la sua descrizione solo dopo aver compreso profondamente i principi della relatività ristretta nel modo più completo e appropriato. In altre parole, chi già sa può anche permettersi questo “lusso”. Resta il fatto che dilatazione dei tempi e la contrazione delle lunghezze diventano graficamente un gioco da bambini

La domanda che vi faccio è piuttosto semplice... "Perché non si può superare la velocità della luce?" Ci sono tanti modi per rispondere, più o meno validi e più o meno fisici. Li conoscete sicuramente molto bene e potete anche rispondere. Tuttavia, ve ne voglio proporre uno un po' "eretico".

La risposta suona abbastanza  strana: Niente può superare la velocità della luce solo perché niente può andare più piano della velocità della luce! Infatti, qualsiasi cosa (compresi voi) va sempre e comunque alla velocità della luce! chiedete ai fotoni se non ci credete… Ti senti immobile, seduto sulla tua poltrona? Illuso… ti stai muovendo alla velocità della luce attraverso il tempo!

Velocità temporale e velocità spaziale

Ogni persona o cosa definisce la direzione del proprio movimento come asse del tempo (in pratica, il tempo proprio). Le tre direzioni ad esso perpendicolari vengono chiamate spazio.

Se uno è fermo, tutta la sua velocità è utilizzata per muoversi attraverso il tempo, dal passato al futuro. Quando, invece, ci si comincia a muovere spazialmente, una parte di questa velocità viene utilizzata per spostarsi nello spazio. Facendo questo, però, si cambia sistema di riferimento e quindi anche la nuova direzione del moto. Lungo quest’ultima direzione ci si continua a muovere con velocità uguale a c.

Capiamolo meglio con la Fig. 1, dove abbiamo indicato solo l’asse spaziale x e l’abbiamo chiamato s, dato che è la direzione dello spostamento spaziale. Sappiamo, comunque, che esistono anche gli assi spaziali y e z ad esso perpendicolari, che non ci interessano assolutamente.

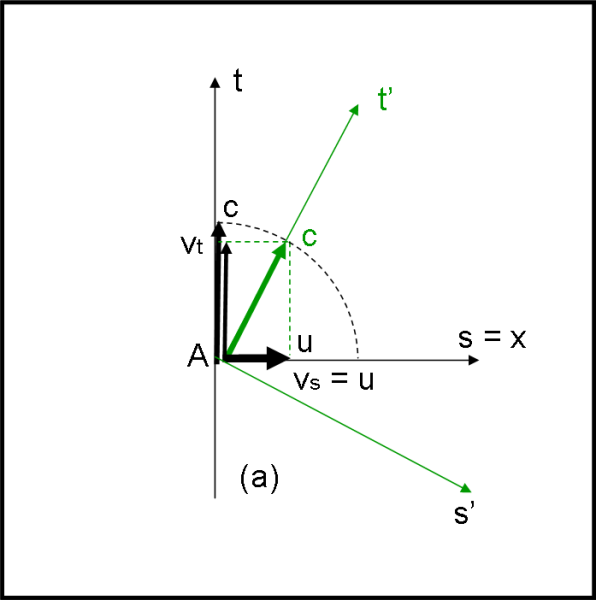
Noi stiamo viaggiando lungo l’asse t (verticalmente), ma, giunti in A, decidiamo di accendere un motore e di muoverci anche nello spazio s con una velocità spaziale u.  Accendendo il motore la direzione del moto cambia ed essa diventa il nostro nuovo tempo (verde) che si porta dietro il proprio spazio, perpendicolare a questa nuova direzione. Rimaniamo sempre in uno spaziotempo a quattro dimensioni (abbiamo cambiato solo il nostro sistema di riferimento) e la velocità è sempre c. Praticamente è come se la nuova velocità della luce si dividesse nelle sue due componenti v_t e v_s = u, rispetto al vecchio sistema di riferimento, quello antecedente all’accensione del motore (nero).

Non è nemmeno difficile utilizzare unità di misura equivalenti nel tempo e nello spazio: nel tempo la velocità si misura in secondi al secondo e nello spazio in secondi luce al secondo. E’ un discorso che, in fondo, conosciamo già (QUI, capitolo “qualche piccola modifica”): per uguagliare l’unità di misura del tempo e dello spazio abbiamo moltiplicato il tempo per la velocità della luce. In tal modo un secondo sull’asse dei tempi equivale a una distanza in secondi luce, proprio come viene misurato lo spazio.

Come al solito, ovviamente, chi comanda il gioco è il sistema di riferimento. Potrei, infatti, fare questa affermazione: “Esiste sicuramente un sistema di riferimento secondo il quale noi stiamo andando alla velocità della luce. Basta interrogare un fotone e chiedergli a che velocità stiamo andando. La sua risposta sarebbe proprio in linea con la nostra affermazione. Non solo… Se gli chiedessimo come sta girando il nostro orologio, ci direbbe che gli sembra rotto… dato che non si muove assolutamente. In altre parole, la componente della velocità temporale sarebbe zero (il tempo non passa) e quella spaziale sarebbe massima (percorriamo 300 000 chilometri al secondo)”.

Altro che crescita di massa, energia infinita, e tutta quella fisica complicata. Basta un semplice grafico e una visione puramente geometrica…

Prima di procedere, stiamo attenti a non confondere un metodo di descrizione estremamente utile, sia qualitativamente che quantitativamente, con delle verità fisiche (ecco perché preferisco che si affronti solo dopo aver digerito la teoria fisica della relatività ristretta). Ovviamente, non sono stato io a scoprire questo sistema decisamente geniale e semplice (si possono avere risultati immediati e con ottima approssimazione con solo un foglio di carta quadrettata e senza alcuna formula), ma Lewis Carroll Epstein, all’inizio degli anni ’80. Snobbato dai più, forse a causa della quasi ridicola facilità di ottenere le conclusioni di Einstein (visto il nome molto simile, non è che sia lo stesso Einstein redivivo che si è divertito con la sua stessa teoria?), rimane comunque un approccio degno della massima attenzione. La sua descrizione ammette chiaramente che può essere pensato solo dopo che Einstein ha definito fisicamente la relatività ristretta, attraverso i suoi postulati. Una semplificazione a posteriori, che mai si sarebbe ottenuta senza sapere il risultato.

Vediamo, allora, di divertirci e descrivere le parti più interessanti… ricordando che tutto ciò che bisogna conoscere è un briciolo di trigonometria e saper tracciare delle perpendicolari..

Due sistemi di riferimento

Dimostreremo, con diagrammi semplicissimi, che tutti i fenomeni descritti dalla RR derivano dal fatto che, pur muovendoci tutti alla velocità della luce, non lo facciamo nella stessa direzione nello spaziotempo a quattro dimensioni. Ribadiamo ancora che un  secondo di tempo corrisponde a 300 000 km.

In realtà, non abbiamo affatto bisogno di usare tre assi spaziali: ne basta uno solo, quello in cui un sistema si muove relativamente ad un altro. Le altre due direzioni non comportano alcun effetto. Il nostro spaziotempo è quindi  disegnabile su un foglio quadrettato, in cui si possono facilmente rappresentare e confrontare i due sistemi di riferimento. L’importante è che entrambi si trascinino dietro un asse perpendicolare a quello del tempo.

La Fig. 2 mostra un sistema di riferimento (a), ad esempio il nostro. Noi siamo la persona A che si muova alla velocità della luce lungo l’asse t. Noi ci sentiamo, comunque, sempre fermi nello spazio!

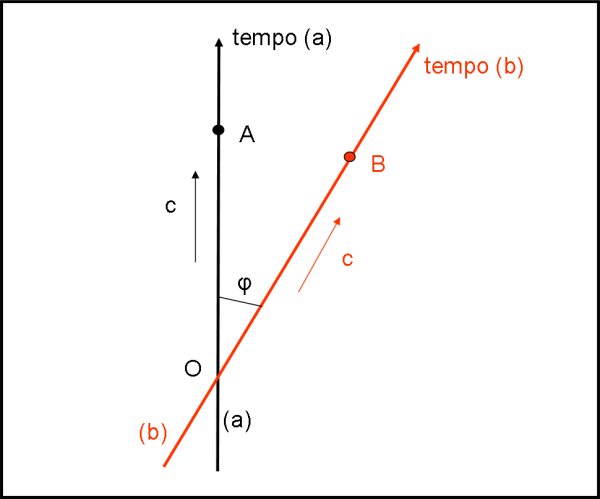
Inseriamo un altro viaggiatore B, il quale, ricordiamolo bene, viaggia nel suo tempo che è un asse diverso dal nostro (sistema (b)). Inseriamolo come linea rossa. Ammettiamo che i due viaggiatori (A e B) si incontrino, per la prima volta, in O. A quel punto azzerano i propri orologi che, comunque, scandiscono lo stesso tempo (il tempo proprio).

Dopo un certo periodo di tempo, A e B si trovano nelle rispettive posizioni indicate in figura e, per definizione, OA = OB (viaggiano alla stessa velocità…). E’ importante introdurre l’angolo φ tra le loro direzioni. E ancora più importante stabilire che quest’angolo non può mai essere maggiore di 90°. Se così fosse il viaggiatore B potrebbe muoversi nel suo spazio (accendendo un motore, per esempio) e intersecare il nostro asse del tempo PRIMA che si sia verificato l’evento O e questo non può essere accettato: nessuno può influire sul nostro passato.

Diventa ovvio tracciare la circonferenza di centro O e raggio OA = OB. Essa definisce la posizione di ogni viaggiatore nel suo sistema di riferimento dopo che si è incontrato con noi nel punto O ed è passato un certo periodo di tempo, che è uguale per ogni sistema.

Abbiamo tutti i mezzi (estremamente banali) per analizzare il moto di B nel sistema di riferimento (a). Tracciamo in Fig. 3 la perpendicolare da B all’asse spaziale di (a) e scriviamo alcune formule di una semplicità sconcertante.

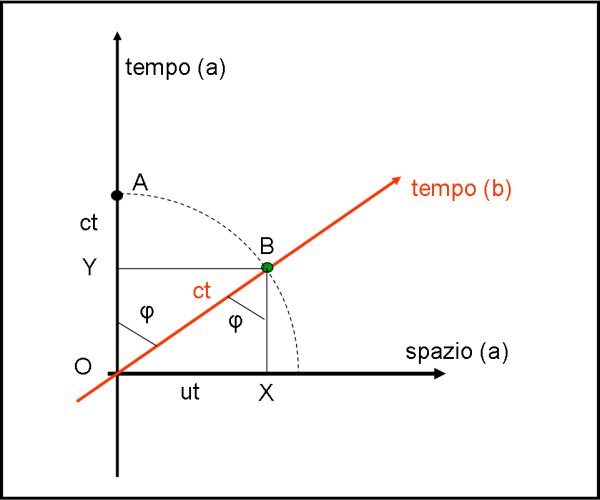
Il sistema (a) descrive il moto di B nel seguente modo: nel tempo che io ho impiegato a percorrere il tratto temporale OA, il viaggiatore B ha percorso uno spazio OX. In altre parole, l’osservatore A ha visto MUOVERE nel suo spazio il viaggiatore B con una certa velocità u. In realtà, però, come ormai sappiamo bene, B si muove  alla velocità della luce lungo il suo asse (rosso) temporale. Ancora una volta, la velocità appare diversa se misurata da un sistema di riferimento diverso.

OX/OB = OX/OA = sen φ

Nient’altro che un’applicazione dei rudimenti della trigonometria…

Per quanto imposto fin dall’inizio sulle unità di misura, sappiamo che OA = OB = ct   OX = ut, per cui:

u/c = sen φ                       …. (1)

Utilizzando la (1) e ricordando che (sen²φ + cos²φ) = 1,  possiamo anche scrivere

√(1 – u²/c²) = √(1 – (u/c)²) = √(1 – sen²φ) = cos φ                      ... (2)

Le due relazioni ci permettono, mettendoci in (a), di proiettare OB secondo il suo spazio s e il suo tempo t.

Dilatazione del tempo

Ricominciamo dall’inizio e descriviamo con estrema semplicità ciò che accade. A e B si incontrano in O e mettono a zero i propri orologi, senza ovviamente fermarsi. Ognuno prosegue per la sua strada fino ai valori riportati in figura.

I due orologi segnano lo stesso tempo e possiamo scrivere che:

OA = OB = ct       (dove t è il tempo trascorso dall’incontro in O, uguale per entrambi)

Ne segue che

OX = OB sen φ

OX = ct · (u/c) = ut 

Come già avevamo dedotto.

Più interessante ancora è la proiezione di OB su OA.

OY = OA cos φ = OA √(1 – u²/c²)     …. (3)

Cosa ci dice questa relazione? Banale…

OA è il tempo trascorso secondo l’orologio di A, mentre OY è il tempo trascorso dall’orologio di B secondo il punto di vista del sistema (a).

Il sistema (a) misura direttamente sul suo asse temporale il tempo passato per B. Esso risulta decisamente più corto di OA e, quindi, ad (a) sembra che il tempo di (b) scorra più lentamente del suo. Questo ragionamento vale per qualsiasi angolo acuto φ e, perciò, una semplice proiezione grafica ci permette di calcolare la dilatazione dei tempi di qualsiasi oggetto in moto relativo rispetto ad (a).

In poche parole, OY rappresenta il tempo t’, ossia quello trascorso in (b) secondo (a), mentre OA rappresenta il tempo t proprio del sistema (a).

La (3) diventa la ben nota formula einsteiniana della dilatazione dei tempi in cui γ  = 1/√(1 – u²/c²) è il celebre fattore di Lorentz.

t’ =  t √(1 – u²/c²) = t/γ

Un gioco alla portata di chiunque…

Notiamo anche che si ottengono facilmente i casi limite. Se il sistema (b) non si muove assolutamente, ossia si comporta come (a), possiamo dire che le componente della sua velocità lungo s è zero e che tutta la velocità è temporale, ossia vale c (un secondo al secondo). Se invece (b) si muove rispetto ad (a) alla velocità massima possibile (ossia c), tutta la sua velocità è lungo s e ciò vuol dire che, per (a), il sistema (b) viaggia alla massima velocità spaziale senza che il tempo passi. E’ proprio quello che sappiamo riguardo al fotone: il suo orologio non gira, se visto da (a), ma esso viaggia alla massima velocità possibile.

Ovviamente, si mantiene una perfetta simmetria su ciò che vedono i due sistemi (a) e (b), come mostrato in Fig. 4.

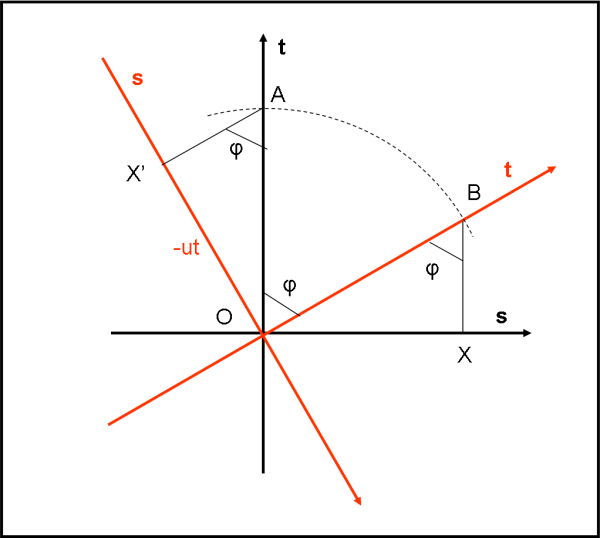
Mettiamoci, infatti nel sistema di (b) e disegniamo come lui vede il movimento di A. Se prima il moto di B si proiettava su OX, adesso è il moto di A che si proietta su OX’. Tuttavia, i due triangoli OBX e OAX’ sono uguali (o congruenti, come preferite). Tutto è assolutamente simmetrico rispetto a ciò che vede (a), a parte il fatto che la velocità diventa –u.

Fermiamoci qui, ma possiamo già capire come ottenere anche la contrazione delle lunghezze… provateci voi, in attesa della prossima puntata…